תמורות ושילובים בתורת הצירופים

האופנים לסידור פריטים כוללים:

• תמורה פרמוטציה כשהסדר חשוב.
• שילוב קומבינציה כשהסדר לא חשוב.

תמורות (פרמוטציות)

תמורה (פרמוטציה) היא מספר הדרכים לסידור פריטים כשהסדר חשוב.

לדוגמה, אם עומדות לרשותנו האותיות A ו-B בלבד ניתן לסדר אותם בשני אופנים כאשר הסדר חשוב:

A B
B A

• 2 אופני סידור = 2 תמורות (פרמוטציות)

אם עומדות לרשותנו האותיות A, B, C אז ניתן לסדר אותם ב-6 אופנים שונים:

A B C
A C B
B A C
B C A
C A B
C B A

• 6 אופנים לסדר 3 פריטים = 6 תמורות (פרמוטציות)

את מספר הפרמוטציות מוצאים באמצעות עצרת!

לדוגמה, כמה דרכים שונות קיימות לסידור 4 פריטים? התשובה היא 4 עצרת:

4! = 4 * 3 * 2 * 1 = 24

• בשביל לחשב עצרת לוקחים את המספר 4 וכופלים אותו בכל המספרים הקטנים ממנו עד שמגיעים ל-1.

לדוגמה n עצרת:

n! = n * (n-1) * (n-2) * … * 1

• מכפלת כל המספרים השלמים מ-1 עד n כולל.

לדוגמה, 2 עצרת:

2! = 2 * 1 = 2

• כאשר 2 הוא מספר התמורות בהם ניתן לסדר 2 פריטים.

לדוגמה, 3 עצרת:

3! = 3 * 2 * 1 = 6

• כאשר 6 הוא מספר התמורות בהם ניתן לסדר 3 פריטים.

עוד דרך להסתכל על זה היא שיש 3 אפשרויות סידור עבור המקום הראשון, 2 עבור השני, ומה שנשאר זה רק 1 עבור המקום השלישי:

3 * 2 * 1 = 6

• עבור האות הראשונה יש 3 אפשרויות, עבור האות השנייה רק 2, ועבור האות השלישית נותרת אפשרות 1.

נוח להבין את זה אם משתמשים בדיאגרמת עץ:

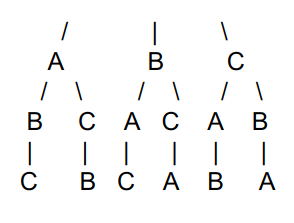
• כשעוברים לאורך הענפים מלמעלה למטה רואים 6 ענפים כמספר האפשרויות שגם הוא 6.

נסכם, !n (עצרת) משמש לחישוב מספר כל התמורות (כל אפשרויות הסידור) של n פריטים. לדוגמה, סידור 3 פריטים.

בוא נסבך את זה אבל רק קצת.

כמה תמורות (פרמוטציות) נדרשות לסידור מילים בנות 2 אותיות מתוך 3 אותיות?

אפשר לכתוב את זה כך:

nPr

• איך קוראים את זה? מתוך n פריטים בחר r.

לדוגמה, מתוך 3 אפשרויות בחר 2:

3P2

וכל זה היה הכנה להצגת הנוסחה לחישוב מספר הפרמוטציות:

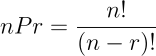
נציב בנוסחה את n מספר הפריטים הכולל (3) ואת r מספר הפריטים המבוקש (2), ונקבל:

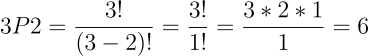
• נראה שיש 6 דרכים שונות לסדר מילים בנות 2 אותיות מ-3 אותיות אפשריות.

נוודא את התוצאה:

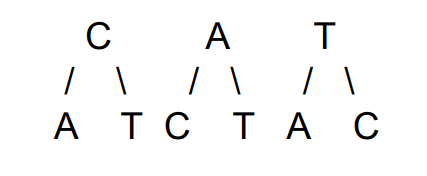
CA
CT
AC
AT
TA
TC

• בסה"כ 6 ענפים המהווים 6 תמורות שונות לסידור מילים בנות 2 אותיות מ-3 אותיות אפשריות.

אמרנו שהסדר חשוב במקרה של תמורות (פרמוטציות) אפשר לראות את זה בדוגמה של מספר האופנים לסידור A ו-B:

A B
B A

• לשתי המילים AB ו-BA אותו הרכב אבל בגלל שהסדר חשוב הם נחשבות לתמורות (פרמוציות) שונות של אותם 2 אותיות.

אפשר להשתמש בנוסחה לחישוב התמורה כשרוצים לחשב את מספר האפשרויות לסידור n פריטים מתוך אותו מספר n של פריטים. לדוגמה: כמה תמורות ישנם לסידור 3 פריטים?

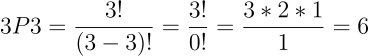
• שימו לב! אפס עצרת !0 שווה ל-1

חידות מילים ואותיות

כמה אפשרויות שונות קיימות לסידור האותיות במילה "שמש"?

1. בגלל שיש 3 אותיות : !3
2. בגלל שהאות "ש" חוזרת פעמיים נצמצם את מספר האפשרויות ב-!2

נחשב:

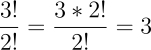
• למה לצמצם ב-!2? כי זה לא משנה באיזה "ש" משתמשים ראשונה או שנייה שתיהם מביאות לאותה תוצאה.

נראה בעיה נוספת.

כמה תמורות יש לסידור האותיות במילה "אספסופ"?

1. בגלל שיש 6 אותיות: !6
2. בגלל שהאות "ס" חוזרת פעמיים נצמצם ב-!2.
3. בגלל שהאות "פ" חוזרת פעמיים נצמצם ב-!2.

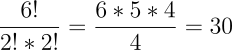
שילובים (קומבינציות)

שילוב (קומבינציה) הוא מספר הדרכים לסידור פריטים כשהסדר לא חשוב.

לדוגמה, אם עומדות לרשותנו האותיות A ו-B בלבד ניתן לשלב אותם באופן 1 בלבד כאשר הסדר לא חשוב. התוצאה תהיה השילוב (קומבינציה):

A B

• מדוע? בגלל ש-AB ו-BA הם אותו שילוב.

את אותו דבר אפשר לראות במקרה של 3 פריטים:

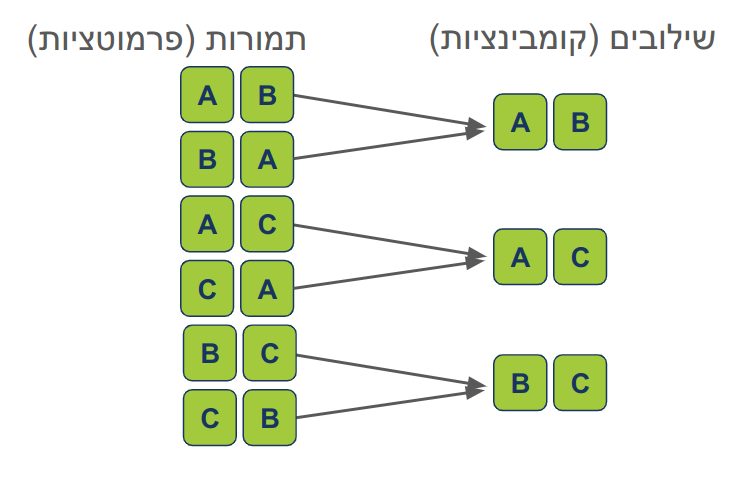
• אחרי צמצום הכפילויות נשארנו עם 3 קומבינציות במקום 6 פרמוטציות.

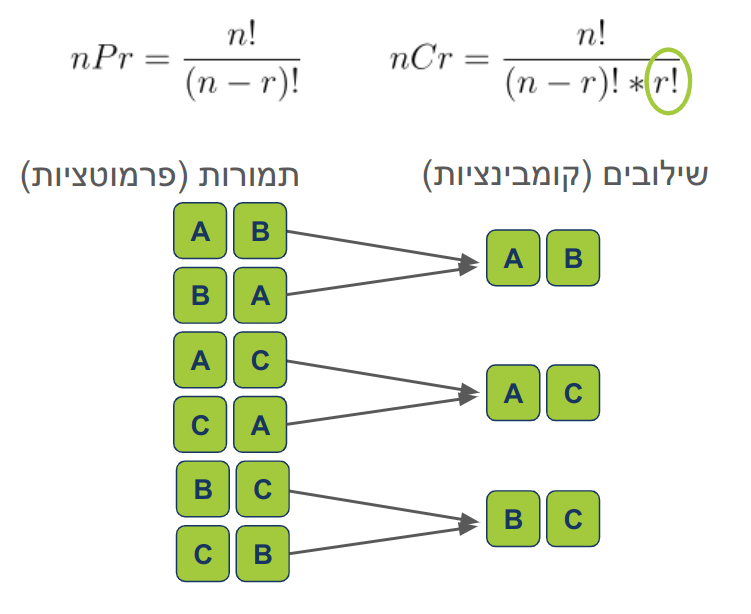
בגלל שאנחנו רוצים להסיר את הכפילויות הנוסחה לחישוב שילובים תהיה:

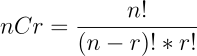
• הנוסחה מאוד דומה לחישוב תמורה מלבד החלוקה ב-!r כדי לצמצם את האפשרויות.

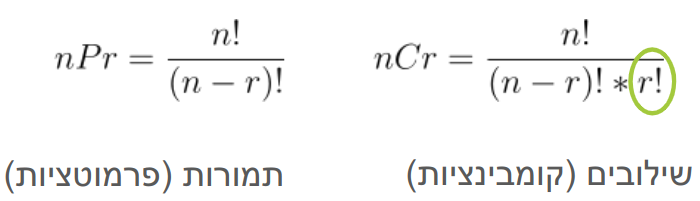
לדוגמה, נחשב את מספר השילובים (קומבינציות) לבחירת 2 פריטים מתוך 3:

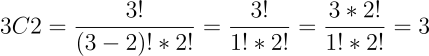
• !1 זה 1
• את !3 אפשר לכתוב כ-3*2!
• את !2 מבטלים כי הם נמצאים במונה ובמכנה

נסכם

במקרה של תמורות (פרמוטציות) הסדר משנה אולם במקרה של שילובים (קומבינציות) הסדר אינו משנה. זה חשוב כדי שנדע באיזה צורת חישוב להשתמש עבור המקרים השונים.

הנוסחה לחישוב מספר התמורות (פרמוטציות):

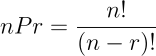
הנוסחה לחישוב מספר השילובים (קומבינציות):

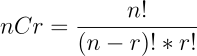
חידות

מתוך 10 שכנים אנחנו רוצים לבחור 3 שחקנים לנבחרת הקט-רגל של הבניין. כמה אפשרויות בחירה יש לנו?

השאלה הראשונה שאנחנו צריכים לשאול היא האם הסדר משנה. במקרה זה, הסדר אינו משנה. כי השחקנים שווים אחד לשני. זה לא משנה אם בחרנו את אותו שחקן ראשון, שני או שלישי כל עוד הוא נכנס לנבחרת. מכאן שהסדר לא משנה. וכשהסדר אינו משנה נחשב את מספר השילובים באמצעות הנוסחה לחישוב קומבינציות:

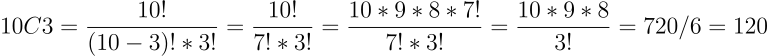
מתוך 10 אנשים אנחנו רוצים לבחור: מנהל, סגן ראשון וסגן שני. כמה אפשרויות בחירה יש לנו?

השאלה הראשונה שאנחנו צריכים לשאול היא האם הסדר משנה. וכן הסדר משנה כיוון שאם בחרנו נשיא אנחנו לא יכולים לבחור נשיא נוסף. ומכיוון שהסדר משנה נשתמש בנוסחה לחישוב תמורות פרמוטציות:

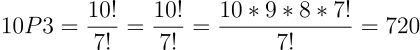
חישוב הסיכוי לזכייה בלוטו

אחרי שהבנו מה זה קומבינציות ואיך ניתן לחשב אותם אנחנו יכולים להשתמש בידע כדי לחשב את סיכויי הזכייה בלוטו.

אם יש 37 מספרים מתוכם צריך לבחור 6 כשהסדר לא חשוב הסיכוי לבחור נכונה על פי הנוסחה לחישוב שילובים (קומבינציות) הוא :

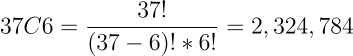
בנוסף, צריך לבחור מספר חזק 1 מתוך 7 אז נכפיל את התוצאה פי 7:

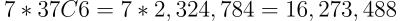
• המסקנה היא שהסיכוי לזכייה בלוטו בהנחה שצריך לבחור 6 מספרים מתוך 37, ובנוסף צריך לבחור 1 מתוך 7 מספרים הוא 1 ל- 16,273,488

במקום סיכום

שתי השאלות הבאות יעשו סדר בראש.

עליך לבחור את 3 השירים האהובים עליך ביותר לפי סדר מהאהוב ביותר ומטה מתוך רשימה של 10 שירים.

האם הסדר משנה? ודאי! אם כך נשתמש בנוסחת הפרמוטציה:

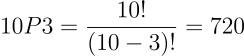
כמה אפשרויות יש לבחירת 3 שירים מרשימה של 10 שירים?

האם הסדר משנה? לא! אם כך נשתמש בנוסחת הקומבינציה:

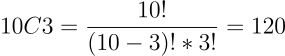
אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים