מה זה Gradient Descent ומה עושה אותו כל כך חשוב בלמידת מכונה?

Gradient Descent (GD) הוא אלגוריתם אופטימיזציה המשמש למציאת המינימום/מקסימום המקומי של פונקציה מתמטית. בלמידת מכונה, הוא משמש כדי למזער את פונקציית העלות cost function (למשל, ברגרסיה ליניארית).

למרות שקיימים מספר אלגוריתמי אופטימיזציה, הנפוץ שבהם, בכל הנוגע ללמידת מכונה, הוא Gradient Descent.

במדריך זה לא רק נסביר אודות Gradient Descent (GD) אלא בעיקר נכתוב קוד פייתון משלנו לביצוע האלגוריתם. את תוצאת הרצת הקוד תוכל לראות בסרטון:

כדי להבין אופטימיזציה, ראשית עלינו לענות על השאלה "מה לומד המחשב בתהליך למידת המכונה?" התשובה היא שהמחשב מפתח מודל ליצור תחזיות על סמך נתוני הקלט שהוא מקבל. במונחים מתמטיים, הפונקציה Y=F(X) מקבלת פרמטרים בתור קלט, X, ופולטת תחזית, Y.

לדוגמה, בהינתן שנות השכלה וגיל, המודל מנפק תחזית שכר. במסגרת תהליך הלמידה, הפרמטרים של הפונקציה נעשים מותאמים יותר ויותר לפתרון הבעיה. לדוגמה, אם המטרה של מודל ליניארי היא לתאר את הקשר בין גיל וציפיות שכר, המודל לומד את השיפוע והחיתוך עם ציר ה-Y אשר מתארים בצורה הטובה ביותר את השכר במציאות.

ככל שהתחזית קרובה יותר למציאות, כך המודל טוב יותר. בתהליך הלמידה, פונקציית העלות cost function מחשבת את השגיאה, שהיא המרחק בין חיזויי המודל לערכים בפועל. ככל שהשגיאה נמוכה יותר, כך המודל נחשב טוב יותר.

תהליך הלמידה ממזער את העלות למינימום בתהליך הנקרא gradient descent. התהליך הינו איטרטיבי משמע חוזר על עצמו מספר פעמים (epochs) עד שהמודל מגיע לנקודה שבה הוא מתכנס converge מפני שהוא לא יכול להשתפר יותר.

בפונקציה פשוטה כעין זו המתוארת בתרשים קל לראות היכן נמצאת נקודת המינימום:

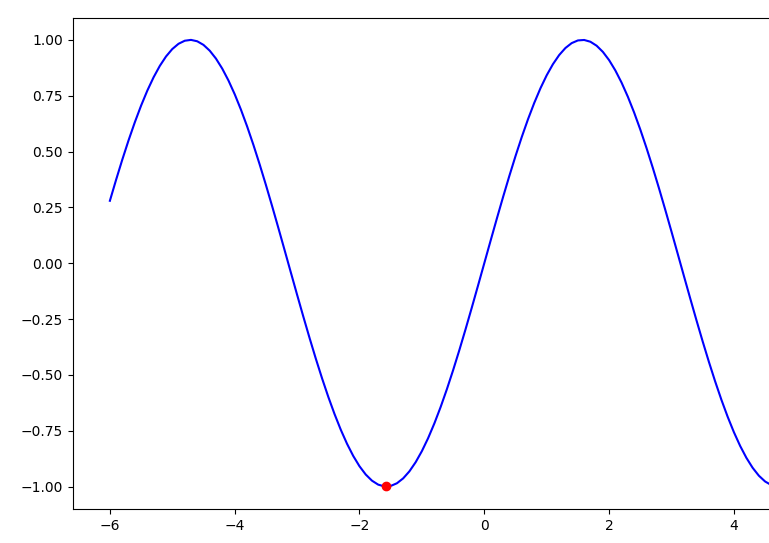
אך בעבודה על נתוני אמת ישנם משתנים (פיצ'רים) רבים וצורת הפונקציה עשויה להכיל כמה נקודות מינימום, חלקן מקומיות, מה שמקשה על איתור נקודת המינימום הגלובלית אותה התהליך שואף למצוא.

אנחנו לא יכולים לראות על כל נוף הפונקציה בגלל שנוף זה מורכב ומכיל משתנים רבים, אבל אנחנו יכולים לחשב את פונקציית העלות בנקודה אקראית ספציפית. ואז באמצעות back propagation, אנו יכולים להעריך את השיפוע השלילי של פונקציית העלות ולעשות צעד קטן בכיוון זה.

תהליך ה-Gradient Descent דומה לאדם שמנסה לרדת במדרון מהר כאשר מטרתו להגיע לתחתית ההר אך ערפל כבד מקשה עליו לראות היכן נמצאת התחתית. לכן, כדי להגיע לתחתית, הוא מתקדם קצת במדרון התלול ביותר שהוא מוצא. בכל פעם שהוא יורד קצת, הוא עושה הערכה מחודשת, וכך בסדרה של צעדים עוקבים, עד שהוא מגיע לתחתית.

Gradient descent הינו תהליך איטרטיבי. בכל צעד הוא מחשב את הנגזרת השלילית בנקודה, ואז מתקדם מעט בכיוון, וחוזר חלילה בסדרה של צעדים עוקבים כאשר ניתן לתאר את שלוש הצעדים הראשונים בתהליך באופן הבא:

• θ - הינו הפרמטר שפונקציית העלות עושה לו אופטימיזציה. לדוגמה, ברגרסיה לינארית θ יכול להיות שיפוע הפונקציה או נקודת החיתוך עם הצירים. בתיאור המתמטי לעיל θ היא הפרמטר בצעד: θ0 הינו הפרמטר בצעד הראשון, θ1 בצעד השני, וכיו"ב
• f(θ) - פונקציית העלות מחשבת את השגיאה בין הערכים שהמודל חוזה והערכים בפועל בהתבסס על ערכי הפרמטר הנוכחיים.
• gradient - מחשב את הגרדיאנט (הנגזרת) בנקודה, ולפיכך, gradient(f(θ)) מחשב את הנגזרת של פונקצית העלות ביחס לפרמטר θ. הנגזרת נותנת את השיפוע הגדול ביותר בנקודה. כדי לקבל את ההפחתה הגדולה ביותר בכל צעד כופלים במינוס.
• γ - הוא קצב הלמידה. מכפילים את הגרדיאנט בפרמטר γ כדי לאפשר לתהליך ה-Gradient descent להתקדם בצעדים קטנים כדי שלא יפספס את הנקודה.

הרעיון הוא שהנגזרת בנקודה נותנת את כיוון השיפוע התלול ביותר, ולכן אם לוקחים צעד בכיוון הנגדי ההפחתה היא בשאיפה הגדולה ביותר. חוזרים על צעד זה כמה פעמים שצריך עד שמגיעים למינימום או עד למספר מוגדר מראש של חזרות.

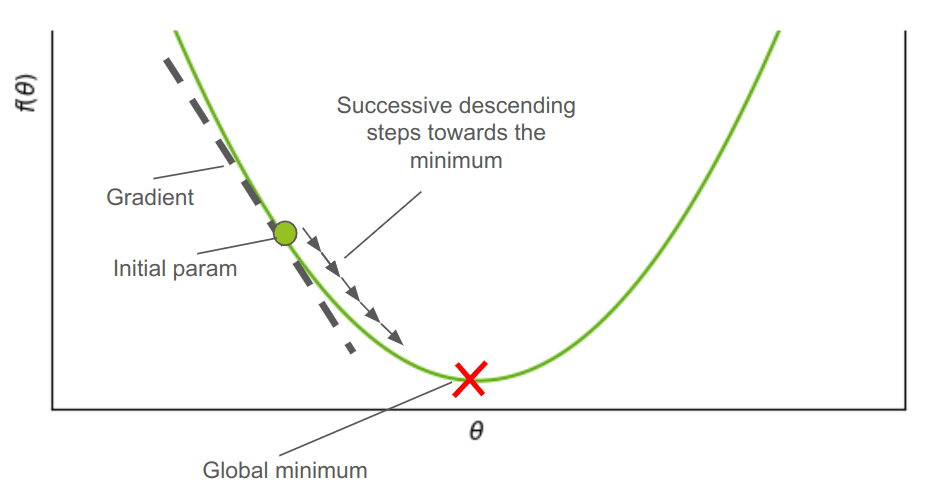
הסבר האיור במילים: Gradient Descent נעשה בסדרה של צעדים עוקבים שכל אחד מהם נעשה בכיוון השיפוע השלילי החד ביותר בכל נקודה כאשר המטרה היא למצוא את המינימום הגלובלי של הפונקציה.

קוד gradient descent משלנו באמצעות פייתון

לרוב, עובדים עם Gradient Descent של ספרייה, דוגמת TensorFlow, אבל זה מעניין לנסות לכתוב את הקוד בעצמנו כדי ללמוד. את הקוד נכתוב בפייתון.

נייבא את הספריות:

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

• ספריית numpy משמשת לעבודה עם מערכים ולביצוע חישובים, matplotlib בשביל סרטוט הגרפים והאנימציות.

נגדיר את הפרמטר γ, קצב הלמידה:

# The update rate should be small in each step to prevent underfitting
learning_rate = 0.01

במידה ושיעור ההתקדמות בין צעדים עוקבים בתהליך ה-gradient descent הוא קטן מדי יש להפסיקו. נגדיר פרמטר early_stopping שאם התהליך מתקדם בשיעור קטן ממנו יש לעצור את התהליך:

# Stop if the GD process causes update which is less than the specified value
early_stopping = 1e-4

נגדיר פונקציה שבה התהליך יצטרך למצוא את המינימום. פה בחרתי בפונקצית סינוס שיש לה נקודות מינימום סדירות ושוות ופרמטר יחיד המגדיר אותה:

# The function
def f(x):
   return np.sin(x)

• הפונקציות של למידת מכונה הם מסובכות בהרבה וכוללות פיצ'רים רבים. אז כמו שיש לנו x בפונקצית הסינוס הפשוטה שלנו, במציאות יתכנו פרמטרים רבים, כמספר הפיצ'רים אותם נוכל לבטא באמצעות x,y, z וכיו"ב

בשביל לחשב את הנגזרת בנקודה נשתמש בחוקי החדו"א כאשר נגזרת של סינוס היא קוסינוס:

# Here I derive manually
def derive(x):  
   return np.cos(x)

פונקצית הסינוס יכולה להשתרע עד אינסוף על ציר ה-x. בשביל הצרכים הצנועים שלנו נגדיר אותה בין הנקודות 6 למינוס 6:

# Define the range of x values
xs = np.arange(-6, 6, 0.1)

נאתחל את הפונקציה כדי שיהיה לתהליך ה-gradient descent מהיכן להתחיל לרוץ:

# Initialize the point that tracks the direction of the negative gradient at the point
# Using a list to allow updating its value
current_pos = [-4.6, f(-4.6)] 

• בלמידת מכונה בעולם האמיתי, מאוד קשה לדעת מהיכן להתחיל, אז מאתחלים את הפונקציה באקראי. פה בחרתי נקודה סמוכה למקסימום בשביל שיהיה מעניין.

נשרטט את הפונקציה בתוך הטווח, ועליה נקודה אדומה שתעקוב אחר התקדמות התהליך:

# Create a figure and axis
fig, ax = plt.subplots()

# Plot the function
ax.plot(xs, f(xs), color='blue')

# The initial point position
point, = ax.plot(current_pos[0], current_pos[1], 'ro')

בתוך הפונקציה update מתרחש תהליך ה-gradient descent במסגרתו הפונקציה עושה צעדים חוזרים ונשנים בכיוון ההפוך לנגזרת (גרדיאנט) בנקודה כיוון שזה הכיוון של הירידה החדה ביותר:

# Take repeated steps in the opposite direction of the gradient (or approximate gradient)
# of the function at the current point, because this is the direction of steepest descent.
def update(frame):
   # Declare current_pos as global to update its value
   global current_pos 
   
   # To update the point, derive at the point and go in the opposite direction
   # but do so in small steps controlled by multiplying with the learning rate
   new_x = current_pos[0] - learning_rate * derive(current_pos[0])
   new_y = f(new_x)
  
   current_pos = [new_x, new_y]
  
   # Update the position of the point
   point.set_data(current_pos[0], current_pos[1])
  
   print("Iteration number:", frame)

   return point,

נוסיף לתוך הפונקציה update תנאי לבדיקה האם ההתקדמות בין צעדים עוקבים הינה קטנה יותר מהפרמטר early_stopping ואם זה המצב אז נעצור את התהליך:

# Take repeated steps in the opposite direction of the gradient (or approximate gradient)
# of the function at the current point, because this is the direction of steepest descent.
def update(frame):
   # Declare current_pos as global to update its value
   global current_pos 
  
   # To update the point, derive at the point and go in the opposite direction
   # but do so in small steps controlled by multiplying with the learning rate
   new_x = current_pos[0] - learning_rate * derive(current_pos[0])
   new_y = f(new_x)
  
   # Check for early stopping
   if abs(new_x - current_pos[0]) < early_stopping:
       print("=== Early stopping ===")
       ani.event_source.stop()
  
   current_pos = [new_x, new_y]
  
   # Update the position of the point
   point.set_data(current_pos[0], current_pos[1])
  
   print("Iteration number:", frame)

   return point,

נריץ את האנימציה באמצעותה נעקוב אחר תהליך ה-gradient descent:

# Run the gradient descent process and plot the animation
ani = animation.FuncAnimation(fig=fig, func=update, frames=1000, interval=30)

plt.show()

וריאציות עיקריות של gradient descent

ישנן מספר וריאציות של Gradient Descent (GD) המשמשות למידת מכונה, לכל אחת יתרונות ומקרי שימוש אופייניים. להלן 3 וריאציות עיקריות:

• Batch Gradient Descent (BGD): זהו האלגוריתם הסטנדרטי של Gradient Descent. הוא מחשב את השיפוע של פונקציית העלות ביחס לפרמטרים של מערך האימון training set כולו. הבעיה עם BGD היא היותו איטי עבור מערכי נתונים גדולים מכיוון שהוא מחשב את השיפוע באמצעות כל דוגמאות האימון.

• (Stochastic Gradient Descent (SGD: מעדכן את הפרמטרים תוך שימוש בשיפוע של פונקציית העלות ביחס לדוגמת אימון בודדת בכל איטרציה. הוא מהיר יותר מ-BGD מכיוון שהוא מעבד רק דוגמה אחת של סט האימון בכל פעם. ל-SGD יש עדכונים "רועשים" יותר והוא עשוי לנוע סביב המינימום בלי למצוא אותו ועדיין הוא גם יכול לחמוק ממינימום מקומי.

• Mini-batch Gradient Descent: מיני-אצווה GD עושה פשרה בין BGD ל-SGD. הוא מעדכן את הפרמטרים באמצעות שיפוע המחושב על תת-קבוצה אקראית קטנה של מערך האימון (מיני-אצווה mini-batch). גישה זו משלבת את היתרונות של יציבות ההתכנסות של BGD ויעילות SGD.

פיתוחים נוספים של gradient descent משתמשים במומנטום ובקצב למידה אדפטיבי - גדול יותר כשרחוקים מהמינימום וקטן יותר כשמתקרבים. על השוואה בין השיטות השונות וכיצד להשתמש בהם בספרייה ללמידת מכונה תוכלו לקרוא במדריך פונקציות אופטימיזציה וכיצד לבחור את הפונקציה המתאימה ביותר למודל למידת המכונה.

אולי גם זה יעניין אותך?

רגרסיה קווית באמצעות TensorFlow 2

פונקציות אופטימיזציה וכיצד לבחור את הפונקציה המתאימה ביותר למודל למידת המכונה

Keras Tuner - לבחירת ההיפר-פרמטרים למודל למידת מכונה

לכל המדריכים בסדרה על למידת מכונה

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים