איך לכפול מספרים בינאריים?

מחבר:

בתאריך: 17.01.2024

כפל מספרים בינאריים הוא פשוט מכיוון שהוא מבוסס על אותם עקרונות כמו הכפל העשרוני - רק עם פחות ספרות. בוא נראה איך זה עובד.

חוקי הכפל הבינארי הם פשוטים מאוד, הרי הם לפניכם:

0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1

איך לכפול מספרים בינאריים?

כפל מספרים כרוך בהסטה וחיבור.

כופלים כל ביט (סיבית) של המספר השני (הכופל) במספר הראשון (הנכפל).

מסיטים את התוצאה מקום אחד לשמאל עבור כל ביט בכופל.

לבסוף, מחברים את התוצאות.

דוגמה 1:
101×11=?

דבר ראשון, ניישר את המספרים כך שכל ספרה מיושרת בטור הנכון:

 
1 0 1
× 1 1
-----
? ? ?

עובדים מימין לשמאל. תוך שכופלים כל ביט של הכופל בנכפל:

נתחיל מלכפול את הביט הימני ביותר של הכופל בנכפל: 1×101=101.
את התוצאה נכתוב בשורה הראשונה מתחת לקו:
```
 
  1 0 1
×   1 1
--------
  1 0 1
```
נעבור לביט השני מימין של הכופל ונכפול גם אותו בנכפל: 1×101=101.
את התוצאה נכתוב בשורת התוצאה השנייה תוך הסטה מקום אחד לשמאל:
```
 
  1 0 1
×   1 1
--------
  1 0 1
1 0 1
```
נחבר את תוצאות ההכפלה כמוסבר במדריך איך לחבר מספרים בינאריים?
```
 
    1 0 1
+ 1 0 1
  -------
  ? ? ? ?
```
נחבר את הטורים מימין לשמאל.

בטור הימני ביותר:
1+0=1
נרשום את התוצאה:
```
 
    1 0 1
+ 1 0 1
  -------
  ? ? ? 1
```
בטור השני מימין:
0+1=1
נרשום את התוצאה:
```
 
    1 0 1
+ 1 0 1
  -------
  ? ? 1 1
```
בטור השלישי מימין:
1+0=1
נרשום את התוצאה:
```
 
    1 0 1
+ 1 0 1
  -------
  ? 1 1 1
```
בטור הרביעי והאחרון:
0+1=1
נרשום את התוצאה:
```
 
    1 0 1
+ 1 0 1
  -------
  1 1 1 1
```

נאמת את התוצאה:

101 (בינארי) = 5 (עשרוני)
11 (בינארי) = 3 (עשרוני)
5×3=15
כל הכבוד!! החישוב שלנו נכון ✅

אם אתה רוצה להיזכר איך להמיר מספרים בינאריים לעשרוניים והפוך אתה מוזמן לקרוא את המדריך מהם מספרים בינאריים וכיצד להמיר מספרים מייצוג עשרוני לבינארי והפוך.

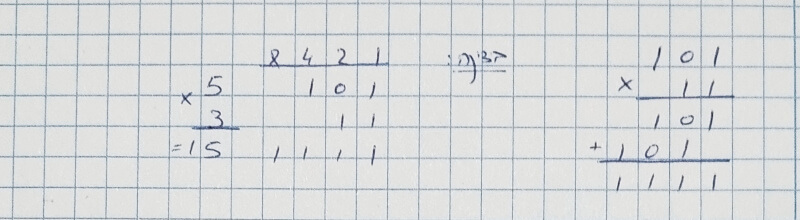
101x11=1111

דוגמה 2:
110×101=?

דבר ראשון, ניישר את המספרים כך שכל ספרה מיושרת בטור הנכון:

 
  1 1 0
× 1 0 1
--------
  ? ? ?

עובדים מימין לשמאל. תוך שכופלים כל ביט של הכופל בנכפל:

נתחיל מלכפול את הביט הימני ביותר של הכופל בנכפל: 1×110=110.
את התוצאה נכתוב בשורה הראשונה מתחת לקו:
```
 
  1 1 0
× 1 0 1
--------
  1 1 0
```
נעבור לביט השני מימין של הכופל ונכפול גם אותו בנכפל: 0×110=000.
את התוצאה נכתוב בשורת התוצאה השנייה תוך הסטה מקום אחד לשמאל:
```
 
  1 1 0
× 1 0 1
--------
  1 0 1
0 0 0
```
נעבור לביט השלישי מימין של הכופל ונכפול גם אותו: 1×110=110.
את התוצאה נכתוב בשורת התוצאה השלישית תוך הסטה של 2 מקומות לשמאל:
```
 
    1 1 0
  × 1 0 1
  --------
    1 1 0
  0 0 0
1 1 0
```
נחבר את תוצאות ההכפלה כמוסבר במדריך איך לחבר מספרים בינאריים?
```
 
      1 1 0
  + 0 0 0
+ 1 1 0
  ---------
  ? ? ? ? ?
```
נבחר את הטורים מימין לשמאל.
- כל מה שיש לנו בטר הימני ביותר הוא 0
  אז זה מה שנרשום בתור תוצאת הטור:
```
 
      1 1 0
  + 0 0 0
+ 1 1 0
  ---------
  ? ? ? ? 0
```
- בטור השני מימין:
  1+0=1
  נרשום את התוצאה:
```
 
      1 1 0
  + 0 0 0
+ 1 1 0
  ---------
  ? ? ? 1 0
```
- בטור השלישי מימין:
  1+0+0=1
  אז נרשום:
```
 
      1 1 0
  + 0 0 0
+ 1 1 0
  ---------
  ? ? 1 1 0
```
- בטור הרביעי מימין:
  0+1=1
  1 נרשום בתוצאה:
```
 
      1 1 0
  + 0 0 0
+ 1 1 0
  ---------
  ? 1 1 1 0
```
- בטור האחרון יש רק 1 אז זה מה שנרשום בתוצאה:
```
 
      1 1 0
  + 0 0 0
+ 1 1 0
  ---------
  1 1 1 1 0
```

נאמת את התוצאה:

110 (בינארי) = 6 (עשרוני)
101 (בינארי) = 5 (עשרוני)
5×6=30
כל הכבוד!! החישוב שלנו נכון ✅

110x101=11110

דוגמה 3:
111×111=?

לפני שנפתור צריך להבין 🤯 איך לחבר יותר מ-2 ספרות:

אם רוצים לחבר 2 אחדות אז 1+1=10 כי 2 בבינארי זה 10
אם רוצים לחבר 3 אחדות אז 1+1+1=11 כי 3 בבינארי זה 11
אם רוצים לחבר 4 אחדות אז 1+1+1+1=100 כי 4 בבינארי זה 100 מה שמחייב להעביר 2 לטור משמאל
הרעיון הוא להעביר 1 לשמאל על כל זוג אחדות שמחברים:
- אם מחברים 2 אחדות מעבירים 1
- אם מחברים 4 אחדות מעבירים 2 אחדות
- אם מחברים 6 אחדות מעבירים 3 אחדות

דבר ראשון נעמד את הטורים:

 
  1 1 1
× 1 1 1
---------
  ?  ?

נעבוד מימין לשמאל. תוך שכופלים כל ביט של הכופל בנכפל:

נתחיל מלכפול את הביט הימני ביותר של הכופל בנכפל: 1×111=111.
את התוצאה נכתוב בשורה הראשונה מתחת לקו:
```
 
  1 1 1
× 1 1 1
  -----
  1 1 1 
```
נעבור לביט השני מימין של הכופל ונכפול גם אותו בנכפל: 1×111=111.
את התוצאה נכתוב בשורת התוצאה השנייה תוך הסטה מקום אחד לשמאל:
```
 
  1 1 1
× 1 1 1
  --------
  1 1 1
1 1 1
```
נעבור לביט השלישי מימין של הכופל ונכפול גם אותו בנכפל: 1×111=111.
את התוצאה נכתוב בשורת התוצאה השלישית תוך הסטה של שני מקומות לשמאל:
```
 
    1 1 1
  × 1 1 1
  --------
    1 1 1
  1 1 1
1 1 1
```
- נחבר את תוצאות ההכפלה מימין לשמאל.
```
 
      1 1 1
  + 1 1 1
+ 1 1 1
  ---------
  ? ? ? ? ?
```
  - סכום הטור הראשון מימין הוא בהכרח 1, אז זה מה שנרשום מתחת לקו:
```
 
      1 1 1
  + 1 1 1
+ 1 1 1
  ---------
  ? ? ? ? 1
```
  - סכום הטור השני מימין הוא:
    1+1=10
    בהתאם נרשום 0 בתוצאה ונעביר ① לעמודה שמשמאל:
```
 
      ①
      1 1 1
  + 1 1 1
+ 1 1 1
  ---------
  ? ? ? 0 1
```
  - בטור השלישי מימין יש קצת אתגר כי צריך לחבר 4 אחדות:
    1+1+1+①=?
    התוצאה היא 4 בעשרוני שזה 100 בבינארי.
    מה עושים עם זה?
    נרשום 0 מתחת לקו, ונעביר שתי אחדות לטור משמאל:
```
 
    ①①
    ①1 1 1
+   1 1 1
+ 1 1 1
  ---------
  ? ? 0 0 1
```
  - בטור שמשמאל שוב יש לנו 4 אחדות, אז נעשה אותו דבר נרשום 0 מתחת לקו, ונעביר שתי אחדות לעמודה שמשמאל:
```
 
  ①①①
  ①①1 1 1
+   1 1 1
+ 1 1 1
  ---------
  ? 0 0 0 1
```
  - עכשיו נשאר לנו בטור השמאלי ביותר לחבר 3 אחדות, שבבינארי זה 11
    בהתאם, נרשום 1 בטור התוצאה של הטור, ונעביר 1 לטור הבא משמאל:
```
 
  ①①①
①①①1 1 1
+   1 1 1
+ 1 1 1
-----------
  1 0 0 0 1
```
  - בתהליך התווסף לנו טור חדש משמאל אז נרשום את סכומו מתחת לקו:
```
 
  ①①①
①①①1 1 1
+   1 1 1
+ 1 1 1
-----------
1 1 0 0 0 1
```

קיבלנו תוצאה! האם היא נכונה? נבדוק.

111 בבינארי זה 7 בעשרוני
7×7=49 שזה 110001 בבינארי.
יופי! אנחנו צודקים!! 🎉

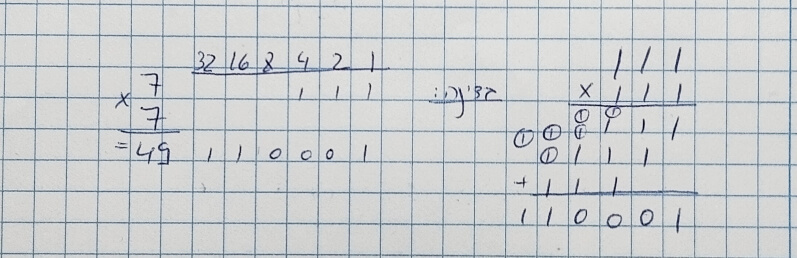
111x111=110001

דוגמה 4:
1101×1111=?

דבר ראשון נעמד את הטורים:

 
  1 1 0 1
× 1 1 1 1
  -------
    ? ? ?

נעבוד מימין לשמאל. תוך שכופלים כל ביט של הכופל בנכפל:

נתחיל מלכפול את הביט הימני ביותר של הכופל בנכפל: 1×1101=1101.
את התוצאה נכתוב בשורה הראשונה מתחת לקו:
```
 
  1 1 0 1
× 1 1 1 1
  -------
  1 1 0 1
```
נעבור לביט השני מימין של הכופל ונכפול גם אותו בנכפל: 1×1101=1101.
את התוצאה נכתוב בשורת התוצאה השנייה תוך הסטה מקום אחד לשמאל:
```
 
  1 1 0 1
× 1 1 1 1
  -------
  1 1 0 1
1 1 0 1
```
נעבור לביט השלישי מימין של הכופל ונכפול גם אותו בנכפל: 1×1101=1101.
את התוצאה נכתוב בשורת התוצאה השלישית תוך הסטה של שני מקומות לשמאל:
```
 
    1 1 0 1
  × 1 1 1 1
  ---------
    1 1 0 1
  1 1 0 1
1 1 0 1
```
נעבור לביט הרביעי מימין, ונכפול גם אותו בנכפל: 1×1101=1101.
את התוצאה נכתוב בשורת התוצאה הרביעית תוך הסטה של 3 מקומות לשמאל:
```
 
      1 1 0 1
    × 1 1 1 1
    ---------
      1 1 0 1
    1 1 0 1
  1 1 0 1
1 1 0 1
```
נחבר את תוצאות פעולת הכפל, כרגיל מימין לשמאל:
```
 
         1 1 0 1
    +  1 1 0 1
  +  1 1 0 1
+  1 1 0 1
  ------------
  ?  ?  ?  ?
```
- סכום הטור הראשון מימין הוא בהכרח 1, אז זה מה שנרשום מתחת לקו:
```
 
         1 1 0 1
    +  1 1 0 1
  +  1 1 0 1
+  1 1 0 1
  --------------
              1
```
- סכום הטור השני מימין הוא 0+1=1 אז נרשום זאת בשורת התוצאה:
```
 
         1 1 0 1
    +  1 1 0 1
  +  1 1 0 1
+  1 1 0 1
  --------------
            1 1
```
- סכום הטור השלישי מימין הוא:
  1+0+1=10
  בהתאם נרשום 0 בתוצאה ונעביר ① לעמודה שמשמאל:
```
 
       ①
       1 1 0 1
  +  1 1 0 1
+  1 1 0 1
+1 1 0 1
--------------
         0 1 1
```
- בטור הרביעי מימין יש קצת אתגר כי צריך לחבר 4 אחדות:
  1+1+1+①=?
  התוצאה היא 4 בעשרוני שזה 100 בבינארי.
  מה עושים עם זה?
  נרשום 0 מתחת לקו, ונעביר שתי אחדות לטור משמאל:
```
 
      ①①
      ①1 1 0 1
  +   1 1 0 1
+   1 1 0 1
+ 1 1 0 1
--------------
        0 0 1 1
```
- בטור החמישי מימין שוב צריך לחבר 4 אחדות:
  1+1+①+①=100
  אז נרשום 0 מתחת לקו, ונעביר שתי אחדות לטור משמאל:
```
 
      ①①
    ①①1 1 0 1
  + ①1 1 0 1
+   1 1 0 1
+ 1 1 0 1
--------------
      0 0 0 1 1
```
- בטור החמישי מימין שוב צריך לחבר 4 אחדות:
  1+1+①+①=100
  ולכן בנוהל נרשום 0 מתחת לקו, ונעביר שתי ① לטור משמאל:
```
 
      ①①
    ①①1 1 0 1
+① ①1 1 0 1
+① 1 1 0 1
+ 1 1 0 1
--------------
    0 0 0 1 1
```
- בטור השישי מימין צריך לחבר 3 אחדות:
  1+①+①=11
  בהתאם נרשום 1 מתחת לקו, ונעביר ① לטור חדש שנפתח משמאל:
```
 
       ①①
     ①①1 1 0 1
+①①①1 1 0 1
+  ①1 1 0 1
+  1 1 0 1
---------------
   1 0 0 0 1 1
```
- בטור האחרון כל מה שנשאר לנו לעשות הוא לכתוב 1 בתוצאה:
```
 
        ①①
      ①①1 1 0 1
+①①①1 1 0 1
+  ①1 1 0 1
+  1 1 0 1
---------------
  1 1 0 0 0 1 1
```

לא מסיימים עד שלא מוודאים!!

1101 בבינארי ≡ 13 עשרוני
1111 בבינארי ≡ 15 עשרוני
13×15=195 שזה בדיוק התוצאה שחישבנו: 1100011. 🚀!!

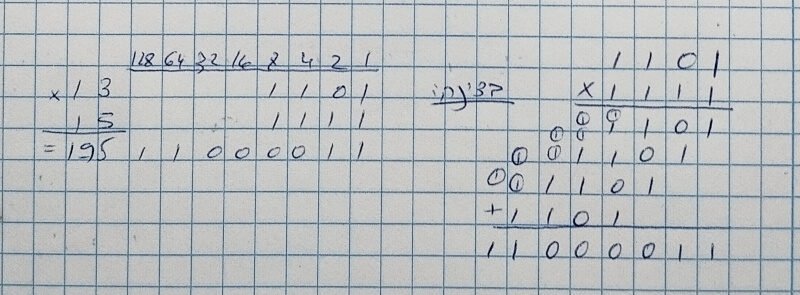
1101x1111=11000011

מדריכים נוספים שעשויים לעניין אותך

מהם מספרים בינאריים וכיצד להמיר מספרים מייצוג עשרוני לבינארי והפוך

איך לחבר מספרים בינאריים?

איך לחסר מספרים בינאריים?

איך לחלק מספרים בינאריים?

לכל המדריכים בסדרת כישורי מחשב באתר רשתטק

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים

המדריכים באתר עוסקים בנושאי תכנות ופיתוח אישי. הקוד שמוצג משמש להדגמה ולצרכי לימוד. התוכן והקוד המוצגים באתר נבדקו בקפידה ונמצאו תקינים. אבל ייתכן ששימוש במערכות שונות, דוגמת דפדפן או מערכת הפעלה שונה ולאור השינויים הטכנולוגיים התכופים בעולם שבו אנו חיים יגרום לתוצאות שונות מהמצופה. בכל מקרה, אין בעל האתר נושא באחריות לכל שיבוש או שימוש לא אחראי בתכנים הלימודיים באתר.

למרות האמור לעיל, ומתוך רצון טוב, אם נתקלת בקשיים ביישום הקוד באתר מפאת מה שנראה לך כשגיאה או כחוסר עקביות נא להשאיר תגובה עם פירוט הבעיה באזור התגובות בתחתית המדריכים. זה יכול לעזור למשתמשים אחרים שנתקלו באותה בעיה ואם אני רואה שהבעיה עקרונית אני עשוי לערוך התאמה במדריך או להסיר אותו כדי להימנע מהטעיית הציבור.

שימו לב! הסקריפטים במדריכים מיועדים למטרות לימוד בלבד. כשאתם עובדים על הפרויקטים שלכם אתם צריכים להשתמש בספריות וסביבות פיתוח מוכחות, מהירות ובטוחות.

המשתמש באתר צריך להיות מודע לכך שאם וכאשר הוא מפתח קוד בשביל פרויקט הוא חייב לשים לב ולהשתמש בסביבת הפיתוח המתאימה ביותר, הבטוחה ביותר, היעילה ביותר וכמובן שהוא צריך לבדוק את הקוד בהיבטים של יעילות ואבטחה. מי אמר שלהיות מפתח זו עבודה קלה ?

השימוש שלך באתר מהווה ראייה להסכמתך עם הכללים והתקנות שנוסחו בהסכם תנאי השימוש.

איך לכפול מספרים בינאריים?

איך לכפול מספרים בינאריים?

דוגמה 1:
101×11=?

דוגמה 2:
110×101=?

דוגמה 3:
111×111=?

דוגמה 4:
1101×1111=?

מדריכים נוספים שעשויים לעניין אותך

נכתב ע"י יוסי בן הרוש

הוסף תגובה חדשה

איך לכפול מספרים בינאריים?

דוגמה 1:101×11=?

דוגמה 2:110×101=?

דוגמה 3:111×111=?

דוגמה 4:1101×1111=?

מדריכים נוספים שעשויים לעניין אותך

נכתב ע"י יוסי בן הרוש

הוסף תגובה חדשה

דוגמה 1:
101×11=?

דוגמה 2:
110×101=?

דוגמה 3:
111×111=?

דוגמה 4:
1101×1111=?