סקריפט סימולציית מונטה קרלו להערכת השקעה

עוד יבואו ימים טובים.

שיטות מונטה קרלו Monte Carlo methods הם אלגוריתמים חישוביים המסתמכים על דגימה אקראית חוזרת כדי להשיג תוצאות מספריות. הרעיון הבסיסי הוא להשתמש באקראיות כדי לפתור בעיות קשות. הם משמשים לעתים קרובות בבעיות מתמטיות והם שימושיים ביותר כאשר קשה או בלתי אפשרי להגיע לפתרון אנליטי.

במקרה של השקעה בקרנות צמודות אינדקס, התשואה העתידית של הקרן תלויה במספר גורמים, כגון שיעור הריבית במשק, שער החליפין, והביצועים של המדד אליו קשורה הקרן. גורמים אלה אינם ידועים מראש, ולכן קשה לחשב את התשואה העתידית של הקרן באופן אנליטי.

שיטות מונטה קרלו יכולות לשמש כדי להעריך את התשואה העתידית של קרן צמודת אינדקס על ידי הרצת תרחישים שונים עבור גורמים אלו. לדוגמה, ניתן לדגום מתוך התפלגות סטטיסטית עבור שערי המניות בבורסה, ולחשב את התשואה העתידית של הקרן עבור כל תרחיש. לאחר מכן, ניתן להשתמש בנתונים אלו כדי לחשב את התשואה הצפויה של הקרן, כמו גם את הפיזור של התוצאות האפשריות.

שיטות מונטה קרלו יכולות להיות יעילות מאוד עבור הערכת תשואות של השקעות בבורסה. עם זאת, חשוב לזכור שהן מספקות הערכה בלבד, ולא ביטחון מוחלט לגבי התשואה העתידית של ההשקעה.

אני לא יועץ פיננסי, אלא מפתח מקצועי שנהנה לכתוב קוד ומתעניין מאוד בסטטיסטיקה. בין השאר, מעניין אותי הנושא של שימוש באלגוריתמים שאינם דטרמיניסטים לפתרון בעיות קשות, וכך הגעתי לרעיון לפתח סקריפט אשר מדמה התפתחות של השקעה צמודת קרן אינדקס לאורך שנים רבות באמצעות שיטות מונטה קרלו. על סמך מה שלמדתי פיתחתי את הסקריפט הבא שמקבל סכום התחלתי, שיעור השקעה חודשי, ומספר שנות השקעה ומנפק הערכה של תוצאות ההשקעה.

לדוגמה, אדם שמתחיל מהון התחלתי של 10,000, מפקיד לקרן מדי חודש 1,000 ומתמיד בכך במהלך 5 שנים.

התוצאה שקיבלתי שמסכמת 10,000 סימולציות מונטה קרלו היא:

• לכל היותר 170,00
• לכל הפחות 44,000
• ממוצע 86,000 עם סטיית תקן 85,000 (המגוון הוא רחב)
• חציון (שפחות מושפע מתוצאות קיצוניות ולכן נחשב אמין מהממוצע) : 84,000
• התוצאות ברבעון השלישי 75% והתחתון 25% אף הן מחושבות כדי להעריך את מידת הפיזור סביב החציון (IQR)

למה 10,000 סימולציות? כי חוק המספרים הגדולים מלמד שככל שנדגום יותר, כך ממוצע התוצאות שלנו ייטה להתכנס לתוצאה המיוחלת, והחיזוי יהיה מדויק יותר. זה נכון עבור שיטות מונטה קרלו, כמו גם עבור כל שיטת דגימה אקראית אחרת. במקרה של סימולציות פיננסיות, חשוב להריץ מספיק סימולציות כדי לקבל תוצאה אמינה. 10,000 סימולציות הוא מספר טוב להתחלה, אך ניתן להגדיל את מספר הסימולציות אם רוצים לקבל תוצאה מדויקת יותר. כמובן, ישנם גם שיקולים מעשיים שיש לקחת בחשבון בעת קביעת מספר הסימולציות. מספר הסימולציות משפיע על משך זמן הריצה של הסימולציה. אם אתה משתמש במחשב חזק, אתה יכול להריץ מספר גדול של סימולציות מבלי להאריך משמעותית את משך הריצה. עם זאת, אם אתה משתמש במחשב חלש יותר, ייתכן שיהיה עליך להסתפק במספר קטן יותר של סימולציות.

כך נראות התוצאות של 12 סימולציות מתוך 10,000 (כולל את התוצאות הגבוהות ביותר, הנמוכות ביותר וכמה אקראיות):

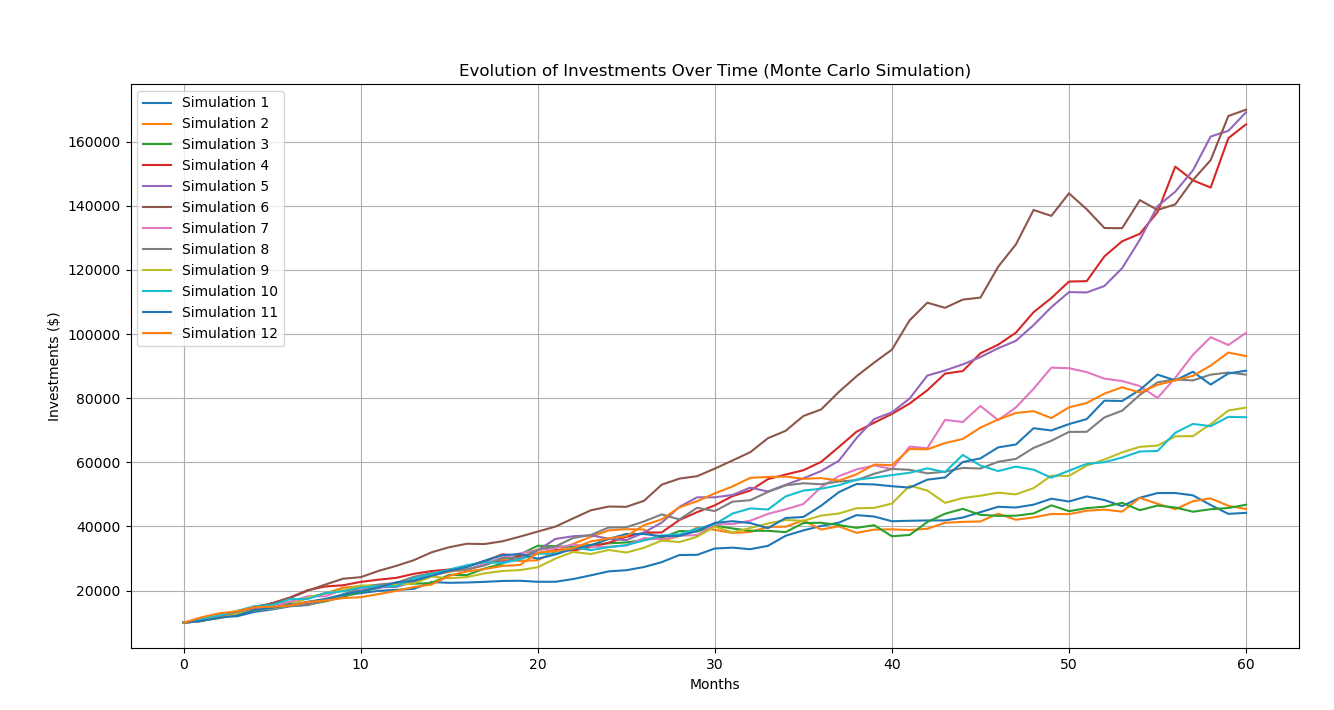
השתמשתי ב-numpy בשביל החישובים וב-matplotlib בשביל התרשימים.

אילו המשתנים הבסיסיים שהזנתי:

num_simulations = 10000
initial_balance = 10000
investment_years = 5
monthly_contribution = 1000
investment_returns_mean = 0.07
investment_returns_volatility = 0.12

• ההנחה שלי היתה ששיעור ההשתנות הממוצע של הבורסה הינו 7% עם שונות של 12%, וזה על פי מה שמצאתי על הבורסה האמריקאית (על תשאלו אותי איזה מהם). על פי הנתונים ההיסטוריים, שיעור ההשתנות הממוצע של הבורסה האמריקאית הוא כ-7%. שונות של 12% היא שונות גבוהה, אך היא סבירה בהתחשב בכך שהבורסה האמריקאית היא בורסת מניות, ושהתשואות של מניות יכולות להיות תנודתיות מאוד. כמובן, חשוב לזכור שהנתונים ההיסטוריים אינם ערובה לעתיד. השוק הפיננסי הוא מערכת דינמית, והתנהגותו יכולה להשתנות עם הזמן. לכן, חשוב להשתמש בהנחות בזהירות, ולהיות מוכן לכך שהתוצאות של הסימולציה שלך עשויות להיות שונות מהתוצאות האמיתיות.

הלב של הקוד הוא החלק שמבצע את סימולציות מונטה קרלו. הבחירה ברירת המחדל היא בשיטת מונטה קרלו אשר דוגמת מתוך התפלגות נורמלית באמצעות המתודה:

investment_returns_all = np.random.normal(
           loc=investment_returns_mean / 12,
           scale=investment_returns_volatility / np.sqrt(12),
           size=(num_simulations, investment_years * 12)
       )

בדקתי באינטרנט וראיתי שיש מי שמשתמש בהתפלגויות אחרות בשביל סימולציות המגלמות סיכון פיננסי, דוגמת התפלגות ע"ש Cauchy שדומה להתפלגות הנורמלית הודות לעקומת הפעמון עם רוב התוצאות במרכז, אבל הזנב הארוך הוא עבה יותר, בהתאמה עם הנטייה של השווקים לאירועי קיצון. כך נראית סימולציה שהרצתי עם התפלגות Cauchy:

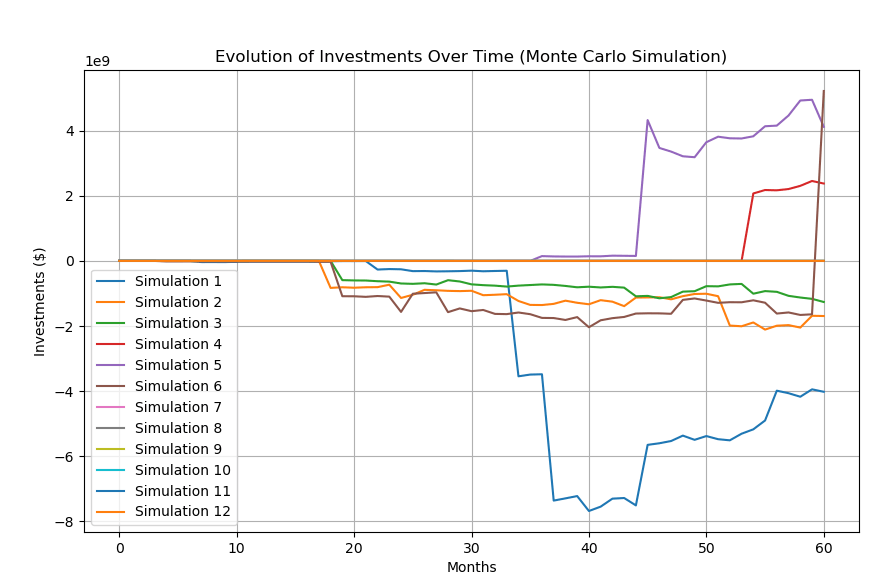
את התוצאה הזו קיבלתי אחרי שהשתמשתי במתודה הבאה:

location = investment_returns_mean / 12
       scale = investment_returns_volatility / np.sqrt(12)
      
       investment_returns_all = cauchy.rvs(loc=location, scale=scale, size=(num_simulations, investment_years * 12))

ניסיתי גם את ההתפלגויות, log-normal ו-Generalized Extreme Value שגם הם רציפות ומגלמות אירועי קיצון, אלא שהתוצאות שקיבלתי היו מדי קיצוניות. בכל זאת כללתי גם אותם כאפשרות בפונקציה שמייצרת את החיזויים, אולי יהיה מי שיפיק מהם תועלת.

זה הקוד המלא. תשחקו איתו באחריות:

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import cauchy
from scipy.stats import genextreme


np.random.seed(42)  # Set a seed for reproducibility


# Input parameters for the simulation
num_simulations = 10000
initial_balance = 10000
investment_years = 5
monthly_contribution = 1000
investment_returns_mean = 0.07
investment_returns_volatility = 0.12


# Simulate investments evolution over time
def monte_carlo_investments_simulation(num_simulations,
                                  initial_balance,
                                  investment_years,
                                  monthly_contribution,
                                  investment_returns_mean,
                                  investment_returns_volatility,
                                  distribution='normal'):


   # Generate random investment returns for all simulations and months at once
   # Pick one of these distributions which are suitable for risk assessment
   if distribution == 'cauchy':
       # Set parameters for Cauchy distribution
       location = investment_returns_mean / 12
       scale = investment_returns_volatility / np.sqrt(12)
      
       investment_returns_all = cauchy.rvs(loc=location, scale=scale, size=(num_simulations, investment_years * 12))
   elif distribution == 'lognormal':
       # Use log-normal distribution
       investment_returns_all = np.random.lognormal(
           mean=np.log(1 + investment_returns_mean / 12),
           sigma=investment_returns_volatility / np.sqrt(12),
           size=(num_simulations, investment_years * 12)
       )
   elif distribution == 'gev':
       # Set parameters for GEV (=Generalized Extreme Value) distribution
       c = 0.2  # Shape parameter (needs to be adjusted based on domain knowledge)
       location = investment_returns_mean / 12
       scale = investment_returns_volatility / np.sqrt(12)


       investment_returns_all = genextreme.rvs(c, loc=location, scale=scale, size=(num_simulations, investment_years * 12))
   else:
       # Use normal distribution by default
       investment_returns_all = np.random.normal(
           loc=investment_returns_mean / 12,
           scale=investment_returns_volatility / np.sqrt(12),
           size=(num_simulations, investment_years * 12)
       )
      
   # Initialize array to store balances for each simulation
   balances_all = np.zeros((num_simulations, investment_years * 12 + 1))
   balances_all[:, 0] = initial_balance


   # Calculate balances for all simulations
   for month in range(investment_years * 12):
       # Update balances for the month, considering the compounding effect
       balances_all[:, month + 1] = balances_all[:, month] * (1 + investment_returns_all[:, month]) + monthly_contribution


   return balances_all






# Run the Monte Carlo simulation
simulation_results = monte_carlo_investments_simulation(num_simulations,
                                                   initial_balance,
                                                   investment_years,
                                                   monthly_contribution,
                                                   investment_returns_mean,
                                                   investment_returns_volatility,
                                                   distribution='normal')


# Summarize the end results
last_values = simulation_results[:, -1]


# Calculate summary statistics
first_quartile = np.percentile(last_values, 25)
third_quartile = np.percentile(last_values, 75)
iqr = third_quartile - first_quartile


print("Max:", np.max(last_values))
print("Min:", np.min(last_values))
print("First Quartile:", first_quartile)
print("Third Quartile:", third_quartile)
print("Interquartile Range (IQR):", iqr)
print("Median:", np.median(last_values))
print("Mean:", np.mean(last_values))
print("Standard Deviation:", np.std(last_values))




# Get indices that would sort the last values in ascending order
sorted_indices = np.argsort(simulation_results[:, -1])


# Pick 3 from the lowest results
lowest_results_indices = sorted_indices[:3]
lowest_results = simulation_results[lowest_results_indices]


# Pick 3 from the top results
top_results_indices = sorted_indices[-3:]
top_results = simulation_results[top_results_indices]


# Pick 6 random results
random_indices = np.random.choice(simulation_results.shape[0], size=6, replace=False)
random_results = simulation_results[random_indices]


# Combine into a single array
combined_results = np.concatenate([lowest_results, top_results, random_results])


# Plot the results
months = np.arange(0, investment_years * 12 + 1)
plt.figure(figsize=(10, 6))


for i in range(combined_results.shape[0]):
   plt.plot(months, combined_results[i], label=f'Simulation {i + 1}')


plt.xlabel('Months')
plt.ylabel('Investments ($)')
plt.title('Evolution of Investments Over Time (Monte Carlo Simulation)')
plt.legend()
plt.grid(True)
plt.show()

מדריכים נוספים שעשויים לעניין אותך

מה זה A/B testing - בדיקת A/B?

איך להציג סדרות זמן של נתונים באמצעות matplotlib?

משפט הגבול המרכזי - תנאי ללמידת מכונה על נתונים לא נורמליים

לכל המדריכים בנושא של למידת מכונה

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים