big-O ביטוי ליעילות הקוד

אחד הנושאים החשובים ביותר שחייבים לעניין כל מתכנת הוא האם הקוד שלו יעיל. זה חשוב כי קוד לא יעיל מאט תהליכים ועלול לגרום לקריסה של המערכת או לנזק כספי משמעותי. ביטוי big-O מתאר את התארכות משך הזמן של ביצוע משימה ביחס לגידול כמות המידע בו מזינים את התהליך.

במדריך זה נציג כמה אופנים נפוצים לתיאור התארכות משך הזמן לביצוע הקוד ביחס לכמות המידע באמצעות ביטוי big-O notation.

זמן ריצה קבוע O(1)

קוד שמשך זמן הביצוע שלו קבוע ללא תלות בכמות המידע שמזינים לתוכו מתואר כ- O(1).

• ה-O ואחריו סוגריים עגולים הם מוסכמה כשרוצים לתאר אלגוריתם באמצעות big-O.
• 1 בתוך הסוגריים העגולים מתאר זמן ריצה קבוע.

לדוגמה, פונקציה אשר מקבלת רשימה כפרמטר ובוחנת האם הערך של הפריט הראשון ברשימה הוא 1:

def is_first_1(list):
    print(list[0] == 1)

נזין אותה בטווח של ערכים שמתחיל מ-0, ונבדוק האם הפריט הראשון ברשימה הוא 1:

numbers = range(3)
is_first_1(numbers)

התוצאה:

False

• זה לא משנה מה אורך הרשימה זמן הביצוע יהיה קבוע פחות או יותר כי משך הזמן שלוקח למחשב להציב ערך לפריט מסוים ברשימה לא משתנה לא משנה כמה ארוכה הרשימה.

קוד שמשך הזמן של הביצוע שלו נותר קבוע ללא תלות בכמות המידע שמזינים לתוכו מכונה O(1).

כשהרצתי את הקוד על מספר מערכים שאורכם נע בין 10 ל-10 מיליון קיבלתי תוצאה שהיא כמעט קו ישר אופקי:

• ציר ה-X הוא N - מספר הפריטים בקלט. ציר ה-Y הוא משך הריצה של הפונקציה בשניות.
• בסה"כ ההתנהגות היא כמצופה. את הקפיצה בהתחלה אפשר להסביר על ידי תהליכים אחרים שלא קשורים באלגוריתם עצמו שמכניסים רעש לתוצאות.

גידול קווי במשך זמן הריצה O(N)

קוד שמשך הריצה שלו מתארך באופן קווי (ליניארי) ככל שגדלה כמות המידע שמזינים לתוכו מכונה O(N).

• ה-O ואחריו סוגריים עגולים הם מוסכמה כשרוצים לתאר אלגוריתם בשיטת big-O.
• N הוא משתנה המתאר את מספר הפריטים שמקבלת פונקציה כקלט (input).

לדוגמה, פונקציה שבודקת האם מספר מסוים קיים בתוך רשימה של מספרים:

def has_number(numbers, number):
    for num in numbers:
        if num == numbers:
            return True
        
    return False

numbers = range(100)
has_number(numbers, 101)

התוצאה:

False

• בתוך הפונקציה יש לולאה אשר רצה עד שהיא מוצאת את המספר, ואם היא מוצאת היא מחזירה True.
• במידה והמספר לא קיים במערך, הלולאה מסיימת לרוץ על כל הפריטים ואחרי שהיא מסיימת היא מחזירה False.

במקרה הטוב הלולאה תרוץ פעם אחת, תמצא התאמה כבר בפריט הראשון ותחזיר True. במקרה הגרוע, הלולאה תרוץ על כל המערך ורק אז תחזיר False.

בשביל big-O מה שמעניין הוא בדרך כלל המקרה הגרוע ביותר.

במקרה שלנו, משך הריצה של הפונקציה מתארך באופן קווי ככל שהפונקציה מקבלת רשימה ארוכה יותר כי מה שמעניין אותנו הוא המקרה הגרוע ביותר, שבו הפונקציה רצה את כל הרשימה עד סופה.

כדי לבחון את התארכות משך הריצה של הפונקציה נעביר רשימות הולכות ומתארכות של אפסים (10 אפסים, 100, אלף וכיו"ב) ונבחן את התארכות משך הריצה.

נייבא את הספריות:

import time
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

נריץ את הפונקציה על רשימות של אפסים שאורכם נע בין 10 למיליון:

ranges = [10**e for e in range(1,7)]
deltas = []
for n in ranges:
    numbers = [0]*n
    start = time.process_time()
    has_number(numbers, -1)
    end = time.process_time()
    delta = end-start
    deltas.append(delta)

• הפונקציה בודקת אם המספר 1 קיים ברשימה המורכבת כולה מאפסים כי המקרה הגרוע ביותר הוא כאשר מספר לא קיים ברשימה, ומה שמעניין אותנו הוא המקרה הגרוע ביותר.
• אספנו את משך הזמן שהפונקציה רצה לרשימה deltas.

נציג בטבלה את משך הריצה כתלות ב-N:

df = pd.DataFrame(list(zip(ranges, deltas)), columns=['n', 'time'])
df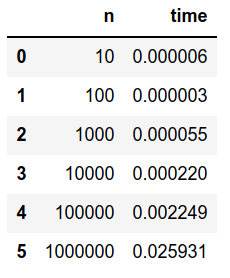

נציג את משך הריצה כתלות ב-N באמצעות תרשים שתייצר בשבילנו הפונקציה:

def plot_graph(df, title, ylim_to=0.1):
    plt.figure(figsize=(9, 6))
    plt.plot(df['n'], df['time'])
    plt.xlabel('N', fontsize=20)
    plt.ylabel('time(s)', fontsize=18)
    plt.ylim([0, ylim_to])
    plt.title(title, fontsize=24)

התוצאה:

plot_graph(df, "O(N)", 0.03)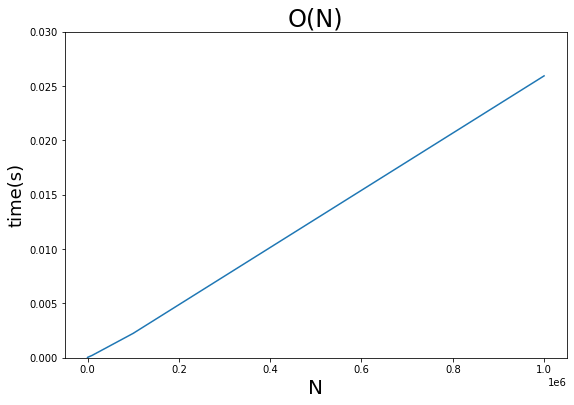

• רואים עלייה ליניארית בזמן הריצה של הפונקציה בהתאם להתארכות הרשימה.

אלגוריתם ליניארי אינו יעיל במיוחד כיוון שמשך הריצה שלו גדל בהתאם לכמות המידע שהוא מקבל.

קצב גידול לוגריתמי O(logN)

בחלק הקודם ראינו פונקציה שמחפשת מספר בתוך רשימה של מספרים. היא מתחילה מהפריט הראשון ברשימה ורצה כמה שצריך עד למציאת התאמה. מה שגורם לתלות ליניארית בין כמות הפריטים ומשך הריצה. הבעיה עם אלגוריתם ליניארי שהוא אינו יעיל במיוחד. הפתרון יכול להיות פונקציה לוגריתמית.

אלגוריתם חיפוש יעיל במיוחד משתמש בחיפוש בינארי binary search. הוא כולל את השלבים הבאים:

1. מקבל רשימה מסודרת. לדוגמה, מספרים מסודרים בסדר עולה.
2. חוצה את הרשימה לשניים ובודק האם הפריט באמצע הרשימה הוא המספר המבוקש.
3. אם הפריט האמצעי הוא גדול מהמספר שמחפשים עובר לחפש ברשימה השמאלית. אם קטן יותר, יחפש בימנית.
4. בשביל לחפש בתת-הרשימה הוא יחצה גם אותה לשניים, וחוזר חלילה עד למציאת הפריט המבוקש.

האלגוריתם binary search ממשיך לחצות את הרשימה לחצאים שאורכם הולך וקצר עד למציאת הערך המבוקש.

בכל פעם שאנחנו נתקלים באלגוריתם שמחלק רשימות לשניים אנחנו יכולים לחשוד שה big-O שלו הוא לוגריתמי.

נכתוב את קוד האלגוריתם binary search:

def binary_search(array, x):
    low = 0
    high = len(array) - 1
    
    while low <= high:
        # find the median
        mid = (high + low)//2
        
        # if the median is the value you
        # search for return true
        if array[mid] == x:
            return True
        
        # if the value is smaller than the median
        # search in the lower half of the list
        elif x < array[mid]:
            high = mid - 1
        # otherwise search in the upper half
        else:
            low = mid + 1

    return False

קוד שמחלק את הבעיה לחצי בכל פעם שמריצים אותו גורם לקשר לוגריתמי בין כמות המידע להתארכות משך זמן הריצה. כי הכפלת כמות המידע פי-2 גורמת להוספת סיבוב 1 לריצה. לדוגמה, בשביל רשימה באורך 2 פריטים הלולאה תרוץ לכל היותר פעמיים. עבור 4 פריטים - לכל היותר 3. עבור 8 פריטים לכל היותר 4. וכיו"ב. זה גידול לוגריתמי המתואר באמצעות ביטוי: O(log N).

זו תוצאה של ניסוי שמראה את התארכות משך זמן החיפוש של האלגוריתם ככל שגדל מספר הפריטים:

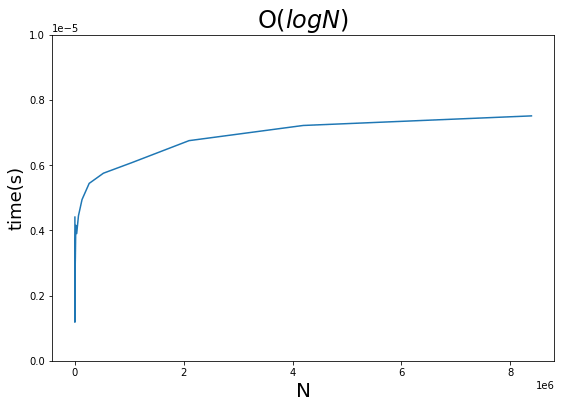
התהליך אשר חוצה את הרשימה בכל פעם לחצי גורם לקצב התארכות מהיר יותר של זמן הביצוע עבור רשימות קצרות אבל העקום מציג התמתנות בקצב הגידול ככל שמספר הפריטים גדל.

התרשים הבא משווה את ביצועי האלגוריתם הלוגריתמי מסוג O(log N) כנגד אלגוריתם בעל קצב גדילה ליניארי O(N):

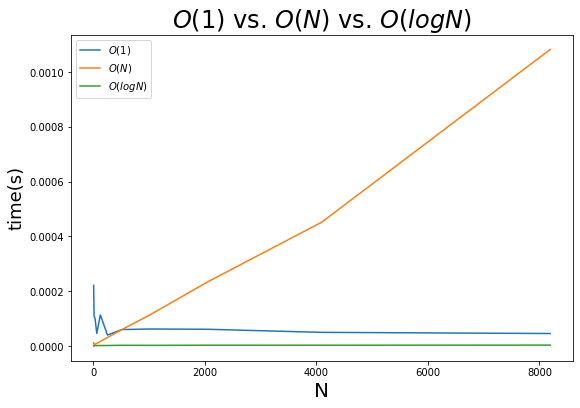
• אפילו במספרים נמוכים של כמה מאות ואלפים אפשר לראות את האלגוריתם הלוגריתמי מפגין ביצועים טובים בהרבה מאשר הליניארי.

אלגוריתמים לוגריתמיים המתוארים כ-O(log N) הם יעילים ביותר עבור כמות גדולה של נתונים. מוטב להשתמש בהם כמה שיותר.

גידול לינאריתמי במשך זמן הריצה O(N log N)

לא תמיד אפשר להשתמש באלגוריתם לוגריתמי. לדוגמה, כשרוצים לסדר רשימות לפי סדר מסויים מהגבוה לנמוך או הפוך אין בנמצא אלגוריתם לוגריתמי. זה מפני שסידור רשימות דורש מאיתנו להסתכל על כל פריט ברשימה לפחות פעם אחת. המשמעות היא שהכי טוב שאנחנו יכולים להשיג הוא O(N). האלגוריתמים הטובים ביותר בתחום מגיעים ל-O(N log N) מכונה linearithmic לינאריתמי. לדוגמה, quicksort.

אלגוריתם quicksort המקבל רשימת מספרים לא מסודרת:

1. בוחר פריט אקראי מתוך רשימת המספרים ומשתמש בו בתור ציר pivot.
2. מריץ לולאה על הרשימה ומשווה כל אחד מהמספרים ברשימה אל ה-pivot. התוצאה היא מיון של המספרים ל-3 רשימות: אחת שהיא גדולה מה-pivot, שנייה שווה ל-pivot, ושלישית גדולה יותר.
3. רשימות המספרים השונות מה-pivot מועברות כפרמטר לאלגוריתם כדי שיסדר גם אותם. התוצאה היא תהליך רקורסיבי באמצעותו מסודרות רשימות הולכות וקטנות מתוך הרשימה המקורית וממוזגות לרשימה מסודרת

הפונקציה הבאה מיישמת את האלגוריתם:

from random import choice

def quickSort(arr):
    # base case
    if len(arr) < 2:
        return arr
    
    # recursive case
    biggers = []
    smallers = []
    equals = []
        
    pivot = choice(arr)
    
    for num in arr:
        if num < pivot:
            smallers.append(num)
        elif num > pivot:
            biggers.append(num)
        else:
            equals.append(num)

    return quickSort(smallers) + equals + quickSort(biggers)

נפעיל את הפונקציה על רשימה קצרה של מספרים:

quickSort([128, 3, -1, 5, 2, 1, 4, 7, 3, 9, -1, 22])

התוצאה:

[-1, -1, 1, 2, 3, 3, 4, 5, 7, 9, 22, 128]

התרשים הבא משווה את ביצועי האלגוריתם הלינאריתמי quicksort עם אלגוריתם ליניארי ולוגריתמי binary search:

גידול פולינומי במשך זמן הריצה O(N^2)

קוד שמשך הריצה שלו מתארך בהתאם לריבוע כמות המידע שהוא מקבל מכונה O(N^2).

סיבה עיקרית לגידול פולינומי המתואר באמצעות O(N^2) הינו קוד אשר מריץ לולאה מקוננת. לולאה בתוך לולאה.

לדוגמה, פונקציה המקבלת רשימת מספרים, וכופלת כל מספר ברשימה בכל המספרים ברשימה, ולשם כך היא נעזרת בשתי לולאות מקוננות:

def multi_num(numbers):
    res = []
    for i in numbers:
        for j in numbers:
            res.append(i * j)
    return res

נריץ אותה על רשימה של מספרים בין 0 ל-9:

multi_num(range(10))

[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 0, 7, 14, 21, 28, 35, 42, 49, 56, 63, 0, 8, 16, 24, 32, 40, 48, 56, 64, 72, 0, 9, 18, 27, 36, 45, 54, 63, 72, 81]

כדי לבחון את התמשכות הריצה ככל שמזינים יותר נתונים הרצתי את הפונקציה על רשימות באורכים שונים:

ranges = [2**e for e in range(3,14)]
deltas = []
for r in ranges:
    numbers = [n for n in range(r)]
    start = time.process_time()
    multi_num(numbers)
    end = time.process_time()
    delta = end-start
    deltas.append(delta)

התוצאות מתוארות באמצעות הגרף הבא:

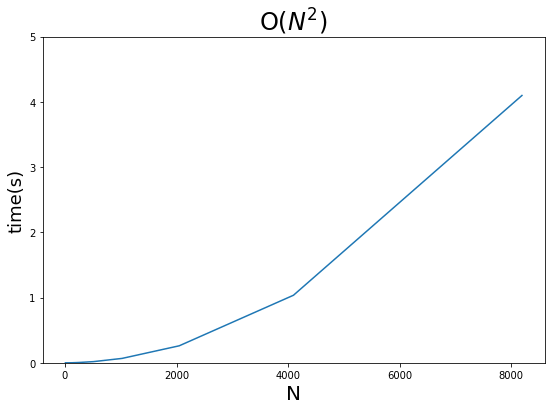
לא ניסיתי להריץ על רשימות ארוכות מ-8,192 פריטים בגלל שמשך הריצה קופץ מהר מאוד כשעובדים עם אלגוריתמים פולינומים מסוג O(N^2).

את התמשכות זמן הריצה של פונקציה מקוננת נתאר באמצעות O(N^2). באופן דומה, זמן ריצה של 3 לולאות מקוננות יתואר באמצעות big-O של O(N^3). של 4 לולאות באמצעות O(N^4). וכיו"ב. הקטסטרופה רק מעצימה ככל שמקננים יותר לולאות.

התרשים הבא משווה את ביצועי האלגוריתם הפולינומי מסוג O(N^2) כנגד אלגוריתם בעל קצב גדילה ליניארי O(N) ולוגריתמי O(logN):

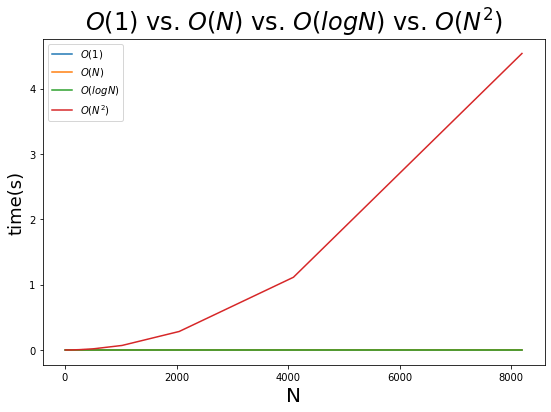
• אפילו במספרים נמוכים של כמה מאות ואלפים אפשר לראות את ההדרדרות ביכולת הביצוע של האלגוריתם הפולינומי O(N^2) שהוא הרבה יותר גרוע אפילו מאלגוריתם ליניארי O(N).

העובדה שפונקציות שכתובות בצורה לא נכונות יכולות לצאת משליטה הם סיבה שבגללה צריך להיות מודע ל-big-O. מה שראינו גם צריך ללמד אותנו שצריך להימנע מלולאות מקוננות (לולאה בתוך לולאה) כמה שאפשר בקוד שלנו.

העובדה שפונקציות שכתובות בצורה לא נכונות יכולות לצאת משליטה הם סיבה שבגללה צריך להיות מודע ל-big-O.

קצב גידול אקספוננציאלי הידוע בכינויו "תמצא אלגוריתם יעיל יותר"

אם משך הריצה של הקוד שלך גדל באופן אקספוננציאלי אז אתה בבעיה.

לדוגמה, הקוד הבא מוצא את סדרת פיבונאצ'י עבור המספרים שמעבירים אליו:

def fibonaci(number):
    if number <= 1:
        return number
    return fibonaci(number-1)+fibonaci(number-2)

כל מספר בסדרת פיבונאצ'י הוא הסכום של שני המספרים שקדמו לו. הסדרה מתחילה מ-0.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144

מה המספר החמישי בסדרה?

fibonaci(4)

• העברנו 4 כפרמטר כי מחשבים מתחילים לספור מ-0.

התוצאה:

3

בחנתי את התארכות משך הריצה של הרצת הפונקציה כנגד סדרה של מספרים מ-2 עד 34 (כי מעבר לזה המחשב שלי קרס), וזו התוצאה:

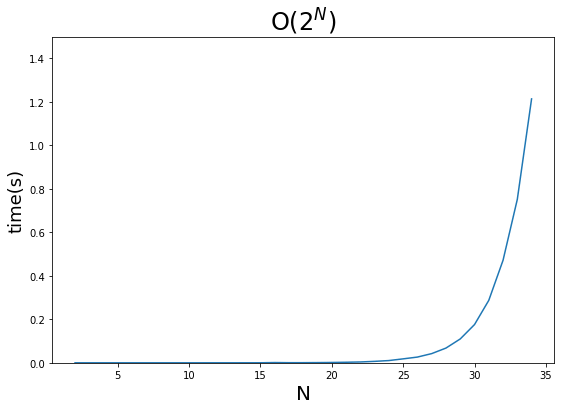
זמן הריצה גדל באופן אקספוננציאלי - הוא מתחיל מאוד רדוד, ואז עולה כמו מטאור. הדרך לתאר את זה היא באמצעות ביטוי big-O שהוא O(2^N), ואם זה הביטוי שמתאר את הקוד שלך אז תכתוב אותו מחדש.

אלגוריתמים גרועים עוד יותר מתאפיינים בקצב גידול פקטוריאלי O(N!) בגלל שהם מחשבים את כל הקומבינציות של רשימה. ואם אמרנו שקצב גידול אקספוננציאלי הוא משהו שצריך להימנע ממנו אז קצב פקטוריאלי הוא גרוע אפילו יותר.

חישוב big-O עבור מקרים מורכבים

עד כה ראינו פונקציות שיש בהם פעולה אחת אבל מה קורה כשיש יותר.

לדוגמה, פונקציה שמציבה 1 לפריט הראשון ברשימה:

def assign_one(numbers):
    list[0] = 1

הפונקציה שייכת לסוג O(1) בגלל שמשך הריצה שלה נותר קבוע ללא תלות במספר הפריטים שמזינים לתוכה.

אבל מה לגבי פונקציה שמציבה 1 לפריט הראשון וגם לפריט השני?

def assign_ones(numbers):
    list[0] = 1
    list[1] = 1

במקום פעולה 1 הפונקציה מבצעת 2.

במקרה שהפונקציה מבצעת מספר פעולות נפרק אותה לפעולות פרטניות, ונחשב עבור כל אחת מהם את ה-big-O:

• הפעולה הראשונה היא O(1)
• גם הפעולה השנייה היא O(1)

סכום ה-big-O של שתי הפעולות הוא 2.

אותנו מעניין ה-N ומהקבוע (2 במקרה זה) אנחנו יכולים להתעלם.

לכן ה-big-O הוא O(1)

למה אנחנו יכולים להתעלם מהקבוע? כי המטרה של big-O היא להבין איך הקוד יתמודד עם רשימות ארוכות במיוחד. וכאשר הרשימה מאוד ארוכה ההבדל בין N לבין 2N הוא זניח. אפשר לחשוב על זה שאין הבדל בין אינסוף לבין פעמיים אינסוף בכל מקרה מדובר במספר מאוד גדול.

נראה דוגמה נוספת לפונקציה מורכבת:

 def do_stuff(array):
     array[0] = 1

     array_len = len(array)

     sum = 0
     for item in array:
          sum += item

     for  item in array:
         sum += item

    return sum

הפונקציה מורכבת מארבע פעולות. נמצא את ה-big-O של כל אחת מהן:

• הצבה של 1 לפריט הראשון של הרשימה - O(1)
• חישוב האורך של רשימה - O(1)
• סכימה של כל פריטי הרשימה בתוך לולאה - O(N)
• סכימה בתוך לולאה פעם שנייה - O(N)

נסכום את ה big-O של הפעולות:

1 + 1 + N + N

אפשר לפשט את הביטוי:

2 * 1 + 2 * N

נסיר את הקבועים כי עבור כמות נתונים מאוד גדולה הם לא משנים:

1 + N

נמצא את הביטוי בעל הסדר הגבוה, ונזניח את כל היתר, כי עבור כמות נתונים גדולה תרומת הפעולות מסדר הגודל הנמוך הופכת זניחה:

N

נשתמש בביטוי בעל הסדר הגבוה בתור ה- big-O:

O(N)

את הפעולות שעשינו כדי למצוא את big-O ניתן לסכם באמצעות אלגוריתם הכולל 5 צעדים:

1. נחלק את הפונקציה למספר פעולות.
2. נמצא את ה big-O של כל פעולה.
3. נסכום את ה big-O של הפעולות השונות.
4. נסיר את הקבועים.
5. נשאיר את הביטוי שהסדר שלו הוא הגבוה ביותר, ונזנח את כל היתר.

סיכום

במדריך זה ראינו מספר אופנים נפוצים לתיאור התארכות משך הזמן של ביצוע משימה ביחס לגידול כמות המידע בו מזינים את התהליך המתוארים באמצעות big-O. הבנת הנושא ויישומו יכולה להיות כל ההבדל בין פונקציה שמשך הריצה שלה סביר ובין קוד אשר גורם לקריסת מערכות. עבור כמות גדולה של נתונים נעדיף אלגוריתם לוגריתמי, ומצד שני נימנע מפונקציות פולינימיות או אקספוננציאליות.

להורדת הקוד עליו מבוסס מדריך big-O

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים