חידה תכנותית: תת מערך בעל סכום מירבי

אתגר: מערך מקסימלי

תיאור הבעיה: בהינתן מערך של מספרים שלמים `nums`, עליך למצוא תת מערך רציף שסכום פריטיו הוא הגבוה ביותר.

לדוגמה, בהינתן המערך הבא:

[2, -4, 1, 2, -2]

הערך שהפונקציה תחזיר צריך להיות 3 כי תת המערך הרציף שסכום איבריו הוא הגבוה ביותר הוא:

[1, 2]

פתרון brute force

הפתרון הפשוט ביותר הוא brute force הבודק כל תת מערך אפשרי במערך הקלט. הפתרון משתמש בלולאה מקוננת ובמשתנה סכום מקסימלי גלובלי. הלולאה החיצונית מתקדמת בכל פעם באלמנט אחד של מערך הקלט ויוצרת מערך מקומי הקצר בפריט אחד. הלולאה הפנימית מחשבת את הסכום המקסימלי של המערך המקומי. אם הסכום המקסימלי של המערך המקומי גבוה מהסכום המקסימלי הגלובלי אז מעדכנים אותו.

ניתן לקוד לדבר:

# The function takes an array of integers as input 
# and returns the maximum sum of subarray in the input array.
def max_subarray_sum(nums): 
    # Variable to store the maximum sum.
    global_max = -float("inf") 

    for idx in range(len(nums)):
        # Variable to store the sum of the current subarray.
        current_sum = 0 
        # Array containing the remaining elements in the array, 
        # starting at the current index.
        local_sub_array = nums[idx:] 
        for num in local_sub_array:
            # Add the current element to the current subarray sum.
            current_sum += num 
            # If the current subarray sum is greater than the global_max, 
            # update the global_max.
            if current_sum > global_max: 
                global_max = current_sum

    return global_max

נבדוק:

# Test cases
print(max_subarray_sum([2, -4, 1, 2, -2]))  # 3
print(max_subarray_sum([1, 2, 3, 4]))  # 10
print(max_subarray_sum([-1, -2, -3]))  # -1
print(max_subarray_sum([-2, -1, -3]))  # -1
print(max_subarray_sum([1]))  # 1
print(max_subarray_sum([-2, 1, 4, -3, 3, 2, -1]))  # 7

האיור הבא מדגים מה קורה בשלבים הראשונים של ריצת הלולאה המקוננת:

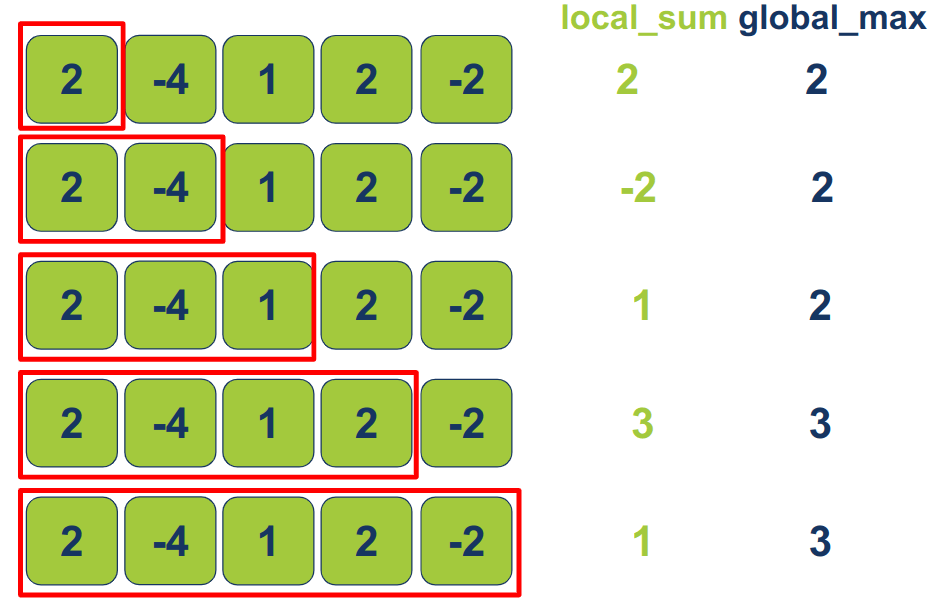
• מתחילים מתת מערך הכולל רק את האיבר הראשון וממנו מחשבים את ה-`local_sum` וה-`global_sum`. בריצה הבאה של הלולאה הפנימית, מרחיבים את תת המערך לשני פריטים. אח"כ לשלושה פריטים, ארבעה, וכיו"ב, עד שהלולאה הפנימית מגיעה לסוף המערך. בכל ריצה של הלולאה הפנימית מעדכנים את ה-`local_sum`, ואם ה-`local_sum` גדול מ-`global_max` אז מעדכנים את הסכום הגלובלי המקסימלי.

בפעם השנייה הלולאה החיצונית מתקדמת בפריט אחד. בהתאם הלולאה הפנימית מתחילה לרוץ מהאיבר השני של המערך:

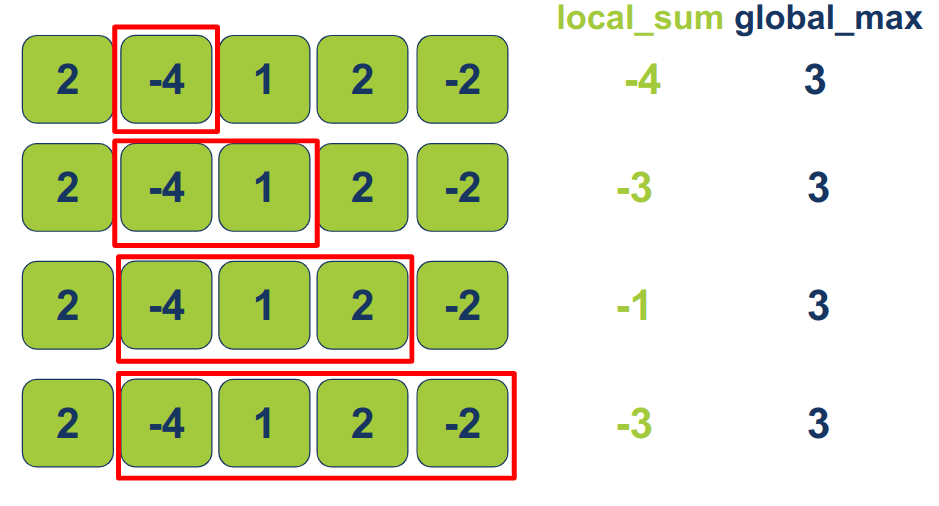
• בכל פעם שהלולאה הפנימית רצה תת המערך המקומי מתארך בפריט אחד נוסף. מתת המערך המקומי מחשבים את ה-`local_sum`, ואם ה-`local_sum` גדול מ-`global_max` מעדכנים את הסכום הגלובלי.

בפעם השלישית הלולאה החיצונית מתקדמת בפריט אחד, ואז הלולאה הפנימית מתחילה לרוץ מהאיבר השלישי של המערך.

בכל פעם שהלולאה החיצונית רצה מתקצר המערך עליו היא רצה בפריט אחד עד שבסופו של דבר ללולאה החיצונית לא נותרים פריטים לעבור עליהם, ואז הפונקציה מסיימת ומחזירה את התוצאה.

הפתרון מתאפיין בסיבוכיות זמן O(N^2) וסיבוכיות מקום O(N):

• הפתרון משתמש בשתי לולאות מקוננות. הלולאה החיצונית מתקדמת בכל פעם בפריט אחד במערך המקור. הלולאה הפנימית רצה על מערך מקומי המתקצר בפריט אחד בכל ריצה של הלולאה החיצונית. המשמעות היא שמספר הפעולות הכולל של הלולאות הוא O(N^2).
• סיבוכיות המקום היא O(N) כאשר התורם העיקרי הוא המערך `local_sub_array` אשר מאחסן מערך חדש בכל ריצה של הלולאה.

מציאת תת המערך הרציף שסכום פריטיו הוא הגבוה ביותר באמצעות אלגוריתם Kadane

אף שקל לחשוב על פתרון brute force קיימת דרך יעילה יותר לפתור את הבעיה והיא משתמשת באלגוריתם Kadane.

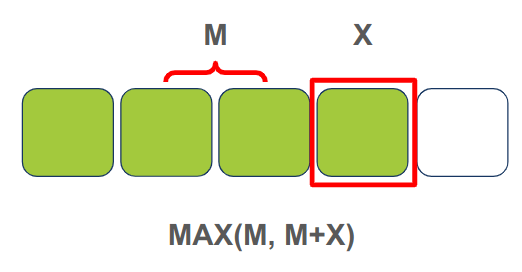
אלגוריתם Kadane מוצא את תת המערך שסכומו הוא הגבוה ביותר.ביישום של האלגוריתם המשתנה `global_max` הוא סכום תת המערך הגבוה ביותר. האלגוריתם עובר פעם אחת על המערך מתחילתו ועד סופו, ועבור כל פריט הוא מוצא את הערך המקסימלי המקומי `current_sum` על ידי השוואת חיבור סכום תת המערך המסתיים בפריט שלפני הנוכחי (M באיור) עם הפריט הנוכחי (M+X) עם הפריט הנוכחי X, ולקיחת הערך הגבוה מבין השניים. אם הגבוה מבין השניים הוא M+X אז הוא מרחיב את תת המערך, ואם X אז הוא מתחיל תת מערך חדש ב-X. אם הערך של `current_sum` גבוה מ-`global_max` אז מעדכנים את `global_max`.

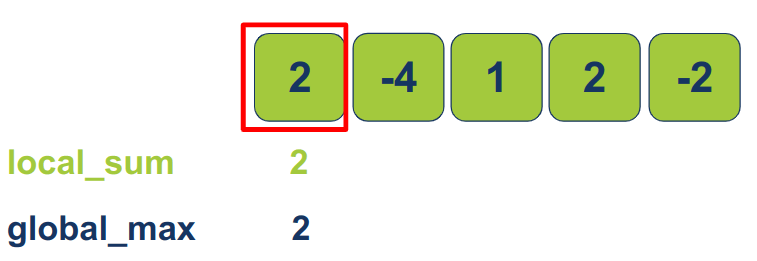
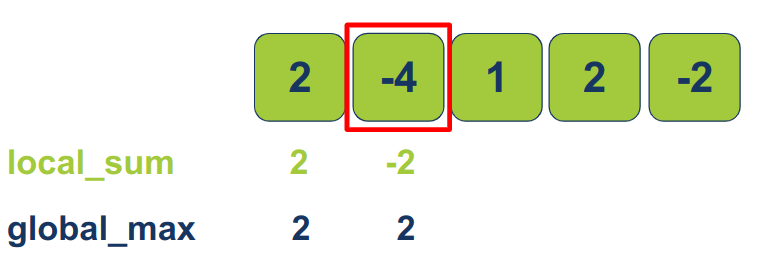
עבור הפריט הראשון המקסימום הגלובלי והמקומי הוא 2 כי זה ערך הפריט הראשון.

עבור הפריט השני המקסימום המקומי הוא ערך הפריט הנוכחי (-4) או הערך הנצבר של תת המערך בתוספת הפריט הנוכחי (2+(-4)):

max(-4, 2+(-4)) = -2

• המקסימום המקומי (-2) נמוך מהמקסימום הגלובלי (2) ולפיכך אין צורך לעדכן את המקסימום הגלובלי.

עבור הפריט השלישי המקסימום המקומי הוא ערך הפריט השלישי (1) או הערך הנצבר של תת המערך בתוספת הפריט הנוכחי (1+(-2)):

max(1, 1+(-2)) = 1

• המקסימום המקומי (1) נמוך מהמקסימום הגלובלי (2) ולכן אין צורך לעדכן את המקסימום הגלובלי.

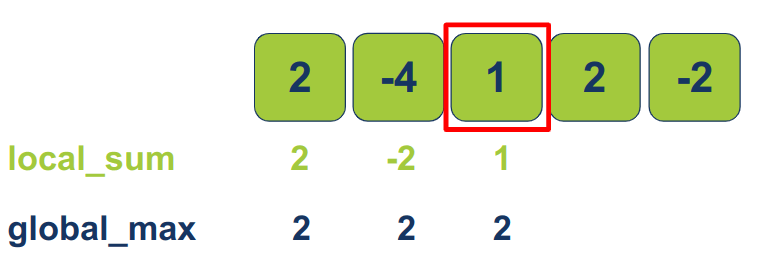
עבור הפריט הרביעי המקסימום הוא ערך הפריט הרביעי (2) או הערך הנצבר של תת המערך בתוספת הפריט הנוכחי (2+1):

max(2, 1+2) = 3

• המקסימום המקומי (3) גבוה מהמקסימום הגלובלי (2) ולכן נעדכן את ערך המקסימום הגלובלי.

עבור הפריט החמישי המקסימום הוא ערך הפריט החמישי (-2) או הערך הנצבר של תת המערך בתוספת הפריט הנוכחי (-2+3):

max(-2, (-2+3)) = 1

• המקסימום המקומי (1) נמוך מהמקסימום הגלובלי (3) ולכן אין צורך לעדכן את המקסימום הגלובלי.

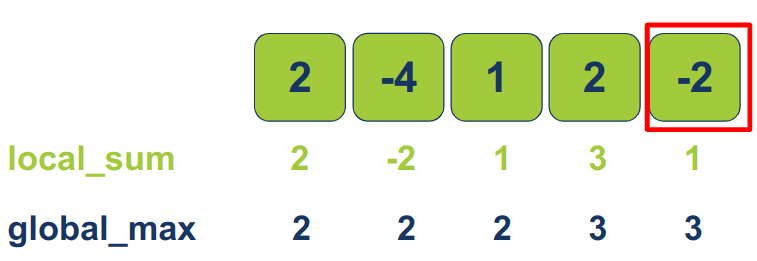
אחרי שעברנו פעם אחת בלבד על המערך באמצעות אלגוריתם Kadane קיבלנו את התשובה שהמקסימום הגלובלי הוא 3.

הקוד הבא מיישם את אלגוריתם Kadane למציאת סכום תת המערך הגבוה ביותר:

def max_subarray_sum(nums):
    if not nums:
        return None

    # Initialize the global maximum and current sum to the value of the first array element
    global_max = nums[0] 
    current_sum = nums[0] 

    len_nums = len(nums)
    for idx in range(1, len_nums):
        num = nums[idx]

        # Update the current sum by taking the maximum between the current 
        # element and the sum of the current element when added to the current sum
        current_sum = max(num, num + current_sum)
        
        # Update the global maximum by taking the maximum between 
        # the global maximum and the current maximum
        global_max = max(global_max, current_sum)


    return global_max

נבדוק:

# Test cases
test_cases = [
              [[-2, 1, -3, 4, -1, 2, 1, -5, 4], 6],
              [[-2, -3, 4, -1, -2, 1, 5, -3], 7],
              [[5,4,-1,7,8], 23],
              [[1], 1],
              [[-1, -2, -3], -1],  # Edge case: all negative numbers
              [[0, 0, 0], 0],  # Edge case: all zeroes
            ]
for nums, expected in test_cases:
    res = max_subarray_sum(nums)
    conclusion = "😄" if res == expected else "😭"
    sign = "==" if res == expected else "!="
    print(f"{conclusion} | {res} {sign} {expected}")

הפונקציה max_subarray_sum() לוקחת מערך של מספרים שלמים כקלט ומחזירה את הסכום המקסימלי של תת מערך רצוף שהוא חלק ממערך הקלט.

הפונקציה פועלת באופן הבא:

1. תחילה היא בודקת אם מערך הקלט ריק. אם זה המצב, הפונקציה מחזירה None.

2. אחרת, הפונקציה מאתחלת שני משתנים: `global_max` ו-`current_sum` שערכם ההתחלתי שווה לפריט הראשון (אינדקס 0) במערך הקלט:

   • `global_max` - יאחסן את הסכום המקסימלי שנמצא עד כה, וזה גם מה שהפונקציה תחזיר.

   • `current_sum` יאחסן את הסכום של תת המערך הנוכחי.

3. הפונקציה עוברת על מערך הקלט, החל מאינדקס 1. עבור כל אינדקס במערך, הפונקציה עושה את הדברים הבאים:

   • מעדכנת את `current_sum` על ידי מציאת הערך הגבוה בין שניים: פריט המערך הנוכחי אל מול תוספת הפריט הנוכחי לסכום תת המערך הרציף הנצבר.

   • מעדכנת את `global_max` על ידי מציאת המקסימום בין `global_max` ו-`current_sum`.

4. לאחר מעבר על המערך כולו, הפונקציה מחזירה את `global_max`.

הפונקציה יעילה מאוד הודות לסיבוכיות זמן של O(N) כאשר N הוא אורך מערך הקלט וסיבוכיות מקום קבועה O(1).

אלגוריתם Kadane מציג גישה פשוטה וחכמה לפתרון בעיית "המערך המקסימלי". הוא מזהה ביעילות את המערך שיש לו את הרצף עם הסכום המקסימלי בזמן שהוא עובר רק פעם אחת על מערך הקלט, תוך קבלת החלטות המבוססות על המקסימום המקומי. כאשר נמצא מערך רציף חדש עם מקסימום מקומי גבוה יותר, הוא מעדכן את המקסימום המקומי, ואם המקסימום המקומי גבוה יותר מהמקסימום הגלובלי, הוא מעדכן את המקסימום הגלובלי. גישה זו מאפשרת לאלגוריתם להחזיר את המקסימום הגלובלי בתור תשובה לבעייה.

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

חידה תכנותית: twoSum

טכניקת חלון ההזזה sliding window לפתרון בעיות ברצפים

פתרון בעיות אופטימיזיציה באמצעות אלגוריתם חמדן

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים