טכניקת חלון ההזזה sliding window לפתרון בעיות ברצפים
אתגר: מציאת תת מערך שסכום הפריטים שלו מקסימלי
נתון מערך array של מספרים שלמים ומספר k, ועליך למצוא תת מערך רציף באורך k שאם תחבר את הפריטים המרכיבים אותו ייתן סכום מקסימלי.
לדוגמה: בהינתן מערך [2, 3, 1, 5, 6, -1] ו k=3, תת המערך הרציף שסכום איבריו מקסימלי הוא [1, 5, 6].
את הבעיה נפתור בשתי גישות:
- גישת brute force שבוחנת את כל הצירופים האפשריים ובוחרת את המתאים ביותר
- שימוש בטכניקת sliding window (חלון הזזה) שהיא יעילה הרבה יותר
פתרון brute force
בגישה שהיא brute force נבחן את כל תתי המערכים האפשריים באורך k, נחשב את סכומם, ונבחר את המערך שיש לו את הסכום הגבוה ביותר.
קודם נשרטט את הבעיה כדי שיהיה קל יותר להבין את הפתרון.
נתון מערך:

נסמן תת מערך באורך k = 3 אשר מתחיל מעמדת אינדקס 0:

נציין את הסכום הנוכחי של תת המערך cur_sum ואת הסכום המקסימלי mx_sum שבשלב זה הם שווים:
Sum = 2 + 3 + 1 = 6

נבחן את תת המערך הבא שתחילתו בעמדת אינדקס 1:

Sum = 3 + 1 + 5 = 9
- סכום הפריטים הוא 9 וזה גם הסכום המקסימלי.
נבחן את תת המערך הבא אשר מתחיל בעמדת אינדקס 2:

- סכום הפריטים הוא 12 וזה גם הסכום המקסימלי.
נבחן את תת המערך הבא אשר מתחיל בעמדת אינדקס 4:

- סכום הפריטים הוא 10 ולכן הסכום המקסימלי נשאר ללא שינוי (12).
לאחר שבחנו את כל הקומבינציות של תת המערכים באורך k נסיק שהסכום הגבוה ביותר האפשרי הוא 12.
נקודד את הפתרון בגישה brute force:
def find_max_sub_arr_size_k_brute_force(arr:[], k: int):
# Initialize the maximum sum to negative infinity
max_sum = -float("infinity")
# Get the length of the input array
arr_len = len(arr)
# Iterate through the array
for idx in range(arr_len):
# Create a subarray of size 'k' starting at index 'idx'
sub_arr = arr[idx:idx+k]
# Check if the subarray has the desired size 'k'
if len(sub_arr) == k:
# Initialize a sum for the subarray
sub_arr_sum = 0
# Iterate through the subarray and calculate the sum
for s_idx in range(k):
sub_arr_sum += sub_arr[s_idx]
# Update the maximum sum if the current subarray sum is larger
max_sum = max(sub_arr_sum, max_sum)
# Return the maximum sum found among all subarrays
return max_sum
# Example usage
arr = [2, 3, 1, 5, 6, -1]
k = 3
max_sub_arr = find_max_sub_arr_size_k_brute_force(arr, k)
print(f"The max sub array is `{max_sub_arr}`")
נסביר:
-
הפונקציה find_max_sub_arr_size_k_brute_force משתמשת בטכניקה של לולאה בתוך לולאה כדי למצוא את הסכום הגבוה ביותר של תת המערכים באורך k בתוך מערך arr שהיא מקבלת כפרמטר.
-
המשתנה max_sum עוקב אחר סכום תת המערכים הגבוה ביותר, ו-sub_arr_sum אחר סכום תת המערך הנוכחי.
-
הלולאה החיצונית רצה על כל פריטי המערך (מאינדקס 0 ועד n אורך המערך) ויוצרת תתי מערכים sub_arr באורך k כשבכל פעם האינדקס ממנו מתחיל תת המערך נע מקום אחד לימין:
# Create a subarray of size 'k' starting at index 'idx' sub_arr = arr[idx:idx+k] -
הלולאה הפנימית רצה על תת המערך וסוכמת אותו:
# Initialize a sum for the subarray sub_arr_sum = 0 # Iterate through the subarray and calculate the sum for s_idx in range(k): sub_arr_sum += sub_arr[s_idx] -
בנוסף, הלולאה הפנימית בודקת האם הסכום של תת המערך גבוה יותר מסכום המקסימום ומעדכנת אם צריך:
# Update the maximum sum if the current subarray sum is larger max_sum = max(sub_arr_sum, max_sum)
הגישה של brute force - במקרה שלנו, לולאה בתוך לולאה - היא הכי פשוטה, ולא מצריכה מחשבה עודפת. נותנים למחשב שיעבוד במקומנו.
האם הפתרון brute force הוא היעיל ביותר?
הלולאה החיצונית רצה n פעמים כמספר הפריטים במערך, והלולאה הפנימית רצה בכל פעם k כדי להשלים מעבר על כל פריטי תת המערך הנוכחי מה שנותן ביחד סיבוכיות זמן של :
O(n*k)
האם אנחנו יכולים להשיג את אותה התוצאה ביעילות רבה יותר? מסתבר שכן.
פתרון מבוסס sliding window
טכניקת sliding window "חלון ההזזה" משמשת לפתרון בעיות על מבני נתונים סדרתיים (מחרוזות, מערכים). הרעיון הוא להחזיק "חלון" של פריטים שמזיזים באופן שיטתי לאורך רצף הנתונים, תוך כדי שמבצעים פעולות להשגת הפתרון.
נסביר איך ליישם sliding window לפתרון הבעיה שעל הפרק.
נחזור למערך, ונתחיל מהצבת החלון על אינדקס 0:

נזיז את החלון לעמדת האינדקס 1:

כדי לחשב את סכום תת המערך, במקום להשתמש בלולאה, נפחית את הפריט שלפני העמדה הראשונה של תת המערך (מסומן באפור) ונוסיף את הפריט שהתווסף למערך החדש (מסומן באדום):

נחשב: יש לנו סכום של 6 מהחלון הקודם ועכשיו זזנו עמדת אינדקס אחת אז נפחית את הפריט שיצא מחוץ למסגרת שערכו 2 ונקבל 4, ונוסיף את הפריט שנוסף למסגרת שערכו 5 ונקבל שסכום תת המערך הוא 9 ומכיוון ש-9 גבוה יותר מהסכום המקסימלי נעדכן גם את הסכום המקסימלי.

נחזור על התהליך הכולל את:
- קידום החלון בעמדת אינדקס אחת לימין
- הסרת הפריט שיצא מחוץ למסגרת מהסכום הנוכחי
- הוספת הפריט שנוסף למסגרת לסכום הנוכחי
- השוואת הסכום הנוכחי לסכום המקסימלי ועדכון הסכום המקסימלי במידת הצורך
עד שנעבור על כל פריטי המערך.
כך זה נראה:

הקוד הבא פותר את האתגר בגישת sliding window:
def find_max_sub_arr_size_k_sliding_window(arr: [], k: int):
# Handle the edge case: If the array is shorter than or equal to k, return the sum of all elements.
if len(arr) <= k:
return sum(arr)
# Calculate the sum of the first k elements to initialize sub_arr_sum and max_sum.
sub_arr_sum = max_sum = sum(arr[:k])
# Iterate through the array using a sliding window approach.
for idx in range(len(arr) - k):
# Subtract the element that's moving out of the window and add the element entering the window.
sub_arr_sum = sub_arr_sum - arr[idx] + arr[idx + k]
# Update max_sum if the current subarray sum is greater.
max_sum = max(max_sum, sub_arr_sum)
return max_sum
# Test case
arr = [2, 1, 5, 4, -3, 2]
k = 3
max_sub_arr = find_max_sub_arr_size_k_sliding_window(arr, k)
print(f"The max subarray sum of size {k} is {max_sub_arr}")
נסביר:
-
טיפול במקרה הקצה:
if len(arr) <= k: return sum(arr)-
בודק אם אורך מערך הקלט arr קטן או שווה ל- k, שהוא גודל תת-המערך שאנו רוצים למצוא את הסכום המרבי שלו. אם המערך קצר יותר או שווה ל- k, אין צורך להמשיך והקוד פשוט מחזיר את סכום כל הפריטים במערך, מכיוון שאי אפשר ליצור תת-מערך בגודל k.
-
-
אתחול המשתנים sub_arr_sum ו-max_sum:
sub_arr_sum = max_sum = sum(arr[:k])sub_arr_sum ו-max_sum מאותחלים כסכום k הפריטים הראשונים של מערך הקלט המהווים את תת-המערך הראשון באורך k.
-
מעבירים חלון הזזה sliding window על ידי הפעלת לולאה על המערך:
for idx in range(len(arr) - k):הלולאה תרוץ len(arr) - k - 1 פעמים, וזה גם יהיה מספר תת המערכים הנבחנים.
-
בתוך הלולאה מעדכנים את סכום תת המערך על ידי החסרת האלמנט שיוצא מהמסגרת והוספת האלמנט שנוסף למסגרת:
sub_arr_sum = sub_arr_sum - arr[idx] + arr[idx + k] -
נעדכן את הmax_sum:
max_sum = max(max_sum, sub_arr_sum) -
לאחר עדכון sub_arr_sum, אנו משווים אותו ל- max_sum הנוכחי ומעדכנים את max_sum לגדול מביניהם. זה מבטיח ש- max_sum יהיה תמיד הסכום המרבי שנמצא בין התת-מערכים שנבדקו עד כה.
-
לבסוף, הפונקציה מחזירה את max_sum, המייצג את הסכום המרבי של תת-מערך בגודל k בתוך המערך הקלט.
יעילות הפתרון המבוסס על sliding window:
הלולאה עוברת על כל פריט מערך בדיוק פעם אחת כאשר בתוך הלולאה מתבצעות פעולות בזמן קבוע (דוגמת, הוספה והחסרה). בהנחה שאורך המערך הוא n סיבוכיות הזמן של הפתרון היא קווית O(n), תלויה באופן לינארי באורך המערך.
כמות הזכרון הדרושה לביצוע הקוד תלויה המשתנים, כולם דורשים מקום קבוע ולפיכך סיבוכיות המקום היא קבועה O(1).
השוואה בין פתרונות brute force ו- sliding window
בעוד יותר קל להגות ולכתוב פתרון שהוא brute force הקומפלקסיות של משך ביצוע הפתרון היא O(n*k) שהיא גרועה משמעותית מאשר משך ביצוע O(n) כשמשתמשים בטכניקה של sliding window. כל עוד עובדים על דוגמאות פשוטות ומועטות פריטים אין לזה חשיבות אבל ככל שעוברים למערכות מורכבות עם מספר פריטים רב יותר ההבדל הופך למשמעותי יותר. אם משהו לא ברור אז אתה חייב לעצור עכשיו כי כתיבת קוד יעיל היא ההבדל בין כתיבת אפליקציה לבין אפליקציה עובדת. כדי להבין את הנושא יותר לעומק כדאי לקרוא את המדריךbig-O ביטוי ליעילות הקוד.
מהי טכניקת "חלון הזזה" sliding window לפתרון בעיות תכנותיות?
הטכניקה של sliding window חלון הזזה היא שימושית במיוחד לפתור בעיות הכוללות מערכים, מחרוזות או מבני נתונים סדרתיים אחרים. הרעיון הבסיסי של טכניקת ה-sliding window הוא לשמור על "חלון" של פריטים כאשר עוברים על הנתונים באופן סדרתי, ולבצע פעולות על פריטי החלון במטרה לפתור את הבעיה שמעוניינים לפתור.
יישום טכניקת ה-sliding window כולל:
- הגדרת החלון: תחילה, מגדירים חלון בגודל קבוע. החלון הזה ינוע או יעבור על מבנה הנתונים באופן סדרתי.
- עיבוד ראשוני של החלון: יש למלא את החלון עם הפריטים הראשונים של מבנה הנתונים.
- מעבר בתוך לולאה ועדכון: הלולאה מקדמת את החלון באלמנט אחד בכל פעם. בתוך החלון מתבצעת עבודה על החלון. זה יכול להיות השוואה, הוספה או החסרה. תלוי מה שדורשת הבעיה שעל הפרק.
- עדכון הפתרון: בכל שלב, אתה יכול לחשב או לעדכן ערך כלשהו בהתאם לפריטים הקיימים בחלון. הערך תלוי בשאלה, ויכול להיות: סכום, ממוצע, מקסימום, מינימום או כל מדד רלוונטי אחר.
- התאמת החלון: בהתאם לבעיה, ייתכן שיהיה עליך להתאים את גודל החלון באופן דינמי. זה יכול לכלול הרחבה או הקטנת החלון ככל שאתה עובר דרך הנתונים.
טכניקת ה-sliding window משמשת לעתים קרובות כדי לייעל את פתרון של בעיות שונות, דוגמת:
- בעיות תת-מערך: מציאת תת-מערך שיש לו סכום מקסימלי או מינימלי או שווה לערך מסויים.
- בעיות מחרוזת: חיפוש תת מחרוזת המצייתת לדפוס נתון בתוך מחרוזת גדולה יותר.
- בעיות של שני מצביעים: פתרון בעיות שבהן אתה שומר על שני מצביעים או אינדקסים ש"נעים" דרך הנתונים, כגון מציאת זוגות שסכומם שווה לערך רצוי.
יתרונה המרכזי של טכניקת ה-sliding window חלון ההזזה טמון ביכולתה לפתור בעיות בזמן ליניארי או כמעט ליניארי O(n) תוך שימוש יעיל בזיכרון, לעיתים קרובות O(1).
אתגר: הזמן הטוב ביותר לקנות ולמכור מניות
נתון מערך מחירים שבו prices[i] הוא מחיר של מניה ביום i. אתה רוצה למקסם את הרווח שלך על ידי בחירת יום יחיד לקנות בו מניה אחת ובחירת יום אחר בעתיד למכור את המניה. עליך לכתוב פונקציה המחזירה את הרווח המרבי שאתה יכול להשיג מעסקה זו. אם אינך יכול להשיג רווח כלשהו, הפונקציה תחזיר 0.
לדוגמה, נתון המערך:
[8, 2, 6, 4, 7, 5]
הרווח המרבי הוא 5, מכיוון שאפשר לקנות את המניה ביום 2 (מחיר = 2) ולמכור אותה ביום 5 (מחיר = 7).
אתה צריך ליישם פונקציה:
pick_when_to_buy_and_sell(prices: List[int])
המקבלת מערך של מחירי מניות ומחזירה את הרווח המרבי אותו ניתן לקבל, ואת הימים בהם כדאי לקנות ולמכור.
לפני שנפתור את האתגר באמצעות קוד, נשרטט את הנתונים כדי להמחיש במה מדובר. נצייר מטריצה שציר ה-Y הוא המחירים וציר ה-X הוא הימים, ונוסיף את הנקודות:

בין היום הראשון השני לשני אפשר לראות ירידה מ-8 ל-2. על יום הרכישה נשים מצביע buy ועל יום המכירה יצביע sell:

מה שאומר שהרווח הוא 6- והרווח המקסימלי הוא 0 (לפי תנאי הבעיה אי אפשר להחזיר ערך שלילי).
- פה אני קורא למצביעים buy ו-sell. המצביע buy יקדים תמיד את sell. לכן, על הציר האופקי buy ימצא משמאל ל-sell.
- לצורך הפתרון אנחנו משתמשים בטכניקה של שני מצביעים כפי שהסברתי במדריך שימוש בשני מצביעים לפתרון בעיות תכנותיות.
מכיוון שלא כדאי לרכוש ביום ראשון נעביר את יום הרכישה לשני ונקדם את יום המכירה באינדקס 1 כי המכירה צריכה להיות רק אחרי הרכישה:

- אם נרכוש ביום השני במחיר 2, ונמכור ביום השלישי במחיר 6 הרווח יהיה 4 וזה גם יהיה הרווח המקסימלי.
נמשיך לחפש הזדמנות להגדלת הרווח המקסימלי. לשם כך, נקדם את יום המכירה משלישי לרביעי, מה שיגרום לירידה במחיר המכירה, ולפיכך הרווח המקומי יהיה `4 - 2 = 2` . שאינו גבוה מהרווח המקסימלי ועל כן נמנע מעדכון הרווח המקסימלי:

נמשיך לחפש הזדמנות להגדלת הרווח. לשם כך, נקדם את יום המכירה מרביעי לחמישי, מה שיגרום לעלייה במחיר המכירה, ולפיכך הרווח המקומי יהיה `7 - 2 = 5` הגבוה מהרווח המקסימלי. בהתאם נעדכן את הרווח המקסימלי:

נמשיך לחפש הזדמנות להגדלת הרווח. לשם כך, נקדם את יום המכירה מחמישי לשישי, מה שיגרום לירידה במחיר המכירה, ולפיכך הרווח המקומי יהיה `5 - 2 = 3` הנמוך מהרווח המקסימלי, ולפיכך אין צורך לעדכן את הרווח המקסימלי.
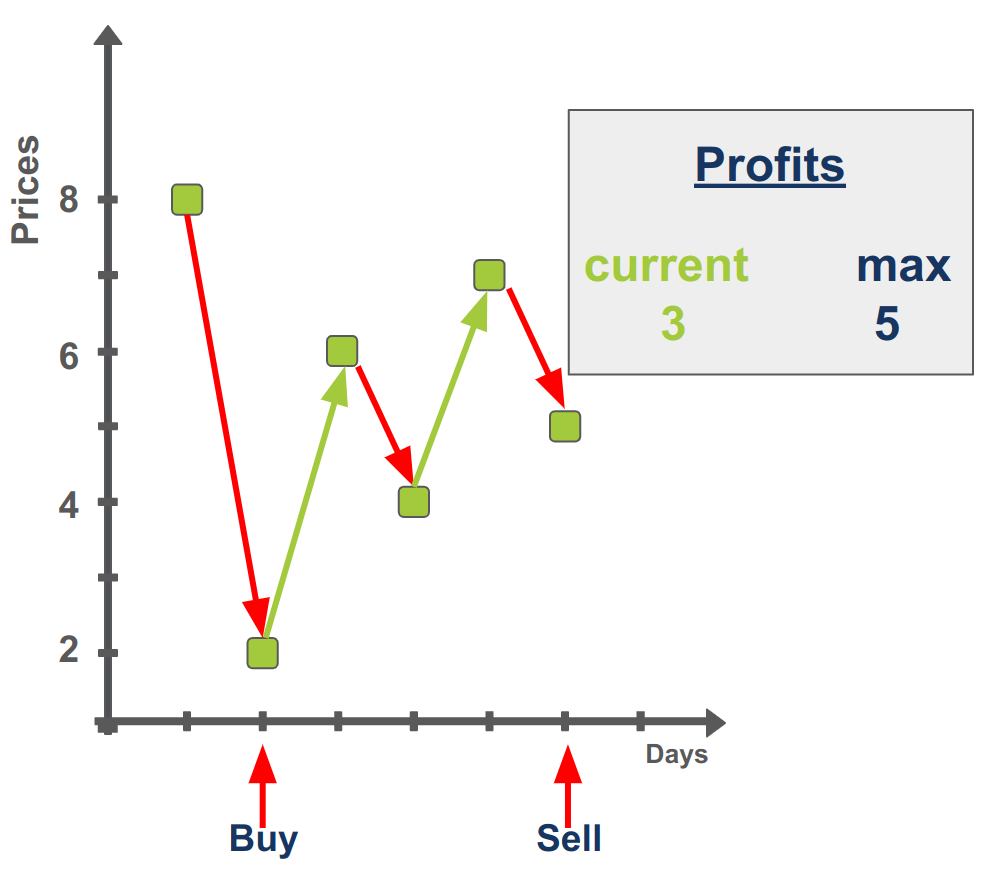
המסקנה היא שכדי להשיג את הרווח המקסימלי של 5 צריך לרכוש ביום 2 ולמכור ביום 5:

הקוד לבחירת הזמן הטוב ביותר לקנות ולמכור מניות:
def pick_when_to_buy_and_sell(prices: []):
number_of_trading_days = len(prices)
# Check if there are at least 2 trading days, as we can't trade with fewer days.
if number_of_trading_days < 2:
raise Exception("Not enough trading days")
# Initialize buy pointer to day 0 and sell pointer to day 1
buy_day = 0
sell_day = 1
# Initialize the maximum profit to 0; our goal is to maximize this profit.
max_profit = 0
# Track the buy and sell days that generate the maximum profit.
max_profit_buy_day = buy_day
max_profit_sell_day = sell_day
# Iterate through the trading days.
while sell_day < number_of_trading_days:
# Calculate the current profit from buying on buy day and selling on sell day.
current_profit = prices[sell_day] - prices[buy_day]
# If the current trade is not profitable, move the buy day to the sell day, as it's the lowest price.
if current_profit < 0:
# If current trade isn't profitable move the buy day to the sell day cause the sell day is the lowest
buy_day = sell_day
else:
# Update max_profit, buy and sell days if a new maximum profit is found.
if current_profit > max_profit:
max_profit = current_profit
max_profit_buy_day = buy_day
max_profit_sell_day = sell_day
# Advance the sell day to explore more possibilities for gaining profit.
sell_day += 1
# If no profits can be obtained, return 0.
if max_profit < 0:
return 0
return max_profit_buy_day, max_profit_sell_day, max_profit
# Test cases
def call_pick_when_to_buy_and_sell(prices):
ret = f"Given prices {prices}"
try:
buy_day, sell_day, max_profit = pick_when_to_buy_and_sell(prices)
if max_profit < 1:
ret += " -> No profits can be obtained"
else:
ret += f" -> The max profit of {max_profit} is obtained when buying on day {buy_day} and selling on day {sell_day}"
except Exception as e:
print(e)
return ret
test_cases = [
[1, 7, 5, 3, 6, 8], # Buying on day 0 and selling on the last day,
[0, 8, 5, 4], # Buy and sell on the first 2 days
[4, 5, 0, 8], # Buy and sell on the last 2 days
[2, 1, 5, 3, 8, 5], # Buying and selling in between the first and last days
[5, 2, 1, 0], # Can't make a profit
[3, 4], # 2 items
[3, 3], # Can't make a profit
[4, 3], # Can't make a profit
[1] # Not enough trading days
]
for prices in test_cases:
print(call_pick_when_to_buy_and_sell(prices))
נסביר את הפונקציה pick_when_to_buy_and_sell():
-
number_of_trading_days = len(prices)-
הפונקציה מתחילה מחישוב מספר ימי המסחר הכולל ע"פ אורך המערך prices.
-
-
if number_of_trading_days < 2: raise Exception("Not enough trading days")-
הפונקציה בודקת את מקרה הקצה בו ישנם פחות מ-2 ימי מסחר, במצב זה לא ניתן לסחור והפונקציה זורקת Exception.
-
-
buy_day = 0 sell_day = 1-
מאתחל שני מצביעים: buy_day מייצג את היום של קניית המניה, ו-sell_day מייצג את יום המכירה. הם מתחילים בימים הראשון והשני, בהתאמה (אינדקס 0 ו- 1).
max_profit = 0-
משתנה max_profit מייצג את הרווח המקסימלי הוא מאותחל ל-0, והמטרה שלנו היא למקסם אותו.
-
-
max_profit_buy_day = buy_day max_profit_sell_day = sell_day-
משתנים העוקבים אחר ימי הקנייה והמכירה שיוצרים את הרווח המרבי. הם מאותחלים עם הערכים הראשוניים של buy_day ו-sell_day.
-
-
את עיקר העבודה עושה הלולאה:
while sell_day < number_of_trading_days:אשר רצה מיום המסחר הראשון לאחרון.
-
בתוך הלולאה מחושב הרווח הנוכחי על סמך מהפחתת מחיר המנייה ביום הרכישה מהמחיר ביום המכירה:
current_profit = prices[sell_day] - prices[buy_day] -
אם המסחר הנוכחי אינו רווחי (כלומר, current_profit < 0), פירוש הדבר שרכישה ב-buy_day הנוכחי ומכירה ב-sell_day הנוכחי תגרום להפסד. במקרה זה, הקוד מעדכן את buy_day ל-sell_day הנוכחי מכיוון שהוא נחשב למחיר הנמוך ביותר לקנייה:
if current_profit < 0: buy_day = sell_day -
אם הרווח הנוכחי עוקף את הרווח המקסימלי עד כה (כלומר, current_profit > max_profit), הקוד מעדכן את הרווח המקסימלי ברווח הנוכחי וגם מעדכן את הימים בהם הכי כדאי למכור ולקנות מכיוון שימים אלה מייצגים את הזמן הטוב ביותר לקנות ולמכור כדי למקסם את הרווח:
if current_profit > max_profit: max_profit = current_profit max_profit_buy_day = buy_day max_profit_sell_day = sell_day -
לבסוף, הלולאה מקדמת את sell_day בעמדת אינדקס אחת כדי לחקור אפשרויות נוספות להשגת רווח באיטרציה הבאה של הלולאה:
sell_day+=1
-
-
לאחר שהלולאה מסיימת לרוץ, אם לא ניתן לקבל רווחים (כלומר, max_profit < 0), הקוד מחזיר 0 מכיוון שאי אפשר להרוויח.
הערכת ביצועים של הזמן הטוב ביותר לקנות ולמכור:
סיבוכיות הזמן היא O(n) הנובעת משימוש בטכניקת שני המצביעים המאפשרת לעבור בלולאה פעם אחת על כל ימי המסחר. הפונקציה מכילה משתנים הדורשים מקום קבוע בזיכרון, ועל כן סיבוכיות המקום היא O(1). השילוב של סיבוכיות זמן O(n) וסיבוכיות מקום O(1) מבטיחים את יעילות הפונקציה.
אתגר: למצוא את האינדקס בו נמצא ה- 0 שיש להחליפו ב-1 לקבלת תת המערך הארוך ביותר של אחדות
נתון מערך בינארי המכיל את הספרות 1 ו-0 בלבד. המטרה שלך היא למצוא את האינדקס של 0, שאם יוחלף ב-1, יפיק את הרצף ההמשכי הארוך ביותר של אחדות.
לדוגמה, בהינתן המערך הבינארי `[1, 0, 1, 1, 0, 1, 1, 1]`, אתה יכול להחליף את ה-0 בעמדת אינדקס 3 או 6. מבין שתי האפשרויות, החלפת 0 בעמדה 3 תביא לרצף ההמשכי הארוך ביותר של אחדות באורך 6.
המשימה שלך היא ליישם פונקציה :
find_index_to_replace(arr: List[int])
אשר תקבל מערך בינארי ותחזיר את העמדה של 0 אותה יש להחליף כדי לקבל את הרצף הארוך ביותר של אחדות, ואת אורך הרצף המתקבל מההחלפה.
פתרון:
def find_idx_of_0_to_be_replaced_by_1(arr: []):
# Initialize variables
# Max length of contiguous 1s
max_seq_len = 0
# Current length of 1s sequence
current_seq_len = 0
# Track how many flips were performed
count_flips = 0
# Track the last known flipped index
last_known_0_idx = -1
# Track the flipped index in the longest known subarray
flipped_0_idx = -1
# Iterate through the array
for idx, item in enumerate(arr):
# If current item is 1
if item == 1:
# Increment current sequence length of 1s
current_seq_len += 1
if current_seq_len == 1:
# Reset flip count if this is the start of a new sequence of 1s
count_flips = 0
# If current item is 0
elif item == 0:
if count_flips == 1:
# Set current sequence length if it contains a flip
current_seq_len = idx - last_known_0_idx
else:
# Flip the current item and increment current_seq_len
count_flips = 1
current_seq_len += 1
# Update last known 0 index
last_known_0_idx = idx
# Update the maximum sequence length if needed
if current_seq_len > max_seq_len:
max_seq_len = current_seq_len
# Update the flipped index for the longest subarray
flipped_0_idx = last_known_0_idx
return max_seq_len, flipped_0_idx
# Test cases
arrs = [
[0, 1, 0, 1],
[1, 1, 0, 0, 1, 0, 1, 1],
[0, 1, 0, 0, 1, 0, 1, 1],
[0, 1, 0, 0, 1, 0, 1, 1, 0],
[1, 0, 1, 1, 0, 1, 1, 1],
[1, 0, 1, 1, 0, 1, 0, 1],
[0, 0, 0, 0, 0],
[0, 1],
[1, 0],
[0],
[1],
[]
]
for arr in arrs:
seq_len, idx = find_idx_of_0_to_be_replaced_by_1(arr)
print(f"{arr} has a length of {seq_len} consecutive 1s after flipping at index {idx}")
נסביר:
הפונקציה find_idx_of_0_to_be_replaced_by_1() מוצאת את האינדקס של 0 במערך הבינארי, אשר החלפתו ב-1, תיתן את הרצף ההמשכי הארוך ביותר של אחדות. במסגרת הפונקציה:
-
הפונקציה מקבלת מערך בינארי arr כקלט.
-
מספר משתנים מוגדרים כדי לעקוב אחר אורך הרצף המרבי של אחדות (max_seq_len), אורך הרצף הנוכחי של אחדות (current_seq_len), מספר ההיפוכים (count_flips), האינדקס האחרון הידוע של 0 (last_known_0_idx), ואת האינדקס של ה-0 שהוחלף המשתייך לתת המערך הארוך ביותר של אחדות (flipped_0_idx).
-
הפונקציה עוברת על מערך הקלט arr באמצעות לולאת for עם enumerate. זה מאפשר לה לעקוב אחר האינדקס (idx) ואחר הפריט הנוכחי (item) במערך.
-
בתוך הלולאה, ישנן הוראות כיצד לטפל במקרים השונים של אחדות ואפסים במערך:
-
אם הפריט הנוכחי הוא 1, הקוד מגדיל את current_seq_len כדי לספור את האחדות העוקבות ברצף הנוכחי. אם, בנוסף, current_seq_len הוא 1, count_flips יוגדר כ-0 מכיוון שזו ההתחלה של רצף חדש של אחדות.
-
אם הפריט הנוכחי הוא 0, הקוד בודק אם count_flips הוא כבר 1. אם כן, זה אומר שהיה כבר 0 שהוחלף בתת המערך הנוכחי. במקרה זה, הוא קובע את current_seq_len להפרש בין האינדקס הנוכחי (idx) לבין last_known_0_idx. אם count_flips אינו 1, זה אומר שתת המערך הנוכחי אינו מכיל החלפה, כך שניתן להפוך, ולפיכך count_flips עובר ל-1 כדי לציין החלפה וגם צריך להאריך את current_seq_len ב-1. בנוסף, last_known_0_idx מתעדכן עם האינדקס הנוכחי idx .
-
-
לאחר עיבוד הפריט הנוכחי של המערך, הלולאה בודקת אם current_seq_len ארוך יותר מ-max_seq_len. אם כן, הוא מעדכן את max_seq_len עם אורך הרצף המרבי החדש ומעדכן את flipped_0_idx עם last_known_0_idx. זה מבטיח שהפונקציה עוקבת אחר האינדקס של ה-0, אשר החלפתו ב-1, גורמת לתת המערך הארוך ביותר המכיל אחדות.
-
לבסוף, הפונקציה מחזירה tuple המכיל max_seq_len (אורך התת-מערך הארוך ביותר של אחדות) ו-flipped_0_idx (האינדקס של ה-0 שיש להחליף על מנת לקבל את תת המערך הארוך ביותר).
הערכת ביצועים של אתגר מציאת האינדקס בו נמצא 0 שיש להחליפו ב- 1 לקבלת תת המערך הארוך ביותר של אחדות
סיבוכיות הזמן היא O(n) הנובעת משימוש בטכניקת ה-sliding window המאפשרת לעבור בלולאה פעם אחת על כל פריטי המערך. הפונקציה מכילה משתנים הדורשים מקום קבוע בזיכרון, ועל כן סיבוכיות המקום היא O(1). השילוב של סיבוכיות זמן O(n) וסיבוכיות מקום O(1) מבטיחים את יעילות הפונקציה.
מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך
שימוש בטכניקות שני המצביעים לפתרון בעיות תכנותיות
לכל המדריכים בסדרה ללימוד פייתון
אהבתם? לא אהבתם? דרגו!
0 הצבעות, ממוצע 0 מתוך 5 כוכבים


המדריכים באתר עוסקים בנושאי תכנות ופיתוח אישי. הקוד שמוצג משמש להדגמה ולצרכי לימוד. התוכן והקוד המוצגים באתר נבדקו בקפידה ונמצאו תקינים. אבל ייתכן ששימוש במערכות שונות, דוגמת דפדפן או מערכת הפעלה שונה ולאור השינויים הטכנולוגיים התכופים בעולם שבו אנו חיים יגרום לתוצאות שונות מהמצופה. בכל מקרה, אין בעל האתר נושא באחריות לכל שיבוש או שימוש לא אחראי בתכנים הלימודיים באתר.
למרות האמור לעיל, ומתוך רצון טוב, אם נתקלת בקשיים ביישום הקוד באתר מפאת מה שנראה לך כשגיאה או כחוסר עקביות נא להשאיר תגובה עם פירוט הבעיה באזור התגובות בתחתית המדריכים. זה יכול לעזור למשתמשים אחרים שנתקלו באותה בעיה ואם אני רואה שהבעיה עקרונית אני עשוי לערוך התאמה במדריך או להסיר אותו כדי להימנע מהטעיית הציבור.
שימו לב! הסקריפטים במדריכים מיועדים למטרות לימוד בלבד. כשאתם עובדים על הפרויקטים שלכם אתם צריכים להשתמש בספריות וסביבות פיתוח מוכחות, מהירות ובטוחות.
המשתמש באתר צריך להיות מודע לכך שאם וכאשר הוא מפתח קוד בשביל פרויקט הוא חייב לשים לב ולהשתמש בסביבת הפיתוח המתאימה ביותר, הבטוחה ביותר, היעילה ביותר וכמובן שהוא צריך לבדוק את הקוד בהיבטים של יעילות ואבטחה. מי אמר שלהיות מפתח זו עבודה קלה ?
השימוש שלך באתר מהווה ראייה להסכמתך עם הכללים והתקנות שנוסחו בהסכם תנאי השימוש.