מבחן ANOVA - האם ממוצעי קבוצות שונים סטטיסטית

במדריך הקודם למדנו כיצד להשתמש בt-test כדי לבחון האם יש הבדל בין ממוצעי שתי קבוצות. כדי להשוות את הממוצעים בין שלוש קבוצות או יותר נשתמש ב-ANOVA.

One-way ANOVA

One-way ANOVA עונה על השאלה האם יש הבדל בממוצעים של קטגוריה אחת מסוימת בין 3 קבוצות או יותר. השערת האפס היא שאין הבדל בממוצעים. ההשערה החלופית היא שקיים הבדל.

הדוגמה במדריך מבוססת על מסד נתונים הכולל את נתוני מידות הגוף של שלושה זני פינגווינים. נתרכז במשקל הגוף ונשאל את השאלה האם המינים נבדלים במשקלם.

במדריך זה נשתמש בפייתון כדי לעשות One-way ANOVA.

נייבא את הספריות:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as stats

מסד הנתונים כולל מידע על משקל וממדי הגוף של 3 זני פינגווינים. נוריד אותו לסביבת העבודה:

df = sns.load_dataset('penguins')

נסקור את המידע במסד:

df.head()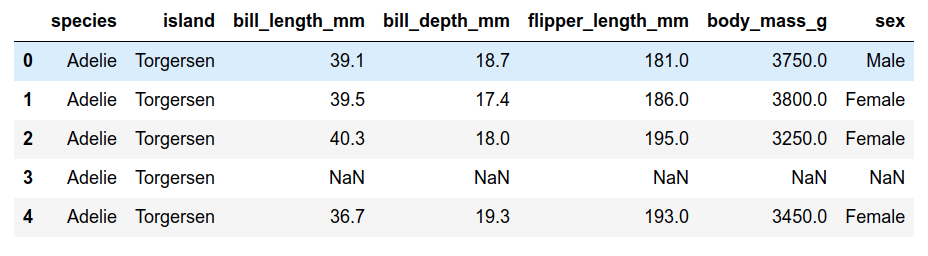

df.shape

(344, 7)

df.isnull().sum()

19

• 344 רשומות בסך הכול, בחלקם חסרים נתונים.

נסיר את הרשומות החסרות:

df = df.dropna(axis=0)

התכונה שמעניינת אותנו היא משקל הגוף. הגרף הבא מתאר את פיזור משקל הגוף של הזנים:

sns.catplot(data=df, x='species', y='body_mass_g');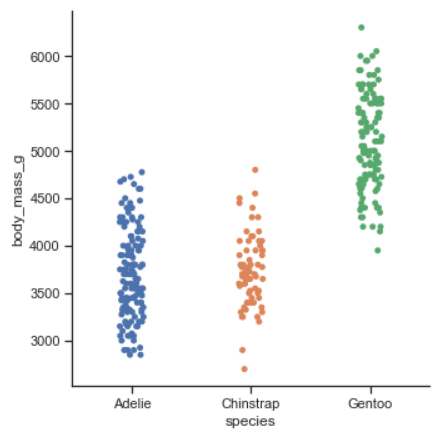

נסתכל על הנתונים גם באמצעות דיאגרמת עמודות:

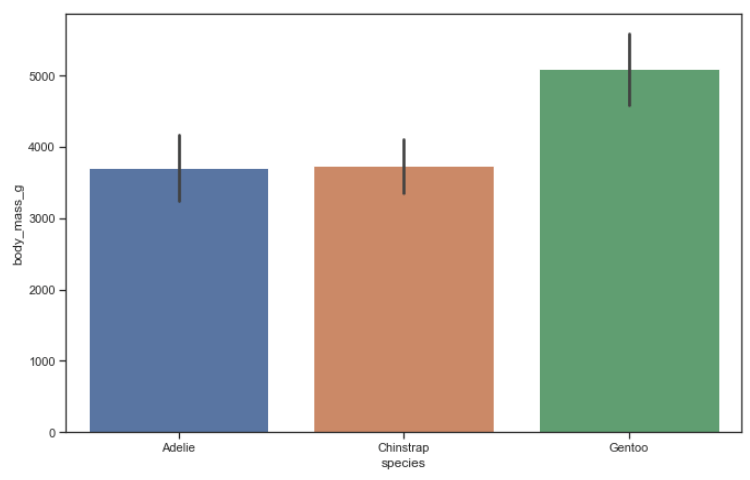
קווי השגיאה מתארים את סטיית התקן סביב הממוצע ונראה שהמין Gentoo כבד באופן משמעותי יותר בגלל שסטיית התקן שלו אינה חופפת לשניים האחרים.

האם ההבדל משמעותי מבחינה סטטיסטית?

כדי לקבל תשובה סטטיסטית לשאלה האם הממוצע של משקל הגוף שונה בין זני הפינגווינים נשתמש במבחן One-way ANOVA עם ערך קריטי (alpha) 0.05

ראשית, נפריד את את המשקלים לשלוש קבוצות:

a = df.loc[df.species=='Adelie', 'body_mass_g']
c = df.loc[df.species=='Chinstrap', 'body_mass_g']
g = df.loc[df.species=='Gentoo', 'body_mass_g']

נעשה מבחן ANOVA:

stats.f_oneway(a, c, g)

F_onewayResult(statistic=341.9, pvalue=3.74e-81)

• ה p value נמוך הרבה יותר מ-0.05 ומעיד על הבדל סטטיסטי במשקל הזנים.

אילו קבוצות גורמות להבדל?

כדי לברר אילו זנים נבדלים משמעותית נשתמש במבחנים פוסט-הוק post hoc.

גישה אחת היא לבצע t-test בין כל אחד מצמדי הזנים:

# conduct a t-test on each pair
print('a,c: ', stats.ttest_ind(a,c))
print('a,g: ', stats.ttest_ind(a,g))
print('g,c: ', stats.ttest_ind(g,c))

a,c:  Ttest_indResult(statistic=-0.42, pvalue=0.67)
a,g:  Ttest_indResult(statistic=-23.4, pvalue=1.9e-66)
g,c:  Ttest_indResult(statistic=19.3, pvalue=2.8e-46)

• קיים הבדל משמעותי בין הזן Gentoo לשני הזנים האחרים.

הבעיה עם עריכת מספר מבחנים סטטיסטיים היא שככל שנפעיל יותר מבחנים כך גדל הסיכוי לקבל תשובה שגויה. כדי להתמודד עם הבעיה אנחנו יכולים להפחית את ערך הסף (alpha) לדחיית השערת האפס. תיקון בונפרוני Bonferroni מציע לחלק את ערך הסף במספר המבחנים. במקרה זה, ערך הסף הוא 0.05 ומכיוון שערכנו 3 מבחנים, נתקן את ערך הסף ל-

alpha = 0.05/3 = 0.0167

תיקון בונפרוני הוא מאוד מחמיר. אם נקבל תוצאה משמעותית לאחר שערכנו את התיקון אנחנו יכולים בטוחים ביותר שלא דחינו את השערת האפס בטעות. בדיוק מסיבה זו אנחנו מסתכנים בקבלת השערת האפס (שאין הבדל) למרות שקיים הבדל בין הקבוצות.

מבחן פוסט הוק מחמיר פחות הוא Tukey. נדגים אותו:

from statsmodels.stats.multicomp import pairwise_tukeyhsd
tukey = pairwise_tukeyhsd(endog=df.body_mass_g,
                                            groups=df.species,  
                                             alpha=0.05) 

• הפרמטר endog הוא התכונה הנמדדת (משקל הגוף)
• הפרמטר groups הם הקטגוריות שאנו משווים (זנים של פינגווינים)
• הפרמטר alpha הוא ערך הסף לדחיית השערת האפס

נתאר את התוצאות באמצעות תרשים:

tukey.plot_simultaneous()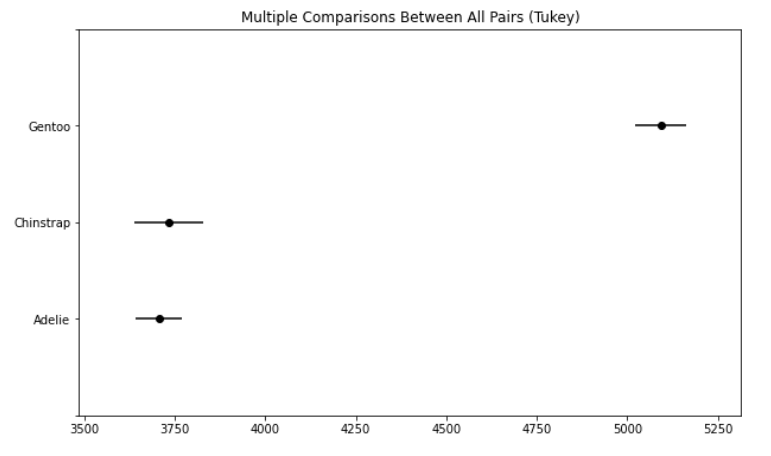

• מרווח השגיאה של המין Gentoo גבוה מהשניים האחרים. קיימת חפיפה בין המינים Chinstrap ו-Adellie. לפיכך, המין Gentoo כבד משמעותית יותר.

נסכם את תוצאות מבחן Tukey בטבלה:

tukey.summary()

• מבחן Tukey מאפשר לנו לדחות את השערת האפס שממוצע המשקל שווה בין המין Gentoo ושני המינים האחרים על פי רמת משמעותיות מתואמת 0.001 הנמוכה משמעותית יותר מערך הסף alpha = 0.05. בנוסף, המינים Adelie ו-Chinstrap הם בעלי אותו משקל ממוצע.

סיכום 

במדריך למדנו שכדי לבדוק האם קיימים הבדלים בממוצע של שלוש קבוצות או יותר לא כדאי להשתמש במבחן t-test אלא ב-ANOVA ממנו ניתן להסיק אודות קיום הבדל בין הקבוצות. מה-ANOVA לא ניתן להסיק לגבי אילו קבוצות הם השונות. כדי למצוא את הקבוצות השונות צריך לערוך מבחני פוסט הוק, דוגמת Tukey.

לכל המדריכים בנושא של למידת מכונה

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים