מבחן t-test לבחינת השערות
במדריך הקודם הסברנו מהי בדיקת A/B אבל לא הסברנו כיצד לבחון האם התוצאות הם משמעותיות. במדריך זה נכיר את הדרך המקובלת ביותר המסתמכת על בחינת השערות hypothesis testing באמצעים סטטיסטיים.
בחינת השערות היא דרך לבחון האם תוצאות של סקר או ניסוי הם בעלות משמעות סטטיסטית.
כדי לבחון את ההשערה בניסוי אנחנו מתחילים מהשערת אפס לפיה אין דבר מיוחד בתוצאות כאשר ההשערה חלופית היא שיש משהו מיוחד בתוצאות. מטרת המבחן היא לאשש את השערת האפס או לחלופין לדחות אותה ובכך לקבל את ההשערה החלופית.
לדוגמה, ניסוי הבוחן הם שינוי צבע הקישורים באתר אינטרנט מכחול לאדום משנה את יחס ההקלקות (היחס בין מספר מספר המשתמשים הנחשפים לקישור לבין כמות המקליקים עליו). השערת האפס היא שאין שינוי והיחס ישאר זהה. ההשערה החלופית היא שיהיה שינוי.
אחרי שהגדרנו את השערת האפס וההשערה החלופית, עלינו לבחור רמת משמעות (alpha) שהיא ההסתברות לכך שאת התוצאות קיבלנו במקרה. בהתאם, alpha מהווה את הסף לדחיית השערת האפס. מקובל לבחור בערך alpha של 5%. אבל במקרים רבים רצוי לבחור בערך נמוך יותר כדי להקטין את הסיכוי לזיהוי שגוי, כאשר ההבדל אינו קיים אולם ההבדל נראה משמעותי בניסוי בגלל השפעתם של גורמים אקראיים.
לאחר סיום הניסוי נחשב בשיטות שאותם נסקור במדריך את התוצאות ונקבל ערך p-value, ההסתברות לקבל את תוצאות הניסוי או קיצוניות מהם במקרה. במידה וערך p-value הוא נמוך מ-alpha נדחה את השערת האפס ונקבל את ההשערה החלופית.
ישנם מגוון של מבחנים סטטיסטיים ובמדריך זה נלמד אודות השניים הרלוונטיים ביותר לבדיקת A/B: z-test ו t-test באמצעות 4 דוגמות מקרה.
מקרה ראשון - מבחן לפרופורציות
אתר מסחר ברשת מנסה לבדוק האם שינוי של צבע כפתור הקנייה מכחול לאדום משנה את יחס ההמרה. מספר הרוכשים מתוך כמות הנכנסים לדף מתואר באמצעות:
N(users bought)/N(total users)
כדי להגיע למסקנה אנחנו קודם כל צריכים להגדיר מהם ההשערות אותם אנו בוחנים.
השערת האפס היא ששינוי צבע הכפתור אינו משנה את יחס ההמרה. ההשערה החלופית היא שקיים שינוי ביחס ההמרה. רמת הסף אשר תכריע בין החלופות היא alpha של 0.05
לצורך הניסוי, נערכה דגימה של 2000 כניסות לדף של מוצר מסוים. במחצית אקראית של 1000 כניסות נחשפו המשתמשים לכפתור הכחול המקורי. המחצית האחרת של המשתמשים ראו כפתור אדום שאת השפעתו מעוניינים לבחון.
יחס ההמרה בקבוצת הביקורת, שראתה כפתור כחול, היה 1.2% ובקבוצת הניסוי 2.5%. בהתאם לכך, ש- 12 מתוך 1000 משתמשים הקליקו בקבוצת הביקורת ו-25 מתוך 1000 בקבוצת הניסוי.
זו דוגמה למבחן המשווה בין פרופורציות עבור שתי קבוצות.
האם אפשר להסיק מהתוצאות ששינוי צבע הכפתור גרם לשינוי ביחס ההמרה? או אולי התוצאות הם מקריות?
ישנם מגוון מבחנים סטטיסטיים אבל כיוון שאנו עוסקים בהתפלגות בינומית כאשר ישנם שתי חלופות אפשריות בלבד, משתמש הקליק או לא הקליק, אמת או שקר, 1 או 0, נשתמש ב-z-test כדי להכריע האם ממוצעי שתי האוכלוסיות שונות משמעותית.
את המבחן בפועל נעשה באמצעות הפונקציה proportions_ztest מספריית statsmodels:
count = np.array([12, 25])
nobs = np.array([1000, 1000])
stats, pval = proportions_ztest(count, nobs, alternative="two-sided")
print(pval)- Count - הם מספר ההקלקות
- Nobs - הוא גודל האוכלוסיה
- Alternative - הוא כיוון ההשפעה החלופית. אם היינו סבורים ששינוי צבע הכפתור יעלה היינו משתמשים בערך 'larger'. לחלופין, האפשרות 'smaller' משמשת אם אנו סבורים שההשפעה תגרום להפחתה. ברירת המחדל היא 'two-sided' אם איננו יודעים לנחש מראש את כיוון השינוי.
ערך p-value שהתקבל כתוצאה מבחינת ההשערות הוא 0.031 ופירושו שיש סיכוי של 3.1% ששתי הקבוצות הם מאותה אוכלוסייה אבל כיוון שערך הסף alpha שבחרנו עבור הניסוי הוא 5%, ערך גדול יותר מp-value, נדחה את השערת האפס ונסיק ששינוי צבע הכפתור גרם לשינוי ביחס ההמרה.
אם היינו בוחרים ערך סף alpha של 1%, הנמוך מערך p-value שהתקבל בניסוי היינו דוחים את ההשערה החלופית ומסיקים ששינוי הצבע לא גרם לשינוי.
מקרה שני - האם קבוצת הניסוי שונה מהאוכלוסייה הכללית
אתר סחר אלקטרוני מעוניין לבדוק האם משתמשים שיקבלו מתנה יוציאו יותר כסף בפלטפורמה. צוות האתר דגם 30 משתמשים אקראיים ונתן להם מתנה, ואז סיכם את גובה הרכישות בחודש שלאחר מתן המתנה.
after = [8,11,13,20,11,21,9,13,12,11,0, 20,30,21,10,0, 21,31,22,12,0, 20,31,18,10,0, 20,30,24,14]במקביל, משתמשי האתר שלא קיבלו מתנות הוציאו בממוצע 11.5$ באותו החודש.
נחשב את ממוצע אוכלוסיית הניסוי:
np.mean(after) # 15.433שאלת הניסוי היא האם העובדה שמשתמשים קיבלו מתנות גרמה להם לקנות ביותר כסף באתר. בהתאם השערת האפס היא שאין שינוי או שההוצאה הממוצעת פחתה. ההשערה החלופית היא שהמשתמשים שקיבלו כסף הוציאו יותר.
מערך ניסוי זה מדגים מצב בו השאלה הנבחנת היא האם קבוצת הניסוי שונה מהאוכלוסייה הכללית ממנה היא נלקחה.
כיוון שההתפלגות אינה בינומית נשתמש במבחן t-test הבוחן האם ממוצע האוכלוסיות שונה סטטיסטית. יש כמה אפשרויות של t-test. במקרה זה אנחנו רוצים לבחון האם קיים הבדל בממוצע בין אוכלוסיית הניסוי לאוכלוסייה הכללית ממנה היא נדגמה ועל כן נשתמש במבחן one-sample t-test עם ערך סף alpha של 0.05
את המבחן נערוך באמצעות הפונקציה ttest_1samp של ספריית scipy:
scipy.stats.ttest_1samp(a = after, popmean = 11.5, alternative='greater')- a - מערך המכיל את התוצאות של אוכלוסיית הניסוי
- popmean - הוא ממוצע האוכלוסייה הכללית
- הפרמטר alternative יקבל את הערך greater כדי לבחון האם מקבלי המתנה רכשו יותר
התוצאה:
Ttest_1sampResult(statistic=2.361612962428935, pvalue=0.025125960217142165)
p-value של 2.5% , משמע שיש סיכוי של 2.5% בלבד שההבדל הוא אקראי. מכיוון שערך p-value נמוך יותר מערך הסף alpha נוכל לדחות את השערת האפס ולהסיק שהמשתמשים שקיבלו מתנה רוכשים ביותר כסף.
מקרה שלישי - השוואה בין שתי אוכלוסיות בלתי תלויות
אתר הסחר האלקטרוני רצה לבחון האם קבלת מתנה או הנחה בקנייה יגרמו לשינוי בהוצאה הכספית של משתמשים באתר.
בהתאם, הניסוי צריך לכלול שתי קבוצות: אחת שמקבלת הנחות ושנייה שמקבלת מתנות.
זו דוגמה להשוואה בין שתי אוכלוסיות בלתי תלויות.
השערת האפס היא שלא ימצא הבדל בהוצאה הכספית בין הקבוצה שמקבלת הנחה לאילו שמקבלים מתנות. כאשר מראש נקבעה רמת סף, alpha, של 5%.
תוצאות הניסוי:
discount = [10,0, 11,30,22,12,0,11,13,20,10,0, 10,32,21,11,10,11,32,22,10,0, 15,30,20,10,10,15,30,20]
perks = [8 ,11,13,20,11,21,9,13,12,11,0, 20,30,21,10,0, 21,31,22,12,0, 20,31,18,10,0, 20,30,24,14]הממוצעים המחושבים:
np.mean(discount) # 14.93
np.mean(perks) # 15.43מלמדים על הוצאה כספית מעט גבוהה יותר בקרב מקבלי המתנות (perks) מאשר בין מקבלי ההנחות (discount).
אבל האם השוני הוא משמעותי? לפני שנבחן את ההשערה הזו ננסה לקבל תחושה לגבי הנתונים.
נעזר ב-pandas לבחינת מדדי מרכז ופיזור של הדוגמאות:
print("discount")
pd.DataFrame(discount).describe()| count | 30.000000 |
|---|---|
| mean | 14.933333 |
| std | 9.493858 |
| min | 0.000000 |
| 25% | 10.000000 |
| 50% | 11.500000 |
| 75% | 20.750000 |
| max | 32.000000 |
print("perks")
pd.DataFrame(perks).describe()| count | 30.000000 |
|---|---|
| mean | 15.433333 |
| std | 9.122474 |
| min | 0.000000 |
| 25% | 10.250000 |
| 50% | 13.500000 |
| 75% | 21.000000 |
| max | 31.000000 |
טוב מראה עיניים מתיאור באמצעות טבלאות מספרים. נעזר ב- matplotlib לצורך הצגת box-plot:
data_to_plot = [discount, perks]
fig, ax = plt.subplots(1, 1, sharex=True, sharey=True)
bp = ax.boxplot(data_to_plot)
ax.set_xticklabels(["discount", "perks"])
plt.ylabel("Total $");
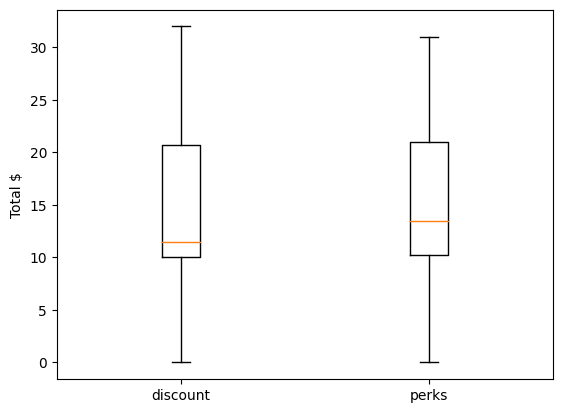
כדי לבחון את ההשערה באופן מוצק יותר נפעיל מבחן סטטיסטי מסוג t-test עבור שתי אוכלוסיות בלתי תלויות.
לצורך עריכת two sample t-test נשתמש בפונקציה ttest_ind של scipy:
scipy.stats.ttest_ind(a = discount, b = perks, equal_var=False)- a - מערך המכיל את התוצאות של אוכלוסייה אחת
- b - מערך המכיל את התוצאות של אוכלוסייה שנייה שאינה תלויה בראשונה
- לפרמטר equal_var נתתי את הערך False כי ה-variance שונה בין האוכלוסיות
התוצאה:
Ttest_indResult(statistic=-0.20800084972903837, pvalue=0.8359581297638717)ערך p-value של 84% מלמד שהאוכלוסיות אינם נבדלות מבחינה סטטיסטית עבור הפרמטר הנבדק בניסוי.
מקרה רביעי - השוואת אותה אוכלוסייה בנקודות זמן שונות
במקרה השלישי הדגמנו שימוש בהסקה סטטיסטית למציאת ההבדל בין שתי קבוצות בלתי תלויות אבל ייתכנו מצבים של תלות כאשר נרצה לחזור ולמדוד את אותו מדגם, לדוגמה בנקודות זמן שונות.
אתר הסחר האלקטרוני רצה לבדוק את השפעת הקשחה במדיניות ההחזרה של מוצרים על כמות הכסף שמוציאים המשתמשים. לפני שהוא הכיל את שינוי המדיניות באופן גורף על כלל המשתמשים, צוות האתר החליט לנקוט משנה זהירות ולבחון את ההשפעה על קבוצה של 30 משתמשים שיבחרו באקראי, ורק עליהם יכילו את המדיניות החדשה. השערת האפס של הניסוי היא שהקשחת המדיניות לא תגרום לירידה בהוצאות. ההשערה החלופית היא שתהיה ירידה. שיעור הסף שמתחת לו דוחים את השערת האפס הוא 5%.
הרכישות של 30 המשתתפים בניסוי במהלך החודש שקדם לשינוי מסוכמים במערך before:
before = [20,0, 11,30,22,12,0,11,130,20,100,0, 110,32,21,11,10,11,32,220,10,45, 85,30,20,10,10,15,30,200]הרכישות של אותה אוכלוסיה לאחר שינוי המדיניות מסוכמים במערך after:
after = [8 ,11,13,20,11,21,9,13,12,0,0, 20,30,21,10,0, 21,31,22,12,0, 20,31,18,10,0, 20,30,34,24]כיוון שאנחנו מעוניינים לבחון את שינוי ממוצע הרכישה בתוך אותה אוכלוסיית מדגם עקב השינוי נשתמש במבחן paired t-test אותו נערוך באמצעות הפונקציה ttest_rel:
scipy.stats.ttest_rel(a=after, b=before, alternative='less')התוצאות:
Ttest_relResult(statistic=-2.5654832773313028, pvalue=0.007869029981879192)
p-Value של 0.8% מלמדות שהסיכוי שהירידה ברכישות היא מקרית הוא נמוך מערך הסף של 5%, ולכן נקבל את ההשערה החלופית שהקשחת מדיניות ההחזרה תגרום לירידה ברכישות.
לסיכום
| מקרה | מבחן | פונקציה של פייתון |
|---|---|---|
| השוואת פרופורציות כאשר התוצאה בינארית ומספר התוצאות מכל סוג גבוה מ-20 | z-test | statsmodel.proportions.ztest |
| האם המדגם שונה מהאוכלוסייה הכללית | one-sample t-test | scipy.stats.ttest_1samp |
| שני מדגמים בלתי תלויים | two-sample t-test | scipy.stats.ttest_ind |
| אותה קבוצה לפני ואחרי | paired t-test | scipy.stats.ttest_rel |
לכל המדריכים בנושא של למידת מכונה
אהבתם? לא אהבתם? דרגו!
0 הצבעות, ממוצע 0 מתוך 5 כוכבים



המדריכים באתר עוסקים בנושאי תכנות ופיתוח אישי. הקוד שמוצג משמש להדגמה ולצרכי לימוד. התוכן והקוד המוצגים באתר נבדקו בקפידה ונמצאו תקינים. אבל ייתכן ששימוש במערכות שונות, דוגמת דפדפן או מערכת הפעלה שונה ולאור השינויים הטכנולוגיים התכופים בעולם שבו אנו חיים יגרום לתוצאות שונות מהמצופה. בכל מקרה, אין בעל האתר נושא באחריות לכל שיבוש או שימוש לא אחראי בתכנים הלימודיים באתר.
למרות האמור לעיל, ומתוך רצון טוב, אם נתקלת בקשיים ביישום הקוד באתר מפאת מה שנראה לך כשגיאה או כחוסר עקביות נא להשאיר תגובה עם פירוט הבעיה באזור התגובות בתחתית המדריכים. זה יכול לעזור למשתמשים אחרים שנתקלו באותה בעיה ואם אני רואה שהבעיה עקרונית אני עשוי לערוך התאמה במדריך או להסיר אותו כדי להימנע מהטעיית הציבור.
שימו לב! הסקריפטים במדריכים מיועדים למטרות לימוד בלבד. כשאתם עובדים על הפרויקטים שלכם אתם צריכים להשתמש בספריות וסביבות פיתוח מוכחות, מהירות ובטוחות.
המשתמש באתר צריך להיות מודע לכך שאם וכאשר הוא מפתח קוד בשביל פרויקט הוא חייב לשים לב ולהשתמש בסביבת הפיתוח המתאימה ביותר, הבטוחה ביותר, היעילה ביותר וכמובן שהוא צריך לבדוק את הקוד בהיבטים של יעילות ואבטחה. מי אמר שלהיות מפתח זו עבודה קלה ?
השימוש שלך באתר מהווה ראייה להסכמתך עם הכללים והתקנות שנוסחו בהסכם תנאי השימוש.