מבחני חי בריבוע לבדיקת השערות עם פייתון

משתמשים במבחני חי בריבוע Chi-Square לבחינת השערות על התפלגות האוכלוסייה לקטגוריות.

מבחן חי בריבוע בוחן את שכיחות התצפיות בקטגוריות, ומנסה למצוא האם קטגוריה אחת (או שילוב של קטגוריות) הוא נפוץ יותר מהצפוי.

קיימים שלושה סוגים של מבחני חי בריבוע:

• מבחן טיב התאמה
• מבחן לאי תלות
• מבחן להומוגניות

מבחן לטיב התאמה goodness of fit

מבחן לטיב התאמה בוחן האם התפלגות של משתנה 1 תואם להתפלגות צפויה.

דוגמאות:

• האם שכיחות התוצאות בהטלת מטבע שונה מהצפוי (1:1)?
• האם שיעור התפוחים הפסולים ליצוא שווה בין 3 שיטות טיפול שונות?

את הנתונים למבחני חי בריבוע נסדר בטבלת שכיחויות.

לדוגמה, טבלת שכיחויות של הטלת מטבע 100 פעמים:

האם העובדה ששכיחות התוצאות שונה מ-50:50 מעידה על כך שהמטבע מוטה? או שהתוצאה אינה מובהקת מספיק? על זה יענה מבחן לטיב התאמה.

לדוגמה, חברת "יוסף ובנותיו" עורכת סקר שנתי כדי לבחון את מידת שביעות הרצון של לקוחותיה משירותי החברה. שביעות הרצון מתחלקת ל-3 קטגוריות: "מאוד מרוצה", "ככה ככה", "לא מרוצה". הנהלת החברה מעריכה ש-30% ישיבו שהם "מאוד מרוצים", 60% ישיבו שהם "ככה ככה" ו-10% לא יהיו מרוצים.

לאחר עריכת הסקר על 1000 לקוחות, הסתבר ש-350 השיבו שהם "מאוד מרוצים", 500 השיבו שהם "ככה ככה" ו-150 השיבו שאינם מרוצים.

חברת "יוסף ובנותיו" מעוניינת לגלות האם תוצאות הסקר שונות משמעותית מההשערה הראשונית שלהם. כדי לענות על השאלה הם יכולים להשתמש במבחן חי בריבוע מסוג טיב התאמה אשר בודק האם תוצאות סקר/מחקר תואמות התפלגות צפויה.

השערת האפס (H0) : התפלגות (=הפרופורציה) של התשובות במדגם זהה לציפיות.

ההשערה החלופית (H1) : התפלגות התוצאות שונה מהמשוער.

אם השערת האפס Ho היא נכונה אז הצפי הוא להתפלגות הבאה בתשובות לסקר:

• התנאי לעריכת מבחן חי בריבוע הוא שהשכיחות בכל תא לא תפחת מ-5.

כדי לבחון את ההשערה האם התוצאות בפועל שונות משמעותית מהצפי נפחית מכל אחת מהתוצאות בפועל שהתקבלו בסקר את התוצאות הצפויות:

$$ OBS_1 - EXP_1 $$

נעשה את אותו הדבר עבור כל אחת מהקטגוריות (שאלות הסקר, במקרה שלנו), ונחבר את ההפרשים:

$$ (OBS_1 - EXP_1) + … + (OBS_3 - EXP_3) = 0 $$

• התוצאה בהכרח תהיה 0.

כדי למנוע את איפוס התוצאה נעלה כל אחד מההפרשים בריבוע:

$$ (OBS_1 - EXP_1)^2 + … + (OBS_3 - EXP_3)^2 $$

בנוסף, אנחנו צריכים לנרמל כי הפרש של נקודה 1 מתוך 5 הוא משמעותי אבל הפרש של 1 מתוך 100 הוא קטן ואף זניח. הדרך לנרמל היא על ידי חלוקה בערכים הצפויים:

$$ \frac{(OBS_1 - EXP_1)^2}{EXP_1} + … + \frac{(OBS_3 - EXP_3)^2}{EXP_3} $$

ננסח בהתאם את הנוסחה לחישוב האומד (סטטיסט) עבור מבחן לבחינת השערות חי בריבוע :

$$ \chi^2 = \sum_{n=1}^{N} \frac{(OBS_n - EXP_n)^2}{EXP_n} $$

נציב את הנתונים שלנו בנוסחה כדי לחשב את האומד של חי בריבוע עבור הסקר:

$$ \chi^2 = \frac{(115 - 100)^2}{100} + \frac{(565 - 600)^2}{600} + \frac{(320 - 300)^2}{300} = 5.625 $$

• האומד הינו 5.625, בו נשתמש כדי להעריך עד כמה המידע שלנו תואם את התפלגות של חי בריבוע עבור שאלת המחקר.

ההתפלגות של חי בריבוע משנה את צורתה בהתאם לדרגות החופש. נעזר בפייתון כדי להציג את צורת ההתפלגות עבור דרגות חופש שונות:

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chi2

# Degrees of freedom
dfs = [1, 2, 3, 4, 6, 10]

# Range of values for the chi-square distribution
x = np.linspace(0, 30, 1000)

# Plot the chi-square distribution for each degree of freedom
for df in dfs:
    plt.plot(x, chi2.pdf(x, df), label=f'df={df}')

plt.title('Chi-Square Distribution')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.ylim(0, 0.5)  # Limit y-axis to 0.5
plt.show()

התפלגות חי בריבוע עבור דרגות חופש שונות:

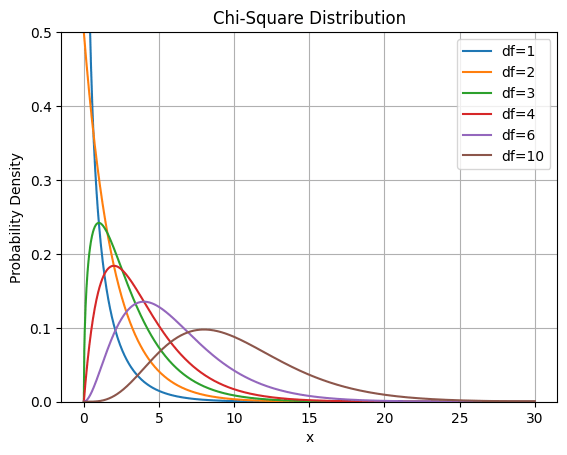
במקרה שלנו יש 3 קטגוריות (של שאלות) מה שאומר 3 פיסות מידע עצמאיות אז לפי הנוסחה לחישוב דרגות חופש צריך להפחית 1 מכמות פיסות המידע כדי לחשב את דרגות החופש:

$$ DF = count(data) - 1 $$

• הסיבה היא שדרגות החופש משתנות לפי כמות המשתנים העצמאיים, ואם ידועים לנו הערכים של 2 מתוך 3 קטגוריות ואת הסה"כ אז ניתן לחשב את הערך עבור הקטגוריה השלישית כך שהיא אינה עצמאית. לכן, הנוסחה לחישוב דרגות חופש מפחיתה 1 ממספר פיסות המידע.

ההסתברות של הסטטיסטיקה שחישבנו של חי בריבוע (אומד) היא 5.625. האם היא משמעותית?

כדי להגיע למסקנה האם התוצאה משמעותית, אנחנו צריכים להשוות את האומד לערך הקריטי עבור רמת המובהקות הרצויה:

• אם הערך הקריטי גבוה יותר מהאומד, אז התוצאה משמעותית סטטיסטית.
• אם הערך הקריטי נמוך יותר מהאומד, אז התוצאה אינה משמעותית סטטיסטית.

נעזר בפייתון לחישוב הערך הקריטי עבור 2 דרגות חופש ורמת מובהקות 0.05:

import scipy.stats as stats


# Degrees of freedom
df = 2


# Significance level
alpha = 0.05


# Find the critical value
critical_value = stats.chi2.ppf(1 - alpha, df)


print(f"Critical value for chi-square with {df} degrees of freedom at alpha = 0.05: {critical_value:.3f}")

התוצאה:

Critical value for chi-square with 2 degrees of freedom at alpha = 0.05: 5.991

• מכיוון שהאומד שלנו 5.625 הוא נמוך יותר מהערך הקריטי (עבור רמת מובהקות alpha=0.05) שערכו 5.991 אנחנו לא יכולים לדחות את השערת האפס, ולפיכך נסיק שהתוצאות בפועל אינם שונות מהצפי.

נעזר בפייתון כדי להציג גרף שמשווה בין הערך הקריטי והמחושב עבור מבחן חי בריבוע עם 2 דרגות חופש:

import numpy as np
import scipy.stats as stats
from scipy.stats import chi2
import matplotlib.pyplot as plt


chi_square_stat = chi_square_stat


# Degrees of freedom
df = 2


# Significance level
alpha = 0.05


# Find the critical value
critical_value = stats.chi2.ppf(1 - alpha, df)


# Generate x values
x = np.linspace(0, 20, 1000)


# Plot the chi-square PDF
plt.figure(figsize=(8, 6))
plt.plot(x, chi2.pdf(x, df), color='#5fad0d', label=f'Chi-square with {df} DF')


# Add vertical lines for p-value and critical value
plt.axvline(x=chi_square_stat, color='#504e4f', linestyle='--', label=f'Chi square statisic = {chi_square_stat}')
plt.axvline(x=critical_value, color='r', linestyle='--', label=f'Critical value = {critical_value:.3f}')


# Shade the region beyond the p-value
plt.fill_between(x, chi2.pdf(x, df), where=(x > chi_square_stat), color='#d5dee9', alpha=0.5)


# Add labels and legend
plt.xlabel('Chi-square Value')
plt.ylabel('Probability Density')
plt.title('Comparison of Chi-Square Statistic and Critical Value (alpha=0.05)')
plt.legend()


# Show plot
plt.grid(True)
plt.show()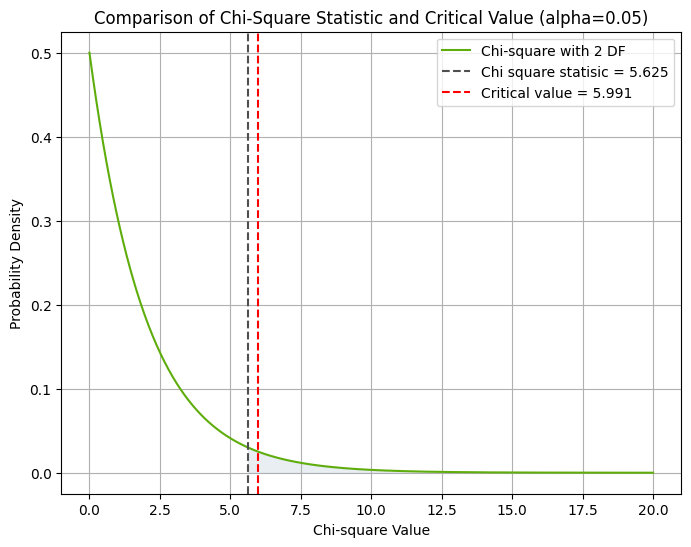

דרך משלימה להעריך האם התוצאות משמעותיות סטטיסטית היא באמצעות חישוב p value והשוואתו לרמת מובהקת רצויה (בד"כ, 0.05) .

• רמת מובהקות (α): סף סטטיסטי המשמש להחלטה אם לדחות את השערת האפס.
• ערך p-value: ההסתברות לקבל תוצאות קיצוניות (או קיצוניות יותר) כמו התוצאות שנצפו, בהנחה שהשערת האפס נכונה.

נחשב את ה p value עבור 2 דרגות חופש ורמת מובהקות 0.05:

# Calculate p-value for 2 degrees of freedom
chi_square_stat = chi_square_stat


p_value = 1 - stats.chi2.cdf(x = chi_square_stat, df = 2)


print(f"p_value = {p_value:.3f}")

התוצאה:

p_value = 0.060

נשווה את ה p-value המחושב לרמת המובהקות 0.05 כדי להסיק אם התוצאה משמעותית סטטיסטית:

# Interpretation
if p_value > 0.05:
    print("The results of the experiment are not statistically significant.")
else:
    print("The results of the experiment are statistically significant.")

התוצאה:

The results of the experiment are not statistically significant.

בגלל ש p-value המחושב עבור התוצאות שלנו ערכו הוא 0.06 ערך גבוה מ-0.05 (רמת המובהקות שקבענו מראש לניסוי) נסיק שתוצאות הניסוי אינם שונות משמעותית מהצפי.

מבחן חי בריבוע לטיב התאמה בדרך הקלה עם פונקציה של פייתון

עד עכשיו ראינו את הדרך הארוכה יותר כי חשוב להבין איך המבחן לטיב התאמה עובד. אבל בפייתון יש אפשרות לערוך מבחן השערות חי בריבוע לטיב התאמה בדרך קצרה בהרבה.

נערוך מבחן חי בריבוע לטיב התאמה בדרך הקצרה באמצעות הפונקציה stats.chisquare() של ספריית scipy שהפרמטרים היחידים שהיא צריכה לקבל הם מערך התוצאות בפועל (obs) ומערך התוצאות הצפויות (exp):

import numpy as np
import scipy.stats as stats


# Observed and expected data
obs = np.array([320, 565, 115])
exp = np.array([300, 600, 100])


# Perform chi-square test
chi2_stat, p_value = stats.chisquare(obs, exp)


print(f"Chi-square statistic = {chi2_stat:.3f}")


print(f"p_value = {p_value:.3f}")

התוצאה:

Chi-square statistic = 5.625

p_value = 0.060

• התוצאה מלמדת שתוצאות הסקר אינם חורגות מהצפי (השערת האפס) עבור רמת מובהקות alpha=0.05

נסכם, מבחן חי בריבוע לטיב התאמה (goodness-of-fit) בוחן עד כמה הפרופורציה הצפויה מתאימה לתוצאות המחקר. דרך אחת לזהות האם מבחן ההשערות אותו יש לערוך הוא לטיב התאמה היא אם הנתונים שלנו מופיעים בשורה אחת וכוללים כמה קטגוריות מה שאומר שאנחנו מתעניינים במשתנה יחיד.

מבחן חי בריבוע לאי תלות

מבחן חי-בריבוע לאי-תלות Chi-square test of independence בודק האם קיים קשר בין שני משתנים קטגוריים באותה אוכלוסייה. במילים אחרות, הוא בודק האם שני המשתנים תלויים אחד בשני. בניגוד למבחן לטיב התאמה, מבחן זה לא משווה משתנה יחיד לאוכלוסייה תיאורטית, אלא בודק את הקשר בין שני משתנים מתוך אותה אוכלוסייה.

לדוגמה, מחקר בדק אם ישנו קשר בין טעם קולינרי לסוג סרט העלה את התוצאות הבאות בקרב 300 משתתפים:

שתי הקטגוריות בטבלת השכיחויות הם "טעם קולינרי" ו"ז'אנר קולנועי".

1. טעם קולינרי: "איטלקי", "תאילנדי", "ג'אנק פוד"
2. ז'אנר קולנועי: "קומדיה", "פעולה", "אנימציה"

נשתמש במבחן חי בריבוע לאי תלות (Chi-square test of independence) כדי לקבוע האם משתנה קטגורי אחד (ז'אנר קולנועי) משפיע על קטגוריה שנייה (טעם קולינרי).

השערת האפס (H0): אין קשר בין טעם קולינרי לסוג סרט.

ההשערה החלופית (H1): קיים קשר בין טעם קולינרי לסוג סרט.

בשביל לחשב את הערכים הצפויים בכל תא בטבלה תחת ההנחה שהשערת האפס נכונה (ואין תלות בין הקטגוריות) נחשב את הסך הכל עבור כל שורה ועמודה, ואז נכפול את הסה"כ של השורה בסה"כ של העמודה ונחלק בסה"כ התצפיות.

בדוגמה שלנו, נחשב את הסה"כ של השורות והעמודות ונוסיף לטבלת השכיחויות:

נחשב את הצפי עבור כל תא בנפרד על ידי הכפלת הסה"כ של השורה בסה"כ של העמודה וחלוקה בסה"כ הכללי (300). לדוגמה, כדי לחשב את הצפי עבור התא שמצליב "קומדיה" עם אוכל "איטלקי" נכפיל את הסה"כ של השורה (105) בסה"כ של העמודה (110) ונחלק בסה"כ הכללי (300).

$$ expected(comedy, italian) = 105*110/300 $$

כדי לחשב את האומד של חי בריבוע לאי תלות נשתמש באותה הנוסחה בה השתמשנו עבור חי בריבוע לטיב התאמה:

$$ \chi^2 = \sum_{n=1}^{N} \frac{(OBS_n - EXP_n)^2}{EXP_n} $$

• עבור כל תא בטבלה נפחית את הצפי מהתוצאה בפועל נעלה בריבוע ונחלק בצפי. לאחר מכן, נסכום את תוצאות החישוב של כל התאים כדי לקבל את האומד של חי בריבוע לטיב התאמה.

אפשר לחשב ידנית אבל למה להתאמץ. פייתון יערוך את החישובים למעננו ביתר קלות.

טבלת התוצאות של הסקר נתונה בקוד הבא:

import numpy as np
import pandas as pd


# Obsrved values
cols = ["Italian", "Thai", "Junk"]
index = ["Comedy", "Action", "Animation"]
comedy = [47, 38, 20]
action = [30, 30, 35]
animation = [33, 32, 35]


print("Observed values:")
observed_df = pd.DataFrame([comedy, action, animation], columns=cols, index=index)
observed_df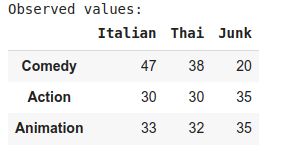

נחשב את הצפי. כמו שאמרנו, עבור כל תא בטבלה ע"פ הנוסחה:

# Calculate row and column totals
col_totals = np.array(comedy) + np.array(action) + np.array(animation)
row_totals = [sum(comedy), sum(action), sum(animation)]


# Calculate total observations
total_obs = sum(row_totals)


# Calculate expected values for each cell
expected_values = []
for i in range(len(index)):
   row_expected = []
   for j in range(len(cols)):
       expected = (row_totals[i] * col_totals[j]) / total_obs
       row_expected.append(expected)
   expected_values.append(row_expected)


# Create DataFrame for expected values
expected_df = pd.DataFrame(expected_values, columns=cols, index=index)


# Print DataFrame
print("Expected values:")
expected_df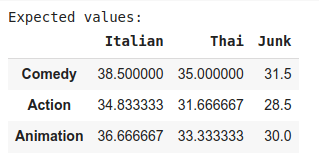

כדי לחשב את האומד של חי בריבוע נסכום את הערך של כל אחד מהתאים בטבלה:

# Convert DataFrames to NumPy arrays for efficient calculation
observed = observed_df.to_numpy()
expected = expected_df.to_numpy()


# Calculate Chi-Square statistic (sum of squared differences between observed and expected, divided by expected values)
chi_square_stat = ((observed - expected)**2 / expected).sum().sum()


# Print the calculated chi-square statistic with formatting
print(f"Chi square statistic = {chi_square_stat:.3f}")

האומד של חי בריבוע אותו חישבנו הוא:

Chi square statistic = 9.826

כדי לחשב את מספר דרגות החופש (degrees of freedom) עבור מבחן חי בריבוע לאי תלות נכפול את מספר העמודות של טבלת הנתונים פחות 1 במספר השורות פחות 1:

$$ DF = (ROWS - 1) (COLS - 1) $$

במקרה שלנו, יש לנו 3 סיווגים בכל אחת מ-2 הקטגוריות, ולכן מספר דרגות החופש הוא 4:

$$ DF = (3 - 1) (3 - 1) = 4 $$

נחשב את הערך הקריטי עבור 4 דרגות חופש ורמת מובהקות 0.05:

import scipy.stats as stats

# Degrees of freedom
df = 4

# Significance level
alpha = 0.05

# Find the critical value
critical_value = stats.chi2.ppf(1 - alpha, df)

print(f"Critical value for chi-square with {df} degrees of freedom at alpha = 0.05: {critical_value:.3f}")

Critical value for chi-square with 4 degrees of freedom at alpha = 0.05: 9.488

האומד של חי בריבוע שחישבנו 9.826 הוא גבוה יותר מהערך הקריטי 9.488 ולכן נדחה את השערת האפס שהקטגוריות אינם תלויות.

הגרף אותו יצור הקוד להלן משווה בין האומד לבין הערך הקריטי:

import numpy as np
import scipy.stats as stats
from scipy.stats import chi2
import matplotlib.pyplot as plt

df = 4

chi_square_stat = 9.826

critical_value = 9.488

# Generate x values
x = np.linspace(0, 20, 1000)

# Plot the chi-square PDF
plt.figure(figsize=(8, 6))
plt.plot(x, chi2.pdf(x, df), color='#5fad0d', label=f'Chi-square with 4 DF')

# Add vertical lines for p-value and critical value
plt.axvline(x=chi_square_stat, color='#504e4f', linestyle='--', label=f'Chi square statisic = {chi_square_stat}')
plt.axvline(x=critical_value, color='r', linestyle='--', label=f'Critical value = {critical_value:.3f}')

# Shade the region beyond the p-value
plt.fill_between(x, chi2.pdf(x, df), where=(x > chi_square_stat), color='#d5dee9', alpha=0.5)

# Add labels and legend
plt.xlabel('Chi-square Value')
plt.ylabel('Probability Density')
plt.title('Comparison of Chi-Square Statistic and Critical Value (alpha=0.05)')
plt.legend()

# Show plot
plt.grid(True)
plt.show()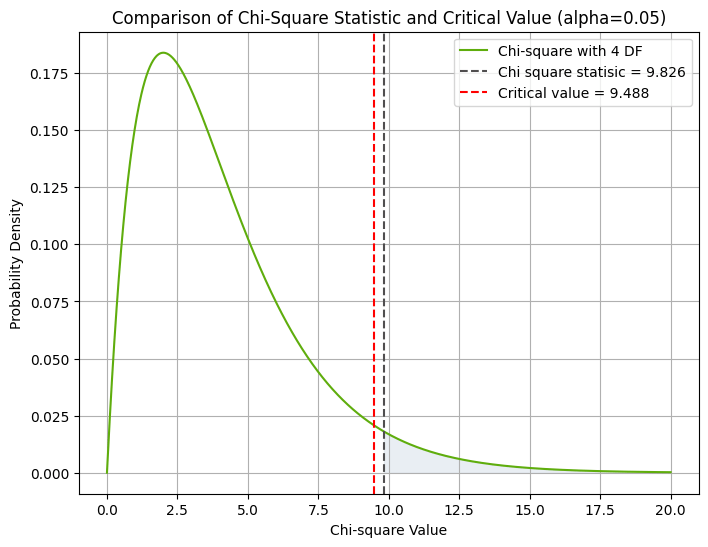

אם ערך האומד של המבחן הסטטיסטי גדול מהערך הקריטי, המשמעות היא שהנתונים הנצפים סוטים משמעותית מהנתונים הצפויים תחת השערת האפס. מה שאומר שישנן ראיות מספיקות לדחיית השערת האפס, ומעיד על קשר או תלות מובהקת סטטיסטית בין המשתנים הנבדקים במבחן השערות לאי תלות.

דרך מקבילה לבחינה האם התוצאות שונות משמעותית היא באמצעות השוואת p value לרמת מובהקות (לרוב, 0.05=α).

נחשב את ה-p value עבור 4 דרגות חופש:

# Calculate the p-value (area to the right of the Chi-Square statistic)
p_value = 1 - stats.chi2.cdf(x=chi_square_stat, df=4)

# Print the calculated p-value with formatting
print(f"P value = {p_value:.3f}")

הערך המחושב הינו:

P value = 0.043

מכיוון ש-p value של הנתונים הוא 0.043 והוא נמוך יותר מרמת מובהקות 0.05 אנחנו יכולים לדחות את השערת האפס H0 ובהתאם להסיק שקיים קשר בין טעם קולינרי והעדפות קולנועיות.

מבחן חי בריבוע לאי תלות בדרך הקלה עם פונקציה של פייתון

פייתון מאפשר לנו לעשות את מבחן חי בריבוע לאי תלות בקלות רבה על ידי העברת התוצאות שהתקבלו בפועל כפרמטר לפונקציה stats.chi2_contingency() של ספריית scipy:

import scipy.stats as stats

result = stats.chi2_contingency(observed=observed_df)
chi_square_stat = result[0]
p_value = result[1]
df = result[2]  # Degrees of freedom
expected = result[3]  # Array of expected frequencies

print("expected frequency")
print(expected)

print(f"chi square statistic = {chi_square_stat:.3f}")

print(f"p value = {p_value:.3f}")

התוצאות, כפי שניתן לראות, הם בהסכמה למה שחישבנו קודם לכן בדרך הארוכה:

expected frequency
[[38.5        35.         31.5       ]
 [34.83333333 31.66666667 28.5       ]
 [36.66666667 33.33333333 30.        ]]

chi square statistic = 9.826

p value = 0.043

לסיכום, מבחן חי בריבוע לאי תלות הוא כלי שימושי לבחינת קשר בין שני משתנים קטגוריים.

Chi-Square test for homogeneity מבחן חי בריבוע להומוגניות

המבחן להומוגניות בוחן האם דוגמאות שונות באות מאותה אוכלוסיה.

הוא יכול לבדוק, לדוגמה, האם אחוזי הקבלה שונים בין גברים לנשים לפקולטות השונות באוניברסיטה (מדעים, רפואה, הנדסה, מדעי הרוח). דרך העבודה זהה למבחן חי בריבוע לאי תלות.

לסיכום

מבחני חי בריבוע לבחינת השערות מאפשרים לנתח נתונים קטגוריים. הם כוללים מבחן לטיב התאמה, שבודק האם הנתונים הנצפים תואמים התפלגות צפויה, ומבחן לאי תלות, שבודק קשרים פוטנציאליים בין שני משתנים קטגוריים. במדריך זה הסברנו את הדרך לערוך את המבחנים תוך שנעזרנו בשפת התכנות פייתון.

אולי גם זה יעניין אותך?

מבחן t-test לבחינת השערות

מבחן ANOVA - האם ממוצעי קבוצות שונים סטטיסטית

באיזה מבחן סטטיסטי להשתמש?

לכל המדריכים בנושא של למידת מכונה

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים