מדדים להערכת המודל ועקומת ROC-AUC

אחרי שבמדריך קודם הסברנו את הנושא של confusion matrix ומדדים להערכת המודל בלי להשתמש בקוד, במדריך זה נחזור לעסוק בנושא באמצעות דוגמה קונקרטית ומודל למידת מכונה מבוסס פייתון.

במדריך נכיר מדדים נוספים להערכת המודל, ונלמד על על עקומת ROC ומדד AUC.

מדדים להערכת המודל מאפשרים לנו לבחור את הפרמטרים ואת המודלים הטובים ביותר בהתאם למקרה שאותו אנו מנתחים.

פיתחתי את הקוד על סביבת Colab, המודל מבוסס TensorFlow והקוד כתוב בפייתון.

להורדת המחברת עם הקוד המלא בפורמט Jupyter notebook

הספריות

import numpy as np
import pandas as pd

from sklearn import metrics

import matplotlib.pyplot as plt
import seaborn as sns

• numpy ,pandas - בשביל החישובים
• sklearn.metrics בשביל המדדים להערכת המודל.
• Matplotlib ו-Seaborn בשביל התרשימים.

TensorFlow היא ספרייה של Google ללמידת מכונה:

import tensorflow as tf

מהי הגרסה?

tf.__version__

2.2.0

מסד הנתונים

מסד הנתונים במדריך הוא churn dataset המכיל מידע אודות לקוחות החברה Telco. המטרה שלנו היא לפתח מודל שיחזה איזה לקוחות עלולים לעזוב את החברה כדי לסייע להנהלה במניעת הבעיה שגורמת לחברה להפסיד הרבה כסף.

את מסד הנתונים הורדתי מ-GitHub (להורדת מסד הנתונים), וטענתי לתוך data frame של Pandas:

# load the dataset
df = pd.read_csv('Telco_customer_churn.csv')

נסקור את מסד הנתונים:

# explore
df.head()

כמה עמודות ושורות?

df.shape

(7043, 21)

המידע אודות הלקוחות כולל: מין, סוג השירות (טלפוניה, אינטרנט), משך זמן המנוי, שיטת התשלום והאם נטש את שירותי החברה - churn - בשפתם של אנשי המכירות.

במחברת המצורפת אפשר לראות שרק 3 מתוך 21 עמודות הם מספריות וכל היתר קטגוריות. מכיוון שהמודלים שלנו אינם יודעים לעבוד עם נתונים שאינם מספריים נמיר את העמודות השמיות למספרים.

נסקור את העמודה Churn אותה אנו מעוניינים שהמודל יחזה:

# what are the labels for the 'Churn' column?
df.Churn.unique()

array(['No', 'Yes'], dtype=object)

• עמודה קטגורית עם שני ערכים: Yes ,No. נשאר או נטש.

מהי התפלגות הנתונים?

# what's the class distribution?
df.Churn.value_counts()

No     5174
Yes    1869
Name: Churn, dtype: int64

• למעלה מ-73% מהלקוחות נשארו עם החברה. לפיכך, סט הנתונים אינו מאוזן.

הכנת הנתונים ללמידת מכונה

במחברת המצורפת אפשר לראות את הפעולות שעשית כדי להכין את הנתונים ללמידת מכונה. בקצרה:

1. ניקיתי את הנתונים.
2. הפכתי את העמודות הקטגוריות למספריות בשיטת one-hot encoding.
3. כתוצאה מקידוד one-hot קיבלתי שתי עמודות Churn בשם: Churn_Yes ו-Churn_Yes. את שמות העמודות החלפתי ל Left ו-Stayed.
4. הפרדתי את העמודות שאותם אנו מנסים לחזות: Left ו-Stayed מכל יתר המשתנים הבלתי תלויים עליהם יתבסס החיזוי.
5. הפרדתי לקבוצות אימון ובקרה.

בניית מודל למידת מכונה באמצעות TensorFlow

את המודל אני בניתי באמצעות TensorFlow.

נייבא את התלויות:

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Activation
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.callbacks import EarlyStopping

נבנה את המודל בהתאם לעקרונות המוסברים במדריך סיווג לקבוצות באמצעות למידת מכונה:

# build the model
model = Sequential()

# the first layer receives 45 input features and outputs 64 to the next layer
# the activation function 'relu' is the standard in the literature
model.add(Dense(64, input_shape=(45,), activation='relu'))

# the hidden layer has less units because that's a common practice
# to architect the hidden layers as a funnel
# it is also common that the number of neurons in a hidden has a power of 2
model.add(Dense(16, activation='relu'))

# the third layer outputs 2 classes as the number of categories 
# because it is categorical we use the softmax activation function
model.add(Dense(2, activation='softmax'))

• המודל מורכב מ-3 שכבות: קלט, שכבה חבויה ופלט.
• שכבת הקלט כוללת 45 קלטים כמספר העמודות הבלתי תלויות.
• בנוסף, שכבת הקלט כוללת 64 יחידות חישוב.
• relu היא פונקצית האקטיבציה ברירת המחדל.
• השכבה החבויה כוללת 16 יחידות חישוב.
• שכבת הפלט כוללת 2 פלטים כמספר התוצאות האפשריות - עזב או נשאר בחברה.
• פונקצית האקטיבציה softmax משמשת בשכבת הפלט לצורך סיווג. במקרה זה, סיווג בינארי.

את הארכיטקטורה של המודל קבעתי בצורה ניסיונית כפי שהסברתי במדריך בחירת ההיפר פרמטרים ללמידת מכונה.

נאמן את המודל:

# 1. Compile
# The categorical_crossentropy loss function is the one we 
# use when working with categorical labels
# the adam optimizer and accuracy as a metrics are standard
model.compile(optimizer='adam', 
              loss='categorical_crossentropy', 
              metrics=['accuracy'])
              
# 2. Define early stopping function
es = EarlyStopping(monitor='val_loss', patience=2)

# 3. Train
model.fit(X_train, y_train, 
          validation_data=(X_test,y_test), 
          batch_size=32, 
          callbacks=[es],
          epochs=100)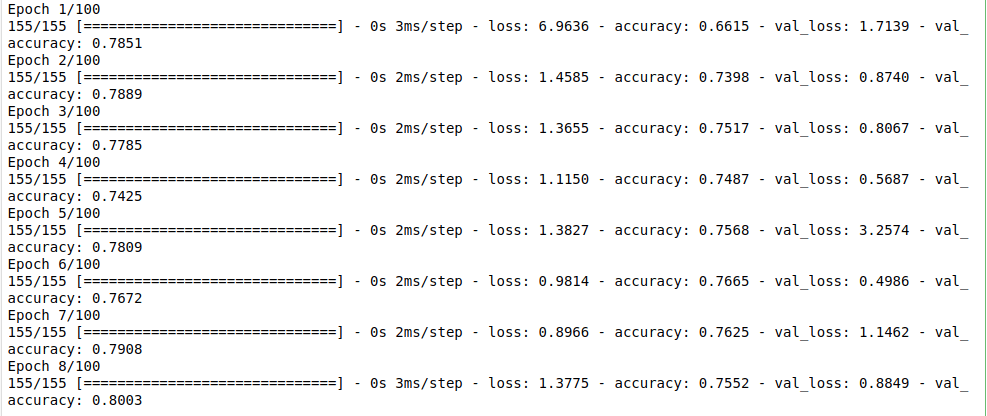

הערכת המודל

המדד הפשוט ביותר להערכת המודל הוא accuracy - החלק של הדוגמאות שהמודל סיווג נכונה.

ל-TensorFlow יש פונקציה שאומדת את המדד:

# find the accuracy with TensorFlow
loss, acc = model.evaluate(X_test, y_test)

67/67 [======] - 0s 1ms/step - loss: 0.8849 - accuracy: 0.8003

• שיעור הדוגמאות שהמודל הצליח לסווג הוא 80% ולכן נראה שהמודל מצליח בסיווג.

לפני שאנחנו ממהרים לפתוח את בקבוקי השמפניה, נשווה עם ה- null accuracy - שיעור הדיוק של מודל שב-100% מהמקרים חוזה את הסוג הנפוץ ביותר.

נחשב את ה-null accuracy במספר דרכים.

נתחיל בהצגת התפלגות התגיות:

# to see the class distribution
y_test.Stayed.value_counts()

1    1552
0     561

• 1552 לקוחות נשארו בחברה בעוד 561 עזבו.

מכיוון שהתגית הנפוצה יותר מונה 1552 דוגמאות נחלק מספר זה במספר הכולל של הדוגמאות כדי לקבל את ה-null accuracy:

# 1 is the most abundant
# so our null accuracy
# is the ratio of 1s
# or
1552 / (1552 + 561)

ה-null accuracy הוא:

0.73450070989115

שיטת חישוב זו נותנת תוצאה זהה לחישוב ממוצע העמודה:

# which is equivalent to
y_test.Stayed.mean() # 0.73450070989115

• בגלל שממוצע העמודה הוא סכום העמודה מחולק במספר הדוגמאות, והדוגמאות בקידוד one-hot יכולות לקבל את הערך 1 או 0.

נשתמש באותו אמצעי כדי לחשב את יחס העמודה הפחות נפוצה:

# the ratio of 'Left'
y_test.Left.mean() # 0.26549929010885

מכיוון ש- null accuracy הוא היחס של התגית הנפוצה ביותר אנחנו יכולים להשתמש בפונקציה הפייתונית max() כדי למצוא את איזה מהיחסים עבור התגיות השונות הוא הגבוה ביותר:

# the null accuracy is the ratio of the most abundant class
# here we use max to find the highest ratio
max(y_test.Stayed.mean(), y_test.Left.mean()) # 0.73450070989115

ה-accuracy הוא 80% והוא מאוד קרוב ל- null accuracy של 73%. מה שאומר שהמודל פחות מוצלח ממה שחשבנו כשרק קיבלנו את התוצאות.

מכך, אנו יכולים ללמוד שבכל פעם שאנחנו משתמשים ב-accuracy עלינו להשוות את התוצאה עם ה-null accuracy.

מה המודל חוזה באמת?

עד עכשיו ראינו שהמודל חוזה תגיות אבל מה שהמודל מנפק באמת הם הסבירויות שהדוגמה שייכת לאחת התגיות.

נשתמש במתודה predict() של TensorFlow כדי להציץ בסבירויות שהמודל חוזה עבור השתייכות כל אחת מהדוגמאות לאחת התגיות:

y_pred_probabilities = model.predict(X_test)

נביט בתוצאה עבור 10 הדוגמאות הראשונות:

# the first 10 predictions
y_pred_probabilities[:10, :]

array([[9.99836087e-01, 1.63871722e-04],
       [8.81925106e-01, 1.18074894e-01],
       [9.81377780e-01, 1.86222643e-02],
       [1.83865249e-01, 8.16134691e-01],
       [9.99996424e-01, 3.54904614e-06],
       [8.60354543e-01, 1.39645532e-01],
       [6.71267748e-01, 3.28732282e-01],
       [1.00000000e+00, 1.31343159e-09],
       [1.00000000e+00, 4.53645210e-09],
       [9.99884844e-01, 1.15129718e-04]], dtype=float32)

• כל פריט במערך מייצג דוגמה אחת.
• כל פריט הוא מערך המכיל שני ערכים: אינדקס 0 ו-1 כי יש לנו שתי דוגמאות.
• סכום ההסתברויות של כל פריט שווה ל-1.
• המודל לוקח את ההסתברות הגבוהה ביותר של כל דוגמה כדי לקבוע את הסיווג.

אנחנו יכולים לחקות את הדרך שבה המודל מסווג באמצעות הפונקציה Numpy.argmax() שמציגה את מיקום האינדקס של הגבוה מבין הערכים:

# use np.argmax to emulate the way that the model classifies
np.argmax(y_pred_probabilities[:10, :], axis=1)

array([0, 0, 0, 1, 0, 0, 0, 0, 0, 0])

אפשר להגיע לאותה תוצאה גם בדרך אחרת.

אם יש לנו שתי אפשרויות לסיווג אז הערך הגבוה יותר בכל דוגמה חייב להיות גבוה מ-0.5:

y_pred_classes = (y_pred_probabilities[:, 1] > 0.5).astype(int)

עד עכשיו ראינו שצריך להיזהר כשמסמתכים רק על accuracy כדי להעריך את ביצועי המודל וגם שהמודל המסווג מנפק הסתברויות של הסיווגים השונים. בחלק הבא נייצר confusion matrix ממנה נגזור מדדים שונים להערכת המודל.

Confusion matrix ומדדים להערכת המודל

אחרי שהרצנו את המודל שאלה מעניינת ביותר היא עד כמה הוא טוב. תשובה אחת שראינו משתמשת במדד accuracy, החלק היחסי של דוגמאות שהמודל הצליח לסווג נכונה. הבעיה עם המדד שהוא אינו יודע להגיד לנו אילו שגיאות המודל עשה. בנוסף, המדד מאבד מיעילותו כאשר סט הנתונים אינו מאוזן. כדי לחשב מדדים נוספים להערכת המודל נצטרך ליצור טבלת confusion matrix עליה נבסס מגוון של מדדים.

במדריך Confusion matrix ומדדים להערכת המודל הסברתי את הנושא באופן אינטואטיבי וללא קוד. במדריך זה אני חוזר לעסוק בנושא באופן קונקרטי יותר ובליווי דוגמאות קוד.

הפונקציה plot_confusion_matrix() תצייר בשבילנו את ה- Confusion matrix על פי הסיווג שעשה המודל שלנו:

def plot_confusion_matrix(cf_matrix): 
    print('Confusion Matrix')
    
    ax= plt.subplot()
    sns.heatmap(cf_matrix, annot=True, ax = ax, fmt='d', cmap='Blues', cbar=False)

    # labels, title and ticks
    ax.set_title('Confusion Matrix')
    ax.set_xlabel('Predicted labels')
    ax.set_ylabel('Actual labels')
    ax.xaxis.set_ticklabels(['Stayed', 'Left']) 
    ax.yaxis.set_ticklabels(['Stayed', 'Left'])

• את הפרמטר שמקבלת הפונקציה plot_confusion_matrix() תייצר הפונקציה metrics.confusion_matrix():

cf_matrix = metrics.confusion_matrix(y_test.Left, y_pred_classes)

plot_confusion_matrix(cf_matrix)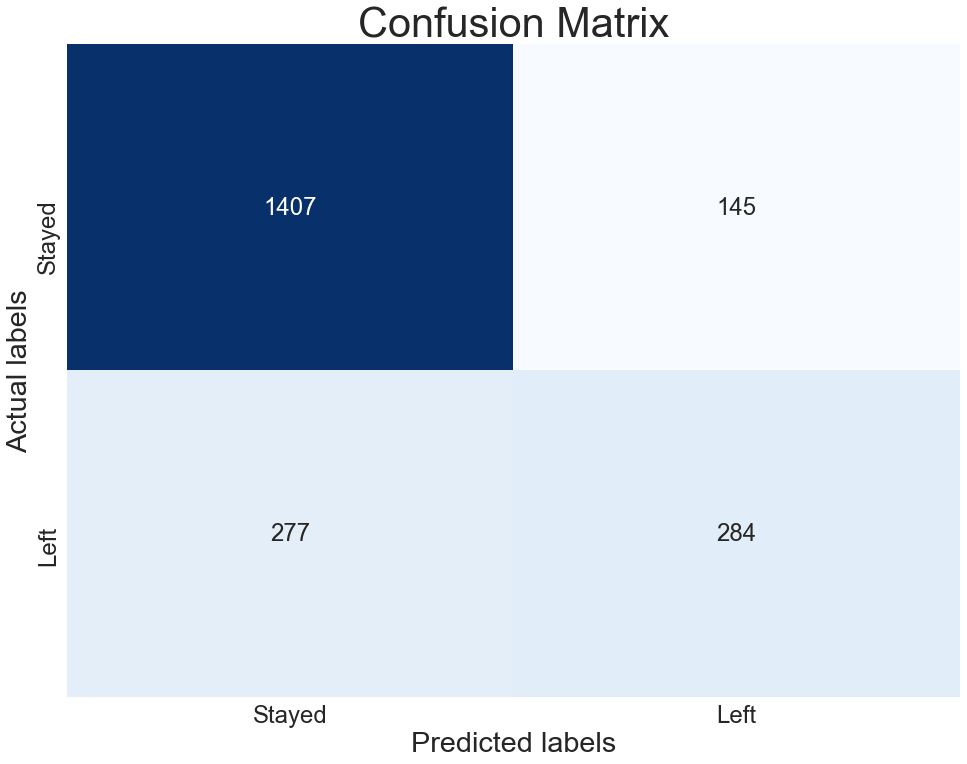

• כל תא בטבלה מכיל את מספר אחד מסוגי הסיווגים שהמודל יכול לעשות.
• העמודות מציגות את התגיות שסיווג המודל, והשורות את הסיווג בפועל.
• הטבלה היא מטריצה של 2x2 בגלל שבמקרה שלנו קיימות רק שתי אפשרויות – עזב את החברה או נשאר.
• כל דוגמה יכולה להמצא רק באחד התאים.

בגלל שאנחנו עובדים על סיווג בינארי (2 תגיות אפשריות) לכל אחד מהתאים יש שם.

לפני שאנחנו יכולים לתת את השמות אנחנו צריכים לקבוע איזה סיווג הוא חיובי.

במקרה שלנו, התגית החיובית היא "עזב את החברה" (Left) כי המטרה שלנו היא לצמצם את שיעור הנטישה.

ועכשיו, נכנה כל אחד מהתאים בשם:

• True Positives (TP) - המודל חזה נכונה את העוזבים את החברה.
• True Negatives (TN) - המודל חזה נכונה את מי שנשאר בחברה.
• False Positives (FP) - המודל שגה וזיהה בטעות לקוח שנשאר בחברה כמי שעומד לעזוב.
• False Negatives (FN) - המודל שגה וזיהה בטעות לקוח שנטש כמי שצפוי להישאר בחברה.

הוספתי על גבי התרשים את שמות התאים:

המדדים להערכת המודל נגזרים מתוך הערכים בטבלה. נבודד את הערך של כל תא בטבלה לתוך משתנה באמצעות הפונקציה הבאה:

def get_confusion_matrix_cells(cf_matrix) :
    TN = cf_matrix[0, 0]
    FP = cf_matrix[0, 1]
    TP = cf_matrix[1, 1]
    FN = cf_matrix[1, 0]
    return TN, FP, TP, FN

נמצה את הערכים מתוך הטבלה:

TN, FP, TP, FN = get_confusion_matrix_cells(cf_matrix)

המדד הראשון אותו נחשב הוא accuracy - שיעור התוצאות שהמודל סיווג נכונה:

# what's the calculated accuracy?
(TP + TN) / (TP + TN + FN + FP)

0.8002839564600095

ניתן לחשב את ה-accuracy גם באמצעות הפונקציה metrics.accuracy_score() שמקבלת שני פרמטרים. הראשון, תגיות האמת. השני, התגיות שהמודל חזה:

# another way to find the accuracy
# first param is the actual values
# the second are the predicted ones
metrics.accuracy_score(y_test.Left.values, y_pred_classes)

0.8002839564600095

• סדר ההזנה של הפונקציות השייכות לקלאס metrics של sklearn הוא חשוב. הפרמטר הראשון הוא נתוני האמת, והפרמטר השני הוא הסיווגים שחזה המודל.

מדד חשוב נוסף הוא הרגישות Sensitivity - היחס של סיווגי אמת עבור דוגמאות שהם חיוביות במציאות.

הנוסחה לחישוב Sensitivity:

# sensitivity - the proportion of positives 
# that are correctly identified
TP / (TP + FN)

תיתן לנו את היחס הבא:

0.5062388591800356

שמות נוספים ל- Sensitivity הם True Positive Rate ו- Recall.

דרך חלופית לחישוב ה-Sensitivity היא באמצעות הפונקציה metrics.recall_score() של sklearn:

metrics.recall_score(y_test.Left.values, y_pred_classes, pos_label=1)

0.5062388591800356

המדד Specificity הוא היחס של סיווגי אמת עבור דוגמאות שהם שליליות במציאות.

הנוסחה לחישוב Specificity:

# specificity - the proportion of negatives 
# that are correctly identified
TN / (TN + FP)

תיתן לנו את היחס הבא:

0.9065721649484536

הערכים של המדדים נעים בין 0 ל-1. מכיוון שערך ה- Specificity הוא 0.9 וערך ה- Sensitivity הוא רק 0.5 אנחנו יכולים לאמר שהמודל הוא ספציפי אבל לא רגיש.

המשמעות של ערך Specificity גבוה היא שהמודל מצליח לזהות נכונה את הלקוחות שישארו בחברה.

המשמעות של ערך Sensitivity נמוך היא שהמודל מתקשה לזהות את הלקוחות שעומדים לעזוב את החברה.

הבעיה שלנו היא שאנחנו רוצים לזהות דווקא את אילה שעומדים לעזוב, ולכן אנחנו צריכים למצוא דרך להגביר את רגישות המודל.

דרך אחת להגביר את רגישות המודל היא להוריד את הסף שמעליו המודל מזהה לקוח כמי שעומד לעזוב.

ראינו שהמודל מניח שערך הסף הוא 0.5 אבל במקרה שלנו כדאי לנו להפחית את הסף כדי לתפוס בזמן את הלקוחות שעלולים לעזוב.

נוריד את הסף מ-0.5 ל-0.4:

y_pred_classes04 = (y_pred_probabilities[:, 1] > 0.4).astype(int)

ונשרטט את ה-confusion matrixהמתארת את הסיווגים החדשים:

cf_matrix04 = metrics.confusion_matrix(y_test.Left, y_pred_classes04)

plot_confusion_matrix(cf_matrix04)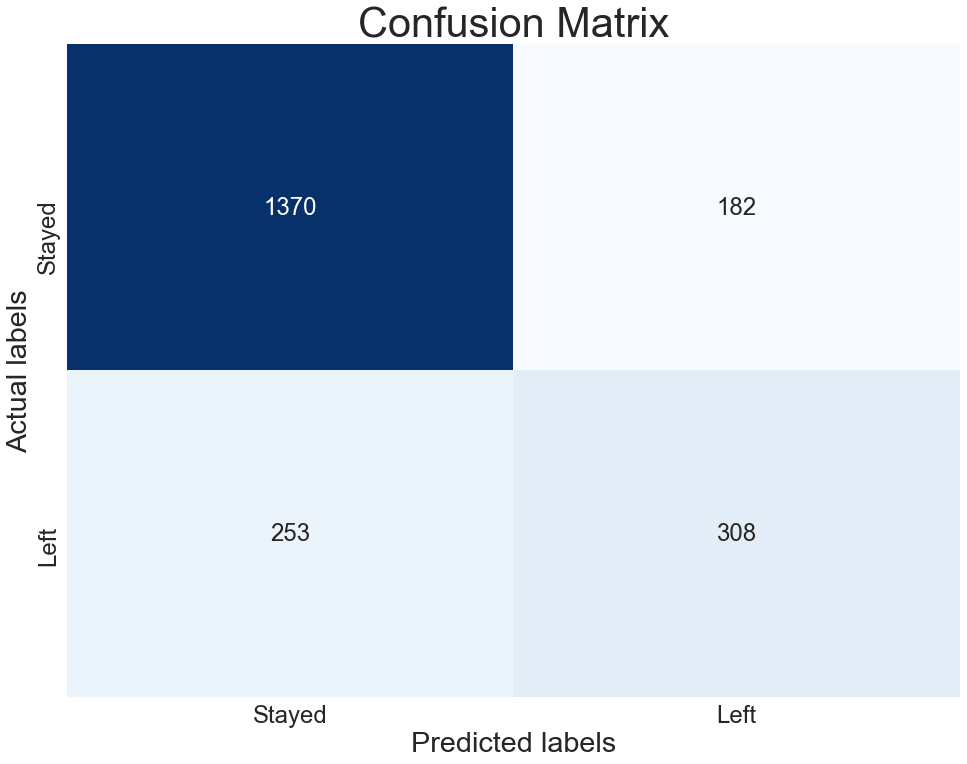

• אנחנו יכולים לראות שהסיווגים עברו ימינה עם יותר דוגמאות שהמודל מסווג כ- ’Left’.

נוריד את הסף עוד יותר, והפעם ל-0.25:

y_pred_classes025 = (y_pred_probabilities[:, 1] > 0.25).astype(int)

cf_matrix025 = metrics.confusion_matrix(y_test.Left, y_pred_classes025)

plot_confusion_matrix(cf_matrix025)

• הורדת הסף מ-0.4 ל-0.25 גרמה לעוד יותר תוצאות להיות מסווגות כחיוביות. כולל הגדלת מספר ה-false positive והקטנת מספר ה-false negative.

נחשב את המדדים עבור רמת סף 0.25:

TN025, FP025, TP025, FN025 = get_confusion_matrix_cells(cf_matrix025)

מה ה-accuracy?

# what's the accuracy?
(TP025 + TN025) / (TP025 + TN025 + FN025 + FP025)

0.7789872219592996

מה ה-sensitivity?

# what's the sensitivity?
TP025 / (TP025 + FN025)

0.6131907308377896

מה ה-specificity?

# what's the specificity?
TN025 / (TN025 + FP025)

0.8389175257731959

• הרגישות גברה בעוד הספציפיות ירדה בגלל שיותר דוגמאות סווגו כחיוביות.
• לפני הפחתת רמת הסף יותר דוגמאות סווגו כשליליות. בהתאם, הרגישות היתה נמוכה והספיצפיות גבוהה.
• מכך אנו יכולים להסיק על קשר הפוך בין ספציפיות ורגישות.

הפחתת רמת הסף לסיווג גרמה למודל רגיש יותר שמצליח לזהות יותר לקוחות שעומדים לעזוב. לאותם לקוחות אפשר לתת הטבות כדי שישארו, וימשיכו לשלם. מצד שני, הספציפיות המופחתת פירושה שיותר לקוחות שלא רוצים לעזוב יזוהו כמי שעלולים לעזוב אבל זו בעיה קטנה כי שום אסון לא יקרה אם החברה תעניק הטבה בטעות.

עד עכשיו ניחשנו את רמות הסף השונות שמעליהם נקבל רגישות או ספציפיות בהתאם לבעיה שעל הפרק. האם קיימת שיטה למציאת הסף?

עקומת ROC ויחס AUC

עקומת ROC – AUC מתארת את יכולתו של מודל מסווג להבחין בין שתי קטגוריות עבור רמות סף שונות.

נשתמש בעקומת ROC – AUC כדי לאתר את רמת הסף שנותנת לנו את המידה הרצויה של רגישות וספציפיות.

הפונקציה metrics.roc_curve() מקבלת בתור פרמטרים את סיווגי האמת ואת הסתברות הערכים החזויים ומחזירה שלוש סדרות מספרים:

• False Positive Rate השווה ל 1 - Specificity
• True Positive Rate שהוא שם נרדף ל- Sensitivity
• thresholds סידרה של רמות סף

fpr, tpr, thresholds = metrics.roc_curve(y_test.Left, y_pred_probabilities[:, 1])

נשתמש בערכים שחישבה הפונקציה כדי לשרטט את עקומת ה-ROC:

plt.plot(fpr, tpr)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.title('ROC curve')
plt.xlabel('False Positive Rate (1 - Specificity)')
plt.ylabel('True Positive Rate (Sensitivity)')
plt.grid(True)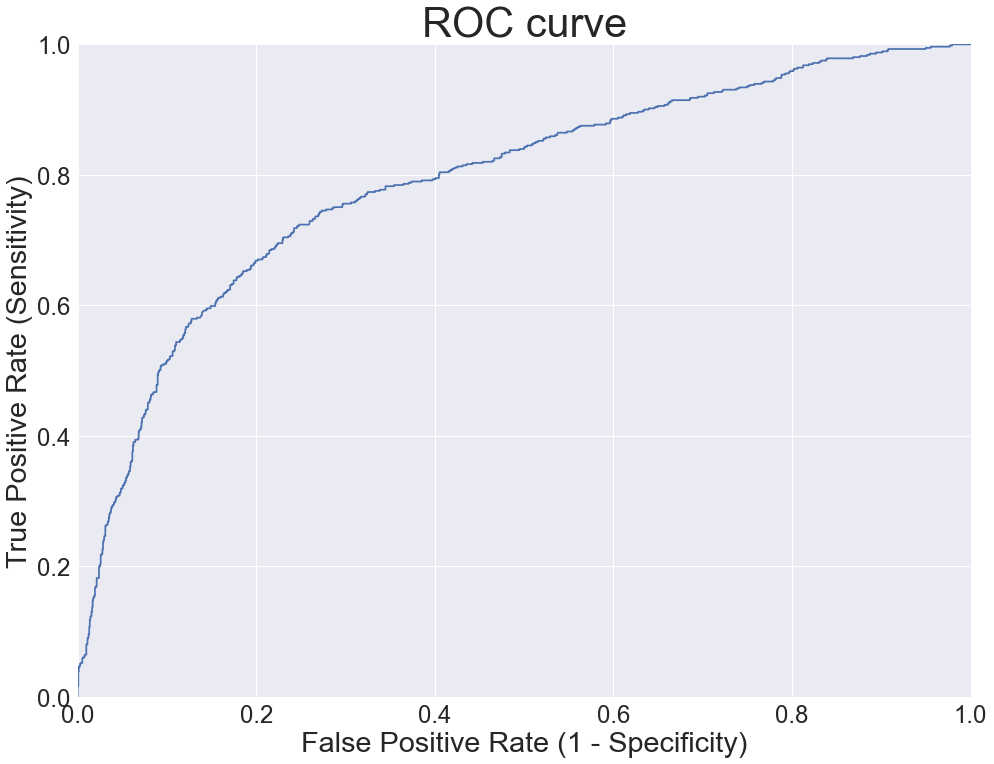

• העקומה מתארת את הרגישות כנגד 1- Specificity עבור רמות סף שונות.
• במקרה שלנו אנחנו יכולים לראות שכדי לקבל רגישות של 0.8 נצטרך להסתפק בספציפיות של 0.6
• עקומה אידיאלית תשיק לדפנות השמאלית והעליונה של הגרף כי היא תייצג מודל שהוא ספציפי ורגיש.

מהעקומה אנחנו לא יכולים לראות ישירות את רמות הסף אז נתחיל מבניית Panda’s DataFrame ששלוש העמודות בה הם סדרות המספרים שפלטה הפונקציה metrics.roc_curve():

df = pd.DataFrame({'THRESHOLDS': thresholds,'FPR':fpr, 'TPR':tpr})

ועכשיו אפשר לחתוך את ה-DataFrame עד שנמצא את הסף שמעניין אותנו. לדוגמה, סף של 0.5:

אחרי שקצת שחקתי הגעתי לתוצאה הבאה:

print(df.iloc[184:194])

THRESHOLDS       FPR       TPR
184    0.513828  0.091495  0.500891
185    0.510863  0.092784  0.500891
186    0.501709  0.092784  0.506239
187    0.501400  0.093428  0.506239
188    0.498219  0.093428  0.508021
189    0.495354  0.096005  0.508021
190    0.494241  0.096005  0.509804
191    0.482263  0.098582  0.509804
192    0.478983  0.098582  0.511586
193    0.478164  0.099227  0.511586

• סף של 0.5 נמצא בין הפריטים 187 ל-188.
• אנחנו יכולים לראות שהערכים הם לא בהכרח ערכי הסף המדויקים אלא ערכים קרובים מספיק.

נעשה את זה יותר שיטתי.

את הפונקציה הבאה נזין בערך הסף המבוקש והיא תמצא בתוך ה- DataFrame את ערך הסף הקרוב ביותר ואת ערכי הרגישות והספציפיות המתאימים.

def get_metrics_by_threshold(th) :
    row = df.iloc[(df['THRESHOLDS']-th).abs().argsort()[:1]]
    print('Sensitivity: ', row.TPR.values[0])
    print('Specificity: ', 1 – row.FPR.values[0])

נבחן את ערכי הספציפיות והרגישות עבור שלושה ערכי סף שונים:

get_metrics_by_threshold(0.75)

Sensitivity:  0.33689839572192515
Specificity:  0.9445876288659794

get_metrics_by_threshold(0.5)

Sensitivity:  0.5062388591800356
Specificity:  0.9065721649484536

get_metrics_by_threshold(0.25)

Sensitivity:  0.6131907308377896
Specificity:  0.8402061855670103

• אנחנו רואים את השפעת ערך הסף על הרגישות והספציפיות. ככל שערך הסף יורד, עולה הרגישות וגם פוחתת הספציפיות.

יחס AUC

בחלק הקודם של המדריך למדנו על עקומת ROC שמראה לנו את היחס בין ספציפיות ורגישות ברמות סף שונות אבל יש לה תכונה נוספת מעניינת מפני שככל שהמודל המסווג הוא טוב יותר כך השטח מתחת לעקומה יהיה גדול יותר כי העקומה תשיק לדפנות השמאלית והעליונה של הגרף הודות לרגישות וספציפיות גבוהות.

השטח מתחת לעקומה מכונה AUC (Area Under the Curve) וכלל שערכו גבוה יותר כך המודל נחשב לטוב יותר. כשהערך הגבוה ביותר של AUC הוא 1.

נחשב את הערך:

metrics.auc(fpr, tpr)

0.7901350910561037

אנחנו יכולים להשתמש ב- AUC כדי להשוות בין מודלים ולבחור את המודל המוצלח ביותר. אפילו אם סט הנתונים אינו מאוזן.

סיכום

קיימות דרכים רבות להעריך את ביצועי המודל המסווג:

accuracy הוא המדד הפשוט ביותר אבל אם משתמשים בו אז חשוב להשוות ל-null accuracy.

על בסיס ה- confusion matrix אנחנו יכולים לחשב מגוון של מדדים כתלות בבעיה שבה אנו עוסקים.

בנוסף, confusion matrix יכולה לשמש מודלים שמסווגים מספר קטגוריות ולא רק בינאריים.

בניגוד ל-confusion matrix, עקומת ROC – AUC אינה מחייבת את בחירת רמת הסף מראש וניתן להשתמש בה גם כאשר הקטגוריות אינן מאוזנות אך קשה יותר לעבוד איתה במקרים של סיווגים שאינם בינאריים.

שילוב של מדדים להערכת המודל מבוססי confusion matrix ו ROC – AUC יכולים לעזור רבות בניתוח הנתונים, ועל כן כדאי לשלב ביניהם כמה שאפשר.

לכל המדריכים בסדרה על לימוד מכונה

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים