רווח בר סמך confidence interval

סטטיסטיקה עוסקת בהערכה של פרמטרים באוכלוסייה דוגמת ממוצע או שונות. כאשר לרוב קשה ואף בלתי אפשרי למדוד את כלל האוכלוסיה, ולכן משתמשים בדגימות. לדוגמה, אם אנחנו מעוניינים בגובה הממוצע של הנשים בישראל אז ניקח דגימה אקראית ומייצגת של 5 נשים וממנה נעריך את גובהן הממוצע של נשים בכלל האוכלוסייה.

להלן דוגמה של תוצאות של מדגם להערכת גובהם של נשים בישראל במטרים:

sample = [1.67, 1.55, 1.63, 1.69, 1.72]

נחשב את הממוצע של המדגם בעזרת פייתון:

import numpy as np

sample = [1.67, 1.55, 1.63, 1.69, 1.72]

# Convert the sample to a NumPy array
sample_array = np.array(sample)

# Calculate the mean using NumPy's mean function
mean_value = np.mean(sample_array)

print("The mean of the sample is:", mean_value)

ממוצע המדגם המחושב הוא 1.652 מטר. כאשר הממוצע המחושב מהמדגם הוא רק הערכה לגובה הממוצע באוכלוסייה.

הפרמטר הסטטיסטי המחושב מהמחקר הוא רק קירוב לערך באוכלוסייה כולה.

בגלל שהממוצע המחושב מהמדגם הוא רק הערכה רצוי להגדיר טווח בתוכו עשוי להימצא בסבירות רבה הממוצע של האוכלוסיה כולה כדי שנוכל לומר משהו כמו "על סמך תוצאות המדגם אנחנו יכולים להיות בטוחים ב-95% שממוצע האוכלוסייה כולה נמצא בטווח שבין ערך מינימלי וערך מקסימלי". לדוגמה, "על סמך תוצאות המדגם להערכת גובהם של נשים בישראל אנחנו יכולים להיות בטוחים ב-95% שגובהם של נשים ישראליות הינו בין 1.57 ל-1.74".

הטווח בתוכו אנו מעריכים שנמצא הממוצע נקרא רווח בר-סמך (confidence interval או בקיצור CI). בחלקו הבא של המדריך נלמד כיצד לחשב אותו.

הטווח בתוכו אנו מעריכים שנמצא הפרמטר הסטטיסטי נקרא רווח בר-סמך.

איך לחשב רווח בר סמך?

ניתן לחשב רווח בר-סמך עבור כל פרמטר באוכלוסייה, כגון שונות, פרופורציה או ממוצע. חישוב רווח בר-סמך מאפשר לנו להעריך טווח שבו נמצא הפרמטר האמיתי באוכלוסייה ממנה לקחנו את המדגם ברמת ביטחון רצויה (לרוב, 95%).

הנוסחה לחישוב רווח בר-סמך לממוצע הינה:

$$ CI(mean) = \overline{x} \pm t_{\frac{\alpha}{2}, n-1} \cdot \frac{s}{\sqrt{n}} $$

נסביר את הפרמטרים בנוסחה:

• x̄: ממוצע המדגם, המשמש להערכת ממוצע האוכלוסייה (μ).

• s: שונות המדגם. ככל שהשונות גדלה, כך גדל רווח בר-סמך. הסיבה לכך היא ששונות גבוהה מצביעה על פיזור נתונים גדול יותר באוכלוסייה, ולכן אנו זקוקים לטווח רחב יותר כדי להבטיח רמת ביטחון גבוהה בהערכה שלנו.

• n: גודל המדגם. ככל שגודל המדגם גדל, כך קטן רווח בר-סמך. הסיבה לכך היא שמדגם גדול יותר מספק מידע מדויק יותר על ממוצע האוכלוסייה.

• את הרווח בר-סמך אנחנו מבססים על שגיאת התקן של הממוצע:

  $$ SEM = \frac{s}{\sqrt{n}} $$

• t: צורת ההתפלגות היא בהתאם להתפלגות t כאשר רוב הסיכויים שהפרמטר נמצא קרוב למרכז וככל שאנחנו מתרחקים לשוליים כך קטנה ההסתברות.

  בנוסחה אנחנו רואים df שמציין את מספר דרגות החופש כי צורת ההתפלגות משתנה בהתאם למספר דרגות החופש (מספר הפריטים במדגם פחות 1).

  את הערכים התוחמים את הרווח בר-סמך קובעת רמת המובהקות α.

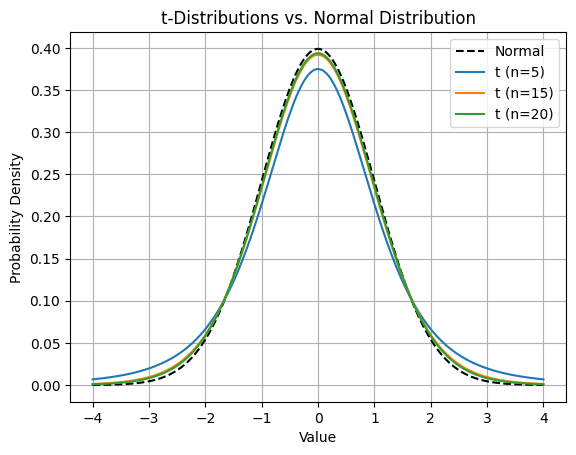
הנתונים מתפלגים בהתאם להתפלגות t שצורתה מדמה את ההתפלגות הנורמלית עם שוליים גבוהים יותר עבור מדגמים קטנים יותר.

קוד הפייתון להלן מדגים את השתנות התפלגות t על פי גודל המדגם ומספר דרגות החופש:

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t, norm

# Degrees of freedom for each sample size
degrees_of_freedom = [4, 14, 19] 

# Range of values for plotting
x = np.linspace(-4, 4, 200)

plt.plot(x, norm.pdf(x), color='black', linestyle='--', label='Normal')

# Plot t-distributions for different sample sizes
for df in degrees_of_freedom:
   y = t.pdf(x, df)
   label_text = 't (n={})'.format(df+1)
   plt.plot(x, y, label=label_text)

plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.title('t-Distributions vs. Normal Distribution')
plt.legend()
plt.grid()
plt.show()

בשביל הרווח בר סמך אנחנו לא לוקחים את כל ההתפלגות אלא משאירים רווח לטעות. כאשר רמת המובהקות α היא ההסתברות שאנחנו מוכנים להסתכן בה שההערכה שלנו תהיה שגויה לרוב, α=5%.

הגרף הבא מציג רווח בר סמך על גבי העקומה שיוצרת התפלגות t:

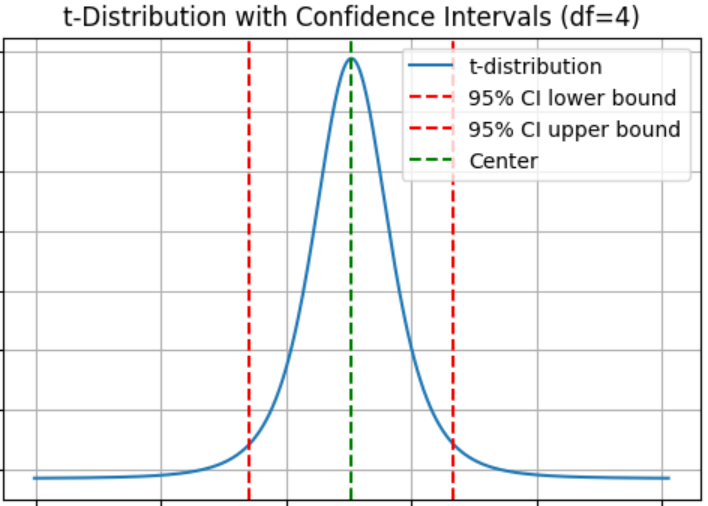
• ההתפלגות הינה התפלגות t אשר צורתה תלויה במספר דרגות החופש.
• במרכז ההתפלגות נמצא הממוצע (קו ירוק מקווקו).
• משני צידיו של הממוצע נמצאים קווים אדומים מקווקוים אשר מציינים את מיקום גבולות הרווח בר-סמך.
• בגלל שבחרנו ברמת מובהקות α=5% גבולו הנמוך (השמאלי) של הרווח בר-סמך נמצא ב-x=2.5% וגבולו העליון (הימני) נמצא ב-x=97.5%.

נחזור לנוסחה ולנתוני הגובה של 5 נשים ישראליות כדי לחשב באופן ידני את הרווח בר-סמך:

1. ראשית, נמצא את ממוצע המדגם :

   $$ \bar{x} = \frac{\sum x_i}{n} = \frac{167 + 155 + 163 + 169 + 172}{5} = 165.2 $$

   כאשר:

   • (x_i) מייצג כל גובה בודד
   • (n) הוא מספר התצפיות (נשים במדגם)

2. קודם לחישוב שגיאת התקן נחשב את סטיית התקן.

   נחשב את סטיית התקן (σ) באמצעות הנוסחה:

   $$ \begin{aligned} &\sigma = \sqrt{\frac{\sum{(x_i - \bar{x})^2}}{n-1}} \\ \\ &= \sqrt{\frac{(167 - 165)^2 + (155 - 165)^2 + (163 - 165)^2 + (169 - 165)^2 + (172 - 165)^2}{5-1}} \\ \\ &= 6.57 \end{aligned} $$

   עכשיו, נחשב את שגיאת התקן של הממוצע (SEM) על סמך סטיית התקן:

   $$ SEM = \frac{s}{\sqrt{n}} = \frac{6.57}{\sqrt{5}} = 2.93 $$

3. על פי רמת המובהקות (במקרה שלנו כמו בד"כ α=0.05) נשלוף מהמחשב או מטבלאות סטטיסטיות את הערכים הקריטיים שערכם לקוח מהתפלגות t עבור דרגות החופש הדרושות (במקרה שלנו, המדגם כלל 5 פריטים ולפיכך 4 דרגות חופש). נשתמש לצורך החישוב בקוד הפייתון הבא:

   from scipy.stats import t
   
   alpha = 0.05
   sample_size = 5
   
   degrees_of_freedom = sample_size - 1
   critical_value = t.ppf(1 - alpha / 2, degrees_of_freedom)

   התוצאה היא: 2.78 היא הערך הקריטי.

4. את הערך הקריטי יש לחסר ולהוסיף לממוצע בשביל לקבל את גבולות הרווח בר-סמך. ערכים אילה יש לנרמל לערכים שמעניינים אותנו ולכן נכפיל אותם בשגיאת התקן:

   error = critical_value * SEM = 2.78 * 2.93 = 8.133

5. את גבולות הרווח בר-סמך נפחית ונוסיף לממוצע כדי לקבל את גבולות הרווח בר-סמך.

   גבול תחתון:

   $$ lower = \bar{x} - error = 165.2 - 8.1 = 157.1 $$

   גבול עליון:

   $$ upper = \bar{x} + error = 165.2 + 8.1 = 173.3 $$

ממוצע המדגם שכלל 5 פרטים שערכנו לצורך הערכת גובהם של נשים בישראל הוא 165.2 ס"מ וגבולות הרווח בר סמך כאשר רמת המובהקות הינה α=0.05 נמצאים במרחק 8.1 ס"מ לכל כיוון:

165.2 cm (95% CI, 157.1 to 173.3 cm)

• מסקנה: ממוצע האוכלוסייה סביר שיימצא בטווח שבין 157.1 ס"מ ו-173.3 ס"מ.

קוד הפייתון הבא מקבל כקלט את מערך הנתונים כאשר הפלט הוא הגבול העליון והתחתון של הרווח בר-סמך לממוצע:

import numpy as np
from scipy.stats import t


def calculate_confidence_interval(data, confidence_level=0.95):
     sample_mean = np.mean(data)
     sample_std = np.std(data, ddof=1)  # Sample standard deviation
     sample_size = len(data)

     degrees_of_freedom = sample_size - 1
     alpha = 1 - confidence_level
     critical_value = t.ppf(1 - alpha / 2, degrees_of_freedom)


     margin_of_error = critical_value * (sample_std / np.sqrt(sample_size))
  
     lower_bound = sample_mean - margin_of_error
     upper_bound = sample_mean + margin_of_error


     return lower_bound, upper_bound

נריץ את הפונקציה על נתוני המדגם שלנו עבור רמת מובהקות שהיא α=0.05:

# Given data
heights = np.array([167, 155, 163, 169, 172])

confidence_level = 0.95
print(f"CI = {calculate_confidence_interval(heights, confidence_level)}")

גבולות הרווח בר-סמך אותם מחשבת הפונקציה של פייתון הינם:

CI = (157.0389514321009, 173.36104856789908)

ייצוג גרפי של רווח בר-סמך

הגרף הבא מתאר את התוצאות אותם חישבנו בסעיף הקודם:

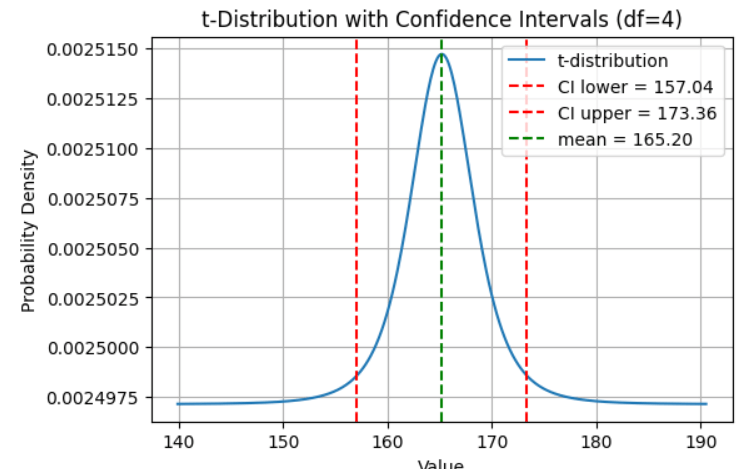
• בירוק ממוצע המדגם והוא נמצא בדיוק במרכז ההתפלגות. כאשר 95% מההתפלגות נמצאים בתוך גבולות הרווח בר סמך.
• בגלל איך שהרווח בר-סמך עובד (כפי שנראה בסעיף הבא) אנחנו יכולים להיות בטוחים ב-95% שממוצע האוכלוסייה נמצא בתוך גבולות הרווח בר-סמך.

קוד הפייתון הבא הוא זה שיצר את התיאור של הרווח בר-סמך:

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t

def calculate_mean(data):
    # Calculate sample mean
    return np.mean(data)

def calculate_confidence_interval(data, confidence_level=0.95):
    sample_mean = calculate_mean(data)
    
    sample_std = np.std(data, ddof=1)  # Sample standard deviation
    sample_size = len(data)

    degrees_of_freedom = sample_size - 1
    alpha = 1 - confidence_level
    critical_value = t.ppf(1 - alpha / 2, degrees_of_freedom)
   

    margin_of_error = critical_value * (sample_std / np.sqrt(sample_size))

    lower_bound = sample_mean - margin_of_error
    upper_bound = sample_mean + margin_of_error

    return lower_bound, upper_bound

def scale(val, scaling_factor, center):
    return val * scaling_factor + center

def rev_scale(val, scaling_factor, center):
    return (val - center) / scaling_factor

def plot_t_distribution_with_confidence_intervals(data, lower_x_boundary, upper_x_boundary):
    # Get the confidence interval boundaries
    ci_lower, ci_upper = calculate_confidence_interval(data)

    # Calculate the center as the mean of the confidence interval bounds
    center = (ci_lower + ci_upper) / 2

    degrees_of_freedom = len(data) - 1

    # Adjusted scaling factor for x-values
    scaling_factor = (upper_x_boundary - lower_x_boundary) / (ci_upper - ci_lower)

    # Reduce the number of points for the t-distribution
    x = np.linspace(lower_x_boundary, upper_x_boundary, 400)  # Adjust the number of points as needed

    # Generate scaled x and y values for the t-distribution
    y = scale(t.pdf(rev_scale(x, scaling_factor, center), df=degrees_of_freedom), scaling_factor, center)
    y /= y.sum()  # Normalize y-values to sum to 1

    # Reduce the figure size
    plt.figure(figsize=(6, 4))  # Adjust the figure size as needed
    plt.plot(x, y, label='t-distribution')

    # Plot vertical lines for confidence intervals
    plt.axvline(x=ci_lower, color='red', linestyle='--', label=f"CI lower = {ci_lower:.2f}")
    plt.axvline(x=ci_upper, color='red', linestyle='--', label=f"CI upper = {ci_upper:.2f}")

    # Plot horizontal line at the center
    plt.axvline(x=center, color='green', linestyle='--', label=f"mean = {center:.2f}")

    plt.xlabel('Value')
    plt.ylabel('Probability Density')
    plt.title(f't-Distribution with Confidence Intervals (df={degrees_of_freedom})')
    plt.legend()
    plt.grid(True)
    plt.show()


# Given data
heights = np.array([167, 155, 163, 169, 172])

print(f"x̄ = {calculate_mean(heights)}")


# Given data
heights = np.array([167, 155, 163, 169, 172])

confidence_level = 0.95
print(f"CI = {calculate_confidence_interval(heights, confidence_level)}")

lower_x_boundary, upper_x_boundary = calculate_confidence_interval(heights, .999)
plot_t_distribution_with_confidence_intervals(heights, lower_x_boundary, upper_x_boundary)

מה המשמעות של רווח בר-סמך?

כפי שראינו, רווח בר-סמך מחושב ממדגם ומספק טווח של ערכים שסביר שכוללים את הפרמטר המבוקש. זה יכול להיות ממוצע, כמו אצלנו, או פרמטר אחר דוגמת פרופורציה או שונות.

דגימות אקראיות שונות מאותה אוכלוסייה יתנו טווחים שונים של תוצאות מה שיגרום לרווח בר-סמך שונה עבור כל דגימה כאשר חלק יחסי מכל הרווחי בר סמך של הדגימות יכיל את הפרמטר באוכלוסיה. חלק יחסי זה נקבע על פי רמת הבטחון המוגדרת עבור הרווח בר-סמך. לדוגמה, המשמעות של רמת בטחון של 95% היא שאם ניקח 20 דגימות מהאוכלוסייה, נצפה ש-19 מתוכם יכילו בתוך הרווח בר-סמך שלהם את הפרמטר, ואחת לא תכיל.

מסקנה: הרווח בר-סמך מייצר טווחים שברמת בטחון רצויה מכיל את הפרמטר המבוקש.

דבר נוסף אליו צריך לשים לב הוא שבמרכז הרווח בר-סמך נמצא הפרמטר הנקודתי שמעניין אותנו, דוגמת הממוצע. שולי השגיאה סביב הפרמטר מהווים את הרווח בר-סמך. שוליים רחבים יותר מצביעים על מדגם שיש בו שונות רבה יותר מה שאומר שההערכה שלנו את הפרמטר היא פחות מדויקת. לדוגמה, אם בשני מדגמים קיבלנוו את הרווח בר-סמך של הממוצע שהוא: (157, 173) בראשון ו-(164, 166) בשני אז נוכל להעריך שהמדגם השני נותן הערכה מדויקת יותר של הממוצע.

איך לא ליפול בפח כשמשתמשים ברווח בר-סמך להסקה סטטיסטית

יצא לי לראות אנשים שמסתכלים על גרף התוצאות ומשווים את הרווח בר סמך בין שתי קבוצות כדי לקבוע האם ההבדל בין הקבוצות הוא משמעותי. אם הרווח בר סמך חופף אז הם מסיקים שאין הבדל משמעותי בין הממוצעים, ואם אין חפיפה, המסקנה היא שההבדל משמעותי.

זה נכון שאם הרווח בר סמך של שתי הקבוצות אינם חופפים אז ההפרש הוא משמעותי. אבל, ייתכן מצב של חפיפה ועדיין ההבדלים בין ממוצעי הקבוצות יהיו משמעותיים. להלן נתוני שתי דגימות של נשים שמדדנו את גובהם:

Sample1 = [1.58, 1.61, 1.56, 1.52, 1.44]

Sample2 = [1.67, 1.55, 1.63, 1.69, 1.72]

הרווח בר-סמך של הקבוצות חופפים כפי שאפשר ללמוד מחישוב הרווח בר-סמך עבור שתי הקבוצות:

Group 1: (1.46, 1.62)
Group 2: (1.57, 1.73)

וכפי שניתן ללמוד מהגרף הבא:

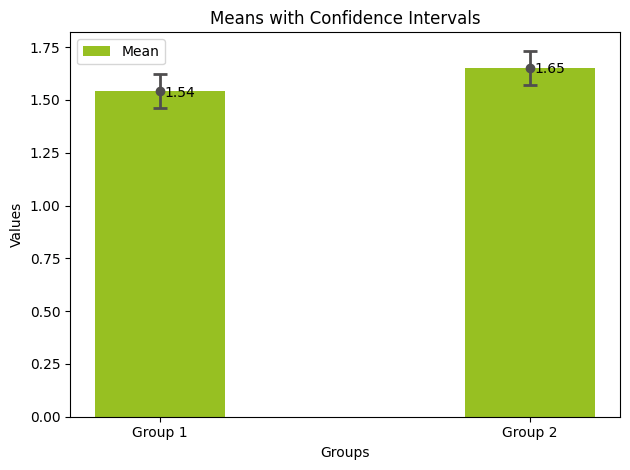
אבל בחינת הפרש הממוצעים תחת הנחת האפס שאין הבדל בין הקבוצות נותנת תוצאה משמעותית סטטיסטית p=0.029

מזה צריך ללמוד שלא כדאי למהר ולהסיק לגבי הבדלים משמעותיים בין קבוצות רק על סמך גרף. פתרון שתמיד עובד הוא להשתמש במבחן סטטיסטי דוגמת מבחן t לבחינת השערות.

את החלק הזה של המדריך ביססתי על קוד הפייתון הבא:

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import ttest_ind


def plot_bars_with_error_bars(data, labels):
   """Plots bar plots with error bars for the given data."""
   n_groups = len(data)
   index = np.arange(n_groups)
   bar_width = 0.35
   opacity = 1
   error_config = {'ecolor': '#504e4f', 'linewidth': 2}


   fig, ax = plt.subplots()
   rects1 = ax.bar(index, [np.mean(group) for group in data], bar_width,
                   alpha=opacity, color='#97c022', label='Mean')


   # Calculate confidence intervals for each group
   cis = [calculate_confidence_interval(group) for group in data]
   cis_lower = [ci[0] for ci in cis]
   cis_upper = [ci[1] for ci in cis]
   errors = [(cis_upper[i] - cis_lower[i]) / 2 for i in range(len(data))]


   ax.errorbar(index, [np.mean(group) for group in data], yerr=errors, fmt='o',
               elinewidth=2, capsize=5, capthick=2, barsabove=True, color='#504e4f')


   ax.set_xlabel('Groups')
   ax.set_ylabel('Values')
   ax.set_title('Means with Confidence Intervals')
   ax.set_xticks(index)
   ax.set_xticklabels(labels)
   ax.legend()


   # Add mean labels inside the bars
   for rect in rects1:
       height = rect.get_height()
       ax.annotate(f'{height:.2f}',
                   xy=(rect.get_x() + rect.get_width() / 2, height),
                   xytext=(3, 4),  # (horizontal, vertical) offsets
                   textcoords="offset points",
                   ha='left',  va='top')


   fig.tight_layout()
   plt.show()


def perform_t_test(data1, data2):
   """Performs a t-test to compare the means of two groups."""


   return ttest_ind(a=data1, b=data2, equal_var=False)


# Example usage
group1_data = [1.58, 1.61, 1.56, 1.52, 1.44]
group2_data = [1.67, 1.55, 1.63, 1.69, 1.72]


print("**There is an overlap in the confidence intervals for the mean of the groups:**")
ci1 = calculate_confidence_interval(group1_data)
ci2 = calculate_confidence_interval(group2_data)
print(f"Group 1: {ci1}")
print(f"Group 2: {ci2}")


print("**As you can see in the following plot:**")
plot_bars_with_error_bars([group1_data, group2_data], ["Group 1", "Group 2"])


print("**But when doing a t-test to compare the two groups means:**")
t_statistic, pvalue = perform_t_test(group1_data, group2_data)
print(f"p-value = {pvalue:.3f}")

לסיכום

סטטיסטיקה עוסקת בהערכה של פרמטרים באוכלוסייה דוגמת ממוצע או שונות. כאשר לרוב קשה ואף בלתי אפשרי למדוד את כלל האוכלוסיה, ולכן משתמשים בדגימות. התוצאות שמתקבלות הינם קירוב מוערך של הפרמטרים באוכלוסייה. בגלל שהפרמטר המחושב הוא רק הערכה אנחנו מעוניינים להגדיר טווח בתוכו עשוי להמצא בסבירות גבוהה הפרמטר. טווח שיאפשר לנו להגיד משהו כדוגמת, "על סמך תוצאות המחקר אנו יכולים להיות בטוחים שהממוצע באוכלוסיה נמצא בטווח הערכים שמצאנו בסבירות גבוהה". הטווח בתוכו אנו מעריכים שנמצא הפרמטר נקרא רווח בר-סמך (confidence interval או בקיצור CI). אותו הסברנו במדריך.

אולי גם זה יעניין אותך?

סטיית תקן ושגיאת תקן

מבחן t-test לבחינת השערות

מבחן ANOVA - האם ממוצעי קבוצות שונים סטטיסטית

לכל המדריכים בנושא של למידת מכונה

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים