מציאת ערכים ווקטורים טיפוסיים של מטריצה עם ובלי פייתון

וקטורים וערכים טיפוסיים מאפשרים לנו לאפיין מטריצות ולצמצם נתונים מורכבים למרכיבים חיוניים מה שעוזר בניתוח של מערכות נתונים מורכבות. במדריך זה נראה כיצד לחשב אותם בלי להשתמש בקוד עבור מערכת פשוטה וכיצד להשתמש בספריית Numpy של פייתון לפתרון מטריצות בכל רמה של מורכבות.

מציאת וקטורים וערכים טיפוסיים ללא קוד

נמצא את הערכים הטיפוסיים והוקטורים הטיפוסיים (eigenvalues and eigenvectors) של מטריצה שממדיה 2 X 2:

$$ A = \begin{bmatrix} 1 & 0.5 \\ 0.5 & 1 \end{bmatrix} $$

לוקטור ריבועי ייתכן וקיים צמד של וקטור וסקלר אשר מקיימים:

$$ A v = \lambda v $$

נסדר מחדש:

$$ A v - \lambda v = 0 $$

כיוון שכפל ב-I, מטריצת הזהות, כמוהו ככפל ב-1, אנו יכולים לעשות את הדבר הבא שיעזור לנו בפיתוח המשוואה האופיינית:

$$ A v - \lambda I v = 0 $$

נוציא את הוקטור v מחוץ לסוגריים:

$$ (A - \lambda I) v = 0 $$

בשלב זה, יש לנו שתי אפשרויות או שהוקטור שווה ל-0:

$$ v = 0 $$

או שהמטריצה שווה ל-0:

$$ (A - \lambda I) = 0 $$

אבל הוקטור חייב להיות שונה מ-0 (v ≠ 0) כיוון שאנחנו לא מעוניינים בפתרונות טריוויאליים.

אם המטריצה הייתה הופכית אז ניתן היה לכפול את שני האגפים בהופכי:

$$ (A - \lambda I)^{-1} (A - \lambda I) v = (A - \lambda I)^{-1} 0 $$

כדי לקבל:

$$ I v = 0 $$

כיוון שכפל במטריצת הזהות לא משנה את המטריצה, נקבל ש:

$$ v = 0 $$

קיבלנו סתירה כיוון שהוקטור v לא יכול להיות גם שווה ל-0 וגם שונה ממנו. מה שאומר שלמטריצה לא יכול להיות הופכי.

אם למטריצה אין הופכי אז הדטרמיננטה שלה בהגדרה שווה ל-0:

$$ det(A - \lambda I) = 0 $$

נציב את המטריצה שלנו כדי לקבל את הפולינום הטיפוסי:

$$ det( \begin{bmatrix} 1 & 0.5 \\ 0.5 & 1 \end{bmatrix} - \lambda \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}) = 0 $$

$$ det( \begin{bmatrix} 1 & 0.5 \\ 0.5 & 1 \end{bmatrix} - \begin{bmatrix} \lambda & 0 \\ 0 & \lambda \end{bmatrix}) = 0 $$

$$ det( \begin{bmatrix} 1-\lambda & 0.5 \\ 0.5 & 1-\lambda \end{bmatrix} ) = 0 $$

נשתמש באלגוריתם לפתרון דטרמיננטה של 2X2 כדי להפיק משוואה טיפוסית:

$$ \lambda^2 - 2\lambda + 0.75 = 0 $$

נפתור את המשוואה כדי לקבל את הערכים הטיפוסיים:

$$ \lambda_{1,2} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

$$ \lambda_{1,2} = \frac{2 \pm \sqrt{4 - 3}}{2} $$

הצבה ופתרון המשוואה נותנת את הערכים הטיפוסיים:

$$ \lambda_1 = 1.5 \\ \lambda_2 = 0.5 $$

את הווקטורים הטיפוסיים נמצא על ידי הצבת ערכי הערכים הטיפוסיים חזרה לתוך המשוואה הטיפוסית:

$$ (A - \lambda I) v = 0 $$

$$ E_{1.5} = \begin{bmatrix} 1-1.5 & 0.5 \\ 0.5 & 1-1.5 \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$

כיוון ששתי השורות נותנות את אותה התוצאה אפשר להשתמש רק באחת מהם בשביל הפתרון. נבחר בעליונה.

נכפול את המטריצות, ונסדר את התוצאה:

$$ x_{1} = x_{2} $$

מה שאומר שהוקטור הטיפוסי הוא משפחה של פתרונות שבו האיברים הראשון והשני שווים. כך נציין את זה:

$$ E_{1.5} = span( \begin{bmatrix} 1 \\ 1 \end{bmatrix} ) $$

נמצא את הוקטור האופייני השני באותו האופן, ונקבל:

$$ E_{0.5} = span( \begin{bmatrix} 1 \\ -1 \end{bmatrix} ) $$

נבדוק את התוצאה של הראשון האם מתקיים השיוויון:

$$ A v = \lambda v $$

$$ \begin{bmatrix} 1 & 0.5 \\ 0.5 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \end{bmatrix} = 1.5 \begin{bmatrix} 1 \\ 1 \end{bmatrix} $$

והשיוויון אכן מתקיים.

את אותה הבדיקה אפשר לעשות כדי לוודא את הקומבינציה של הערך והוקטור הטיפוסי האחרים שקיבלנו.

שימוש בפייתון למציאת ערכים ווקטורים טיפוסיים של מטריצה

אפשר להשתמש בפייתון למציאת ערכים ווקטורים טיפוסיים של מטריציה. אפשרות מועילה ביותר ביישומים אמיתיים בהם המכונה צריכה לפתור מטריצות מורכבות כדי לספק תשובה.

לצורך הפתרון נשתמש בספריית Numpy:

import numpy as np

# Matrix formatted as a Numpy array of arrays
A = np.array([[1, 0.5], [0.5, 1]])

# This is where the magic happens
lamdas, V = np.linalg.eig(A)

# Print the typical values
print(lamdas)

# Print the typical vectors
print(V)

הערכים הטיפוסיים המחושבים הם:

[1.5 0.5]

הוקטורים הטיפוסיים המחושבים הם:

[[0.70710678 0.70710678]
 [-0.70710678 0.70710678]]

• העמודה הראשונה היא משפחת הפתרונות עבור הערך הטיפוסי λ = 1.5 כאשר כל הוקטורים במשפחה מקיימים שויון בין הערך הראשון והשני, משמע:

  $$ E = span( \begin{bmatrix} 1 \\ 1 \end{bmatrix} ) $$

• העמודה השנייה היא משפחת הפתרונות עבור הערך הטיפוסי λ = 0.5 כאשר כל הווקטורים במשפחה מקיימים שהערך השני הוא השלילי של הראשון:

  $$ E = span( \begin{bmatrix} 1 \\ -1 \end{bmatrix} ) $$

נוודא:

# Let's confirm
# Eigenvectors
v = V[:, 0]

# Eigenvalues
lamda = lamdas[0]

np.dot(A, v) == lamda * v
# print(np.dot(A, v))
# print(lamda * v)

התוצאה:

array([ True,  True])

• השיוויון אכן מתקיים.

קוד להצגת הטרנספורמציות כולל האייגנים

קוד הפייתון הבא שימש אותי להצגת הלפני ואחרי של הטרנספורמציה כולל גודל וכיוון האייגנוקטורים:

import numpy as np
import matplotlib.pyplot as plt
from numpy.linalg import eig

# Define the coordinates
coords_before = [[1, 0], [0, 1]]
coords_after = [[1,0.5],[0.5,1]]
coords_list = [coords_before, coords_after]

grid_size = 100

def generate_dot_grid_coordinates(grid_size, spacing=6):
    """Generate coordinates for a grid of dots in a given size with specified spacing with the center at [0,0].
       Also generates a gradient based on the distance from the center."""

    # Calculate half the grid size
    half_size = grid_size // 2

    # Create x and y ranges
    x = np.arange(-half_size, half_size + spacing, spacing)
    y = np.arange(-half_size, half_size + spacing, spacing)

    # Generate grid coordinate matrices
    xv, yv = np.meshgrid(x, y)

    # Flatten and stack the coordinates
    coords = np.vstack([xv.ravel(), yv.ravel()])

    # Create the gradient based on the x and y coordinates
    gradient_x = (coords[0] - np.min(coords[0])) / (np.max(coords[0]) - np.min(coords[0]))
    gradient_y = (coords[1] - np.min(coords[1])) / (np.max(coords[1]) - np.min(coords[1]))

    # Combine the gradients
    gradient = (gradient_x + gradient_y) / 2

    return coords, gradient

def plot_vectors(vectors, colors):
    plt.axvline(x=0, color='lightgray')
    plt.axhline(y=0, color='lightgray')

    for i in range(len(vectors)):
        x = np.concatenate([[0, 0], vectors[i]])
        plt.quiver([x[0]], [x[1]], [x[2]], [x[3]],
                   angles='xy', scale_units='xy', scale=1, color=colors[i])

# Generate grid coordinates and gradient
coords, gradient = generate_dot_grid_coordinates(grid_size)

# Loop through the coordinates and plot eigenvectors
for i, coord in enumerate(coords_list):
    # Transform the grid coordinates using the transition matrix `coord`
    transformed_coords = np.dot(coord, coords)

    # Calculate the limits for the plot
    x_min, x_max = np.min(transformed_coords[0]) - 5, np.max(transformed_coords[0]) + 5
    y_min, y_max = np.min(transformed_coords[1]) - 5, np.max(transformed_coords[1]) + 5

    # Create the plot
    plt.figure()

    # Plot the transformed grid as background
    plt.scatter(transformed_coords[0], transformed_coords[1], c=gradient, cmap='ocean', s=10, alpha=0.6)

    # Calculate eigenvalues and eigenvectors
    eigenvalues, eigenvectors = eig(coord)

    # Plot eigenvectors
    scale_factor = grid_size / 2
    eigenvector = eigenvectors[:, 0]
    magnitude = np.sqrt(np.abs(eigenvalues[0]))
    red_vector = [scale_factor * magnitude * eigenvector[0], scale_factor * magnitude * eigenvector[1]]

    eigenvector = eigenvectors[:, 1]
    magnitude = np.sqrt(np.abs(eigenvalues[1]))
    blue_vector = [scale_factor * magnitude * eigenvector[0], scale_factor * magnitude * eigenvector[1]]

    plot_vectors([red_vector, blue_vector], ["red", "blue"])

    # Print eigenvalues and eigenvectors
    print(f"λ1 = {np.round(eigenvalues[0], 2)}")
    print(f"λ2 = {np.round(eigenvalues[1], 2)}")
    print(f"det(A) = {np.linalg.det(coord)}")
    print(eigenvectors[:, 0])
    print(eigenvectors[:, 1])

    # Set plot limits dynamically
    plt.xlim(x_min, x_max)
    plt.ylim(y_min, y_max)
    plt.show()

התוצאה:

* הקוד עובד כל עוד התוצאה היא מספרים אמיתיים.

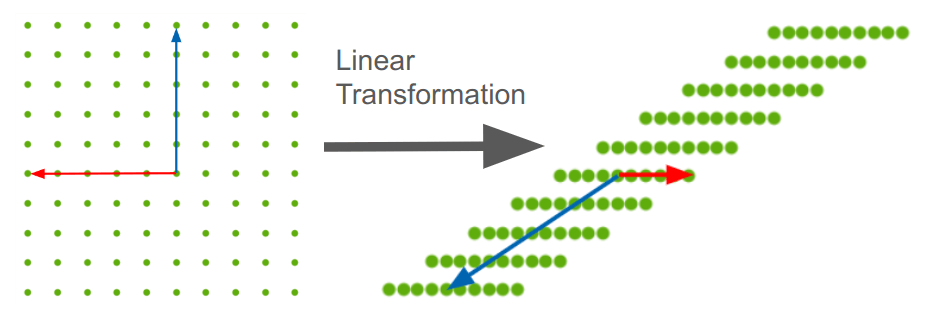
• אפשר לראות שהטנספורמציה מאריכה את הוקטור הטיפוסי האדום בשיעור של פי-1.5 ומכווצת את הוקטור הטיפוסי הכחול פי 0.75. סה"כ הטרנספורמציה מכווצת את השטח ל-75% מהמקור כפי שאפשר ללמוד מחישוב הדטרמיננטה: det(A) = 0.75 .

למדריכים נוספים בסדרה על למידת מכונה

12 דברים שאתה חייב לדעת כשאתה עובד עם ספריית Numpy של Python

למידת מכונה בלתי מפוקחת באמצעות PCA

מציאת יחס הזהב בתוך סדרת מספרים עולה באמצעות (קצת) אלגברה לינארית

לכל המדריכים בנושא של למידת מכונה

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים