מציאת יחס הזהב בתוך סדרת מספרים עולה באמצעות (קצת) אלגברה לינארית

סדרת פיבונאצ'י מורכבת ממספרים כאשר כל מספר הוא סכום השניים הקודמים: 0, 1, 1, 2, 3, 5, 8, 13 וכיו"ב.

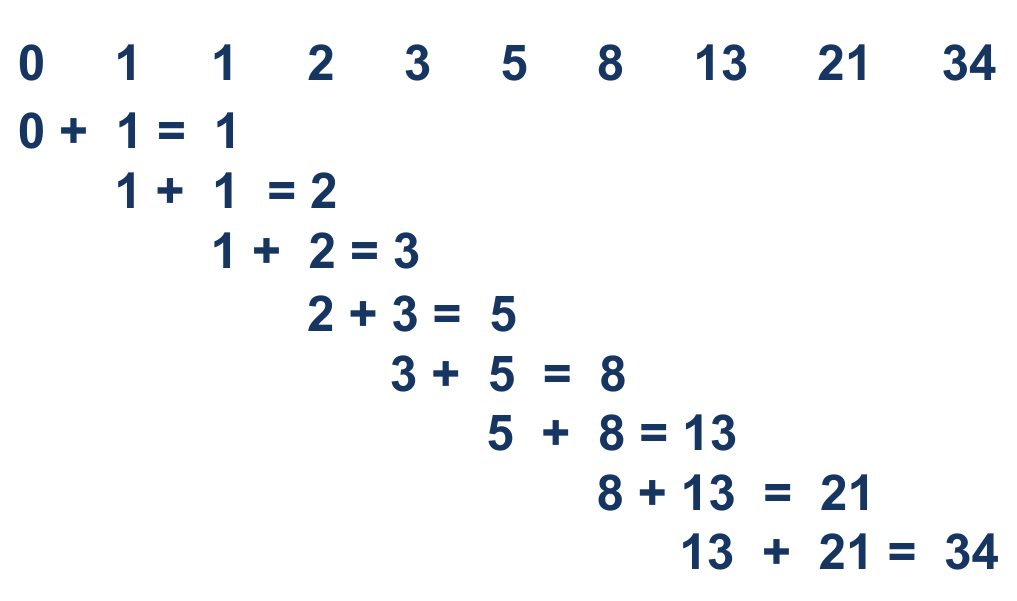
את סדרת פיבונאצ'י ניתן לבטא באמצעות מטריצה וערכי הוקטורים העצמיים שלה eigenvalues ו-eigenvectors כיוון שהם מאפשרים להבין את הדינמיקה ארוכת הטווח של מערכות, ולחשב את שיעור הגדילה אליו תתכנס המערכת בסופו של דבר.

בהינתן מטריצה A, יכולים להיות לה ווקטורים עצמיים, כאשר כל אחד משויך לערך עצמי ספציפי (λ). הערך העצמי פועל כמקדם מתיחה. כאשר מכפילים וקטור שונה מאפס מסוים (ווקטור עצמי) במטריצה, כיוון הווקטור לא משתנה אלא הוא נמתח או מתכווץ בהתאם לגודל הערך העצמי. המשוואה הבאה מציגה את הקשר בין הערכים העצמיים לוקטורים העצמיים:

A * v = λ * v

כאשר A היא המטריצה, v הוא הווקטור העצמי ו-λ הוא הערך העצמי.

המשוואה הבאה מבטאת את החוקיות של סדרת פיבונאצ'י:

$$ F_{n} = 1 \cdot F_{n-1} + 1 \cdot F_{n-2} $$

• סכום שני איברים עוקבים בסדרת פיבונאצ'י שווה לאיבר הבא בסדרה.

נוסיף משוואה טריוויאלית כדי למצוא מטריצה ריבועית שתבטא את היחסים בין המספרים העוקבים בסדרה:

$$ F_{n-1} = 1 \cdot F_{n-1} + 0 \cdot F_{n-2} $$

ניצור משתי המשוואות מערכת של שתי משוואות:

$$ F_{n} = 1 \cdot F_{n-1} + 1 \cdot F_{n-2} \\ F_{n-1} = 1 \cdot F_{n-1} + 0 \cdot F_{n-2} $$

• המשוואה הראשונה אומרת שאם מחברים את שתי הספרות הקודמות בסדרה מקבלים את הספרה הנוכחית.
• המשוואה השנייה היא מקרה טריוויאלי שאנחנו צריכים כדי להשלים מטריצה ריבועית.

את הטרנספורמציה שעושה מערכת המשוואות ניתן לכתוב כמטריצה ריבועית:

$$A = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}$$

המטריצה היא מטריצת פיבונאצ'י שאם נכפול בה כל וקטור של 2 מספרים עוקבים בסדרת פיבונאצ'י נקבל את האיבר הבא בתור:

$$A = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}$$

נוודא שמטריצת פיבונאצ'י עובדת.

נתון וקטור שמכיל את שני המספרים העוקבים הראשונים בסדרת פיבונאצ'י:

$$\nu _{0} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}$$

נכפול את מטריצת פיבונאצ'י בוקטור ונקבל את הוקטור המייצג את האיברים השני והשלישי:

$$\nu _{1} = A \nu _{0} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \end{bmatrix}$$

נכפול את מטריצת פיבונאצ'י בוקטור המייצג את האיברים השני והשלישי ונקבל את הוקטור המייצג את האיברים השלישי והרביעי:

$$\nu _{2} = A \nu _{1} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 2 \\ 1 \end{bmatrix}$$

נכפול את מטריצת פיבונאצ'י בוקטור המייצג את האיברים השלישי והרביעי ונקבל את הוקטור המייצג את האיברים הרביעי והחמישי:

$$\nu _{3} = A \nu _{2} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 2 \\ 1 \end{bmatrix} = \begin{bmatrix} 3 \\ 2 \end{bmatrix}$$

כאשר המקרה הכללי הוא:

$$ \begin{bmatrix} F _{n}\\ F _{n-1} \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} F _{n-1}\\ F _{n-2} \end{bmatrix} $$

נפתור את המקרה הכללי ונקבל חזרה את מערכת המשוואות:

$$ F_{n} = F_{n-1} + F_{n-2} \\ F_{n-1} = F_{n-1} $$

ה-eigenvector, הוקטור הטיפוסי ν של מטריצה A הוא וקטור שערכו אינו אפס אשר מקיים את המשוואה A ν = λ ν כאשר λ הוא סקלאר eigenvalue.

ניתן לסדר מחדש את המשוואה (A - λI)ν = 0 ולקבל:

$$ A \nu = \lambda \nu \\ A \nu - \lambda \nu = 0 \\ (A - \lambda) \nu = 0 $$

נכפיל את λ במטריצת הזהות I שזה באלגברה לינארית כמו לכפול ב-1 דבר שיקל עלינו לפתח את המשוואה:

$$ (A - \lambda I) \nu = 0 $$

כיוון שאנו מעוניינים במקרה הלא טריוויאלי בו ν ≠ 0 המטריצה A - λI יכולה להיות שווה ל-0 מה שאומר שאין לו הופכי והוא סינגולרי.

בגלל ש A - λI אין לו הופכי הדטרמיננטה שלו שווה בהכרח לאפס:

$$ det(A - \lambda I) = 0 $$

נפתח את הביטוי:

$$ \text{det}\left( \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} - \lambda \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \right) = 0 $$

$$ {det}\left( \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} - \begin{bmatrix} \lambda & 0 \\ 0 & \lambda \end{bmatrix} \right) = 0 $$

$$ {det}\left( \begin{bmatrix} 1 - \lambda & 1 \\ 1 & -\lambda \end{bmatrix} \right) = 0 $$

המשוואה שפיתחנו היא המשוואה האופיינית.

נרחיב את הדטרמיננטה עבור מטריצה של 2X2:

$$ (1 - \lambda)(-\lambda) - (1)*(1) = 0 $$

נפשט:

$$ \lambda^2 - \lambda - 1 = 0 $$

נפתור את המשוואה הריבועית לצורך מציאת הערכים הטיפוסיים:

$$ \lambda = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

$$ a = 1, b = -1, c = -1 $$

$$ \lambda = \frac{1 \pm \sqrt{(-1)^2 - 4(1)(-1)}}{2(1)} $$

$$ \lambda_1 = \frac{1 + \sqrt{1 + 4}}{2} = \frac{1 + \sqrt{5}}{2} \approx 1.618 $$

$$ \lambda_2 = \frac{1 - \sqrt{1 + 4}}{2} = \frac{1 - \sqrt{5}}{2} \approx -0.618 $$

מצאנו שני ערכים טיפוסיים. האם הם נכונים?

ידוע שהעִקְבָה (trace) של מטריצה ריבועית היא סכום האיברים באלכסון הראשי של המטריצה.

ידועה לנו מטריצת פיבונאצ'י:

$$A = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}$$

שבה סכום האיברים באלכסון הוא 1, וזה גם הסכום של שני הערכים הטיפוסיים, ולפיכך הערכים הטיפוסיים אותם מצאנו נראים נכונים.

הערך הטיפוסי אותו מצאנו 1.618 הוא מספר לא רציונלי הידוע בשמו היווני פיי (בניגוד לפאי π מבטאים בפ רפויה) והוא מסומל באות היוונית φ:

$$ \phi \approx 1.6180339887 $$

מספר זה ידוע בתור יחס הזהב והוא מופיע במספר רב של תופעות מתמטיות וטבעיות. יחס הזהב מתקיים כאשר היחס בין שתי כמויות זהה ליחס בין סכומם לבין הגדולה מבין הכמויות.

בהינתן:

$$ a > b > 0 $$

יחס הזהב הוא:

$$ \phi = \frac{a + b}{a} = \frac{a}{b} = \frac{1 + \sqrt{5}}{2} \approx 1.618 $$

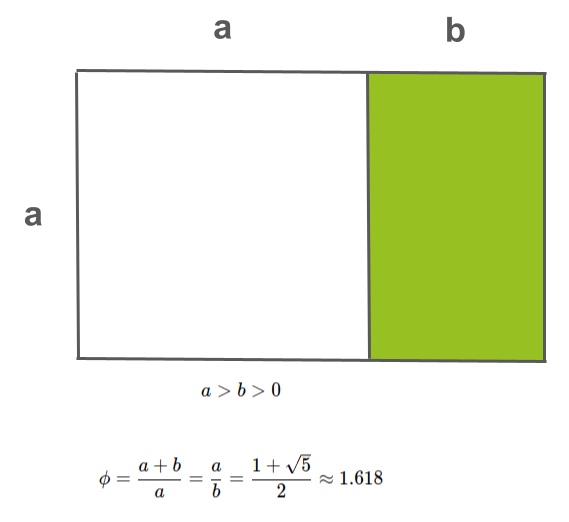
יחס הזהב מופיע בגיאומטריה כאשר היחס בין אלכסון לצלע במחומש משוכלל שווה ל-φ. בנוסף, משולש שהיחס בין צלעו לבסיסו הוא φ נקרא משולש הזהב.

בכל הנוגע לסדרת מספרי פיבונאצ'י היחס בין הספרות הסמוכות בסדרה הולך ומתכנס ליחס הזהב ככל שהרצף מתקדם. לדוגמה:

$$ \frac{2}{1} = 2 $$

$$ \frac{3}{2} = 1.5 $$

$$ \frac{5}{3} = 1.6667 $$

$$ \frac{8}{5} = 1.6 $$

$$ ... $$

$$ \frac{21}{13} = 1.615 $$

$$ ... $$

$$ \frac{610}{377} = 1.618 $$

בעולם הטבע, ישנם דוגמאות רבות לסדרות פיבונאצ'י. לדוגמה, סידור העלים סביב גבעולים מציית לסדרת פיבונאצ'י כיוון שיחס זה הינו האופטימלי מבחינת החשיפה לשמש, לגשם ולאוויר. הסידור הלולייני של הגרעינים בפרחי החמנית מציית אף הוא לכללי הסדרה. גם קונכיית הנאוטילוס הימי כמו פרח החמנייה מהווה דוגמה ללוליין לוגריתמי בו כל עלייה בגודל הקונכייה גורמת לעלייה פרופורציונית ברדיוס, בשיעור המציית ליחס הזהב. מערבולות ים, הוריקנים וגלקסיות חלזוניות דוגמת שביל החלב בה אנו חיים הינם דוגמאות נוספות ללוליינים לוגריתמיים בעולם הטבע בהם הדינמיקה של המערכת ועקרון הדמיון העצמי מתכנסים לפתרון המדגים את יחס הזהב.

את חיתוך הזהב ניתן למצוא באמנות. לדוגמה, יש הטוענים שלאונרדו דה וינצ'י השתמש בחיתוך הזהב ביוצרו את המונה ליזה ייתכן שבגלל שהיו אומנים אחרים שחיו בתקופת הרנסנס וסברו שיש משהו אלוהי במספר φ. האדריכל לה קורבוזייה גם כן השתמש בחיתוך הזהב כדי להעניק פרופורציה הרמונית למבנים האייקונים את בנייתם תכנן במאה ה-20, כאשר היצירה שלו האדם המודולורי עושה שימוש מרהיב ביחס הזהב (נא לחפש תמונות בגוגל של The Modulor Man).

כיצד למצוא את האיבר במיקום ה-nי של סדרת פיבונאצ'י באמצעות (קצת) אלגברה לינארית

אחרי שראינו את הקשר בין הערך הטיפוסי φ=1.618 לבין היחסים ארוכי הטווח בין איברים עוקבים בסדרת פיבונאצ'י מעניין יהיה לגלות כיצד להשתמש בידע הזה כדי לחשב את האיבר ה-nי בסדרת פיבונאצ'י. את התשובה מצאתי במאמר מעולה שאני ממליץ בחום לקרוא אותו The Linear Algebra View of the Fibonacci Sequence/ Andrew Chamberlain. במדריך זה רק אסכם את דברי ההסבר המופיעים במאמר לעיל, ואציג את המודל הלינארי לחישוב האיבר ה-nי של סדרת פיבונאצ'י אותו פיתח כותב המאמר.

המאמר הציג שיטה לחישוב ערכים בסדרת פיבונאצ'י באמצעות מודלים לינארים דינאמיים (DLMs). השיטה מבוססת על דיאגונליזציה של מטריצת פיבונאצ'י וחישוב ערכים בטווח הארוך של מערכות דינמיות.

מודלים לינארים דינאמיים (DLMs) הם כלי סטטיסטי רב עוצמה וגמיש המשמש לניתוח נתוני סדרות זמן שבהם הנתונים מציגים תלות מסוימת בערכים הקודמים שלהם. במילים פשוטות יותר, DLMs מאפשרים לך להבין כיצד מערכת משתנה לאורך זמן על ידי התחשבות לא רק במצב הנוכחי, אלא גם בהיסטוריה שלה.

הצורה הכללית למודלים לינארים דינאמיים דוגמת:

$$ F_{n} = F_{n-1} + F_{n-2} \\ F_{n-1} = F_{n-1} $$

בהם כפל חוזר ונשנה במטריצה מקדם את הסידרה כולה היא:

$$ A \nu_{0} = \nu_{1} $$

• ν_0 הינו המצב לפני הטרנספורמציה, A היא מטריצת הטרסנפורמציה, ו- ν_1 היא מצב המערכת בעקבות הטרנספורמציה.

אנחנו יכולים להשתמש בערכים ובווקטורים הטיפוסיים על מנת לחשב את הערכים בטווח הארוך של מערכות דינמיות.

לשם כך נעזר בזהות הבאה:

$$ A S = S \Lambda $$

• S היא מטריצה שעמודותיה הן הווקטורים העצמיים של A.

• Λ היא מטריצה אלכסונית (=דיאגונלית) בה כל איבר אלכסוני הוא הערך העצמי המתאים לעמודות הווקטור העצמי.

הזהות AS = SΛ עושה דיאגונליזציה של מטריצה A לרכיבי הוקטורים והערכים הטיפוסיים. מטרת הדיאגונליזציה היא לפשט את החישובים, כפי שנראה בהמשך.

נגדיר את המטריצות S ו- Λ שתיהם מטריצות ריבועיות בעלות ממדים של 2X2:

1. מטריצה S בה העמודות הם שני הוקטורים הטיפוסיים של מטריצת הטרנספורמציה A.

2. מטריצה אלכסונית (=דיאגונלית) Λ בה האלכסון יכיל את הערכים הטיפוסיים של מטריצת הטרנספורמציה, ויתר התאים יקבלו ערך 0.

נחלץ את המטריצה A מתוך הזהות על ידי הכפלת שני אגפי המשוואה בהופכי של S:

$$ A S = S \Lambda \\ A = S \Lambda S^{-1} $$

נציב את הערך של A לתוך המודל הלינארי:

$$ A = S \Lambda S^{-1} \\ \nu_{1} = A \nu_{0} \\ \nu_{1} = S \Lambda S^{-1} \nu_{0} $$

באמצעות המשוואה הדינאמית בכל פעם שנכפול במטריצת פיבונאצ'י A נתקדם לאיבר הבא של הסידרה . אז במידה ורוצים לחשב את האיבר במיקום k כל מה שצריך הוא להעלות את המטריצה האלכסונית Λ בחזקת k. בהתאם, המשוואה הבאה משמשת למציאת האיבר במקום k של הסדרה:

$$ \nu_{k} = S \Lambda^{k} S^{-1} \nu_{0} $$

• זה המודל הליניארי שלנו בצורה פשוטה לחישוב.

בשביל למצוא את המטריצות S ו- Λ אנחנו צריכים למצוא את הערכים והווקטורים הטיפוסיים.

את הערכים הטיפוסיים כבר חישבנו:

$$ \lambda_1 = \frac{1 + \sqrt{1 + 4}}{2} = \frac{1 + \sqrt{5}}{2} \approx 1.618 $$

$$ \lambda_2 = \frac{1 - \sqrt{1 + 4}}{2} = \frac{1 - \sqrt{5}}{2} \approx -0.618 $$

נתבסס על הערכים הטיפוסיים לצורך חישוב הווקטורים הטיפוסיים.

וקטור עצמי x של מטריצה A הוא וקטור שונה מאפס המקיים את המשוואה:

$$ A \mathbf{x} = \lambda \mathbf{x} $$

ניתן לסדר מחדש את משוואת הווקטור העצמי על ידי חיסור λx משני צידי המשוואה, וכפילה ב-I שהינו מטריקס זהות, ולקבל:

$$ (A - \lambda I) \mathbf{x} = \mathbf{0} $$

כאשר:

• A המטריצה הריבועית שעבורה אנו מחפשים את הווקטורים העצמיים.
• λ הערך העצמי שאותו אנו בוחנים.
• I מטריצת היחידה.
• x הווקטור העצמי המתאים שאותו אנו מחפשים. כאשר למעשה אנו מעוניינים בוקטור עמודה המכיל 2 איברים.

פיתרון המשוואה `(A−λI)x = 0` לעיל יאפשר את מציאת הווקטור העצמי המשויך לערך העצמי λ. כאשר פיתרון המערכת חייב להיות לא טריוויאלי (הוקטורים שונים מ-0).

נפתור את המערכת עבור λ = φ:

$$ (A - \lambda I) \mathbf{x} = \mathbf{0}\\ \begin{bmatrix} 1 - (\frac{1 + \sqrt{5}}{2}) & 1 \\ 1 & - (\frac{1 + \sqrt{5}}{2}) \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = \mathbf{0} $$

נפשט:

$$ \frac{1 - \sqrt{5}}{2} x_{1} + x_{2} = \mathbf{0} $$

כיוון ש-x2 הוא האיבר החופשי הכי קל להציב במקומו 1, דבר שיאפשר לנו לחלץ את x1, ואחרי שנחלץ את x1 אנחנו יכולים למצוא את הערכים הקונקרטיים של הוקטור הטיפוסי הראשון של מטריצת פיבונאצ'י:

$$ V_{1} = \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = \begin{bmatrix} \frac{1 + \sqrt{5}}{2} \\ 1 \end{bmatrix} $$

חישוב דומה ימצא את הוקטור הטיפוסי השני:

$$ V_{2} = \begin{bmatrix} \frac{1 - \sqrt{5}}{2} \\ 1 \end{bmatrix} $$

חישבנו את הוקטורים העצמיים ν₁, ν₂ אבל האם אנחנו צודקים? הצפי הוא שהוקטורים העצמיים יהיו אורתוגנלים זה לזה היות ומטריצת פיבונאצ'י היא סימטרית, ואכן הם מאונכים זה לזה.

נרכיב את המטריצות S ו- Λ על בסיס הערכים והווקטורים העצמיים אותם חישבנו לעיל:

$$ S = \begin{bmatrix} \frac{1 + \sqrt{5}}{2} & \frac{1 - \sqrt{5}}{2} \\ 1 & 1 \end{bmatrix} $$

$$ \Lambda = \begin{bmatrix} \frac{1 + \sqrt{5}}{2} & 0 \\ 0 & \frac{1 - \sqrt{5}}{2} \end{bmatrix} $$

נשתמש בנוסחת הטרנספוזיציה לחישוב ההופכי של המטריצה S:

$$ S^{-1} = \begin{bmatrix} \frac{1}{\sqrt{5}} & \frac{\sqrt{5} - 1}{2 \sqrt{5}} \\ \frac{-1}{\sqrt{5}} & \frac{\sqrt{5} + 1}{2 \sqrt{5}} \end{bmatrix} $$

השלב האחרון כולל ביטוי של וקטור המצב הראשוני ν₀ כצירוף ליניארי של העמודות של S. ההצדקה מאחורי שלב זה נעוצה בתובנה שהוא מספק לגבי כמה כל וקטור עמודה ב-S תורם ליצירת האיבר הראשון בסדרה.

במונחים מתמטיים, אנו מייצגים את וקטור המצב הראשוני ν₀ כמכפלה של המטריצה S ושל וקטור c:

$$ \nu_{0} = S_{c} $$

כאן, c הוא וקטור עמודה המכיל מקדמים שקובעים את התרומה של כל וקטור עצמי ב-S ליצירת וקטור המצב הראשוני ν₀. הבנת צירוף זה היא קריטית מכיוון שהיא מאפשרת לנו להבחין בהשפעה של כל וקטור עצמי על הרכב האיבר הראשון בסדרה.

במונחים פרקטיים, פתרון עבור c מסייע לחשוף את המשקולות הספציפיות המוקצות לכל וקטור עצמי ב-S בעת בניית וקטור המצב הראשוני. ידע זה חיוני להבנת תפקידו של כל וקטור עצמי בעיצוב תנאי ההתחלה של סדרת פיבונאצ'י.

נחלץ את c מהמשוואה:

$$ c = S^{-1} \nu_{0} $$

את ν₀ המצב ההתחלתי של המערכת נגדיר עם האיברים השני והשלישי של סדרת פיבונאצ'י כי הכי נוח להתחיל את החישוב מהם:

$$ \nu_{0} = \begin{bmatrix} 1 \\ 1 \end{bmatrix} $$

• את המצב ההתחלתי אנחנו יכולים להגדיר על כל שני איברים עוקבים במערכת. הבחירה באיברים השני והשלישי היא מטעמי נוחות.

נחשב את c:

$$ c = \begin{bmatrix} \frac{1}{\sqrt{5}} & \frac{\sqrt{5} - 1}{2 \sqrt{5}} \\ \frac{-1}{\sqrt{5}} & \frac{\sqrt{5} + 1}{2 \sqrt{5}} \end{bmatrix} \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{5 + \sqrt{5}}{10} \\ \frac{5 - \sqrt{5}}{10} \end{bmatrix} $$

נציב את c המחושב לתוך המערכת הלינארית הדינמית:

$$ \nu_{k} = S \Lambda^{k} S^{-1} \nu_{0} \nu_{k} = S \Lambda^{k} c $$

ונקבל מערכת שלתוכה נוכל להציב כל k כדי לקבל את האיברים במיקום ה-k+2 וה-k+3:

$$ \begin{bmatrix} F_{k+3} \\ F_{k+2} \end{bmatrix} = \begin{bmatrix} \frac{1 + \sqrt{5}}{2} \\ 1 \end{bmatrix} (\frac{1 + \sqrt{5}}{2})^k \frac{5 + \sqrt{5}}{10} + \begin{bmatrix} \frac{1 - \sqrt{5}}{2} \\ 1 \end{bmatrix} (\frac{1 - \sqrt{5}}{2})^k \frac{5 - \sqrt{5}}{10} $$

• ניתן להציב לתוך הביטוי הזה כל k כדי לקבל את ערך האיברים k+2, k+3 בסידרת פיבונאצ'י. לדוגמה, מציבים k=97 כדי לקבל את ערך האיברים 99 ו-100.

קוד פייתון למציאת האיבר במיקום ה-k של סדרת פיבונאצ'י

קוד הפייתון הבא יחשב את ערך האיבר בסדרת פיבונאצ'י במיקום k של הסדרה תוך הסתמכות על מערכת המשוואות הלינאריות לעיל:

import numpy as np

def fibonacci_k_plus_two_and_three(k):
  """
  Calculates the (k+2)nd and (k+3)rd Fibonacci numbers using the given formula.

  Args:
    k: The integer index k.

  Returns:
    A numpy array containing the (k+2)nd and (k+3)rd Fibonacci numbers.
  """
  phi = (1 + np.sqrt(5)) / 2
  psi = (1 - np.sqrt(5)) / 2
  c1 = (5 + np.sqrt(5)) / 10
  c2 = (5 - np.sqrt(5)) / 10

  F_k_plus_three = phi**(k+1) * c1 + psi**(k+1) * c2
  F_k_plus_two   = phi**k * c1 + psi**k * c2

  return np.array([F_k_plus_two, F_k_plus_three])

# Example usage
k = 97
F_k_plus_two, F_k_plus_three = fibonacci_k_plus_two_and_three(k)
print(f"The {k+2}th Fibonacci number is: {F_k_plus_two}") 
print(f"The {k+3}th Fibonacci number is: {F_k_plus_three}")

תוצאת החישוב:

The 99th Fibonacci number is: 1.3530185234470717e+20
The 100th Fibonacci number is: 2.189229958345559e+20

הערכת השיטה החישובית למציאת איברי סדרת פיבונאצ'י

מה שמעניין הוא שככל ש-k גדל כך האיבר השני בביטוי שואף ל-0

$$ (\frac{1 - \sqrt{5}}{2})^k $$

מכיוון שהחלק הדומיננטי בביטוי הוא מה שעולה בחזקה וערך זה מתקרב ל-0 ככל שערך החזקה גדול יותר.

גם בחלקו הראשון של הביטוי החלק הדומיננטי הוא האיבר בחזקה:

$$ (\frac{1 + \sqrt{5}}{2})^k $$

וככל שהחזקה גבוהה יותר היחס בין האיברים העוקבים בסדרת פיבונאצ'י מתכנס ל-φ יחס הזהב:

$$ \lim_{{k \to \infty}} \frac{F_{k+1}}{F_{k}} \to \frac{1 + \sqrt{5}}{2} $$

למדריכים נוספים בסדרה על למידת מכונה

במדריך תכנות דינמי מלמטה למעלה ובחזרה - מדריך לתכנות דינאמי שמתחיל מהבסיס אפשר למצוא שיטה חישובית יעילה לחישוב מספרים בסדרת פיבונאצ'י באמצעות תכנות דינמי.

12 דברים שאתה חייב לדעת כשאתה עובד עם ספריית Numpy של Python

למידת מכונה בלתי מפוקחת באמצעות PCA

האצת למידת מכונה באמצעות שלב מקדים מבוסס טרנספורמציית PCA

לכל המדריכים בנושא של למידת מכונה

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים