למידת מכונה בלתי מפוקחת באמצעות PCA

ניתוח גורמים ראשיים Principal Component Analysis (PCA) היא טכניקה בה אנו משתמשים כדי להפחית את הממדיות (= מספר הפיצ'רים) של מערכי נתונים גדולים תוך שמירה על רוב השונות. כאשר, נא לזכור, השונות היא מה שמעניין אותנו במערך הנתונים. הפחתת מימדיות מקריבה דיוק ומעניקה פשטות. התוצאה היא נתונים פחות מדויקים, אבל כאלה שאנחנו יכולים בקלות לצייר מהם תרשים או להשתמש בהם כדי לאמן את המודלים שלנו בזמן קצר יותר. חשוב להבין, שהטכניקה לא משתמשת בממדים הקיימים אלא מארגנת את המידע באופן שיוצר ממדים חדשים קומפקטיים שמצליחים להכיל את המידע במספר מצומצם של ממדים דחוסים.

PCA הוא אחד האלגוריתמים הנפוצים ביותר עבור למידה לא מפוקחת. כשעושים אנליזת PCA המחשב מסווג את הנתונים לקבוצות בלי ידע מוקדם לגבי הקבוצות. למידה בלתי מפוקחת יכולה לספק תובנות מפתיעות על הנתונים. לדוגמה, מחקר רפואי שהתבסס על מספר גדול של מדדים מצא שהמדד שמצליח לחזות באופן הטוב ביותר את הסיכוי ללקות בהתקף לב הוא ירידה בעוצמה של לחיצת היד.

במדריך נעשה PCA באמצעות פונקציה של SciKit-Learn

יבוא הספריות ומסד הנתונים

נייבא את הספריות:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

נשתמש במסד נתונים המכיל אלפי תמונות של ספרות שאנשים רשמו בכתב ידם

from sklearn import datasets
df = datasets.load_digits()

כמה דוגמאות וכמה ממדים (פיקסלים) בכל דוגמה?

df.data.shape

(1797, 64)

• 1797 דוגמאות
• בכל אחת 64 ממדים כמספר הפיקסלים (במקור: תמונות של 8X8)

איך נראה המידע בכל תמונה?

df.data[0]

array([ 0.,  0.,  5., 13.,  9.,  1.,  0.,  0.,  0.,  0., 13., 15., 10.,
       15.,  5.,  0.,  0.,  3., 15.,  2.,  0., 11.,  8.,  0.,  0.,  4.,
       12.,  0.,  0.,  8.,  8.,  0.,  0.,  5.,  8.,  0.,  0.,  9.,  8.,
        0.,  0.,  4., 11.,  0.,  1., 12.,  7.,  0.,  0.,  2., 14.,  5.,
       10., 12.,  0.,  0.,  0.,  0.,  6., 13., 10.,  0.,  0.,  0.])

• מערך המכיל 64 פריטים
• ככל שהמספר גבוה יותר הפיקסל צבוע בגוון קרוב יותר לשחור (התמונות הם בשחור-לבן)

PCA מנסה לדחוס את המידע לכמות הנדרשת של ממדים. כל ממד הוא קומפוננטה עיקרית principal component כאשר הקומפוננטה הראשונה PC1 מכילה בתוכה הכי הרבה מידע מבין הקומפננטות PC2 היא השנייה מבחינת תכולת המידע וכיו"ב.

כשאנחנו מייחסים ל-PC תכולת מידע גבוהה אנחנו מתכוונים שנקודות המידע בו הם בעלות השונות הגבוהה ביותר בינם לבין עצמם וגם שהמידע נאמן למקור כי המרחק הגיאומטרי של כל נקודה בקומפוננטה הוא הקטן ביותר מהמידע המקורי.

נגדיר את המודל של sklearn כדי שידחוס את 64 הממדים לשניים הקומפקטיים ביותר:

from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X = pca.fit_transform(df.data)

כמה ממדים קיבלנו אחרי הפעלת ה-PCA?

X.shape

(1797, 2)

• שניים בלבד במקום 64 המקוריים.

נציג את 4 הדוגמאות הראשונות של פלט הפונקציה:

X[0:4, :]

array([[ -1.25947215,  21.27489244],
       [  7.9576063 , -20.76869962],
       [  6.99193049,  -9.95599322],
       [-15.90611352,   3.33247777]])

מכיוון שהפחתנו את מספר הממדים מ-64 ל-2 אנחנו יכולים להציג את התוצאה בקלות באמצעות תרשים דו ממדי:

plt.scatter(X[:,0], X[:,1]);

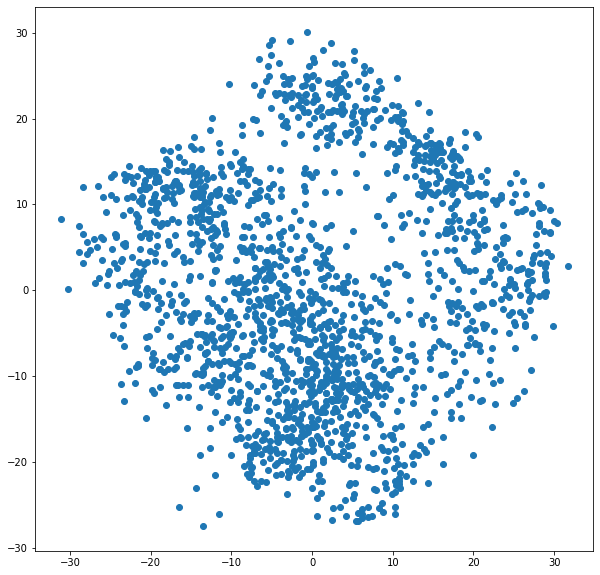
אחרי שקבלנו יצוג של הנתונים באופן שקל לנו להבין אנחנו צריכים להסביר את התוצאות כי זו למידה לא מפוקחת. לדוגמה, קבוצת הנקודות מימין לעומת הקבוצה משמאל ולהבין מה ההבדלים ביניהם.

במדריך בחרנו במסד נתונים המכיל תמונות של ספרות הכתובות בכתב יד אז ננסה לראות האם יש קשר בין היצוג הדו ממדי אותה פלטה פונקצית ה-PCA לבין תוכן התמונות.

מה התגיות של מסד הנתונים?

list(df.target_names)

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

• לא מפתיע כיוון שמסד הנתונים מכיל את הספרות 1-10 שכתבו אנשים.

נציין על גבי התרשים אילו ספרות רשומות בכל דוגמה:

plt.scatter(X[:,0],X[:,1],
            c=df.target,
            alpha=0.5)
plt.xlabel('component 1')
plt.ylabel('component 2')
plt.colorbar();

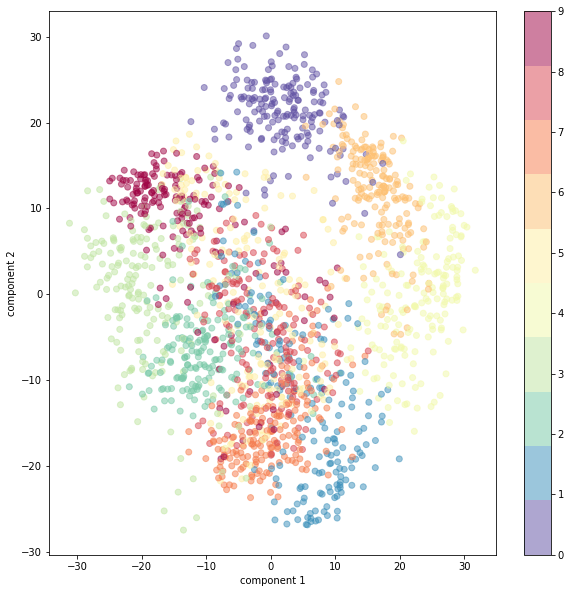
• למרות שירדנו מ-64 ממדים לשניים בלבד הדוגמאות מתקבצות לפי הספרות, האפסים מקובצים במעלה התרשים, האחדות בתחתית וכיו"ב.
• אפשר גם לראות קשרי גומלין. לדוגמה, שהאפסים מתקבצים ליד מקבצי התשיעיות והשישיות. כנראה בגלל שכולם מכילים עיגול.

מה שמדהים ששני ממדים במקום 64 מספיקים כדי לקבל תמונה די טובה של הנתונים. אם היינו בוחרים את 2 הפיקסלים הראשונים מתוך תמונה לא היינו מקבלים כזו תוצאה טובה. התוצאה מתאפשרת הודות ליכולת של אנליזת PCA לשלב ממדים קיימים וליצור חדשים שתכולת המידע שבהם גבוהה יותר מאשר המקור.

מזה אנחנו למדים שאחד הכוחות העיקריים של מודל PCA הוא ביכולת שלנו לקבל מידע שנוח להציג ולפרש אותו.

כמה ממדים?

ראינו שכדאי לנו להציג את הנתונים בשני ממדים בשביל שיהיה לנו קל לראות ולהסביר את התוצאות. גם מערך תלת ממדי יכול להיות מועיל ובתנאי שנוכל לסובב אותו. כשאנחנו משתמשים בגישה הזה אנחנו מאבדים המון מידע. כמה? התרשים הבא יעזור לנו להבין:

pca = PCA().fit(df.data)
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance');

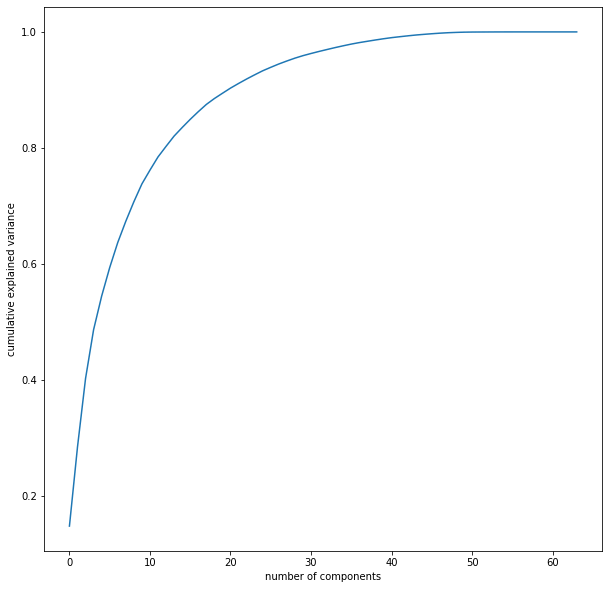
• על ציר ה-X מספר הקומפננטות ועל ציר ה-Y אחוז השונות המוסברת
• בשני ממדים כ-90% מהמידע המקורי הולך לאיבוד.
• וכדי לתפוס 80% מהמידע נצטרך 12 ממדים

מהתרגיל הזה אנחנו יכולים ללמוד שהרבה מידע הולך לאיבוד כשאנחנו מצמצמים את מספר הממדים וגם שזה לא נורא להפחית את מספר הממדים כי ה-PCA משאיר אותנו עם מידע ייחודי ופותר אותנו מהמידע החופף בין הממדים.

PCA הוא טכניקת למידת בלתי מפוקחת נפוצה בזכות קלות היישום והקלות היחסית של פרשנות התוצאות. בין השימושים: מציאת הקשרים החבויים בין דוגמאות המחקר, הפחתת רעשים, ודחיסת נתונים.

מקורות נוספים אודות PCA

גם זה יעניין אותך

• מודלים ללמידת מכונה של SciKit-Learn
• האצת למידת מכונה באמצעות שלב מקדים מבוסס טרנספורמציית PCA
• ניקוי תמונות מרעשים באמצעות למידת מכונה

לכל המדריכים בנושא של למידת מכונה

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים