מדריך הסתברות מעריכית (אקספוננציאלית) מהלכה למעשה עם פייתון

התפלגות מעריכית (אקספוננציאלית) מתארת את הזמן החולף בין אירועים המתרחשים בקצב קבוע ללא תלות באירועים קודמים.

דוגמאות לאירועים המתפלגים מעריכית הינם: הזמן במילישניות בין התפרקויות רדיואקטיביות, הזמן בדקות עד למענה לשיחות במוקד שיחות, הזמן בשעות בין לחיצות על לינק בדף אינטרנט, או הזמן בשנים בין רעידות אדמה.

התפלגות מעריכית (אקספוננציאלית) מתארת משתנים רציפים (יכולים לקבל כל ערך בטווח) וחיוביים. היא מתארת את הזמן החולף בין אירועים המתרחשים בקצב קבוע ללא תלות באירועים קודמים. עצמאות זו מאירועים קודמים הופכת את ההסתברות המעריכית לחסרת זכרון. ההתפלגות המעריכית שימושית לניתוח זמני המתנה, לחיזוי אירועים עתידיים, ותכנון מערכות.

את ההסתברות המעריכית מאפיין פרמטר אחד, μ, זמן ההמתנה הממוצע, כאשר בזמן ארוך מספיק הזמן הממוצע עד להתרחשות אירוע מתכנס לערך הפרמטר μ.

זמן ההמתנה הממוצע, μ, קובע את צורת פונקציית הצפיפות (PDF) של ההתפלגות. להלן מספר דוגמאות:

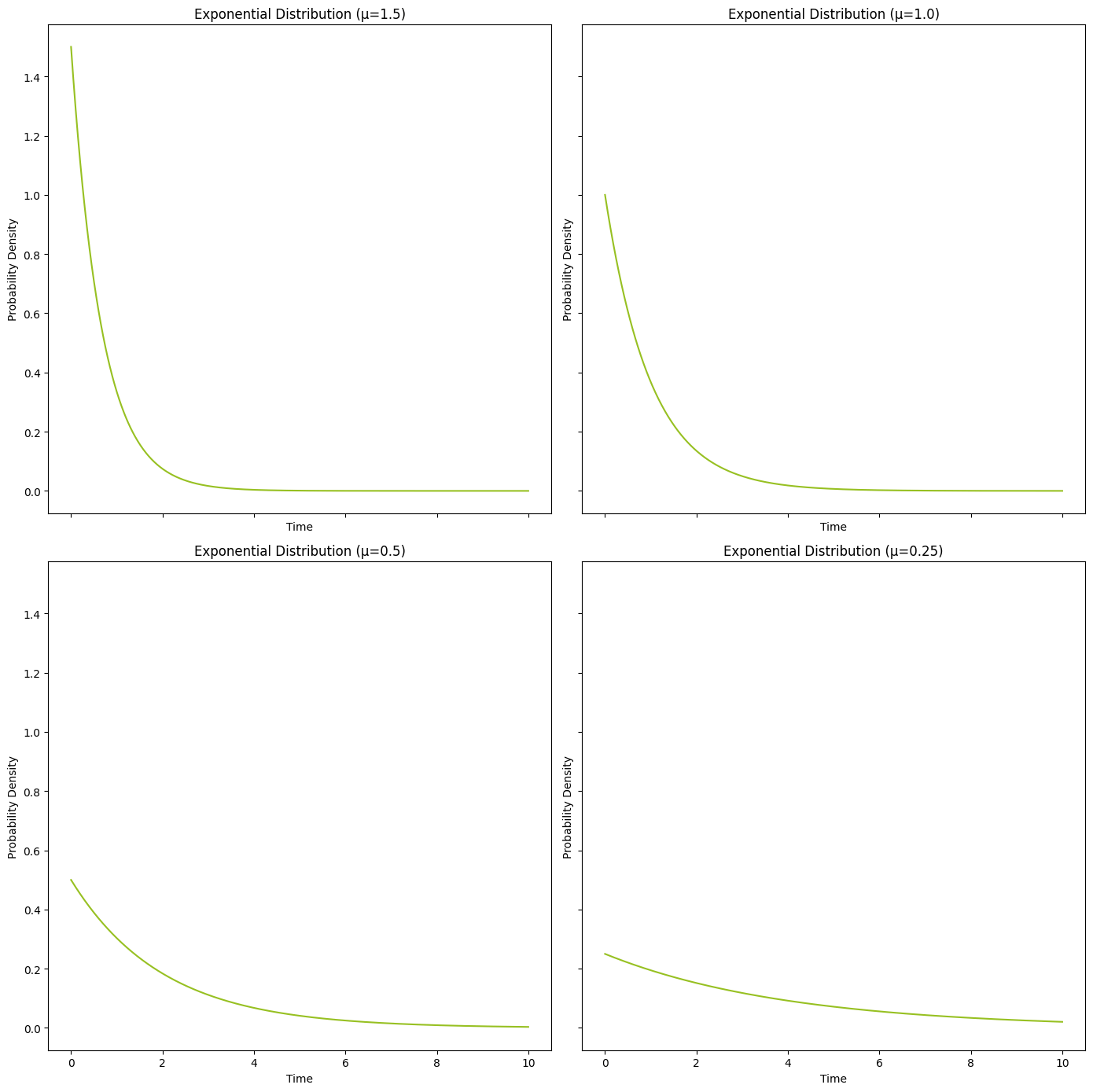
מגרף פונקציית הצפיפות (PDF) של ההתפלגות המעריכית ניתן ללמוד מספר תובנות מרכזיות:

• ציר ה-x: נתון ביחידות זמן. לדוגמה, minute או year. המשתנה הבלתי תלוי x מייצג את משך הזמן בין האירועים והוא משתרע בין 0 לאינסוף.

• ציר ה-y: הערך המקסימלי של צפיפות ההסתברות המיוצג בציר ה-y מתחיל בערכו המקסימלי ויורד ככל ש-x גדל. הערך המקסימלי בציר y שווה ל-זמן ההמתנה הממוצע, μ.

• השפעת μ על שיעור הירידה המקסימלי: זמן ההמתנה הממוצע, μ, שולט בצורה של ההתפלגות המעריכית. ערך גבוה יותר של μ מתאים לירידה תלולה יותר בעקומת ה-PDF. זה מצביע על כך שככל ש-μ גדול יותר, פחות סביר שיתרחשו אירועים ככל שהזמן חולף, מה שמוביל לירידה מהירה יותר בפונקציית צפיפות ההסתברות.

• ירידה מעריכית (אקספוננציאלית): ההתפלגות המעריכית מציגה דפוס דעיכה מעריכי אופייני, שבו צפיפות ההסתברות פוחתת מעריכית ככל שערך המשתנה המקרי ( x ) עולה. ירידה זו היא רציפה ואינה מגיעה לעולם לאפס, שכן ההתפלגות משתרעת לאינסוף ימינה.

• השטח מתחת לעקומה: השטח הכולל מתחת לעקומת ה-PDF שווה ל-1, ומייצג את ההסתברות הכוללת של כל התוצאות האפשריות. תכונה זו מבטיחה שההתפלגות המעריכית מנורמלת כהלכה, מה שהופך אותה מתאימה לחישובי הסתברות והסקה.

התפלגות מעריכית והתפלגות פואסון

התפלגות מעריכית קשורה בקשר ישיר להתפלגות פואסונית. בעוד התפלגות פואסונית מתארת את מספר האירועים שקורים בטווח זמן קבוע, התפלגות מעריכית מתארת את מרווח הזמן בין אירועים עוקבים.

הפרמטר λ (למדא) מאפיין את שתי ההתפלגויות, מעריכית ופואסונית. במקרה התפלגות פואסונית λ מתארת את מספר האירועים הממוצע שקרו בטווח זמן קבוע. במקרה של התפלגות מעריכית μ (mu) מתאר את הזמן הממוצע בין אירועים כאשר μ = 1/λ. במילים, הפרמטר μ שווה להופכי של λ.

ניתן להדגים את הקשר בין התפלגות פואסונית והתפלגות מעריכית באמצעות צומת דרכים והמכוניות העוברות דרכה.

התפלגות פואסונית יכולה לחזות את מספר המכוניות שיעברו בצומת תוך דקה אחת (λ מכוניות/דקה) כאשר λ תלויה בצפיפות התנועה הממוצעת ובקצב הזרימה.

לעומת זאת, התפלגות מעריכית יכולה לתאר את הזמן בדקות בין מעברן של שתי מכוניות זו אחר זו בצומת.

לדוגמה, אם קצב המעבר הממוצע הוא 10 מכוניות בדקה (λ = 10), זמן ההמתנה הממוצע בין המכוניות הוא 1/10 דקה (=6 שניות).

צריך לשים לב שככל שקצב הגעת המכוניות (λ) גבוה יותר, כך מספר המכוניות בדקה גבוה יותר (פואסונית), אך זמן ההמתנה (μ) ביניהן קצר יותר (מעריכית).

נראה דוגמה נוספת לקשר בין ההתפלגויות.

ניתן להדגים את הקשר בין התפלגות פואסונית ומעריכית באמצעות מספר המבקרים שיקליקו על לינק לרכישת מוצר בדף אינטרנט בשעה.

התפלגות פואסון יכולה לחזות את מספר ההקלקות העתידיות ביום (λ הקלקות/יום). זה תלוי בגורמים כמו הפופולריות של האתר וקמפיינים פרסומיים.

כדי להעריך כמה זמן בממוצע יש לחכות להקלקה הבאה על הלינק, נוכל להיעזר בהתפלגות מעריכית אשר מחשבת את מספר הימים עד להקלקה הבאה (μ ימים).

אם קצב ההקלקה הממוצע הוא 48 הקלקות ביום (λ = 48), הזמן הממוצע בין הקלקלה אחת לבאה אחריה הוא 1/48 ימים (שזה יוצא חצי שעה בממוצע).

צריך לשים לב לקשר ההפוך, כאשר יותר מקליקים ביום בממוצע משמעו λ גבוה (פואסון), אבל גם זמני המתנה ממוצעים μ קצרים יותר בין הקלקות (מעריכית).

בשביל לתאר נתונים המתפלגים פואסונית כל מה שאנחנו צריכים לדעת הוא את ערך הפרמטר λ.

אנחנו יכולים להיעזר בשפת פייתון (או בכל תוכנה סטטיסטית) כדי לתאר בגרף את ההתפלגות הפואסונית עבור λ מסויים.

לדוגמה ידוע שמספר הקלקות ללינק מסוים בדף אינטרנט בשעה מתפלג פואסונית, כאשר λ = 10 הקלקות לשעה.

את התפלגות הנתונים נתאר באמצעות הגרף הבא אותו ניצור בעזרת קוד פייתון:

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson

# Parameters for Poisson distribution
lambda_poisson = 10

# Generate x values for plotting
x_values_poisson = np.arange(0, 20)
x_values_exponential = np.linspace(0, 20, 1000)

# Calculate Poisson Probability
poisson_probs = poisson.pmf(x_values_poisson, lambda_poisson)

# Plot Poisson distribution
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.bar(x_values_poisson, poisson_probs, color='#97c022')
plt.title('Poisson Distribution (λ=10)')
plt.xlabel('Number of Events')
plt.ylabel('Probability')

plt.tight_layout()
plt.show()

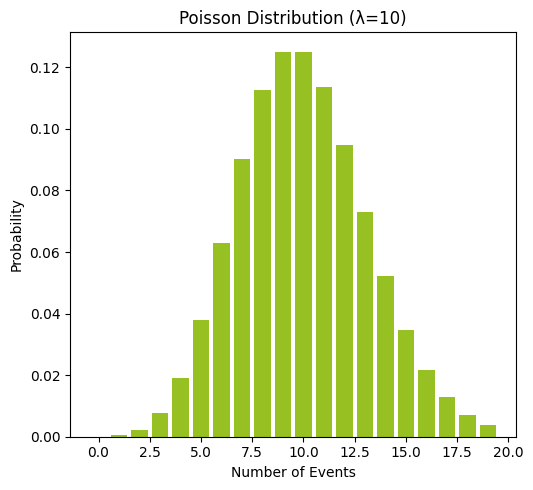
• PMF, פונקציית הצפיפות, משמש לתיאור התפלגות נתונים בדידים (דוגמת מספר הקלקות על לינק בדף אינטרנט בשעה).

• ציר ה-x מתאר את מספר ההקלקות בשעה. ציר ה-y מתאר את השכיחות.

• התפלגות הנתונים עבור λ=10 מלמד שהערך השכיח הוא 10 (וכך גם הערך הצמוד לו 9). הסתברות הערכים 9 ו-10 היא קצת יותר מ-13%.

• ככל שאנחנו מתרחקים ממרכז ההתפלגות כך השכיחות פוחתת.

• הערכים אינם יכולים להיות שליליים.

נשווה את גרף ההתפלגות הפואסונית כאשר λ=10 למצב המקביל בו ההתפלגות האקספוננציאלית מאופיינת ב-μ=1/10:

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson, expon

# Parameters for Poisson distribution
lambda_poisson = 10

# Parameters for Exponential distribution
mu_exponential = 1 / lambda_poisson

# Generate x values for plotting
x_values_poisson = np.arange(0, 20)
x_values_exponential = np.linspace(0, 20, 1000)

# Calculate Poisson and Exponential probabilities
poisson_probs = poisson.pmf(x_values_poisson, lambda_poisson)
exponential_probs = expon.pdf(x_values_exponential, scale=1/mu_exponential)

# Plot Poisson distribution
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.bar(x_values_poisson, poisson_probs, color='#97c022')
plt.title('Poisson Distribution (λ=10)')
plt.xlabel('Number of Events')
plt.ylabel('Probability')

# Plot Exponential distribution
plt.subplot(1, 2, 2)
plt.plot(x_values_exponential, exponential_probs, color='#97c022')
plt.title('Exponential Distribution (μ=1/10)')
plt.xlabel('Time')
plt.ylabel('Probability Density')

plt.tight_layout()
plt.show()

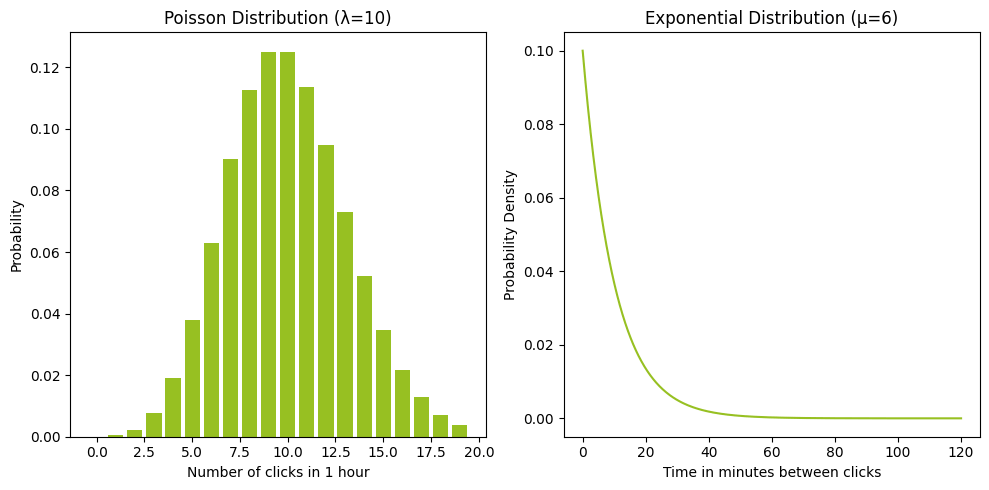
• בעוד התפלגות פואסון המוצגת בגרף משמאל מתארת נתונים בדידים (מספר הקלקות בשעה) מתארת ההתפלגות המעריכית בגרף מימין את מספר הדקות בין ההקלקות כשנתון זה הינו רציף ולא בדיד. הסיבה להבדל היא שאין דבר כזה חצי הקלקה אבל יכולה לעבור חצי שעה בין הקלקות.

• נתונים בדידים דוגמת נתונים המתפלגים פואסונית מתוארים באמצעות גרף PMF (Probability Mass Function) בעוד נתונים המשכיים דוגמת נתונים המתפלגים מעריכית מתוארים באמצעות גרף PDF (Probability Density Function).

• בעוד ההתפלגות הפואסונית מאופיינת בממוצע λ=10 ההתפלגות האקספוננציאלית מאופיינת בממוצע שהינו בדיוק המספר ההופכי μ=1/10 והסיבה היא שאם מספר ההקלקות הוא 10 בשעה אז זה אומר שתחלוף כעשירית השעה בין הקלקות עוקבות. כאשר עשירית השעה שווה 6 דקות.

• גרף ההתפלגות המעריכית מתאר אירועים שביניהם חולפות חלקי שעות ועל כן ציר ה-x יתאר את מספר הדקות בין האירועים (ולא שעות) וזה בגלל שיותר נוח להסתכל על דקות מאשר על שעות כאשר רוצים לתאר חלקים של שעות.

• הערך המקסימלי של גרף ההתפלגות האקספוננציאלית הוא μ. שבמקרה שלנו ערכו 0.1 שעות או 6 דקות.

• הערך השכיח של גרף ההתפלגות הפואסונית הוא λ. שבמקרה שלנו ערכו 10.

נוסף לפונקציית הצפיפות PDF חשוב להכיר את פונקציית ההסתברות המצטברת (CDF = Cumulative Distribution Function) עבור התפלגות פואסון והתפלגות מעריכית:

# Parameters for Poisson distribution
lambda_poisson = 10

# Parameters for Exponential distribution
mu_exponential = 1 / lambda_poisson

# Generate x values for plotting
x_values_poisson = np.arange(0, 20)
x_values_exponential = np.linspace(0, 120, 1000)

# Calculate Poisson and Exponential CDFs
poisson_cdf = np.cumsum(poisson.pmf(x_values_poisson, lambda_poisson))
exponential_cdf = expon.cdf(x_values_exponential, scale=1/mu_exponential)

# Plot Poisson distribution
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.bar(x_values_poisson, poisson_cdf, color='#97c022')
plt.title('Poisson Distribution CDF (λ=10)')
plt.xlabel('Number of clicks in 1 hour')
plt.ylabel('Cumulative Probability')

# Plot Exponential distribution
plt.subplot(1, 2, 2)
plt.plot(x_values_exponential, exponential_cdf, color='#97c022')
plt.title('Exponential Distribution CDF (μ=6)')
plt.xlabel('Time in minutes between clicks')
plt.ylabel('Cumulative Probability')

plt.tight_layout()
plt.show()

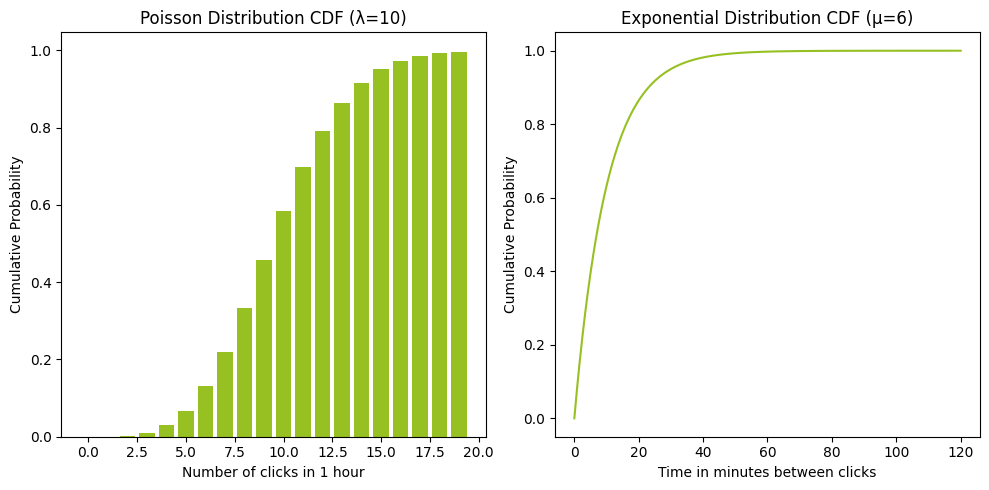
• ככל שמתקדמים משמאל לימין על ציר ה-x כך הערך המצטבר בציר ה-y מתקרב ל-1. לדוגמה, אם נסתכל על ה-CDF של ההתפלגות המעריכית של מספר הקלקות בדקה נוכל לראות שכבר אחרי 40 דקות ההסתברות להקלקלה הינו קרוב מאוד ל-1. וב-60 דקות ההסתברות היא כבר 1, ומעבר לזה כבר אי אפשר (כי הסתברות תחומה בין 0 ל-1).

פונקציית ההסתברות המצטברת CDF מתקבלת מאינטגרציה של פונקצית הצפיפות PDF:

1. פונקציית הצפיפות של ההתפלגות האקספוננציאלית מתוארת באמצעות:

   $$ f(x) = \lambda e^{-\lambda x} $$

2. פונקציית ההסתברות המצטברת CDF עבור משתנה X מתקבלת מחישוב סך ערכי ה-PDF הקטנים מ-X. נחשב את הסה"כ המצטבר באמצעות אינטגרציה היות והפונקציה רציפה:

   $$ F(x) = \int_{0}^{x} \lambda e^{-\lambda t} dt $$

   • אנחנו משתמשים ב-t כדי להבדיל בינו לבין x.

3. נוציא את הקבוע λ מחוץ לאינטגרל, נפעיל את נוסחת האינטגרל, ונפשט את התוצאה:

   $$ \lambda \int_{0}^{x} e^{-\lambda t} dt = \lambda \left(\frac{1}{-\lambda} e^{-\lambda t}\right) + C = -e^{-\lambda t} + C $$

4. ניישם את גבולות האינטגרציה:

   $$ - e^{-\lambda t} \Bigg|_{0}^{x} = - e^{-\lambda x} + e^{0} = 1 - e^{-\lambda x} $$

המסקנה היא שפונקציית ה-CDF, התפלגות מצטברת, של ההתפלגות האקספוננציאלית נתונה ע"י הנוסחה:

$$ F(x) = 1 - e^{-\lambda x} $$

• להבא, נשתמש בנוסחת ה-CDF לצורך החישובים של ההתפלגויות המצטברות במקום לעשות אינטגרציה של פונקציית ה- PDF, פונקצית הצפיפות, בכל פעם שנרצה לחשב את ההתפלגויות המצטברות.

תכונות נוספות של ההתפלגות המעריכית

ממוצע ההתפלגות:

$$ Mean = \frac{1}{\lambda} $$

• כדי להבין את הסיבה תחשוב על התרחיש שבו דף אינטרנט מקבל ממוצע של שני מבקרים בכל שעה מה שאומר שבכל חצי שעה בממוצע נכנס מבקר אחד.

שונות ההתפלגות האקספוננציאלית:

$$ Var = \frac{1}{\lambda^2} $$

מה שאומר שסטיית התקן שווה לממוצע כי מחשבים אותה על ידי הוצאת שורש לשונות:

$$ Stdev = \sqrt{\frac{1}{\lambda^2}} = \frac{1}{\lambda^2} $$

הערך השכיח הוא אפס:

$$ Mode = 0 $$

• לא מפתיע שהערך השכיח הוא אפס בגלל שההסתברות היא הגבוהה ביותר ב- x=0 , והיא פוחתת ככל ש-x גדל. כתוצאה מכך, לכל ערך אחר של x תהיה הסתברות נמוכה יותר.

שאלות להעמקת ההבנה של התפלגות אקספוננציאלית

ידוע שלקוחות מגיעים לחנות בקצב של 4 לקוחות בשעה. בהנחה שהגעת הלקוחות מתפלגת באופן מעריכי (אקספוננציאלי), מצא את ההסתברות שהלקוח הבא יגיע לחנות:

1. לפני 10 דקות.

2. אחרי 10 דקות.

3. בין 10 ל-20 דקות.

4. בדיוק בדקה ה-15.

5. באיזה דקה צפויים להגיע מחצית הלקוחות? ובאיזו דקה צפויים להגיע 90% מהלקוחות?

תשובות

אם ידוע שחולפים בממוצע 15 דקות בין הגעת לקוחות אז זה אומר שקצב הגעת הלקוחות הוא 1 ל-15 דקות:

$$ \mu = 15 min \\ \lambda = \frac{1}{15} min^{-1} $$

1. ביקשו מאיתנו למצוא את ההסתברות להגעת לקוח לפני הדקה העשירית. כדי לפתור נציב ערך של x בנוסחת ההתפלגות המצטברת של ההתפלגות המעריכית:

   $$ P(X < x) = 1 - e^{-\lambda x} $$

   כאשר x = 10:

   $$ P(X < 10) = 1 - e^{-\frac{1}{15} * 10} = 0.487 $$

   המסקנה היא שההסתברות P להגעת הלקוח הבא לחנות לפני 10 דקות היא 0.487

   לאותה מסקנה אנחנו יכולים להגיע על ידי שימוש בקוד פייתון. נשתמש בפונקציה scipy.stats.expon.cdf() לצורך חישוב ההסתברויות המצטברות עד לדקה העשירית:

   from scipy.stats import expon
   
   # Given parameter
   lamda = 4 / 60  # customers per minute (mean of 15 minutes between customers arrival)
   
   # (1) Probability of arrival before 10 minutes
   prob_before_10_min = expon.cdf(10, scale=1/lamda)
   
   print("(1) Probability of arrival before 10 minutes:", prob_before_10_min)

   התוצאה:

   (1) Probability of arrival before 10 minutes: 0.486582880967408

   קוד הפייתון הבא מציג את עקומת הצפיפות שהשטח תחתיה הוא הסתברות ההגעה לפני הזמן הנתון. במקרה זה, השטח המוצלל מציין את ההסתברות המצטברת עד ל-10 דקות:

   import numpy as np
   from scipy.stats import expon
   import matplotlib.pyplot as plt
   
   # Given parameters
   lamda = 4 / 60 # rate parameter, 4 customers in 60 minutes
   
   # Generate x values for plotting
   x_values = np.linspace(0, 120, 1000)  # 0 to 120 minutes for plotting
   
   # Calculate the cumulative probabilities
   pdf_values = expon.pdf(x_values, scale=1/lamda)
   
   # Plot PDF
   plt.figure(figsize=(8, 6))
   plt.plot(x_values, pdf_values, color='#97c022')
   
   # Shade the area until the 10th minute
   plt.fill_between(x_values, pdf_values, where=(x_values <= 10), color='#97c022', alpha=0.5)
   
   # Labels and title
   plt.title('Probability Density Function (PDF) of Arrival Time')
   plt.xlabel('Time (minutes)')
   plt.ylabel('Cumulative Probability')
   plt.grid(True)
   plt.show()

   התוצאה:

   

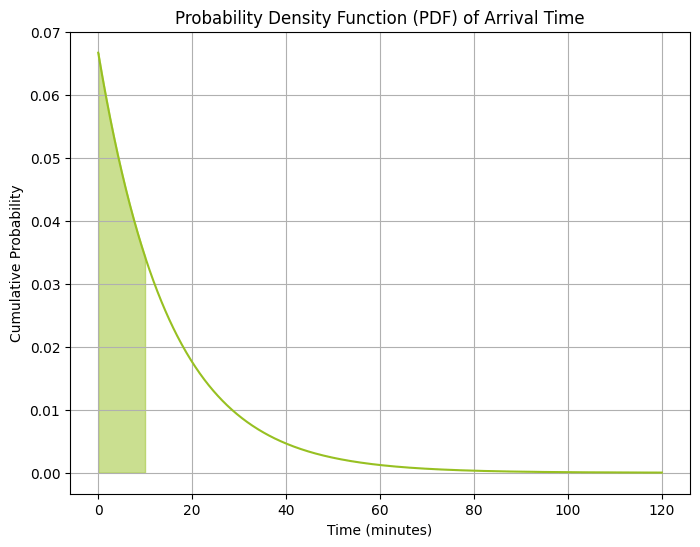
   את החישוב עצמו לא עשינו באמצעות אינטגרציה של השטח מתחת לעקומת ה-PDF אלא על סמך הערך של עקומת ה-CDF בנקודה בה x=10:

   # Given parameter
   lamda = 4 / 60 # rate parameter, 4 customers in 60 minutes
   
   times = np.linspace(0, 30, 200)  # Create array of times (in minutes)
   probabilities = expon.cdf(times, scale=1/lamda)
   
   plt.plot(times, probabilities, color='#97c022')
   plt.xlabel("Time (minutes)")
   plt.ylabel("Probability of Arrival")
   plt.title("CDF of Exponential Distribution for Customer Arrival")
   plt.axhline(y=prob_before_10_min, color='#504e4f', linestyle='--') # Horizontal line at P = prob_before_10_min
   plt.axvline(x=10, color='#504e4f', linestyle='--')  # Vertical line at 10 minutes
   plt.show()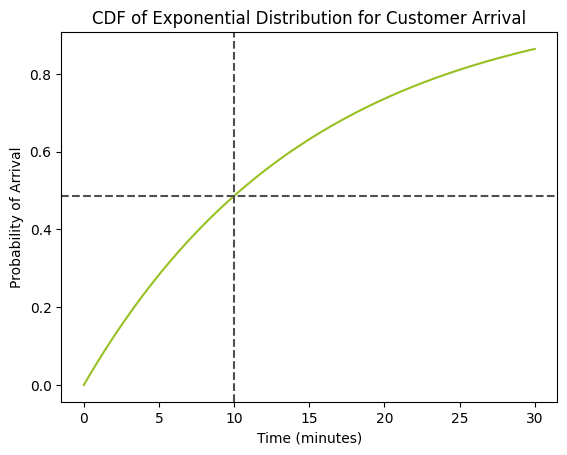

   

2. ביקשו מאיתנו לחשב את ההסתברות להגעת לקוח אחרי הדקה העשירית. במקום לחשב את הערכים מ-10 דקות ועד לאינסוף כיוון שעל ציר ה -x ההתפלגות המעריכית נמשכת עד אינסוף, נשתמש בידע על כך שסכום ההתפלגויות המצטברות חייב להיות 1, ולפיכך נפחית את הערך של עד x שמעניין אותנו מ-1 כדי לקבל את התשובה:

   $$ P(X > x) = 1 - P(X < x) \\ = 1 - \left(1 - e^{-\lambda x}\right) \\ = 1 - 1 + e^{-\lambda x} $$

   לפיכך, הנוסחה למציאת פונקציית ההתפלגות המעריכית המצטברת עבור ערכים של x הגדולים מערך הסף הינה:

   $$ P(X > x)= e^{-\lambda x} $$

   נציב את הערכים של x = 10 ו-λ:

   $$ P(X > 10) = e^{-\frac{1}{15} * 10} = e^{-\frac{2}{3}} = 0.513 $$

   המסקנה היא שההסתברות P להגעת הלקוח הבא לחנות אחרי 10 דקות היא 0.513

   דבר נוסף שצריך לשים אליו הוא שההסתברות להגעת לקוח לפני 10 דקות אותה חישבנו בסעיף הראשון (P = 0.487) בתוספת ההסתברות להגעת הלקוח אחרי 10 דקות אותה חישבנו בסעיף הנוכחי (P = 0.513) שווה ל-1:

   $$ 0.513 + 0.487 = 1 $$

   תוצאה מתבקשת היות וסך כל ההסתברות הוא בהגדרה 1, והמשלים של התרחשות אירוע לפני 10 דקות הוא התרחשות אותו אירוע אחרי 10 דקות.

   ניתן להגיע לאותה תוצאה באמצעות פייתון:

   # Given parameter
   lamda = 4 / 60  # customers per minute (mean of 15 minutes between customers arrival)
   
   # (2) Probability of arrival after 10 minutes
   prob_after_10_min = 1 - prob_before_10_min

   התוצאה:

   (2) Probability of arrival after 10 minutes: 0.513417119032592

   החלק המוצלל תחת עקומת הצפיפות המתארת את ההתפלגות המעריכית מייצג את ההסתברות להגעת לקוח אחרי הדקה העשירית, והוא לא במקרה מהווה את המשלים של ההסתברות להגעת לקוח לפני הדקה העשירית:

   # Given parameter
   lamda = 4 / 60 # rate parameter, 4 customers in 60 minutes
   
   # Generate x values for plotting
   x_values = np.linspace(0, 120, 1000)  # 0 to 120 minutes for plotting
   
   # Calculate the cumulative probabilities
   pdf_values = expon.pdf(x_values, scale=1/lamda)
   
   # Plot PDF
   plt.figure(figsize=(8, 6))
   plt.plot(x_values, pdf_values, color='#97c022')
   
   # Shade the area following the 10th minute
   plt.fill_between(x_values, pdf_values, where=(x_values > 10), color='#97c022', alpha=0.5)
   
   # Labels and title
   plt.title('Probability Density Function (PDF) of Arrival Time')
   plt.xlabel('Time (minutes)')
   plt.ylabel('Cumulative Probability')
   plt.grid(True)
   plt.show()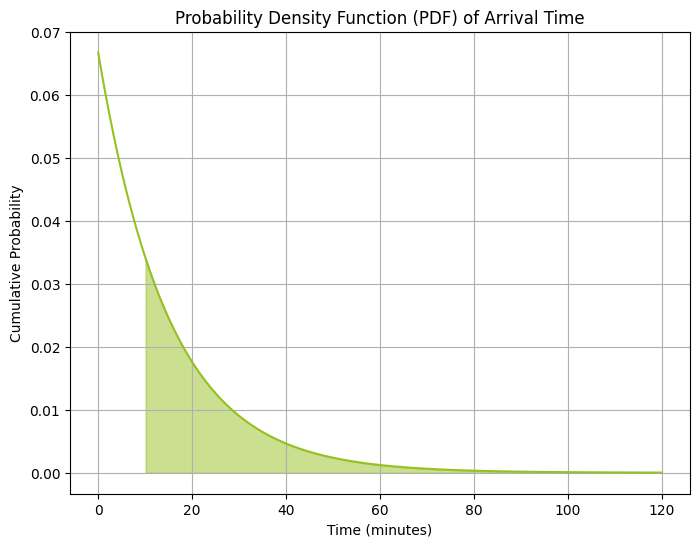

   

3. השאלה מבקשת מאיתנו לחשב את ההסתברות להגעת הלקוח הבא בין הדקה העשירית והעשרים.

   $$ P(x_1 < X < x_2) = e^{-\lambda x_1} - e^{-\lambda x_2} $$

   נציב את הערכים:

   • $$ \lambda = \frac{1}{15} $$

   • $$ x_2 = 20 $$

   • $$ x_1 = 10 $$

   ונפתור:

   $$ P(x_1 < X < x_2) = e^{-\frac{1}{15} 10} - e^{-\frac{1}{15} 20} \\ e^{-\frac{2}{3}} - e^{-\frac{4}{3}} = 0.25 $$

   נגיע לאותה התוצאה באמצעות פייתון:

   # Given parameter
   lamda = 4 / 60  # customers per minute (mean of 15 minutes between customers arrival)
   
   # (3) Probability of arrival between 10 and 20 minutes
   prob_between_10_20_min = expon.cdf(20, scale=1/lamda) - expon.cdf(10, scale=1/lamda)
   
   
   
   # Generate x values for plotting
   x_values = np.linspace(0, 120, 1000)  # 0 to 120 minutes for plotting
   
   # Calculate the cumulative probabilities
   pdf_values = expon.pdf(x_values, scale=1/lamda)
   
   # Plot CDF
   plt.figure(figsize=(8, 6))
   plt.plot(x_values, pdf_values, color='#97c022')
   
   # Shade the area after the 10th minute and before the 20th
   plt.fill_between(x_values, pdf_values, where=((x_values> 10) & (x_values < 20)), color='#97c022', alpha=0.5)
   
   # Labels and title
   plt.title('Probability Density Function (PDF) of Arrival Time')
   plt.xlabel('Time (minutes)')
   plt.ylabel('Cumulative Probability')
   plt.grid(True)
   plt.show()

   (3) Probability of arrival between 10 and 20 minutes: 0.2498199809168653

   

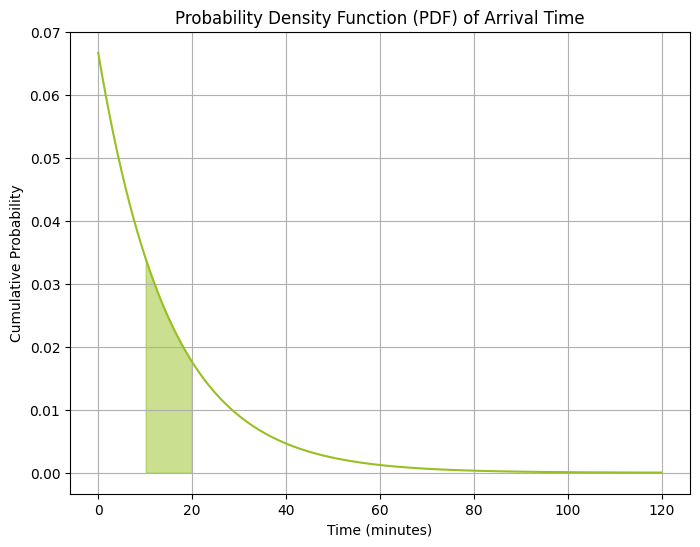
4. בהתפלגויות המתארות הסתברויות רציפות, כמו ההתפלגות המעריכית, הרעיון של הסתברות שמאורע יתרחש בזמן מדויק חסר משמעות מעשית כיוון שהתפלגויות אלו נועדו לתיאור הסתברויות על פני מרווחי זמן ולא מקרים בדידים (להבדיל מהסתברויות בדידות). כתוצאה מכך, צפיפות ההסתברות בכל נקודת זמן מדויקת היא תמיד אפס, דבר המשקף את הסבירות הזעירה להתרחשות מדויקת של אירוע.

   אם קשה לך להבין את זה אז תחשוב לרגע על לקוח שמגיע לחנות בדיוק תוך 15 דקות. אבל ממש בדיוק. על אלפית השנייה אפילו מיליונית. האם זה סביר? ודאי שלא כי תמיד ימצא טווח זמן קצר יותר כך שאי אפשר להגדיר בדיוק.

   כדי להתמודד עם חוסר היכולת המובנה של התפלגויות רציפות לחשב הסתברויות בדידות, אנחנו יכולים ליצור מרווחים זעירים סביב נקודת הזמן הרצויה. לדוגמה, בתרחיש שלנו, נוכל לבחור טווח צר, כמו 0.01 שניות לפני ואחרי הדקה ה-15, כדי לחשב את ההסתברות. על ידי קביעת השטח מתחת לעקומת ההתפלגות בתוך מרווח זעיר זה, אנו מקבלים מדידה משמעותית של ההסתברות המשויכת למסגרת הזמן הספציפית בתוספת שוליים זעירים סביבה.

5. במקרה זה נתונה לנו ההסתברות (P = 0.5), ומה שאנחנו צריכים למצוא הוא את משך הזמן אותו צריך למשוך (x) עד לקיום ההסתברות.

   נתון:

   $$ \lambda = \frac{1}{15} \\ P(x < k) = 0.5 $$

   אנחנו מכירים את הנוסחה לחישוב הסתברות מעריכית:

   $$ P = 1 - e^{-\lambda x} $$

   נעביר אגפים כדי שיהיה לנו יותר נוח לעבוד עם לוגים בהמשך:

   $$ e^{-\lambda x} = 1 - P $$

   נפעיל את הלוג הטבעי של e על שני האגפים כדי להפתר מהחזקה ולאפשר מעבר למשוואה ליניארית שנוח לעבוד איתה:

   $$ -\lambda x * ln(e) = ln(1 - P) $$

   נפעיל את הלוג על e ונקבל 1:

   $$ -\lambda x * 1 = ln(1 - P) $$

   נציב את ערכי הקבועים הידועים לנו λ והסתברות P:

   $$ -\frac{1}{15} x = ln(1 - 0.5) = ln(0.5) $$

   נבודד את x, ונחשב:

   $$ x = -15 * ln(0.5) \\ x = 10.4 $$

   המסקנה היא שמחצית הלקוחות צפויים להגיע תוך 10.4 דקות.

   • הסתברות של 0.5 משמעותה שהחציון הוא 10.4 במקרה שלנו.

    

   כדי לחשב את זמן ההגעה של 90% מהלקוחות נציב את ההסתברות של 0.9 במקום 0.5 ותוצאת החישוב תהיה שמשך הזמן הממוצע עד להגעת 90% מהלקוחות הוא 34.54 דקות.

    

   את החישובים אפשר לעשות באמצעות שפת התכנות פייתון. לשם כך, נשתמש בפונקצייה scipy.stats.expon.ppf (Percent Point Function) שעושה את הפעולה ההפוכה לפונקציית ההסתברות המצטברת (scipy.stats.expon.cdf). בעוד הפונקציה cdf() מחשבת את ההסתברות שמאורע יתרחש לפני זמן מסויים, הפונקציה ppf() מחשבת את משך הזמן הנדרש להגעה להסתברות נתונה.

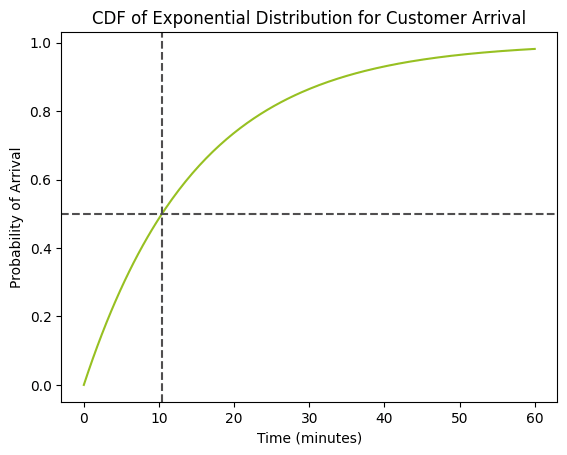
   # Parameters
   lamda = 1/15  # Events per minute
   mu = 1/lamda  # Mean time between events (minutes)
   
   # Calculate the average time for 50% of customers to arrive
   average_time = expon.ppf(0.5, scale=mu)
   print(f"Average time for 50% of customers to arrive is {average_time:.3f} minutes") 
   
   # Create more granular array of times for smoother plot
   times = np.linspace(0, 4 * mu, 200)  
   probabilities = expon.cdf(times, scale=mu)
   
   # Plotting
   plt.plot(times, probabilities)
   plt.xlabel("Time (minutes)")
   plt.ylabel("Probability of Arrival")
   plt.title("CDF of Exponential Distribution for Customer Arrival")
   plt.axhline(y=0.5, color='red', linestyle='--') 
   plt.axvline(x=average_time, color='red', linestyle='--')
   plt.show()

   התוצאה:

   Average time for 50% of customers to arrive is 10.397 minutes

   

    

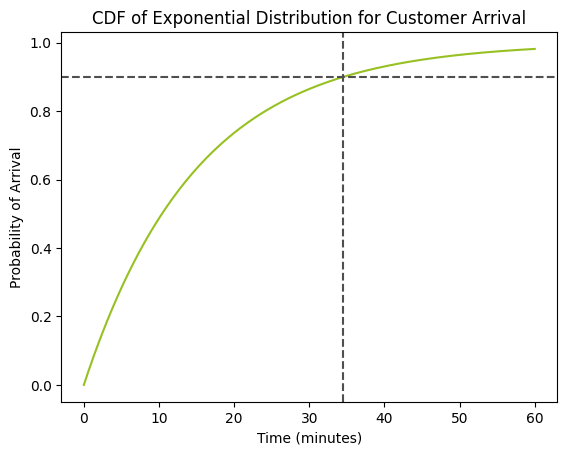
   # Parameters
   lamda = 1/15  # Events per minute
   mu = 1/lamda  # Mean time between events (minutes)
   
   # Calculate the average time for 90% of customers to arrive
   average_time = expon.ppf(0.9, scale=mu)
   print(f"Average time for 90% of customers to arrive is {average_time:.3f} minutes") 
   
   # Create more granular array of times for smoother plot
   times = np.linspace(0, 4 * mu, 200)  
   probabilities = expon.cdf(times, scale=mu)
   
   # Plotting
   plt.plot(times, probabilities)
   plt.xlabel("Time (minutes)")
   plt.ylabel("Probability of Arrival")
   plt.title("CDF of Exponential Distribution for Customer Arrival")
   plt.axhline(y=0.9, color='red', linestyle='--') 
   plt.axvline(x=average_time, color='red', linestyle='--')
   plt.show()

   התוצאה:

   Average time for 90% of customers to arrive is 34.539 minutes

   

מדריכים נוספים בסדרה על למידת מכונה שעשויים לעניין אותך

12 דברים שאתה חייב לדעת כשאתה מייצר תרשימים באמצעות matplotlib של python

מדריך מעשי על התפלגות פואסנית באמצעות קוד פייתון וציפורים נודדות

התפלגות בינומית - הלכה למעשה

לכל המדריכים בנושא של למידת מכונה

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים