התפלגות בינומית - הלכה למעשה

התפלגות בינומית היא אחת התפלגויות הנפוצות בתחום הסטטיסטיקה. במדריך נטעם מההתפלגות הבינומית בעזרת דוגמה טעימה במיוחד, ונקנח עם קוד פייתון.

דמיינו שאתם בעלי מאפיית עוגיות, וזה עתה הוספתם מוצר חדש: עוגיות מקרון. אתם שמים לב שבממוצע, 20% מהלקוחות שנכנסים למאפייה שלכם בוחרים בעוגיות מקרון.

עכשיו, נניח שאתם סקרנים לגבי מספר הלקוחות מתוך ה-10 הבאים שיבחרו את עוגיות המקרון החדשות שלכם. סיטואציה זו היא דוגמה קלאסית להתפלגות בינומית, כאשר משתמשים בהתפלגות בינומית עבור שתי תוצאות שלא יכולות להתרחש בו זמנית בכל ניסוי (רכש או לא רכש, עץ או פלי, קיבל 6 בזריקת קוביה או קיבל מספר אחר, הצלחה או כישלון).

בתרחיש העוגיה שלנו:

• כל החלטה של לקוח אם לקנות או לא לקנות את עוגית המקרון היא "ניסוי".
• "הצלחה" מוגדרת כלקוח שבוחר לרכוש עוגיית מקרון.
• הסיכוי להצלחה (p) הוא 20%, ולפיכך הסיכוי לכישלון הוא 80% (1 - p).

עכשיו, בואו נחשב את הסיכוי לתוצאות שונות באמצעות הנוסחה של ההתפלגות הבינומית:

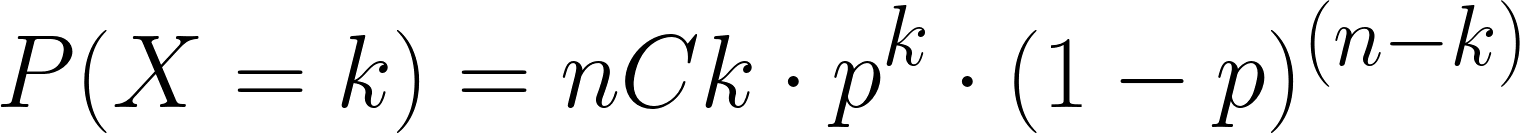
הפרמטרים בנוסחה הם:

• ( n ) הוא מספר הניסויים (לקוחות)
• ( k ) הוא מספר ההצלחות (לקוחות שבחרו לרכוש עוגיות מקרון)
• ( p ) הוא הסיכוי להצלחה
• ( 1-p ) הוא הסיכוי לכישלון

נציב לתוך הנוסחה את הערכים מתוך הבעיה שמעסיקה אותנו:

• n = 10 ניסויים (לקוחות)
• k יכול להיות כל מספר בין 0 ל-10 (0 לקוחות שבחרו, 1 לקוח שבחר, ..., 10 לקוחות שבחרו)
• p = 0.2 20% סיכוי להצלחה, כלומר לקוח שבוחר עוגית מקרון. מה שאומר 80% סיכוי לכישלון, כלומר לקוח שלא בוחר עוגית מקרון.

תיכף ננסה להבין את הנוסחה אבל קודם נברר האם המקרה של עוגיות המקרון מתאים לשימוש בהתפלגות הבינומית.

התנאים לשימוש בהתפלגות בינומית הם:

• יש 2 תוצאות אפשריות בכל ניסוי: הצלחה או כישלון
• הסיכוי p להצלחה הוא זהה בכל הניסויים
• מספר הניסויים n הוא קבוע
• הניסויים עצמאיים ואינם תלויים אחד בשני

ולפיכך נראה שההתפלגות יכולה לשמש אותנו במקרה שלנו.

השאלה הראשונה שמעניינת אותנו היא מה ההסתברות שכל 10 הקונים הבאים ירכשו עוגיות מקרון?

זה קל. כי מה הסיכוי שאחד ירכוש (0.2) וכדי לחשב את הסיכוי ש-10 מאורעות של הצלחה יקרו ברצף צריך להעלות את הסיכוי בחזקת 10:

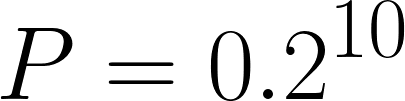
אפשר גם להציב בנוסחה:

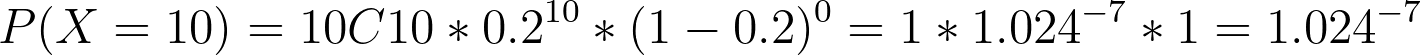
השאלה השנייה שמעניינת אותנו היא מה ההסתברות שאף לא אחד מ-10 קונים ירכוש עוגית מקרון?

אם הסיכוי לרכישה בודדת הוא 0.2 אז הסיכוי לאי רכישה הוא 0.8, וכדי לחשב את ההסתברות להתרחשות 10 מאורעות ברצף נעלה את ההסתברות לאי רכישה בחזקת 10:

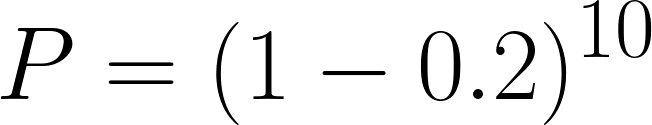
החישוב מאוד פשוט, וגם הצבה בנוסחה תיתן את אותה התוצאה:

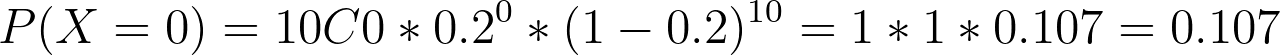
השאלה השלישית היא כבר יותר מעניינת. מה הסיכוי שבדיוק 3 קונים מתוך 10 ירכשו עוגית מקרון?

אולי זה הסיכוי ש-3 ירכשו, ואם הסיכוי שאחד ירכוש הוא 0.2, אז הסיכוי לשלושה מאורעות ברצף הוא 0.2 בחזקת 3, וגם הסיכוי שיתר 7 המאורעות יהיו של אי רכישה מה שאומר שצריך להעלות את 0.8 בחזקת 7:

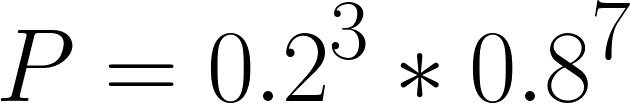
הבעיה היא שחישוב זה לא לוקח בחשבון את כל הקומבינציות. כי יכול שהראשון השני והשלישי ירכשו, אבל גם שהשני, הרביעי והחמישי, ויש עוד הרבה שילובים. כמה שילובים? בוא נחשב:

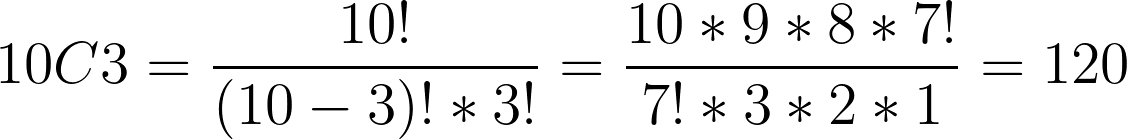
• בסך הכול 120 קומבינציות בהם צריך להתחשב (הנוסחה לעיל מחשבת את מספר הקומבינציות וכדי להבין אותה אתה מוזמן לקרוא את המדריך על תמורות ושילובים בתורת הצירופים).

בשביל לקחת בחשבון את כל הצירופים נכפיל במספר הקומבינציות, כפי שאכן עושה הנוסחה לחישוב ההסתברות הבינומית:

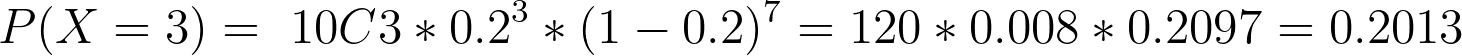
• ההסתברות ל-3 רוכשים מתוך 10 היא 0.2013

במקום לחשב ידנית אפשר להעזר בפונקציה של ספריית scipy של פייתון ששמה stats.binom. באמצעות הפונקציה נחשב את ערך ה-pmf של ההתפלגות הבינומית עבור הפרמטרים:

n - מספר הניסויים
p - הסתברות ההצלחה
k - מספר ההצלחות

# Calculate the probability mass function (PMF) for k, number of successes
pmf_values = binom.pmf(k, n, p)

נחשב באמצעות הצבת ערך הפרמטרים בפונקציה לעיל:

# Parameters for the binomial distribution
n = 10  # Number of trials
p = 0.2  # Probability of success
k = 3 # Number of successes


# Calculate the probability mass function (PMF) for k, number of successes
pmf_values = binom.pmf(k, n, p)

התוצאה:

0.20132659199999992

אפשר להסתכל על גרף ההתפלגות הבינומית כדי לראות את התוצאה:

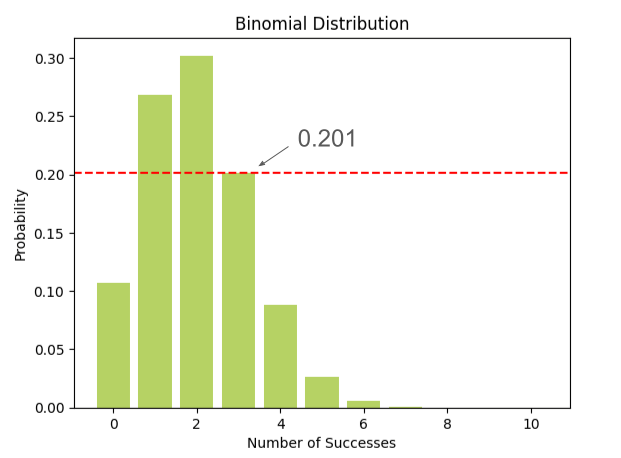
• הגרף מראה את ההסתברות לכל אחת מאפשרויות הרכישה (0 מ-10, 1 מ-10, 2 וכיו"ב). כאשר אפשרויות הרכישה ממוקמות על ציר ה-x וההסתברויות התואמות מיוצגות על ציר ה-y.
• החץ מצביע על רכישה של 3 ומראה שההסתברות היא קצת יותר מ-0.2
• אבל אפשר לראות גם שההסתברות ל-0 רוכשים היא קצת יותר מ-0.1 וגם שההסתברות ל-10 רוכשים היא כל כך נמוכה שלא רואים.

עוד דבר שאפשר ללמוד מהגרף היא למה הכוונה כשאנחנו אומרים pmf* כשמושג זה מתאר את הסתברות של כל אחת מהאפשרויות המתוארת על ידי אחת העמודות (0 רכישות, רכישה 1…10 רכישות עד אינסוף). כאשר סכום ההסתברויות עבור כל האפשרויות (המיוצגות על ידי עמודות) שווה 1.

PMF = Probability Mass Function

נראה שאלות נוספות.

מה הסיכוי שלכל היותר 3 קונים מתוך 10 הבאים ירכשו עוגיות מקרון?

אפשר לחשב את ההסתברות ל-0 רכישות, לרכישה 1, ל-2 ול-3, ואז לסכום את ההסתברויות.

אבל אפשר בדרך יותר פשוטה להשתמש בפונקציה cdf (Cumulative Distribution Function) לחישוב ההסתברויות המצטברות:

# Parameters for the binomial distribution
n = 10  # Number of trials
p = 0.2  # Probability of success

# Calculate the probability of buying at least 3 Macaroon cookies
prob_at_most_3 = binom.cdf(3, n, p)

print(f"The probability of buying at most 3 is: {prob_at_most_3:.4f}")

התוצאה:

The probability of buying at most 3 is: 0.8791

אפשר להסתכל על ההתפלגות הבינומית, ולהגיע לאותה מסקנה:

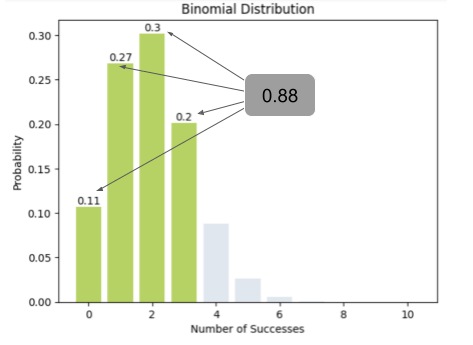
נקנח בשאלה מה הסיכוי שלפחות 3 קונים מתוך 10 הבאים ירכשו עוגיות מקרון?

אפשר לחשב את סכום ההסתברויות של 3 קונים, 4 קונים, 5 קונים, עד אינסוף. אבל דרך קלה יותר היא להתחשב בעובדה שסכום ההסתברויות הוא 1. אז מה שאנחנו יכולים לעשות הוא להפחית מ-1 את ההסתברויות שלא מעניינות אותנו (ההסתברויות לרכישת 2, 1, ו-0 עוגיות). גם במקרה זה נשתמש בפונקציה cdf לחישוב ההסתברות המצטברת של 0 עד 2 רכישות, רק שאח"כ נפחית את הערך המחושב מ-1:

# Parameters for the binomial distribution
n = 10  # Number of trials
p = 0.2  # Probability of success

# Calculate the probability of buying at least 3 Macaroon cookies
prob_at_least_3 = 1 - binom.cdf(2, n, p)

print(f"The probability of buying at least 3 is: {prob_at_least_3:.4f}")

התוצאה:

The probability of buying at least 3 is: 0.3222

ניתן להגיע לאותה מסקנה מהסתכלות בהתפלגות:

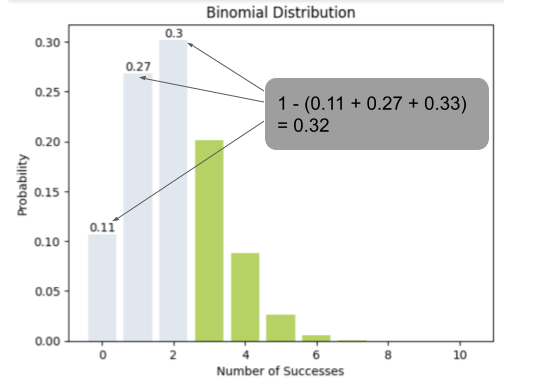
תכונות נוספות של ההתפלגות הבינומית

תוחלת

חישוב תוחלת ההתפלגות הבינומית הוא פשוט מאוד:

E(X) = np

לדוגמה, התוחלת עבור 10 הצלחות כאשר ידוע שהסתברות ההצלחה היא 0.2 היא:

n = 10
p = 0.2
E(x) = np = 10*0.2 = 2

• התוחלת היא 2. וזה גם הגיוני כי אם יש 10 מאורעות וההסתברות להצלחה בכל אחד מהם הוא 0.2 אז תוחלת ההצלחה היא 2. אם נחזור לדוגמה שלנו, אם ההסתברות לרכישה הוא 0.2 אז מתוך 10 רוכשים פוטנציאליים נצפה ש-2 יקנו.

שונות

את השונות נחשב באמצעות הנוסחה:

V(x) = np(1-p)

נחשב את השונות עבור הדוגמה שלנו:

V(x) = 10*0.2*0.8 = 1.6

• מהשונות ניתן להוציא שורש בשביל לחשב את סטיית התקן.

נשתמש ב-numpy כדי לעשות את החישובים:

import numpy as np
from scipy.stats import binom

# Parameters for the binomial distribution
n = 10  # Number of trials
p = 0.2  # Probability of success

# Calculate the expected number (mean)
mean = n * p

# Calculate the variance
v = n * p * (1 - p)


# Calculate the standard deviation
std_dev = np.sqrt(v)

print(f"The expected number (mean) is: {mean:.2f}")
print(f"The variance is: {v:.2f}")
print(f"The standard deviation is: {std_dev:.2f}")

התוצאה:

The expected number (mean) is: 2.00
The variance is: 1.60
The standard deviation is: 1.26

במקום סיכום

מדריכים נוספים שעשויים לעניין אותך

תמורות ושילובים בתורת הצירופים

איך למצוא את מספר הדוגמאות הדרושות ללמידת מכונה?

מבחנים סטטיסטיים עבור בדיקת A/B באמצעות פייתון

מבחן ANOVA - האם ממוצעי קבוצות שונים סטטיסטית

לכל המדריכים בנושא של למידת מכונה

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים