מדריך מעשי על התפלגות פואסונית באמצעות קוד פייתון וציפורים נודדות

התחביב שלך הוא לספור את מספר ציפורי הנחליאלי שנוחתות על עץ הארז בחצר שלך מדי בוקר שבת בין 9:00 ל-10:00 בבוקר. לאחר כמה עשרות שבתות בהם התמדת לתצפת על העץ ועל ניהול רשימות הגעת למסקנה שבשעת המדידה בבקרים של יום שבת נוחתות על העץ בממוצע 3 ציפורי נחליאלי.

מצב זה עשוי לשמש דוגמה להתפלגות פואסונית (Poisson) בה משתמשים כדי להעריך את הסיכויים להתרחשות אירועים בלתי תלויים אשר קורים בקצב קבוע.

במקרה שלנו, המאורע שמעניין אותנו הוא נחיתת נחליאלי על העץ. ממוצע מספר הנחליאלים שנוחתים על העץ הינו 3. מעניין אותנו לדעת מה הסיכוי ל-5 נחיתות נחליאלי על העץ בשעה.

בשביל לחשב את הסיכוי נשתמש בנוסחת ההתפלגות הפואסונית:

$$P(X=x) = \frac{e^{-\lambda}\lambda^{x}}{x!}$$

• λ - (קוראים את זה: למדא) היא ממוצע ההתפלגות הפואסונית (במקרה שלנו, 3).
• x - הוא מספר האירועים שאת הסיכוי להם אנחנו מעוניינים לחשב (במקרה שלנו, 5).
• e - הוא מספר אי-רציונלי (בערך 2.718) הוא משמש בסיס ללוגריתמים הטבעיים ומופיע בתופעות מתמטיות ומדעיות רבות.
• x! - מציין עצרת. לדוגמה, עצרת של 3 היא 3*2*1

נציב את הערכים עבור המקרה שלנו בנוסחה לחישוב ההסתברות הפואסונית:

$$\begin{align*} \lambda &= 3 \\ x &= 5 \end{align*}$$

ונקבל את התוצאה:

$$\begin{align*} P(X=3) &= \frac{e^{-3}*3^{5}}{5!} = 0.100 \end{align*}$$

• ההסתברות ל-5 ציפורים על העץ בשבת בבוקר היא 0.1.

במקום לחשב ידנית אפשר להעזר בפונקציה של ספריית scipy של פייתון ששמה stats.poisson. באמצעות הפונקציה נחשב את ערך ה-pmf של ההתפלגות הבינומית עבור הפרמטרים:

from scipy.stats import poisson


# Define lambda value
lambda_val = 3


# Number of birds to calculate probability for
x = 5


# Calculate probability using Poisson PMF
probability = poisson.pmf(x, lambda_val)


print(f"The probability of observing {x} birds on the tree in an hour with lambda = {lambda_val} is approximately {probability:.2f}.")

התוצאה:

The probability of observing {x} birds on the tree in an hour with lambda = 3 is approximately 0.10

המושג pmf מתאר את הסתברות של כל אחת מהאפשרויות (במקרה שלנו, 0 ציפורים, ציפור 1…10 ציפורים עד אינסוף). כאשר סכום ההסתברויות עבור כל האפשרויות שווה 1.

לצורך המחשת התוצאה נשתמש בקוד פייתון לתיאור התפלגות פואסונית כאשר λ=3. לערך הבדיד המבוקש x=5 נייחד צבע שונה:

# Define lambda value
lambda_val = 3

# Generate x values for probabilities
x = np.arange(0, 15)

# Create Poisson distribution object
dist = poisson(lambda_val)

# Calculate probabilities for each x value
probabilities = dist.pmf(x)

# Highlight the probability of 5 birds
plt.bar(x, probabilities, color='#d5dee9')  
plt.bar(5, probabilities[5], color='#97c022', label='Probability of 5 birds')

# Customize plot appearance
plt.xlabel('Number of Birds on Tree')
plt.ylabel('Probability')
plt.title(f'Poisson Distribution (λ = {lambda_val}) with Probability of 5 Birds Highlighted')
plt.xticks(x)
plt.legend()
plt.show()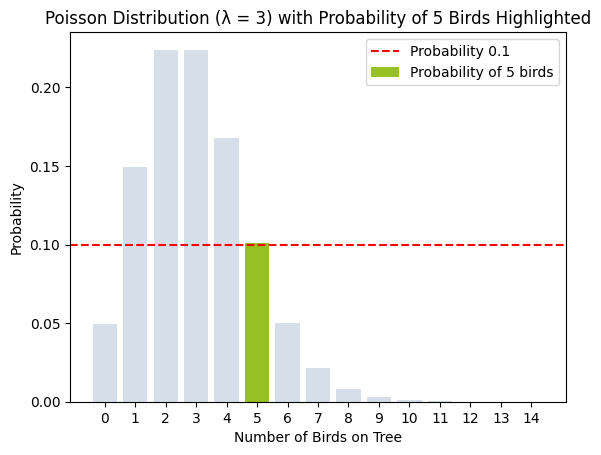

כמו תמיד עם הסתברויות, חשוב לדעת שהמקרה אכן מתנהג בהתאם לרצוי. את ההערכה צריך לעשות לפני שעושים את החישובים אבל פה אנחנו בשביל ללמוד.

התנאים לשימוש בהתפלגות פואסונית הם:

• התפלגות פואסונית היא בדידה מה שאומר שניתן להשתמש בה רק על אירועים שניתן לספור.
• האירועים חייבים להיות בלתי תלויים זה בזה מה שאומר שהתרחשות האחד אסור שתשפיע על התרחשות האחרים.
• האירועים צריכים להתרחש בקצב קבוע.

במקרה שלנו, מספר הציפורים הינו בדיד, אולם ישנם מינים של ציפורים החיים בלהקות כך שנוכחות של ציפור אחת על העץ סביר שתגרור הופעת ציפורים נוספות מהלהקה, וגם לא בטוח שקצב ההתרחשות הוא קבוע בפרט אם מביאים בחשבון שנחליאלי אינו מין אנדמי ועל כן מופיע בארץ בעיקר בעונת הסתיו. כך שההנחה שאירוע הנחיתה של הנחליאלי על העץ מתאימה להתפלגות פואסונית אינה סבירה.

בוא נראה עוד כמה דוגמאות שימצקו אצלנו את ההבנה לגבי אילו נתונים עשויים להתפלג פואסונית:

• משקל הדגים אשר הדייג מיכה מעלה ברשת.
• כמות שבבי השוקולד בכל עוגייה.
• מספר הביקורות החיוביות בגוגל אשר מקבל אתר אינטרנט בחודש.

הדוגמה הראשונה, של משקל הדגים העולים ברשת, אינה מתאימה להתפלגות פואסונית מכיוון שמשקל הוא משתנה רציף. משתנה רציף הוא משתנה שיכול לקבל כל ערך ממשי, בעוד שמשתנה בדיד יכול לקבל רק מספרים שלמים מוגדרים מראש.

הדוגמה השנייה, של כמות שבבי השוקולד בכל עוגייה, עשויה להתאים להתפלגות פואסונית אם יש סיבה להניח שהשבבים עוררבו היטב לתוך הבצק כך שהם לא נדבקו אחד בשני. אם התנאים הללו מתקיימים, אז מספר השבבים בכל עוגייה עשוי להיות משתנה בדיד המתפלג פואסונית.

הדוגמה השלישית, של מספר הביקורות החיוביות שמקבל אתר בחודש, גם היא מתאימה להתפלגות פואסונית אם יש סיבה להניח שאין תלות בין הביקורות והאירועים מתרחשים פחות או יותר בקצב קבוע. אם התנאים הללו מתקיימים, אז מספר הביקורות החיוביות בחודש הוא משתנה בדיד המתפלג פואסונית.

מידע נוסף אותו יש להביא בחשבון הוא שלרוב, משתמשים בהתפלגות הפואסונית על אירועים נדירים יחסית.

דוגמאות נוספות למידע שעשוי להתפלג פואסונית הוא:

• מספר המכוניות ברמזור אדום בשבוע.
• מספר רוכשים בחנות מדי יום.
• מספר הצעדים שצועד אדם ביום.
• כמות הכניסות לדף אינטרנט ביממה.
• מספר ההתפרקויות הרדיו אקטיביות של יסוד פעיל בשנייה.

תכונות נוספות של התפלגות פואסונית

התוחלת, הממוצע והשונות של התפלגות פואסונית שווים לפרמטר λ.

$$E(x) = mean = var = \lambda$$

בשביל לפתח אינטואיציה לגבי אופן התפלגות הנתונים ניעזר בקוד פייתון כדי להציג את מראה ההתפלגות הפואסונית עבור ערכים שונים של λ:

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson


# Lambda values for which to visualize distributions
lambda_values = [1, 2, 5, 10]


# Generate x values for probabilities
x = np.arange(0, 20)


# Create a figure and subplots in a 2x2 grid
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(10, 8))


# Plot each distribution in its respective subplot
for i, lambda_val in enumerate(lambda_values):
   row = i // 2 # Determine row index
   col = i % 2  # Determine column index


   dist = poisson(lambda_val)
   axes[row, col].bar(x, dist.pmf(x), color='#97c022', label=f'λ = {lambda_val}')
   axes[row, col].set_xlabel('Number of Events (x)')
   axes[row, col].set_ylabel('Probability')
   axes[row, col].set_title(f'Poisson Distribution with λ = {lambda_val}')
   axes[row, col].legend()


plt.tight_layout()  # Adjust spacing between subplots
plt.show()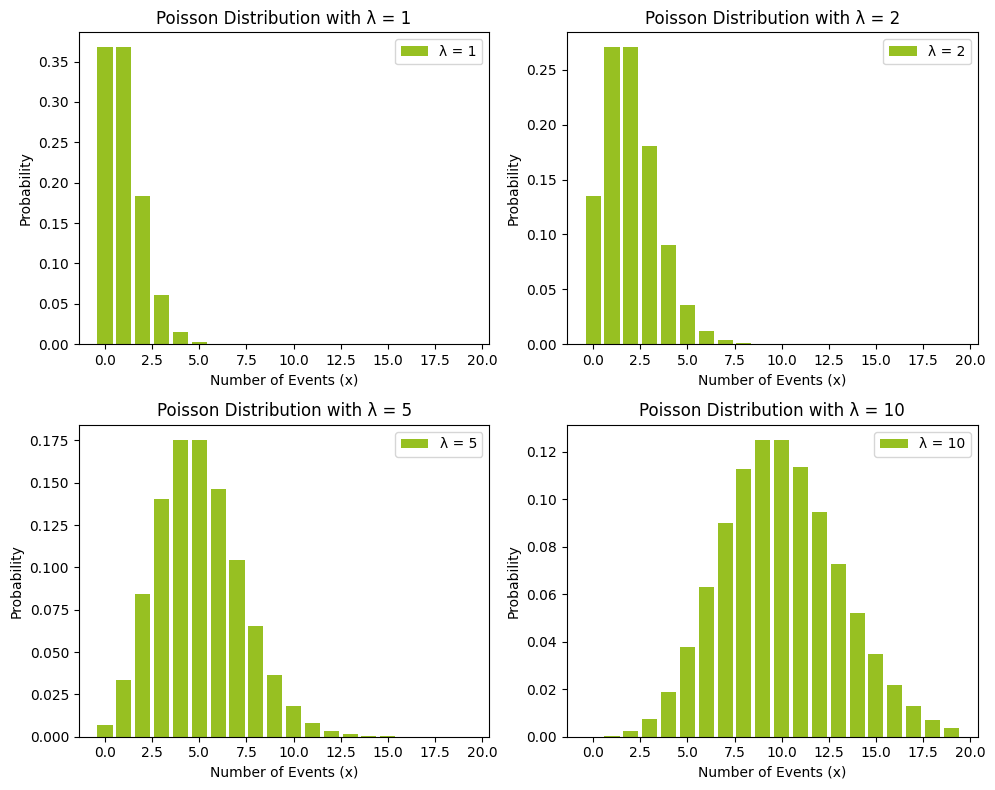

צריך לשים לב ש:

• ככל שהערך של λ עולה כך ההתפלגות הופכת לסימטרית יותר.
• שיאה של ההסתברות מוטה לימין ככל שהערך של λ גדל.
• ככל ש-λ גדול יותר כך גדלה גם השונות. מה שלא אמור להפתיע כיוון שהשונות שווה λ.

עוד דבר שאפשר ללמוד מהגרף היא למה הכוונה כשאנחנו אומרים pmf כשמושג זה מתאר את הסתברות של כל אחת מהאפשרויות המתוארת על ידי אחת העמודות (0 ציפורים, ציפור 1 על העץ…2…10 עד אינסוף ציפורים). כאשר סכום ההסתברויות עבור כל האפשרויות (כאשר כל אפשרות מיוצגת על ידי אחת העמודות) שווה 1.

עוד 2 בעיות רגע לפני שכל אחד עף לדרכו

מה הסיכוי שלכל היותר 3 ציפורים ינחתו על העץ בשעה?

אפשר לחשב את ההסתברות ל-0 ציפורים, לציפור 1, ל-2 ול-3, ואז לסכום את ההסתברויות.

אבל אפשר בדרך יותר פשוטה להשתמש בפונקציה cdf לחישוב ההסתברויות המצטברות:

# Define lambda value
lambda_val = 3


# Calculate the probability of at least 3 birds on a tree
prob_at_most_3 = poisson.cdf(3, lambda_val)


print(f"The probability of at most 3 birds on a tree is: {prob_at_most_3:.2f}")

התוצאה:

The probability of at most 3 birds on a tree is: 0.65

האם התוצאה נכונה? אפשר להסתכל על ההתפלגות הפואסונית כדי לאשש את התוצאה:

# Parameters for the Poisson distribution
lambda_val = 3


# Generate x values
x = range(0, 15)


# Create Poisson distribution object
dist = poisson(lambda_val)


# Calculate probabilities for each x value
probabilities = dist.pmf(x)  # Calculate probabilities using pmf


colors = ['#97c022' if i <= 3 else '#d5dee9' for i in x]


# Annotate each bar with its y-axis value
for i, value in enumerate(probabilities):  # Iterate over probabilities
   if i <= 3:
       plt.text(i, value, f'{value:.2f}', ha='center', va='bottom')


# Plot the Poisson distribution
plt.bar(x, probabilities, align='center', color=colors, alpha=0.7)  # Use probabilities for y-axis


plt.xlabel('Number of Birds on Tree')
plt.ylabel('Probability')
plt.title(f'Poisson Distribution (λ = {lambda_val}) for at most 3 birds on a tree')
plt.show()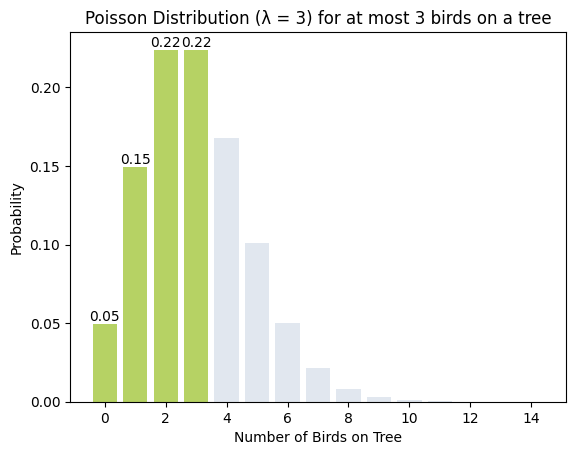

• סכום העמודות הירוקות המסמלות 3 ציפורים או פחות הוא אכן 0.65 בקירוב של נקודה עשרונית.
• עוד דבר שאנחנו יכולים ללמוד מהתרשים הוא מהו CDF (שזה ראשי תיבות של Cumulative Distribution Function) וממנה אנחנו יכולים ללמוד את הצטברות הסיכויים עד לנקודה מסוימת. במקרה שלנו, הצטברות הסיכויים לעד 3 ציפורים על העץ.

בעיה נוספת היא מה הסיכוי שלפחות 3 ציפורים ינחתו על העץ בשעה?

אפשר לחשב את סכום ההסתברויות של 3 ציפורים, 4 ציפורים, 5 ציפורים, 6 ציפורים, …, עד אינסוף. אבל דרך קלה יותר היא להתחשב בעובדה שסכום ההסתברויות הוא 1. אז מה שאנחנו יכולים לעשות הוא להפחית מ-1 את ההסתברויות שלא מעניינות אותנו (ההסתברויות של 2, 1, ו-0 ציפורים). גם במקרה זה נשתמש בפונקציה cdf לחישוב ההסתברות המצטברת של 0 עד 3 ציפורים, וגם נפחית את הערך המחושב מ-1.

את חישוב ההסתברות לכך שלפחות 3 ציפורים ינחתו על העץ נפתור בשני שלבים:

1. חישוב ההסתברות המצטברת של 0 עד 2 ציפורים באמצעות הפונקציה poisson.cdf.
2. הפחתת הערך המחושב מ-1.

הקוד הבא יחשב את ההסתברות:

# Define lambda value
lambda_val = 3


# Calculate the probability of at least 3 birds on a tree
prob_at_least_3 = 1 - poisson.cdf(2, lambda_val)


print(f"The probability of at least 3 birds on a tree is: {prob_at_least_3:.2f}")

התוצאה:

The probability of at least 3 birds on a tree is: 0.58

אפשר להגיע לאותה התוצאה מהסתכלות על הגרף של ההתפלגות הפואסונית עבור λ=3:

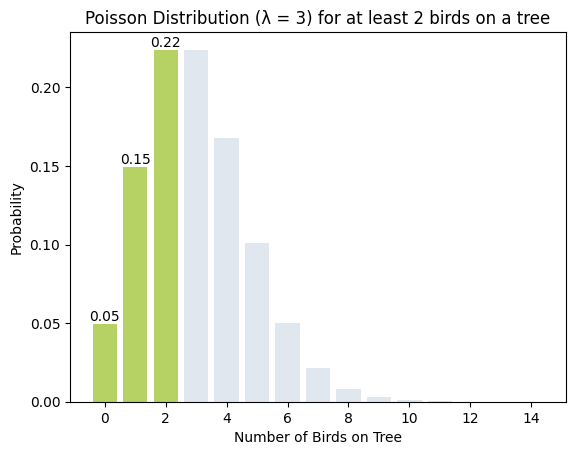
סכום ההסתברויות של העמודות שצבעם ירוק המסמלות 0 - 2 ציפורים הוא :

$$P(x<=2) = 0.05 + 0.15 + 0.22 = 0.42$$

נפחית את הערך המחושב מ-1 וכך נגיע ל-0.58 מה שיאשר את החישוב שעשינו באמצעות הפונקציה poisson.cdf של פייתון.

מדריכים נוספים שעשויים לעניין אותך

התפלגות בינומית - הלכה למעשה

תמורות ושילובים בתורת הצירופים

מה זה A/B testing - בדיקת A/B?

לכל המדריכים בנושא של למידת מכונה

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים