להבין את פונקציות ההסתברות: PMF, CDF, PDF
PMF, CDF, ו-PDF הן פונקציות הסתברות שכל מי שמתעניין בסטטיסטיקה והסתברות חייב להכיר. במדריך זה נפרט מה עושה כל אחת מהפונקציות, מה מבדיל ביניהן ומה כל אחת מהן תורמת לניתוח נתונים.
1. Probability Mass Function (PMF)
פונקציית ה-PMF (Probability Mass Function) משמשת עבור משתנים בדידים, ומלמדת מה הסיכוי לקבל ערך בדיד מסויים.
- דוגמה: מה ההסתברות לקבלת "3" בהטלת קובייה הוגנת? התשובה אותה תספק פונקציית ה-PMF היא 1/6.
- תיאור גרפי: הפונקציה מתוארת באמצעות תרשים עמודות, בו כל עמודה מייצגת את ההסתברות לתוצאה מסוימת.
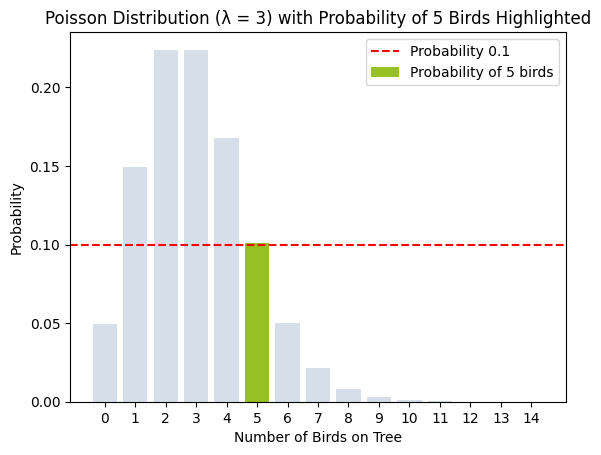
* סך כל ההסתברויות שמספקת פונקצית ה-PMF שווה ל-1.
2. Cumulative Distribution Function (CDF)
פונקציית CDF (Cumulative Distribution Function) מתאימה למשתנים בדידים ורציפים. במקום להציג הסתברות לערך יחיד, ה-CDF מחשבת את ההסתברות לקבלת ערך שווה או נמוך מערך נתון, כלומר הסיכוי הכולל עד לנקודה זו.
- דוגמה: מה הסיכוי לעד 5 רכישות ביום בחנות מסוימת?
- תיאור גרפי: קו שמתחיל ב-0 ועולה באופן מונוטוני ל-1, כשהוא מציין את ההסתברויות המצטברות עד לערך המקסימלי.
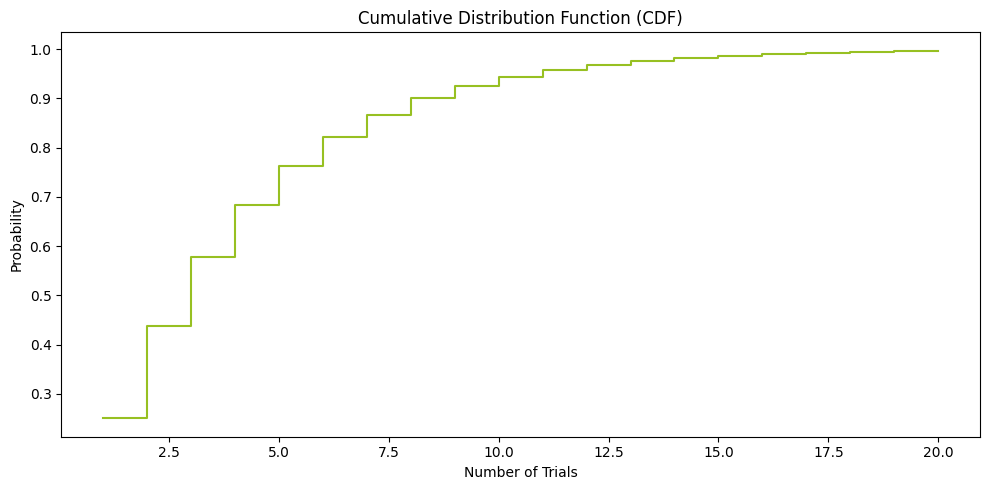
3. Probability Density Function (PDF)
פונקציית PDF (Probability Density Function) משמשת עבור משתנים רציפים, ומייצגת את ההסתברות עבור טווח ערכים נתון. בפונקציה זו איננו מקבלים הסתברות עבור ערך יחיד אלא עבור תחום מסוים כיוון שהפונקציה עובדת עם משתנה רציף ולא בדיד.
- דוגמה: מה ההסתברות שגובהו של גבר בוגר יהיה בין 165 ל-185 ס"מ?
- תיאור גרפי: עקומה, כאשר השטח מתחת לעקומה בין שתי נקודות מייצג את ההסתברות להימצאות המשתנה בטווח המסוים.
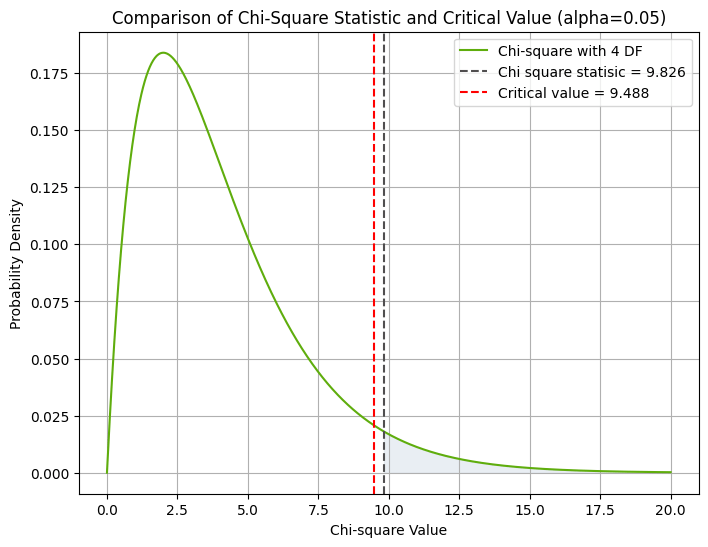
סיכום הפונקציות
- פונקציית PMF עונה לשאלה "מה ההסתברות לתוצאה מסוימת?" והיא מיועדת לערכים בדידים.
- פונקציית CDF עוזרת לקבוע "מה ההסתברות להגיע עד (כולל) ערך מסוים?", ומשמשת להסתברויות בדידות ורציפות כאחד.
- פונקציית PDF מיועדת להסתברויות רציפות, ועוזרת לענות על השאלה "מה ההסתברות להיות בטווח הזה?".
הטבלה הבאה מסכמת את 3 פונקציות ההסתברות:
| פונקציה | ר"ת | הסבר | סוג התפלגות | הצגה גרפית | דוגמה |
|---|---|---|---|---|---|
| PMF | Probability Mass Function | הסתברות של תוצאה בדידה | בדידה | תרשים עמודות שבו כל עמודה מציגה את ההסתברות לאירוע מסוים | ההסתברות ל-2 רכישות בדיוק |
| CDF | Cumulative Distribution Function | הסתברות ל-X אירועים או פחות | רציפה או בדידה | גרף שמתחיל ב-0 ועולה מונוטונית עד שמגיע ל-1 | ההסתברות לכל היותר 5 רכישות |
| Probability Density Function | הסתברות של טווח ערכים רציף | רציפה | עקומה עם שטח מתחת לעקומה המציין הסתברות | הסתברות לגובה בין 165 ל-185 עבור גבר בוגר |
הבנת פונקציות ההסתברות במדריך עוזרת לפרש את הנתונים בצורה טובה יותר, להבין תופעות בעולם האמיתי ולקבל החלטות על בסיס תובנות סטטיסטיות.
מדריכים נוספים בסדרה על למידת מכונה שעשויים לעניין אותך
מדריך הסתברות מעריכית (אקספוננציאלית) מהלכה למעשה עם פייתון
לכל המדריכים בנושא של למידת מכונה
אהבתם? לא אהבתם? דרגו!
0 הצבעות, ממוצע 0 מתוך 5 כוכבים


המדריכים באתר עוסקים בנושאי תכנות ופיתוח אישי. הקוד שמוצג משמש להדגמה ולצרכי לימוד. התוכן והקוד המוצגים באתר נבדקו בקפידה ונמצאו תקינים. אבל ייתכן ששימוש במערכות שונות, דוגמת דפדפן או מערכת הפעלה שונה ולאור השינויים הטכנולוגיים התכופים בעולם שבו אנו חיים יגרום לתוצאות שונות מהמצופה. בכל מקרה, אין בעל האתר נושא באחריות לכל שיבוש או שימוש לא אחראי בתכנים הלימודיים באתר.
למרות האמור לעיל, ומתוך רצון טוב, אם נתקלת בקשיים ביישום הקוד באתר מפאת מה שנראה לך כשגיאה או כחוסר עקביות נא להשאיר תגובה עם פירוט הבעיה באזור התגובות בתחתית המדריכים. זה יכול לעזור למשתמשים אחרים שנתקלו באותה בעיה ואם אני רואה שהבעיה עקרונית אני עשוי לערוך התאמה במדריך או להסיר אותו כדי להימנע מהטעיית הציבור.
שימו לב! הסקריפטים במדריכים מיועדים למטרות לימוד בלבד. כשאתם עובדים על הפרויקטים שלכם אתם צריכים להשתמש בספריות וסביבות פיתוח מוכחות, מהירות ובטוחות.
המשתמש באתר צריך להיות מודע לכך שאם וכאשר הוא מפתח קוד בשביל פרויקט הוא חייב לשים לב ולהשתמש בסביבת הפיתוח המתאימה ביותר, הבטוחה ביותר, היעילה ביותר וכמובן שהוא צריך לבדוק את הקוד בהיבטים של יעילות ואבטחה. מי אמר שלהיות מפתח זו עבודה קלה ?
השימוש שלך באתר מהווה ראייה להסכמתך עם הכללים והתקנות שנוסחו בהסכם תנאי השימוש.