SVD - Singular Value Decomposition באמצעות פייתון

באלגברה לינארית, SVD מפרק מטריצה, גם אם אינה ריבועית, לשלוש מטריצות. הפירוק חושף תובנות מעניינות אודות טרנספומציה של מטריצות ויש לו שימושים מועילים בלמידת מכונה. במדריך זה נראה איך לבצע SVD בפייתון וכיצד להשתמש בהליך לדחיסת מידע.

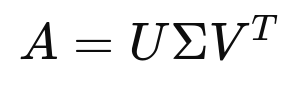
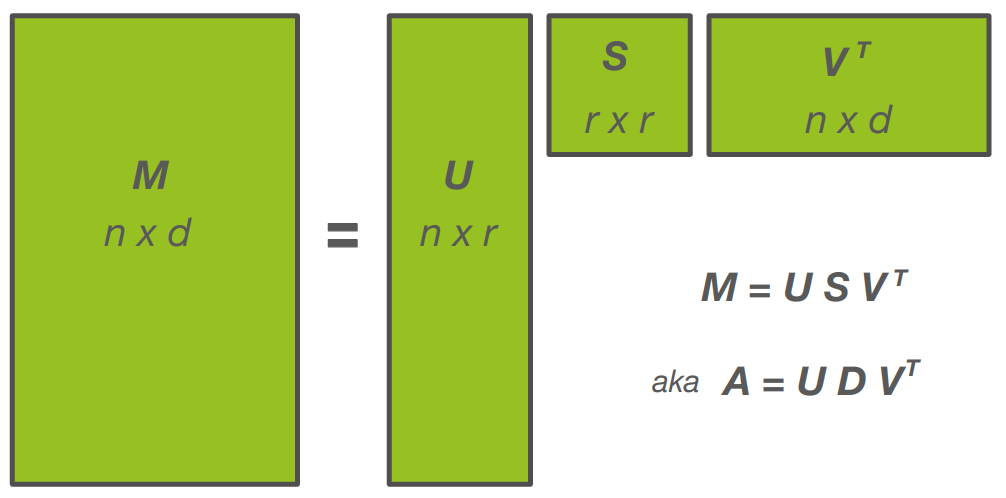
אלגוריתם SVD מפרק את המטריצה M לשלוש מטריצות: U ו-V הם אורתונורמליות ו-S דיאגונלי.

איך לעשות SVD באמצעות פייתון?

את המטריצה M נפרק ל-3 המטריצות באמצעות הפונקציה linalg.svd של ספריית Numpy:

import numpy as np

M = np.array([[-1, 2], [3, -2], [5, 7]])

U, S, V = np.linalg.svd(M)

תוצאת הפירוק תהיה 3 מטריצות:

• U היא מטריצה אורתוגונלית אשר העמודות שלה הם הוקטורים הסינגולריים השמאליים של המטריצה המקורית.

• S היא מטריצה דיאגונלית הפריטים לאורך האלכסון הראשי שלה הם הערכים הסינגולריים של מטריצת המקור.

• V היא מטריצה אורתוגונלית ריבועית כאשר העמודות שלה הם הוקטורים הסינגולריים הימניים.

כדי לבחון שהפירוק הצליח ננסה להרכיב את מחדש את המטריצה המקורית מ-3 המטריצות. לשם כך:

1. ניצור מטריצה דיאגונלית מהערכים הסינגולריים:

   S = np.concatenate((np.diag(S), [[0, 0]]), axis=0)

   • כיוון שדרושה מטריצה דיאגונלית שלה 3 שורות בשביל שניתן יהיה לכפול אבל גובה המטריצה הדיאגונלית הוא 2 בלבד, הוספנו בתחתית שורה של אפסים.

2. כדי להרכיב מחדש את המטריצה המקורית (M) נכפיל את 3 המטריצות לפי סדר:

   np.dot(U, np.dot(S, V))

התוצאה היא המטריצה המקורית לפני הפירוק:

array([[-1.,  2.],
          [ 3., -2.],
          [ 5.,  7.]])

היכולת שלנו לפרק מטריצה לגורמים, ואחר כך לחבר את המטריצה חזרה מהגורמים המרכיבים אותה מוכיחה את נכונות הפירוק שעשינו באמצעות האלגוריתם SVD.

דחיסת מידע באמצעות SVD

SVD הוא טכניקה יעילה באלגברה לינארית אשר מפרקת מטריצה לשלוש מטריצות פשוטות יותר. פירוק זה מאפשר מספר יישומים מעשיים, שאחד מהם הוא דחיסת מידע. במדריך זה נדגים את עוצמת דחיסת המידע באמצעות SVD באמצעות דוגמה של דחיסת תמונה.

נעלה תמונה בשחור לבן אותה נייצג כמטריצה כאשר כל אלמנט במטריצה מתאר את עוצמתו של אחד הפיקסלים:

from PIL import Image
import matplotlib.pyplot as plt
import numpy as np


img = Image.open("my_bw_image.png")
_ = plt.imshow(img)

נמיר את התמונה לשחור-לבן (לכל מקרה שלא יהיה):

# Convert to grayscale to reduce the dimensionality
gray_image = img.convert('LA')
_ = plt.imshow(gray_image)

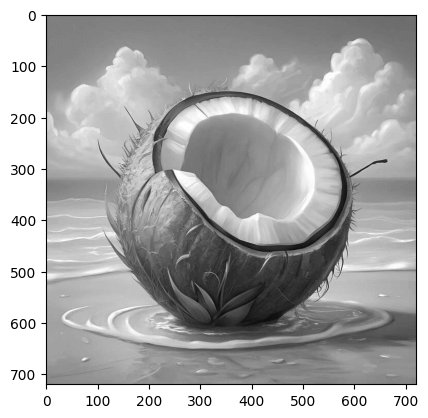
נמיר את התמונה למטריצה:

# Convert the data into a Numpy matrix
matrix_image = np.array(list(gray_image.getdata(band=0)), float)
matrix_image.shape = (gray_image.size[1], gray_image.size[0])
matrix_image = np.matrix(matrix_image)
_ = plt.imshow(matrix_image, cmap='gray')

נפרק את המטריצה באמצעות SVD:

# Calculate the image SVD
U, sigma, V = np.linalg.svd(matrix_image)

האם תוצאת הפירוק היא מה שאנו מצפים לו? נרכיב את התמונה מ-3 המטריצות אליה היא פורקה כדי לראות שאנחנו מקבלים את התמונה המקורית:

# Reconstruct the image
reconstructed_image = np.matrix(U[:, :1]) * np.diag(sigma[:1]) * np.matrix(V[:1, :])
_ = plt.imshow(reconstructed_image, cmap='gray')

התוצאה תואמת את המקור:

נוסיף בהדרגה וקטורים סינגולריים כדי לראות את ההשפעה על איכות התמונה:

for i in [10, 20, 40, 70]:
   reconstructed_image = np.matrix(U[:, :i]) * np.diag(sigma[:i]) * np.matrix(V[:i, :])
   plt.title('{} singular vectors'.format(i))
   plt.show(plt.imshow(reconstructed_image, cmap='gray'))

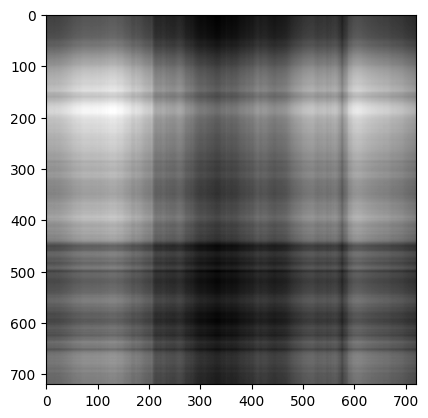
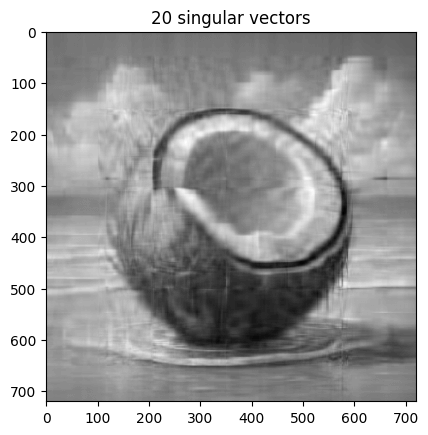
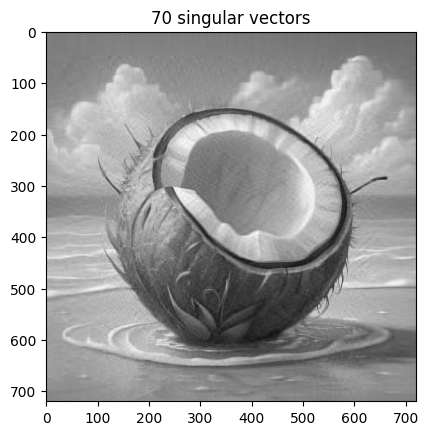
כמה מידע נחסך בתהליך?

את גודל נתוני תמונת הקלט נחשב מהכפלת גובה התמונה בפיקסלים ברוחב:

input = H x W = 720 x 720 = 518,400

את גודל נתוני התמונה לאחר הדחיסה נחשב על פי מספר המימדים בהם השתמשנו לצורך הרכבה מחדש של התמונה:

output = H x 70 + 70 + W x 70 = 720 x 70 + 70 + 720 x 70 = 100,870

נחשב את יחס הדחיסה:

compression_ratio = 100,870/518,400 = 19%

למה להשתמש ב-SVD לדחיסת מידע?

אחת הסיבות העיקריות לכך ש SVD כל כך יעיל לדחיסת נתונים היא יכולתו לסדר את הערכים הסינגולריים באופן המשקף את חשיבותם למבנה הנתונים. הערכים הסינגולריים המתקבלים בתהליך ה-SVD של מטריצה מסודרים על פי גודלם כאשר הערכים הסגוליים הגדולים ביותר מייצגים כיוונים במידע המכילים שונות גבוהה יותר. כיוונים אילה מכילים את התכונות החשובות ביותר של המידע. לעומת זאת, ערכים סינגולריים נמוכים יותר מייצגים כיוונים המכילים פחות שונות, מה שיכול להיות רעש או תכונות פחות מעניינות. על ידי הסרת הערכים הנמוכים והוקטורים שלהם, SVD מצליח לתפוס את ההיבטים החשובים ביותר של המידע. בדרך זו, רוב המידע החשוב נשמר בתהליך תוך הפחתה במספר המימדים ובדרישות למקום בזכרון.

סיכום

באמצעות SVD ניתן הצלחנו להגיע לדחיסה משמעותית של מידע הודות ליכולתו להפריד את החלקים העיקריים מכל היתר. על ידי הפחתת הממדיות של הנתונים, SVD עוזר למתן את קללת הממדיות, שהיא בעיה נפוצה בלמידת מכונה, שבה ביצועי האלגוריתמים יורדים ככל שמספר התכונות בנתונים גדל.

למדריכים נוספים בסדרה על למידת מכונה

12 דברים שאתה חייב לדעת כשאתה עובד עם ספריית Numpy של Python

מציאת יחס הזהב בתוך סדרת מספרים עולה באמצעות (קצת) אלגברה לינארית

מציאת ערכים ווקטורים טיפוסיים של מטריצה עם ובלי פייתון

לכל המדריכים בנושא של למידת מכונה

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים