חיזוי טמפרטורות באמצעות למידת מכונה
חיזוי של סדרות נתונים מציב אתגר גדול בפני למידת מכונה בגלל שהמחשב צריך לזכור את התוצאות שחושבו בשלבים הקודמים של תהליך הלמידה דבר שאינו אפשרי ברשת נוירונית רגילה (feed forward network). כדי לטפל בבעייה ניתן להשתמש בסוג מיוחד של למידת מכונה, RNN - Recurrent Neural Networks.
ישנם יחידות שונות שמהם ניתן להרכיב RNN, ובמדריך זה נלמד ליישם RNN המבוסס על יחידות LSTM (Long Short Term Memory).
רשתות LSTM משתמשות ביחידות (במקום בנוירונים), כשכל יחידה מכילה 3 סוגי שערים:
- שער שכחה, Forget Gate, שמחליט באיזה חלק מהנתונים שהוא מקבל לא להשתמש.
- שער קלט, Input Gate, שמחליט איזה חלק מהמידע שמגיע מהקלט יוזן לתוך הרשת.
- שער פלט, Output Gate, שמחליט איזה מידע להעביר לשכבה הבאה בתור.
כל יחידה מכילה משקלות משלה ובכך היא מהווה מכונה קטנה בתוך המכונה הגדולה.
את יחידות ה- LSTM מסדרים בשכבות.
את הקוד המלא שנפתח במדריך תוכלו להוריד על ידי לחיצה על הקישור
מטרת המדריך
במדריך זה ננסה לחזות את הטמפרטורות לשנים 2016-2018 על פי נתוני הטמפרטורות שנמדדו בין השנים 2004 עד 2015.
מאגר הנתונים
את המידע עבור הטמפרטורות בנמל אשדוד הורדתי מאתר מאגרי המידע הממשלתיים https://data.gov.il והוא כולל מדידות שנערכו מדי יום בין השנים 2004-2019. להורדת קובץ הנתונים לחץ כאן.
סביבת העבודה וייבוא הספריות שמשמשות במדריך
סביבת העבודה שבה פותח הקוד היא Google Colab, הספרייה לעיבוד המידע היא sklearn והספרייה ללמידת מכונה היא TensorFlow.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
from tensorflow.keras.models import Sequential, load_model
from tensorflow.keras.layers import LSTM, Dense, Dropout
import os
טעינת הנתונים
את הנתונים טענתי באמצעות קוד סטנדרטי המשמש לטעינת קבצים בסביבת Google Colab.
from google.colab import files
uploaded = files.upload()import io
df = pd.read_csv(io.BytesIO(uploaded['ims_data.csv']),usecols=['date', 'time', 'temp'])נציץ במסד הנתונים:
df.head()| date | time | temp | |
|---|---|---|---|
| 0 | 01-08-2004 | 02:00 | 25.2 |
| 1 | 01-08-2004 | 05:00 | 24.2 |
| 2 | 01-08-2004 | 08:00 | 27.3 |
| 3 | 01-08-2004 | 11:00 | 31.3 |
| 4 | 01-08-2004 | 14:00 | 29.7 |
הכנת הנתונים ללמידת מכונה
בסט הנתונים שהורדתי היה פורמט התאריך כמקובל בישראל (dd-mm-YYYY) ועל כן כתבתי את הפונקציה הבאה שממירה את הפורמט לזה המקובל בעולם המחשבים:
def to_international_date(d):
date = d.split('-')
day = date[0]
month = date[1]
year = date[2]
return '%s-%s-%s' % (year, month, day)השורות הבאות ממירות את התאריך לפורמט datetime. על ידי צירוף עמודת התאריך עם עמודת השעה ליצירת עמודה ששמה "datetime". בנוסף, מורידות את העמודות המיותרות כדי שנשאר רק עם מה שאנחנו צריכים.
# Convert to the date format
df['date'] = df['date'].apply(to_international_date)
# Convert date and time to datetime
df['datetime'] = pd.to_datetime(df['date'] + ' ' + df['time'])
# Drop columns
df = df.drop(['date', 'time'], axis=1)
# Clean the data
df = df[df['temp'] != '-']את עמודת הטמפרטורה ננקה מערכים חסרים שמסומנים באמצעות קו מפריד "-", ונגדיר את סוג הנתונים לסוג float כי המחשב יודע להתמודד עם מספרים ולא עם מחרוזות שאותם סיפק לנו קובץ מסד הנתונים.
# Clean the temp column
df = df[df['temp'] != '-']
# Set the type of temp to float
df['temp'] = df['temp'].astype(float)נשרטט את עמודת הטמפרטורות כנגד התאריכים:
# Plot and describe the data
plt.plot(df['datetime'], df['temp'])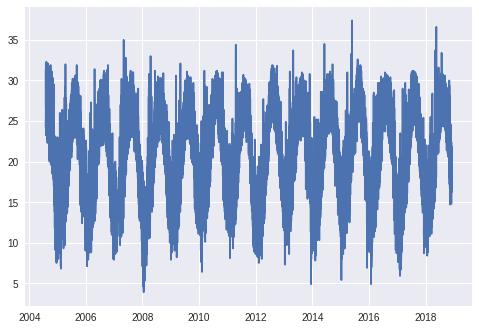
ניתן לראות שינוי מחזורי בטמפרטורות בהתאם לעונות השנה ולשעות ביממה. מכיוון, שאין חריגים אפשר להמשיך לשלבים הבאים בלי צורך להשמיט נתונים.
נגדיר את עמודת datetime בתור האינדקס:
# Set the index
df = df.set_index('datetime')נתאר את מדדי המרכז כדי לבדוק שסט הנתונים סביר:
# Describe
df.describe()| temp | |
|---|---|
| count | 41142.000000 |
| mean | 21.582084 |
| std | 5.498377 |
| min | 3.900000 |
| 25% | 17.300000 |
| 50% | 21.900000 |
| 75% | 26.500000 |
| max | 37.400000 |
נתאר את סט הנתונים גם באמצעות התכונות הבאות:
df.info()
df.shape
DatetimeIndex: 41142 entries, 2004-08-01 02:00:00 to 2018-11-30 23:00:00
Data columns (total 1 columns):
temp 41142 non-null float64
dtypes: float64(1)
memory usage: 642.8 KB
(41142, 1) מערך של 41142 ערכים מסוג float.
נפריד את המידע לשני סטים. סט אימון וסט חיזוי כשהאימון מתבצע מהנתונים שנצברו בין 1.1.2004 ועד 31.12.15, והחיזוי על נתוני השנים 2016-2018.
## Separate between the train and test datasets
split_date = pd.datetime(2015,12,31)
dataset_train = df[:split_date]
dataset_test = df[split_date:]
# Plot the datasets
ax = dataset_train.plot()
dataset_test.plot(ax=ax)
plt.legend(['train','test'])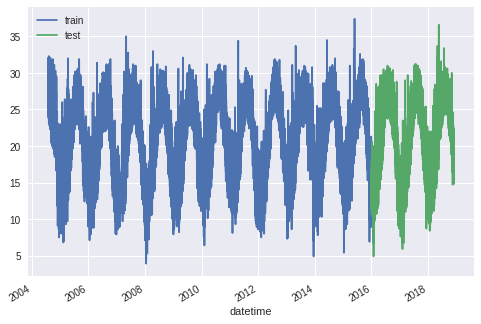
מכיוון שלמידת מכונה רגישה לטווח הערכים נהוג לנרמל את הנתונים לטווח שבין 0 ל-1:
# Scale the datasets
scaler = MinMaxScaler(feature_range=(0,1))
dataset_train_scaled = scaler.fit_transform(dataset_train)
dataset_test_scaled = scaler.transform(dataset_test)
print(dataset_train_scaled[:5]) # The first 5 data points
print(dataset_test_scaled[-5:]) # The last 5 data points[[0.6358209 ] [0.60597015] [0.69850746] [0.81791045] [0.77014925]] [[0.52835821] [0.53432836] [0.51940299] [0.51044776] [0.50746269]]
הדרך לפתור את בעית החיזוי של הטמפרטורות היא באמצעות רגרסיה שמוצאת קשר בין עמודת ה-x וה-y. בלמידת מכונה, הערכים של עמודת ה-x נקראים feature והערכים של עמודת ה -y מכונים labels. ה-features משמשים כדי לחזות את ה-labels.
איך נהפוך מערך של נתונים לסטים של features ו-labels? נשתמש בפונקציה שיוצרת את הסטים.
לדוגמה, את מערך הנתונים הבא:
[1, 2, 3, 4, 5, 6, 7]
הפונקציה תהפוך ל-4 סטים:
| features | label |
|---|---|
| [1, 2, 3] | 4 |
| [2, 3, 4] | 5 |
| [3, 4, 5] | 6 |
| [4, 5, 6] | 7 |
את הפונקציה create_dataset נזין בסדרות של ערכים והיא תפריד מתוכם את ה- features וה-labels כאשר סט של 30 מדידות רצופות ישמש לחיזוי המדידה הבאה. הסט של 30 המדידות יהיה feature והערך הבא בתור יהיה label שאותו אנחנו מנסים לחזות.
# Takes a series of 30 time points as feature and the next point as label
def create_dataset(df):
x = [] # features from the previous 50 time points
y = [] # labels from the current time points
for i in range(30, df.shape[0]):
x.append(df[i-30:i,0])
y.append(df[i,0])
x = np.array(x)
y = np.array(y)
return x,yנפריד את הסטים שישמשו לאימון באמצעות הפונקציה create_dataset:
x_train, y_train = create_dataset(dataset_train_scaled)כמו גם את הסטים שישמשו לחיזוי:
x_test, y_test = create_dataset(dataset_test_scaled)כדי לקבל תחושה לגבי הנתונים נדפיס את הצורה שלהם:
print(x_train.shape)
print(x_test.shape)(32705, 30) (8377, 30)
הצורה היא דו-ממדית. הממד הראשון הוא מספר הדוגמאות, והשני הוא מספר המדידות בסט כפי שהגדרנו בפונקציה create_dataset.
הצורה של הנתונים הדרושה לצורך הזנת תאי LSTM היא של tuple תלת ממדי. לפיכך, נמיר את הנתונים לצורה הדרושה:
# Reshape data for LSTM layer
# Make a 2 dimensional tuple into 3 dimensional
x_train = np.reshape(x_train, (x_train.shape[0], x_train.shape[1], 1))
x_test = np.reshape(x_test, (x_test.shape[0], x_test.shape[1], 1))
print(x_train.shape)
print(x_test.shape)(32705, 30, 1) (8377, 30, 1)
את שני הממדים הראשונים השארנו כפי שהם והוספנו מימד שלישי שערכו 1 בגלל שמערך הנתונים הוא חד-ממדי (uni-variate).
פיתוח המודל המשמש ללמידת מכונה
מודל TensorFlow המשמש ללמידת מכונה הוא מסוג sequential, והוא כולל 3 שכבות:
model = Sequential()
model.add(LSTM(units=48, return_sequences=True, input_shape=(x_train.shape[1], 1)))
model.add(Dropout(0.2))
model.add(LSTM(units=48, return_sequences=True, input_shape=(x_train.shape[1], 1)))
model.add(Dropout(0.2))
model.add(LSTM(units=48))
model.add(Dropout(0.2))
model.add(Dense(units=1))- 2 שכבות LSTM, שבכל אחת 48 תאים.
- הנתונים שיוצאים משכבת ה-LSTM עוברים דרך שכבת dropout שמפחיתה באקראי 20% מהתוצאות כדי למנוע למידת יתר של הדוגמאות וכך להקל על המודל להכליל לדוגמאות שהמודל לא ראה בתהליך האימון.
- השכבה האחרונה היא של רשת נוירונית רגילה Dense שמכילה יחידה אחת בגלל שהבעיה היא בעיית רגרסיה שאנחנו מצפים ממנה לחזות רק את הטמפרטורה.
נסכם את המודל שפתחנו:
model.summary()Layer (type) Output Shape #Param ========================================== lstm_1 (LSTM) (None, 30, 48) 9600 __________________________________________ dropout_1 (Dropout) (None, 30, 48) 0 ___________________________________________ lstm_2 (LSTM) (None, 30, 48) 18624 ___________________________________________ dropout_2 (Dropout) (None, 30, 48) 0 ___________________________________________ lstm_3 (LSTM) (None, 48) 18624 ___________________________________________ dropout_3 (Dropout) (None, 48) 0 ___________________________________________ dense_1 (Dense) (None, 1) 49 =========================================== Total params: 46,897 Trainable params: 46,897 Non-trainable params: 0
נקמפל את המודל:
model.compile(loss='mean_squared_error', optimizer='adam')נגדיר את התנאים שבהם המודל יפסיק לרוץ:
from tensorflow.keras.callbacks import EarlyStopping
es = EarlyStopping(monitor='val_loss',
min_delta=0,
patience=2,
verbose=2,
mode='auto')נריץ את תהליך הלמידה:
model.fit(x_train, y_train, epochs=200, batch_size=32, validation_data=(x_test,y_test), callbacks=[es])
הערכת המודל
לפני שנעריך את איכות התחזית על סט הנתונים test שהמחשב לא ראה, נבדוק את איכות התחזיות עבור המידע בקבוצת האימון:
# First, predict from the train dataset
predicted_train = model.predict(x_train)
# Convert the scaled data back to the original values
predicted_train_rescaled = scaler.inverse_transform(predicted_train)
# Plot
# Pop the first 30 values from the timeseries
x_axis = dataset_train.index[30:]
# Visualize the predicted values against the actual data
# but first we need to convert back to the actual data
actual_train_rescaled = scaler.inverse_transform(y_train.reshape(-1, 1))
plt.plot(x_axis, actual_train_rescaled, 'b')
plt.plot(x_axis, predicted_train_rescaled, 'r')
plt.legend(['actual','predicted'])
plt.title("Actual vs predicted in the train dataset")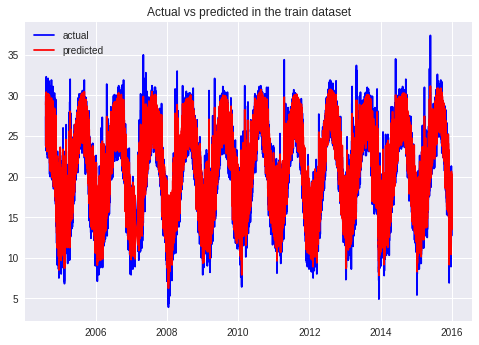
נראה בסדר, אבל מה שיעור הסטייה בין הערכים החזויים והערכים בפועל?
import math
from sklearn.metrics import mean_squared_error
# calculate root mean squared error
train_score = math.sqrt(mean_squared_error(actual_train_rescaled, predicted_train_rescaled))
print('Train Score: %.2f RMSE' % (train_score))Train Score: 1.30 RMSE
שיעור סטייה של 1.3 מעלות צלזיוס בין הערכים החזויים והערכים בפועל בנתונים שעליהם התאמן המחשב.
נחזור על התרגיל עבור קבוצת המבחן:
# Predict on the test dataset
predictions = model.predict(x_test)
# Convert back to the original values
predictions = scaler.inverse_transform(predictions)
# Plot
# Pop the first 30 values from the timeseries that
x_axis = dataset_test.index[30:]
# Visualize the predicted values against the actual data
# but first we need to convert back the actual data
actual_test_rescaled = scaler.inverse_transform(y_test.reshape(-1, 1))
# Visualize the predicted values against the actual data
plt.plot(x_axis, actual_test_rescaled, 'b')
plt.plot(x_axis, predictions, 'r')
plt.legend(['actual','predicted'])
plt.title("Actual vs predicted in the test dataset")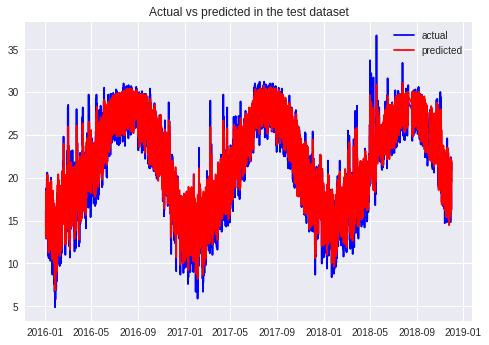
test_score = math.sqrt(mean_squared_error(actual_test_rescaled, predictions))
print('Test Score: %.2f RMSE' % (test_score))Test Score: 1.26 RMSE
שיעור הסטייה בקבוצת המבחן דומה מאוד לזו של קבוצת האימון מה שאומר שהמודל שלנו למד במידה הנכונה מה שמאפשר לו להסיק בצורה מדויקת למדי את התוצאות בקבוצת הניסוי.
סיכום
במדריך זה ראינו כיצד ניתן לחזות נתוני טמפרטורות בצורה מדויקת למדי אפילו שנתיים קדימה באמצעות שימוש בלמידת מכונה באמצעות TensorFlow מבוסס LSTM. אחרי שראינו שניתן להשתמש בשיטה זו על מנת להפיק תחזיות עבור תהליכים מחזוריים כדוגמת טמפרטורות, יהיה מעניין לנסות את השיטה על תופעות מחזוריות נוספות כדוגמת טמפרטורות, מחזור כתמי השמש, פרצי מגפות, ותחזיות כלכליות.
למידת מכונה מסוג RNN - Recurrent Neural Networks היא שימושית במיוחד בלימוד שפות אנושיות. מכיוון שסדר המילים הוא חשוב, וכאשר הסדר חשוב משתמשים ב-RNN. במדריך פיתוח מודל לאנליזת סנטימנט באמצעות למידת מכונה תוכלו לראות כיצד להשתמש ב-RNN כדי לחקות הבנת שפה אנושית טבעית על ידי המחשב.
לכל המדריכים בנושא של למידת מכונה
אהבתם? לא אהבתם? דרגו!
0 הצבעות, ממוצע 0 מתוך 5 כוכבים


המדריכים באתר עוסקים בנושאי תכנות ופיתוח אישי. הקוד שמוצג משמש להדגמה ולצרכי לימוד. התוכן והקוד המוצגים באתר נבדקו בקפידה ונמצאו תקינים. אבל ייתכן ששימוש במערכות שונות, דוגמת דפדפן או מערכת הפעלה שונה ולאור השינויים הטכנולוגיים התכופים בעולם שבו אנו חיים יגרום לתוצאות שונות מהמצופה. בכל מקרה, אין בעל האתר נושא באחריות לכל שיבוש או שימוש לא אחראי בתכנים הלימודיים באתר.
למרות האמור לעיל, ומתוך רצון טוב, אם נתקלת בקשיים ביישום הקוד באתר מפאת מה שנראה לך כשגיאה או כחוסר עקביות נא להשאיר תגובה עם פירוט הבעיה באזור התגובות בתחתית המדריכים. זה יכול לעזור למשתמשים אחרים שנתקלו באותה בעיה ואם אני רואה שהבעיה עקרונית אני עשוי לערוך התאמה במדריך או להסיר אותו כדי להימנע מהטעיית הציבור.
שימו לב! הסקריפטים במדריכים מיועדים למטרות לימוד בלבד. כשאתם עובדים על הפרויקטים שלכם אתם צריכים להשתמש בספריות וסביבות פיתוח מוכחות, מהירות ובטוחות.
המשתמש באתר צריך להיות מודע לכך שאם וכאשר הוא מפתח קוד בשביל פרויקט הוא חייב לשים לב ולהשתמש בסביבת הפיתוח המתאימה ביותר, הבטוחה ביותר, היעילה ביותר וכמובן שהוא צריך לבדוק את הקוד בהיבטים של יעילות ואבטחה. מי אמר שלהיות מפתח זו עבודה קלה ?
השימוש שלך באתר מהווה ראייה להסכמתך עם הכללים והתקנות שנוסחו בהסכם תנאי השימוש.