אתגר תכנותי: מציאת האורך של תת המערך העולה הארוך ביותר

עליך לכתוב פונקציה אשר מקבלת קלט מערך מספרים nums ומחזירה כפלט את האורך של תת המערך הארוך ביותר בו כל מספר גדול יותר מקודמו.

• את תת המערך עליו מבוסס הפלט ניתן ליצור על ידי מחיקת פריטים ממערך הקלט.

• אך אין לשנות את הסדר של המערך המקורי.

דוגמה 1:

Input: [1, 5, 2, 3, 8,7]
Output: 4

הסבר: תת המערך העולה הארוך ביותר הוא:

[1, 2, 3, 7]

• שאורכו הוא 4.

דוגמה 2:

Input: [4, 4, 4, 4]
Output: 1

איך פותרים?

ננסה לפתור בעזרת טבלת תכנות דינאמי שתצבור את האורכים כאשר מספר התאים בטבלה יהיה כמספר הפריטים במערך.

לדוגמה, אם המערך הוא:

[1, 5, 2, 3, 8,7]

אז נשתמש בטבלת `dp` (ר"ת של Dynamic Programming) כעין זו הכוללת 6 תאים (כמספר פריטי המערך):

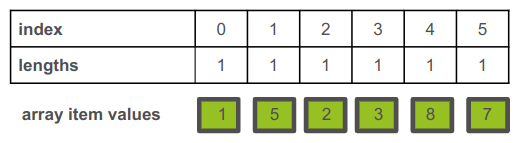
• בשורה הראשונה האינדקסים.

• בשורה השנייה האורכים הצבורים (length) כאשר כל תא מייצג את האורך המקסימלי של תת המחרוזת המסתיימת באינדקס זה.
  * הערך 1 כברירת מחדל בכל תא הוא בגלל שאורך תת המערך הוא לכל הפחות 1.

• מתחת לטבלה מיקמתי את מערך הקלט.

נשתמש בשני מצביעים (=סמנים) i ו-j:

• המצביע i שירוץ מאינדקס 1 ועד לסוף הטבלה.

• המצביע j שירוץ מאינדקס 0 ועד לתא אחד לפני זה בו נמצא i.

עדכון האורכים בטבלה dp יעשה רק בתנאי שהפריט במערך הקלט nums עליו מצביע i גדול יותר מזה עליו מצביע j כי אנחנו מעוניינים למצוא סדר עולה.

את המצביעים נקדם במסגרת איטרציות:

• איטרציה פותחת בקידום המצביע i בעמדה 1.

• המצביע j מתחיל בעמדה 0.

• המצביע j מתקדם צעד-צעד עד שהוא מגיע לפריט האחד לפני זה בו נמצא i (= i ו-j נוגעים).

• בצעד הבא אחרי המצב בו i ו-j נוגעים מסתיימת האיטרציה הנוכחית ומתחילה איטרציה חדשה.

באיטרציה הראשונה:

• המצביע i מצביע על אינדקס 1.

• j מצביע על אינדקס 0.

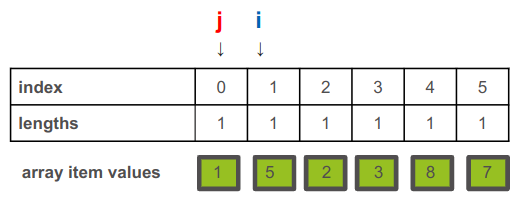
כיוון שהערך במערך עליו מצביע i גדול יותר מזה עליו מצביע j כי 5 גדול מ- 1 עומדות בפנינו 2 ברירות:

1. להוסיף 1 לאורך עליו מצביע j (מה שאומר שאורך תת המערך יהיה 2).

2. להשאיר את האורך בתא עליו מצביע i ללא שינוי .

במה בוחרים? במה שיותר ארוך כיוון שאנחנו מעוניינים למצוא את תת המערך הארוך ביותר.

len_current_dp_item = max(len_i, len_j+1)

במקרה שלנו, הוספת 1 לאורך עליו מצביע j נותנת 1+1=2 שזה ערך גבוה יותר מאשר זה עליו מצביע i שהוא 1, ולפיכך נשנה את האורך עליו מצביע i ל-2:

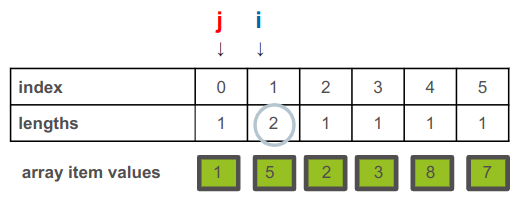
באיטרציה השנייה:

• המצביע i יצביע על אינדקס 2.

• המצביע j יתחיל מהצבעה על האינדקס 0.

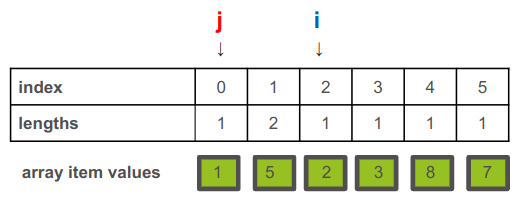
האם הערך עליו מצביע i גדול יותר מזה עליו מצביע j? התשובה היא כן כיוון ש-2 גדול מ-1.

כיוון שכן, נבחר בין 2 האפשרויות: להוסיף 1 לאורך עליו מצביע j או להשאיר את האורך עליו מצביע i ללא שינוי.

המקסימום בין 1+1 (האורך החדש הנובע מהוספת 1 לאורך עליו מצביע j) לבין 1 שהוא האורך המקורי עליו מצביע i הוא 2 לפיכך נעדכן את האורך:

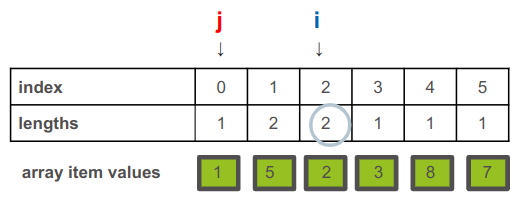
עדיין בתוך האיטרציה השנייה נקדם את הסמן j עמדה 1 לימין (את i נשאיר במקומו):

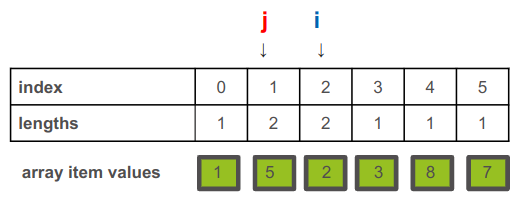
השוואה בין הערך עליו מצביע i לזה עליו מצביע j תלמד שהערך עליו מצביע j גדול יותר ועל כן אין לעדכן את האורך.

איטרציה 3:

נקדם את המצביע i עוד צעד 1 לימין, ואת j נחזיר לאינדקס 0:

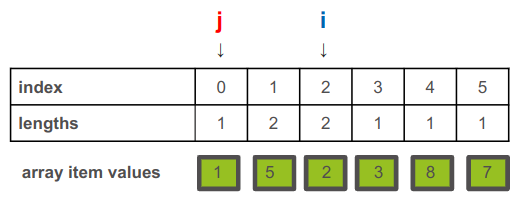
משווים בין הערכים עליהם מצביעים i ו-j, מעדכנים אם האורך עליו מצביע i אם מתקיימים שני התנאים: הערך בתא גבוה יותר וגם תוספת 1 לאורך עליו מצביע j גבוהה יותר מהאורך הנוכחי עליו מצביע i… מקדמים את j בכל פעם בצעד 1 עד שמגיע לתא הנמצא בדיוק לפני זה עליו מצביע i … וכשאין יותר לאן לקדם את j מקדמים את i ומסיגים את j לאינדקס 0 … וחוזר חלילה עד שמגיעים לסוף הטבלה.

בסופו של התהליך, כל תא בטבלה dp מייצג את האורך של תת המערך הארוך ביותר המסתיים בכל אינדקס.

לבסוף, מחזירים את הערך הגבוה ביותר מבין כל האורכים הצבורים בטבלה dp.

נקודד את הפתרון

ההסבר אולי נשמע מסובך אבל הקוד הרבה פחות מאיים.

• הפונקציה מקבלת את המערך nums בתור קלט, ודבר ראשון מחשבת את אורכו:

  def longest_increasing_subsequence(nums):
      len_nums = len(nums)
              

• את טבלת התכנות הדינמי dp המיועדת לצבור את אורכי תת המערכים ניצור כמערך:

  dp = [1] * (len_nums)

  • הערך ברירת המחדל של כל פריט במערך הוא 1 כיוון שזה האורך המינימלי של תת המערך.

• שתי לולאות ירוצו על מערך הקלט nums:

  1. חיצונית אשר תרוץ מאינדקס מספר 1 ועד לקצה תוך עדכון ערך המצביע i.
  2. פנימית אשר תרוץ מ-0 ועד לפריט הקודם למצביע i תוך עדכון ערך המצביע j.

  for i in range(1, len_nums):
      for j in range(0, i):

  • אם הערך במערך הקלט עליו מצביע i גדול יותר מזה עליו מצביע j יש לבחור את הגבוהה מבין 2 אפשרויות:

    1. האורך הנוכחי באינדקס עליו מצביע i.

    2. האורך באינדקס עליו מצביע j בתוספת 1.

  dp[i] = max(dp[j]+1, dp[i])

• לאחר שהלולאות יסיימו לרוץ הפונקציה תחזיר את הערך הגבוה ביותר מבין הפריטים של dp:

  return max(dp)

עכשיו הכול ביחד:

def longest_increasing_subsequence(nums):
    if not nums: # Handle edge case
        return 0

    len_nums = len(nums)

    dp = [1] * (len_nums)
        
    for i in range(1, len_nums):  # Loop through each element from the second to the last
        for j in range(0, i):    # Check all elements before the current element
            if nums[i] > nums[j]:  # Update the DP value only if nums[i] > nums[j]
                dp[i] = max(dp[j] + 1, dp[i])  # Choose the maximum length

    return max

נבדוק:

arr = [1, 2, 3]
print(longest_increasing_subsequence(arr)) # 3

arr = [10, 9, 2, 5, 3, 7, 101, 18] # 4 [2,3,7,101]
print(longest_increasing_subsequence(arr)) # 4

arr = [3, 10, 2, 1, 20]
print(longest_increasing_subsequence(arr)) # 3

arr = [30, 20, 10]
print(longest_increasing_subsequence(arr)) # 1

arr = [2, 2, 2]
print(longest_increasing_subsequence(arr)) # 1

arr = [10, 20, 35, 80]
print(longest_increasing_subsequence(arr)) # 4

arr = [1, 3, 2, 4]
print(longest_increasing_subsequence(arr)) # 3

arr = [0,8,4,12,2,10,6,14,1,9,5,13,3,11,7,15]
print(longest_increasing_subsequence(arr)) # 6

arr = [1, 2, 3, 4]
print(longest_increasing_subsequence(arr)) # 4

arr = [1, 5, 2, 3, 4]
print(longest_increasing_subsequence(arr)) # 4

הערכת יעילות

• יעילות המקום היא O(N) בגלל מספר הפריטים במערך dp שאורכו כאורך מערך הקלט num.
• יעילות הזמן היא O(N^2) בגלל שהפונקציה משתמשת בלולאה מקוננת שרצה על מערך dp באורך N.

לסיכום

מדריך זה מציג אתגר מהתחום של תכנות דינאמי אבל יותר מזה הוא מסביר כיצד ניתן לקחת בעיות "קשות ושעירות" ולהפוך אותם לפתירות על ידי שבירה לתתי בעיות קטנות שקל ופשוט לפתור.

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

תכנות דינמי מלמטה למעלה ובחזרה - מדריך לתכנות דינאמי שמתחיל מהבסיס

אלגוריתם דייקסטרה Dijkstra למציאת הנתיב הקצר ביותר בגרף ממושקל

פייתון מונחה עצמים 1: מחלקות, אובייקטים, תכונות ומתודות

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים