תכנות דינמי מלמטה למעלה ובחזרה - מדריך לתכנות דינאמי שמתחיל מהבסיס

השם "תכנות דינאמי" נשמע כמו שם לשיטת חינוך מחדש במשטרים אפלים אבל הבנה של הרעיונות בבסיס השיטה ואימון על פתרון אתגרים תכנותיים יכול להפוך את הנושא להרבה פחות מפחיד. במדריך זה נסביר את הרעיונות העומדים בבסיס השיטה של תכנות דינאמי וגם נציג בעיות קלאסיות ופתרונות שהכרתם יעזרו רבות לכל מתכנת שמעוניין להוסיף כלי חשוב ומשמעותי זה לארגז הכלים שלו.

תכנות דינמי (Dynamic Programming) היא גישה לפתרון בעיות מורכבות על ידי פירוק לבעיות משנה קטנות יותר, ופתרון כל בעיית משנה פעם אחת בלבד, תוך שמירת התוצאות כדי למנוע חישובים חוזרים.

כדי להשתמש בתכנות דינמי הבעייה התכנותית צריכה להיות בעלת תת מבנה אופטימלי וצריך שתהיה חפיפה בין בעיות המשנה. תת מבנה אופטימלי משמעותו שפתרון הבעיה צריך לנבוע משילוב הפתרונות לתת הבעיות. חפיפה בין בעיות המשנה משמעה שתת הבעיות חוזרות על עצמם בפתרון אז במקום לפתור כל פעם מחדש את אותה הבעיה, שומרים את הפתרון במבנה נתונים (טבלה או מערך), ואז כששוב נתקלים באותה תת בעיה שולפים את התוצאה ממבנה הנתונים במקום לפתור מחדש.

אתגר: חישוב המקום ה-nי בסדרת פיבונאצ'י

סדרת פיבונאצ'י היא רצף של מספרים שבו כל איבר שווה לסכום שני האיברים הקודמים בסדרה. המספרים הראשונים בסדרה הם:

Fibonacci Sequence = 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

• האיבר הראשון הוא 0, והשני הוא 1.
• כל איבר אחרי השני הוא חיבור של שני האיברים הקודמים.

התמונה הבאה מציגה חישוב של מספרי פיבונאצ'י עד למקום העשירי:

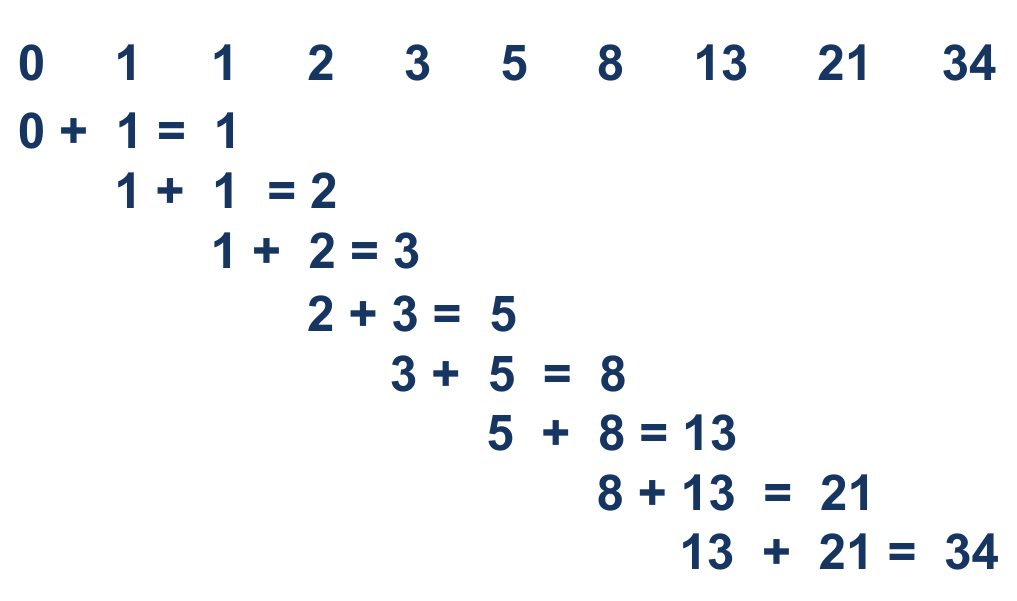
נסכם את הכללים למציאת איבר בסדרת פיבונאצ'י:

fib(0) = 0
fib(1) = 1
if n >=2 :
    fib(n) = fib(n - 1) + fib(n - 2)

כדי לחשב את n צריך קודם לחשב את n-1 ואת n-2, וכדי לחשב את n-1 צריך לחשב את n-2 ואת n-3. וכדי לחשב את n-2 צריך קודם כל לחשב את n-3 ואת n-4. התרשים הבא ממחיש את הרעיון:

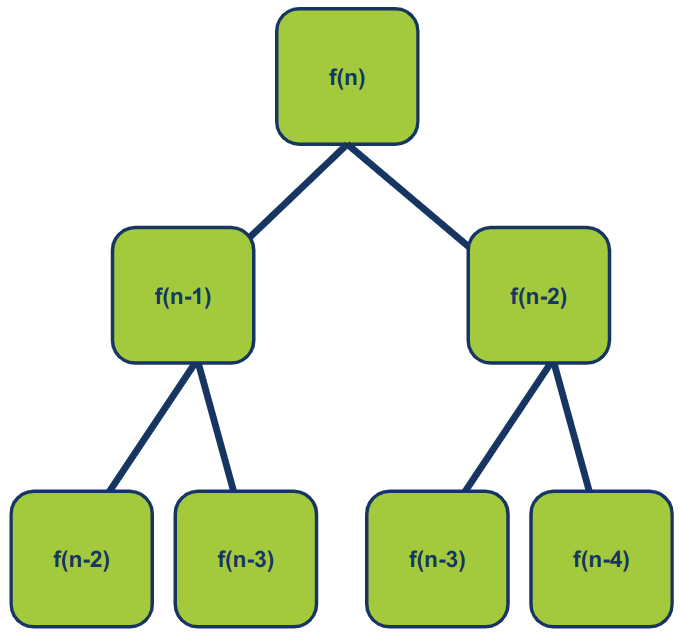
מהכללים לעיל מתבקש לכתוב פונקציה שקוראת לעצמה (=פונקציה רקורסיבית) לחישוב האיברים בסדרת פיבונאצ'י. נכתוב את הפונקציה עם תנאי בסיס ומקרה רקורסיבי (אם הנושא של רקורסיה לא ברור בבקשה לקרוא את המדריך בנושא רקורסיה):

def fib(n):    
    # Base cases
    if n < 2:
        return n
    # Recursive case
    else:
        return fib(n-1) + fib(n-2)

נבחן את הפונקציה למציאת האיבר ה-nי של סדרת פיבונאצ'י:

print(fib(1)) # 1
print(fib(4)) # 3
print(fib(9)) # 34

כל עוד ננסה לחשב n בעל ערך נמוך הפונקציה הרקורסיבית לעיל תעבוד. אבל אם ננסה לחשב עבור ספרות גבוהות יותר, נקבל האטה משמעותית בקבלת התוצאות עד כדי קריסה של המחשב. לדוגמה, ניסיתי להריץ את הפונקציה למציאת הספרה ה- 40 בסדרה:

import time


start = time.time()


def fib(n):
    if n < 2:
        return n
    else:
        return fib(n-1) + fib(n-2)
        
print(fib(40)) # 102334155


end = time.time()
print(f"Time elapsed {end - start} seconds")

אצלי על המחשב, משך הביצוע של הפונקציה היה 13 שניות. המון זמן!

פתרון אפשרי לבעיה הוא שימוש ב-Memoization.

Memoization היא שיטת להאצת תוכנות על ידי שמירת התוצאות של קריאות לפונקציה בקאש (=זיכרון מטמון), ואם נתקלים שוב באותם קריאות לפונקציה מחזירים את התוצאה מהקאש במקום לבצע מחדש את החישוב.

אבל למה שהפתרון יעבוד?

שימו לב שכדי למצוא את האיבר ה-nי בסדרת פיבונאצ'י יש חישובים שחוזרים על עצמם:

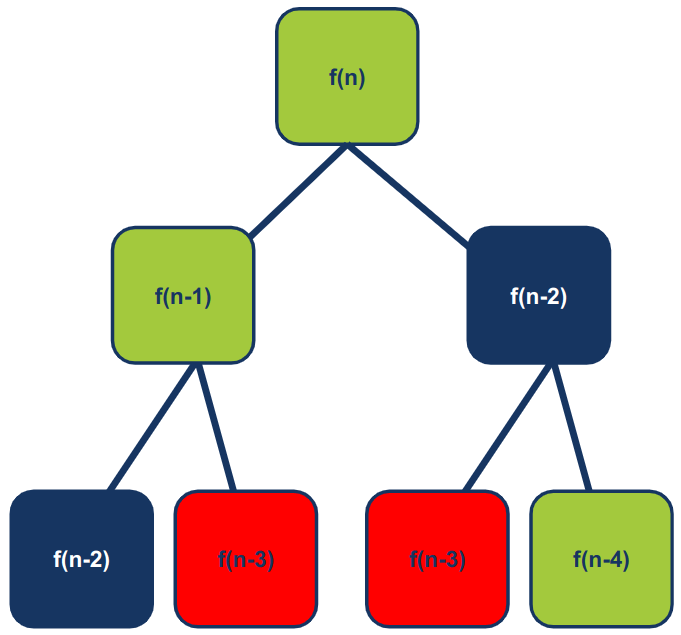
חישובים אילו שחוזרים על עצמם הם בדיוק מה שאנחנו צריכים כדי להשתמש ב-Memoization לייעול הפונקציה. לצורך היישום, נוסיף מילון dictionary שיהווה קאש. למילון נקרא memo, כי זה מה שמקובל, והוא יאחסן את התוצאות של חישוב הפתרונות לתתי הבעיות. בתוך המילון המפתחות יהיו הקלטים והערכים יהיו תוצאות החישוב:

# Dictionary to store cached Fibonacci values
memo = {}
def fib(n):
    # Check if the value is already in the cache
    if n in memo:
        return memo[n]
    
    if n < 2:
        result = n
    else:
        # Recursive case with memoization
        result = fib(n-1) + fib(n-2)
        
    # Cache the result before returning
    memo[n] = result
    return result

כשהרצתי את הפונקציה המצויידת בקאש memo משך הריצה היה 32 מיליוניות השנייה. שיפור של פי מיליונים… 😄

שתי גישות ליישום תכנות דינמי "מלמעלה למטה" ו"מלמטה למעלה"

קיימות שתי גישות ליישום תכנות דינאמי:

• Top-down מלמעלה למטה
• Bottom-up מלמטה למעלה

בגישת Top-down מזהים את הדפוס לפתרון הבעיה הגדולה ושוברים אותה באופן רקורסיבי לבעיות קטנות וקלות יותר לפתרון. גישת Top-down מכונה גם memoization, ובה השתמשנו כדי להאיץ את חישוב המספרים בסדרת פיבונאצ'י.

בגישת Bottom-up מבינים קודם כיצד לפתור את הבעיות הקטנות ומזה מסיקים כיצד לפתור את הבעיה הגדולה. הגישה משתמשת בעיקר בלולאות, והיא נחשבת ליעילה יותר. גישת Bottom-up מכונה גם tabulation (מלשון טבלה), ובהמשך נראה דוגמאות המיישמות את הגישה.

היתרון המרכזי של שימוש בגישת Top-down (=memoization) שהוא אינטואיטיבי להרבה בעיות. נחזור לפונקציה שכתבנו למציאת ספרות פיבונאצ'י שם ראינו שאת הפתרון אנחנו יכולים לכתוב במבנה דמוי עץ המייצג פעולות שחוזרות על עצמם, וזה בדיוק מה שרקורסיה עושה. מצד שני, קיימת סכנה של הצפת זיכרון, stack overflow, במקרה של ריבוי קריאות רקורסיביות. כדי למנוע את סכנת ה-stack overflow מוטב להשתמש בפתרון Bottom-up (=tabulation) המשתמש במערך או בטבלה שממלאים רק בפתרונות ההכרחיים לפתרון הבעיה.

נכתוב את הפונקציה לחישוב המספר ה-nי בסדרת פיבונאצ'י בגישה של "מלמטה למעלה" Bottom-up.

נתחיל כמו בפתרון מ"למעלה למטה" :

def fib(n):    
    if n < 2:
        return n

נוסיף טבלה, שבמקרה שלנו היא מערך:

def fib(n):
    if n < 2:
        return n
    
    # Initialize a list to store Fibonacci numbers
    fib_numbers = [0] * (n + 1)

• המערך יכיל את ספרות פיבונאצ'י ממקום 0 עד למקום ה-nי כי כדי לחשב ספרת פיבונאצ'י אנחנו זקוקים לחבר את 2 הספרות הקודמות לה ברצף.

נאכלס את הטבלה בערכי שני המספרים הראשונים בסדרה כדי שיהיה לנו מאיפה להתחיל:

def fib(n):
    if n < 2:
        return n
    
    # Initialize a list to store Fibonacci numbers
    fib_numbers = [0] * (n + 1)
    fib_numbers[0] = 0
    fib_numbers[1] = 1

בתוך לולאה נחשב את מספרי פיבונאצ'י אחד-אחד עד למקום ה-nי תוך שאנו מזינים למערך את המספרים המחושבים, ואח"כ שולפים את תוצאות החישובים עבור שני המספרים הקודמים כדי לחשב את האיבר הנוכחי:

def fib(n):
    if n < 2:
        return n
    
    # Initialize a list to store the Fibonacci numbers
    fib_numbers = [0] * (n + 1)
    fib_numbers[1] = 1
    
    # Calculate the numbers inside a loop based on the 2 previous numbers stored in the fib_numbers array.
    for i in range(2, n + 1):
        fib_numbers[i] = fib_numbers[i - 1] + fib_numbers[i - 2]

לבסוף, הפונקציה מחזירה את הספרה במקום ה-nי של המערך fib_numbers המהווה את תוצאת החישוב. כל פריט במערך הוא תוצאה של פתרון בעיית משנה, כאשר הפריט ה-nי מהווה את פתרון הבעיה הגדולה שאנו מעוניינים לפתור, ועל כן הפונקציה תחזיר את האיבר ה-nי:

def fib(n):
    if n < 2:
        return n
    
    # Initialize a list to store Fibonacci numbers
    fib_numbers = [0] * (n + 1)
    fib_numbers[1] = 1
    
    # Calculate the numbers inside a loop
    for i in range(2, n + 1):
        fib_numbers[i] = fib_numbers[i - 1] + fib_numbers[i - 2]
    
    return fib_numbers[n]

נבחן את הפונקציה לחישוב ספרת פיבונאצ'י במקום ה-nי:

# Test cases
print(fib(0))  # 0
print(fib(1))  # 1
print(fib(2))  # 1
print(fib(3))  # 2
print(fib(4))  # 3
print(fib(5))  # 5
print(fib(6))  # 8
print(fib(500))  # 139423224561697880139724382870407283950070256587697307264108962948325571622863290691557658876222521294125

פתרון האתגר מיישם גישה "מלמטה למעלה" על ידי מעבר באמצעות לולאה פעם אחת על כל מספרי פיבונאצ'י עד למספר הרצוי, ומילוי טבלה תוך כדי מעבר, מה שמקנה לתהליך יעילות זמן מצויינת של O(n) כיוון שהלולאה עוברת פעם אחת על כל האיברים מ-0 ועד ל-n. (אם הנושא החשוב של יעילות קוד, ואיך מסיקים אותו, לא ברור, מומלץ לקרוא את המדריך big-O ביטוי ליעילות הקוד).

ראינו איך פותרים אתגר של תכנות דינאמי. בוא ננסה לפתור עוד כמה שיסייעו לנו להבין איך השיטה עובדת כי הרבה פעמים בעיות מסוג תכנות דינאמי הם לא יותר מ"אותה הגברת בשינוי אדרת", רק צריך להתרגל. אז יאללה בוא ניתן בראש. נותרו עוד 5 אתגרים אותם צריך לפתור…

אתגר: כמה דרכים שונות לטפס מדרגות

אתה מטפס גרם מדרגות שיש בו n מדרגות. בכל פעם אתה יכול לטפס מדרגה אחת או שתיים. מהו מספר הדרכים לטיפוס לראש גרם המדרגות?

כתוב פונקציה בשם climb_stairs(n) המחזירה את המספר הכולל של הדרכים לטפס את המדרגות.

איך ניגשים לפתור כזה תרגיל? מאיפה להתחיל?

בוא ננסה לחשוב על כמה דוגמאות ואולי דרכם נגיע לפתרון:

• אם אין מדרגות אז יש 0 דרכים לטפס אותם.
• קיימת רק דרך 1 לטפס מדרגה 1.
• כדי לטפס 2 מדרגות אז אפשר לטפס כל מדרגה בנפרד או לטפס את 2 המדרגות בבת אחת, ומכאן 2 דרכים.
• כדי לטפס 3 מדרגות אפשר לטפס מדרגה-מדרגה, או 2 מדרגות ואז 1, או מדרגה 1 ואז 2. סה"כ 3 דרכים.

אני רוצה להתעכב על הדוגמה של 3 מדרגות כי חישוב מספר הדרכים הוא שילוב של מספר הדרכים לטפס מדרגה 1 ועוד מספר הדרכים לטפס 2 מדרגות. אז אם מה שאני רוצה הוא לחשב את מספר הקומבינציות האפשריות לטיפוס מדרגות וידוע לי שיש 2 דרכים לטיפוס 2 מדרגות ודרך 1 לטפס מדרגה אחת אז אני יכול לחבר את מספר הדרכים, ולקבל: 1 + 2 = 3. משמע 3 דרכים לטיפוס 3 מדרגות.

לפי אותו היגיון, כדי לחשב את מספר הדרכים לטפס 4 מדרגות אני צריך לדעת כמה דרכים יש לטיפוס 2 ו-3 מדרגות, ואז לחבר את מספר הדרכים.

ושוב לפי אותו היגיון, כדי לחשב את מספר הדרכים לטפס 5 מדרגות אני צריך לדעת כמה דרכים יש לטיפוס 3 ו-4 מדרגות, ואז לחבר את מספר הדרכים.

אז לפי אותו היגיון אינדוקטיבי, נסיק כלל עבור כל מספר n של מדרגות. כאשר הכלל אומר שכדי לדעת כמה דרכים קיימות לטפס את המקרה הנוכחי של n מדרגות יש לחבר את 2 המקרים שלפני הנוכחי, n-1 ו n-2 , וזה ממש מזכיר את מה שעשינו עם פיבונאצ'י.

נכתוב את הפתרון:

def climb_stairs(n):
    if n < 0:
        raise ValueError("A staircase can't have less than zero stairs")

    if n < 2:
        return n

    cache = {}
    # Cache the trivial cases
    cache[0] = 0
    cache[1] = 1
    cache[2] = 2
    
    # Build the cache as you go bottom up
    for i in range(3, n+1):
        cache[i] = cache[i-1] + cache[i-2]
    
    # The answer is in the last cell
    return cache[n]

נבחן את הפתרון שכתבנו:

# Test cases

print(climb_stairs(0)) # 0
print(climb_stairs(1)) # 1
print(climb_stairs(2)) # 2
print(climb_stairs(3)) # 3
print(climb_stairs(4)) # 5
print(climb_stairs(5)) # 8

נסביר את הפתרון:

1. הבעיה מחולקת לבעיות משנה: מציאת מספר הדרכים לטפס n מדרגות על ידי התחשבות במקרים קטנים יותר (n-1 ו n-2 כדי למצוא את n).
2. מטמון (cache) משמש לאחסון התוצאות של בעיות המשנה, דבר המונע חישובים חוזרים. זהו מאפיין של תכנות דינמי.
3. הפתרון חוזר בצורה איטרטיבית מלמטה למעלה, החל מהמקרים הטריוויאליים (cache[0], cache[1] ו-cache[2]) תוך צבירת הפתרונות עד להגעה לאיבר ה- nי על ידי הוספת התוצאות של בעיות משנה קטנות יותר.
4. לבסוף, התשובה מתקבלת מהמטמון. ספציפית מהפריט האחרון במטמון cache[n].

כל פריט במערך הוא תוצאה של פתרון בעיית משנה, כאשר הפריט ה-nי מהווה את פתרון הבעיה הגדולה שאנו מעוניינים לפתור, ועל כן הפונקציה מחזירה את האיבר ה-nי.

יופי פתרנו. להזמין את החבר'ה, לעשות מסיבה? רגע. קודם נבדוק אם הפתרון יעיל.

הפתרון דורש n מהלכים, כמספר האיברים מה שאומר סיבוכיות זמן O(n). בנוסף, השתמשנו במערך באורך n פריטים מה שאומר שהפונקציה דורשת סיבוכיות מקום O(n). סיבוכיות זמן ומקום לינאריים מעידים על היעילות הרבה של פתרון הבעיה.

אתגר: מספר המטבעות המינימלי הדרוש להגעה לסכום

נותנים לך מערך מטבעות coins המייצג ערכים שונים של מטבעות ומספר שלם amount המייצג סכום כסף כולל. עליך לקבוע את מספר המטבעות המינימלי הדרוש להשלמת סכום זה. אם לא ניתן להשלים את הסכום באמצעות המטבעות הנתונים, הפונקציה תחזיר -1.

למזלנו, מספר המטבעות מכל סוג אינו מוגבל.

כתוב פונקציה min_coins(coins, amount) שתפתור את הבעיה.

פתרון:

בשביל להתחיל מאיפה שהוא נחשוב על מספר מקרים:

• נאמר אם אין מטבעות, ואנחנו נדרשים להשלים סכום של 3 אז אין דרך לחשב, והפונקציה תחזיר -1.
• בהינתן סט מטבעות 1, 3, 4 כדי להשלים סכום של 5 אנחנו לכל הפחות זקוקים ל-2 מטבעות כיוון ש 1 + 4 = 5.
• בהינתן סט מטבעות 2 ו-4 אם אנחנו רוצים להשלים 3 אז אנחנו לא יכולים. לכן הפונקציה תחזיר -1.
• בהינתן סט מטבעות 1, 3, 4 כדי להשלים סכום של 6 אנחנו זקוקים לכל הפחות לשתי מטבעות. פעמיים 3.

את זה אנחנו צריכים לתרגם לקוד מה שאומר שאנחנו מעוניינים לכתוב תהליך שיעבוד בשלבים.

הפתרון הראשון שקופץ לראש הוא שימוש באלגוריתם חמדן לפיו בכל שלב ניקח את המטבע בעל הערך הנקוב הגבוה ביותר שנכנס לסכום. לדוגמה, בהינתן סט מטבעות 1, 3, 4 כדי להשלים סכום של 5 בשלב ראשון נבחר במטבע בעל הערך הכי גבוה 4, מה שמשאיר אותנו עם הפרש של 1 מהסכום שאותו אין לנו ברירה אלא להשלים עם מטבע בערך נקוב של 1. זה מקרה שעובד.

ננסה לפתור באמצעות אלגוריתם חמדן מקרה נוסף. בהינתן סט מטבעות 1, 3, 4 צריך להשלים סכום של 6. נבחר בשלב ראשון את המטבע בעל הערך הכי גבוה שהוא 4, ובשלב השני אין לנו ברירה אלא לבחור במטבע של 1, ואז בשלב השלישי נבחר שוב מטבע של 1. סה"כ 3 מטבעות. אבל זה לא הפתרון האופטימלי כיוון שניתן להשלים סכום של 6 באמצעות 2 מטבעות של 3. דוגמה נגדית זו מלמדת שאלגוריתם חמדן לא מתאים לפתרון הבעיה שעל הפרק.

אז מה אנחנו כן יכולים לעשות? ננסה להשתמש בתכנות דינמי.

מכיוון שראינו שהכי כדאי לעבוד מ"למטה למעלה" אנחנו צריכים קאש. זו נראית בעיה שאפשר לפתור אותה באמצעות מבנה נתונים חד ממדי, דוגמת מערך פשוט או מילון, מכיוון שאנחנו מעוניינים להשלים סכום ללא צורך להתחשב בממד נוסף. אורך המערך יהיה כאורך הסכום הרצוי כיוון שאת התשובה נבנה מהסכום הנמוך ביותר האפשרי ועד לסכום הרצוי בקפיצות של 1.

לדוגמה, בהינתן הסכום 6 ניצור מערך עם 7 תאים 0 עד 6:

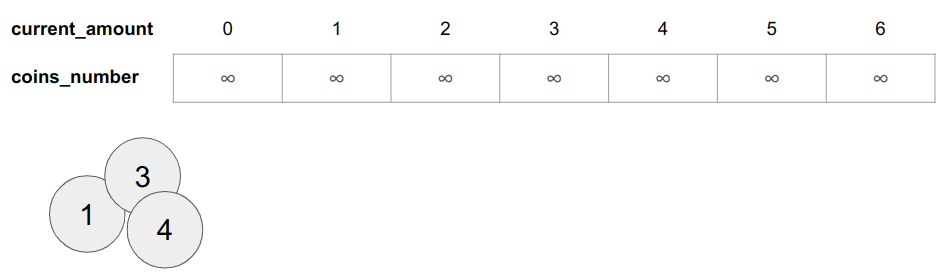
• current_amount - מחזיק את הסכומים התורנים אותם יש לחשב עד שמגיעים לפתרון. מתחילים מסכום 0 ומתקדמים עד לסכום הרצוי של 6.
• coins_number - הוא מספר המטבעות הדרושים להשלמת הסכום התורן.
• כל תא מייצג תת פתרון אחד: התא הראשון פתרון עבור סכום 0, תא שני פתרון עבור סכום של 1, התא האחרון מייצג את הפתרון, אם קיים, עבור סכום n שמעניין אותנו.
• נאתחל את המערך עם מספר מטבעות אינסופי בכל תא כי הבעיה דורשת לחשב את ערך המינימום בכל תא, עבור כל תת בעיה, ולפיכך ערך אינסוף מעיד על כך שלא פתרנו את תת הבעיה.

נאתחל את המערך עם ערך אינסוף בכל אחד מהתאים:

# Create a table to store the minimum number of coins needed to make up each amount.
dp = [float('inf')] * (amount + 1)

כרגיל אנחנו מתחילים מהמקרה הטריוויאלי. נציב ערך 0 בפריט הראשון של המערך כיוון שסכום 0 דורש 0 מטבעות להשלמתו:

# Create a table to store the minimum number of coins needed to make up each amount.
dp = [float('inf')] * (amount + 1)
dp[0] = 0

נעבור בתוך לולאה על כל אחד מהסכומים התורנים 1 עד n (כאשר n הוא הסכום המבוקש):

# Iterate over the amounts from 1 to the total amount.
for current_amount in range(1, amount + 1):

בתוך הלולאה החיצונית נריץ לולאה פנימית שתבדוק עבור כל אחד מהמטבעות אם הוא הוא נכנס בסכום התורן:

# Iterate over the amounts from 1 to the total amount.
for current_amount in range(1, amount + 1):
    # For each coin, check if it is possible to make up the current amount using that coin.
    for coin in coins:
        if current_amount - coin >= 0:

אם המטבע נכנס בסכום התורן אז: (1) נוסיף 1 למספר המטבעות הידוע מהקאש עבור המצב בו לא משתמשים במטבע, ו-(2)נציב את הערך המתקבל בתור ערך התא הנוכחי, אם הוא נמוך יותר מערך התא הנוכחי:

# Iterate over the amounts from 1 to the total amount.
for current_amount in range(1, amount + 1):
    # For each coin, check if it is possible to make up the current amount using that coin.
    for coin in coins:
        if current_amount - coin >= 0:
            # If it is possible, then update the minimum number of coins needed to make up the current amount.
            dp[current_amount] = min(1 + dp[current_amount - coin], dp[current_amount])

יותר לאט:

• התנאי שואל אם ערך המטבע נכנס בסכום התורן:

  if current_amount - coin >= 0:

• אם המטבע נכנס לתוך הסכום התורן, נוסיף מטבע 1 למספר המטבעות הדרושים להשלמת הסכום ללא תוספת ערך המטבע:

  1 + dp[current_amount - coin]

• נשווה את הערך המחושב בסעיף הקודם עם הערך הקיים בפריט הנוכחי במערך dp, ונציב את הנמוך מבין השניים בתור ערכו של הפריט:

  dp[current_amount] = min(1 + dp[current_amount - coin], dp[current_amount])

אחרי שהלולאה סיימה לרוץ אם מספר המטבעות המחושב המופיע בתא האחרון של הקאש, המייצג את הסכום הרצוי, שונה מאינסוף נחזיר אותו. אחרת, נחזיר -1:

# If the minimum number of coins needed to make up the total amount is infinity, then it is not possible to make up the amount.
if dp[amount] == float('inf'):
    return -1

# Otherwise, return the minimum number of coins needed to make up the total amount.
return dp[amount]

עכשיו הכל ביחד:

from typing import List

def min_coins(coins: List, amount: int) -> int:
    if len(coins) == 0: return 0
    
    # We will use dynamic programming to solve this problem.
    # Since we have observed that it's best to work from bottom to top, we need a cache.
    # This problem can be solved using a one-dimensional data structure like a simple array or dictionary,
    # as we want to complete the sum without considering an additional dimension.
    # The length of the array will be the same as the desired amount, as the answer is built from the lowest possible sum to the desired sum in increments of 1.

    # Initialize an array to store the minimum number of coins needed for each amount.
    dp = [float('inf')] * (amount + 1)

    # We'll start from the trivial case, setting the value 0 for the first element in the array since a sum of 0 requires 0 coins:
    dp[0] = 0

    # Iterate over the amounts from 1 to the total amount.
    for current_amount in range(1, amount + 1):
        # For each coin denomination, check if it can be used to make up the current amount.
        for coin in coins:
            # If the coin can be used, calculate the number of coins needed for the current amount.
            if current_amount - coin >= 0:
                # Update the minimum number of coins needed for the current amount.
                dp[current_amount] = min(1 + dp[current_amount - coin], dp[current_amount])

    # If the minimum number of coins needed to make up the total amount is still infinity,
    # it means it's not possible to make up the amount with the given coins.
    if dp[amount] == float('inf'):
        return -1

    # Otherwise, return the minimum number of coins needed to make up the total amount.
    return dp[amount]

נבחן את הפתרון שכתבנו:

# Test cases

coins = [1, 4, 3]
amount = 6
print(min_coins(coins, amount)) # 2

coins = [1, 3, 4]
amount = 5
print(min_coins(coins, amount)) # 2

coins = [1, 4, 5]
amount = 13
print(min_coins(coins, amount)) # 3

coins = [1, 4, 5]
amount = 157
print(min_coins(coins, amount)) # 32

coins = [1, 5, 10, 25]
amount = 30
print(min_coins(coins, amount)) # 2

coins = [2, 4]
amount = 3
print(min_coins(coins, amount)) # -1

coins = []
amount = 3
print(min_coins(coins, amount)) # 0

נמחיש את החישוב באמצעות סט מטבעות 1, 3, 4 כשהיעד הוא להשלים לסכום 6 , ואת עיקר העבודה עושות השורות הבאות אותם לקחתי מתוך הקוד:

# Iterate over the amounts from 1 to the total amount.
for current_amount in range(1, amount + 1):
        # For each coin, check if it is possible to make up the current amount using that coin.
        for coin in coins:
            if current_amount - coin >= 0:
                # If it is possible, then update the minimum number of coins needed to make up the current amount.
                dp[current_amount] = min(1 + dp[current_amount - coin], dp[current_amount])

1. הפריט הראשון במערך dp הוא 0 (כי הסכום התורן הוא 0).

   המערך dp כולל עכשיו את האיברים:

   [0, ∞, ∞, ∞, ∞, ∞, ∞]

2. הפריט השני במערך מכיל את מספר המטבעות הדרושים להשלמת הסכום התורן current_amount של 1. נעבור על כל המטבעות אחד אחד החל ממטבע בערך 1:

   • האם אפשר להכניס 1 לסכום התורן שהוא 1? כן. כדי לחשב את כמות המטבעות בתא (=המשלימות לסכום התורן) נוסיף 1 לכמות המטבעות במצב בו לא הוספנו את המטבע. המצב בו לא הוספנו את המטבע נמצא בתא שסכומו 0, והוא מכיל 0 מטבעות. לכן, 0 + 1 = 1. סכום זה נמוך מ-∞ הדיפולטי, על כן נציב בתא # 1, את הערך 1 המייצג את מספר המטבעות המינימלי האפשרי עבור סכום של 1. 
   • המטבעות 3 ו-4 אינם באים בחשבון כיוון שערכם גבוה מדי.

   המערך dp כולל עכשיו את האיברים:

   [0, 1, ∞, ∞, ∞, ∞, ∞]

3. פריט המערך השלישי מכיל את מספר המטבעות הדרושים להשלמת סכום תורן של 2. נעבור על סט המטבעות אחד אחד, 1 ← 3 ← 4:

   • האם ניתן להכניס מטבע בערך נקוב 1? כן. נוסיף 1 למספר המטבעות הדרושים להשלמת סכום 1, אותו חישבנו בצעד הקודם: 1 + 1 = 2. נציב את מספר המטבעות המחושב (2) בתור ערך פריט המערך כיוון שערך זה נמוך מהערך ברירת המחדל ∞.
   • המטבעות 3 ו-4 אינם רלוונטיים כיוון שערכם גבוה מהדרוש.

   המערך dp כולל עכשיו את האיברים:

   [0, 1, 2, ∞, ∞, ∞, ∞]

4. פריט המערך הרביעי מכיל את מספר המטבעות הדרושים להשלמת הסכום התורן ל- 3. נעבור על סט המטבעות אחד אחד:

   • האם ניתן להכניס מטבע בערך נקוב 1? כן. נוסיף 1 למספר המטבעות הדרושים להשלמת סכום 2, אותו כבר חישבנו בצעד הקודם (=2). נחבר 2 + 1 = 3. נציב את מספר המטבעות המחושב (3) בתור ערך פריט המערך כיוון שערך זה נמוך מ-∞ הדיפולטי.
   • נמשיך לבדיקת מטבע בערך 3 כאשר מספיק מטבע 1 למלא את הסכום התורן. כיוון שמטבע 1 הוא פחות מערך של 3 המופיע במערך נעדכן את הערך.
   • מטבע בערך נקוב 4 אינו רלוונטי.

   המערך dp כולל עכשיו את האיברים:

   [0, 1, 2, 1, ∞, ∞, ∞]

5. פריט המערך החמישי מכיל את מספר המטבעות הדרושים להשלמת הסכום התורן ל-4. נעבור על סט המטבעות אחד אחד:

   • האם ניתן להכניס מטבע בערך נקוב 1? כן. נוסיף 1 למספר המטבעות הדרושים להשלמת סכום 3: 1 + 1 = 2. נציב 2 במקום ∞ בתא.
   • האם ניתן להכניס מטבע בערך נקוב 3? כן. נוסיף 1 למספר המטבעות הדרושים להשלמת סכום של 1: 1 + 1 = 2. 2 שווה לערך הנוכחי בתא, ועל כן אין צורך לשנות את ערך התא. 
   • האם ניתן להכניס מטבע בערך נקוב 4? כן. נוסיף 1 למספר המטבעות הדרושים לסכום 0. 0 + 1 = 1. 1 נמוך מהערך הקיים בתא, ועל כן נעדכן את ערך התא ל-1.

   המערך dp כולל עכשיו את האיברים:

   [0, 1, 2, 1, 1, ∞, ∞]

6. פריט המערך השישי מכיל את מספר המטבעות הדרושים להשלמת הסכום התורן ל-5. נעבור על סט המטבעות אחד אחד:

   • האם ניתן להכניס מטבע בערך נקוב 1? כן. נוסיף 1 למספר המטבעות הדרושים להשלמת סכום 4: 1 + 1 = 2. נציב 2 במקום ∞ בתא. 
   • האם ניתן להכניס מטבע שערכו 3? כן. נוסיף 1 למספר המטבעות הדרושים להשלים סכום 2: 2 + 1 = 3. 3 גדול ממספר המטבעות בתא ולכן לא נעדכן. 
   • האם ניתן להכניס לתא מטבע שערכו 4? כן. נוסיף 1 למספר המטבעות הדרושים להשלמת סכום של 1: 1+ 1 = 2. 2 שווה למספר המטבעות בתא אז אין צורך לעדכן.

   המערך dp כולל עכשיו את האיברים:

   [0, 1, 2, 1, 1, 2, ∞]

7. פריט המערך השביעי מכיל את מספר המטבעות הדרושים להשלמת הסכום התורן 6. נעבור על סט המטבעות אחד אחד:

   • האם ניתן להכניס מטבע בערך נקוב 1? כן. נוסיף 1 למספר המטבעות הדרושים להשלמת סכום 5: 1 + 2 = 3. נציב 3 במקום ∞ בתא. 
   • האם ניתן להכניס מטבע בערך נקוב 3? כן. נוסיף 1 למספר המטבעות הדרושים להשלמת סכום 3: 1 + 1 =2. 2 נמוך מ-3, ועל כן נעדכן את ערך התא ל-2.
   • האם ניתן להכניס לתא מטבע שערכו 4? כן. נוסיף 1 למספר המטבעות הדרושים להשלמת סכום 2: 1 + 2 = 3. הערך המחושב גבוה מערך התא, ועל כן אין צורך לעדכן.

סיימנו לרוץ על כל פריטי הסכומים התורנים ועכשיו נוכל להחזיר את הערך בתא האחרון של המערך אשר מהווה את פתרון הבעיה.

הפונקציה עובדת. האם היא יעילה?

סיבוכיות הזמן: "m" מייצג את מערך הסכומים הדרושים להרכבת הפתרון, ו-"n" את מספר הערכים השונים של מטבעות זמינים. הלולאה החיצונית רצה מ-1 ל- "m", מה שגורם ל-O(m) חזרות. בתוך הלולאה החיצונית רצה לולאה פנימית n פעמים עבור כל סכום תורן. מה שתורם O(n) חזרות. ביחד, סיבוכיות הזמן הכוללת היא O(m * n).

סיבוכיות המקום: המשתנה הדורש מקום בזיכרון משמעותית מעל לכל היתר הוא המערך "dp" שאורכו m על פי הסכום. בהתאם, סיבוכיות המקום היא O(m).

אתגר: חישוב סכום מסלול מינימלי

בהינתן רשת של מספרים חיוביים, מצא מסלול מהפינה השמאלית העליונה לפינה הימנית התחתונה הממזער את סכום המספרים לאורך המסלול. אתה יכול לעבור רק למטה או ימינה.

לדוגמה, בהינתן הרשת:

[
 [1,3,1],
 [1,5,1],
 [4,2,1]
]

סכום המסלול המינימלי מהפינה השמאלית העליונה לפינה הימנית התחתונה הוא 7 (1 → 1 → 1 → 3 → 1).

ניתן לפתור בעיה זו בצורה יעילה באמצעות תכנות דינמי. הרעיון המרכזי הוא לבנות טבלה שבה כל תא (i, j) מייצג את סכום המסלול המינימלי שמגיע לתא זה. הערך בכל תא נקבע על ידי התחשבות במינימום של סכום המסלול מהתא שמעליו (i-1, j) וסכום המסלול מהתא משמאלו (i, j-1).

אתה מוזמן לנסות לפתור בעצמך. הפתרון בהמשך.

פתרון:

אנחנו יודעים לעבוד בתכנות דינמי בגישה של "מלמטה למעלה" מה שאומר שמתחילים לפתור את תת הבעיה הכי קטנה שאפשר, הכי טריוויאלית, שאח"כ מרחיבים אותה לפתרונות של בעיות קטנות דומות בסדרה של צעדים המצטברים עד לפתרון המלא.

מה המקרה הכי טריוויאלי? אם אתה מתחיל בתא השמאלי העליון, כי כך אתה חייב להתחיל על פי תנאי האתגר, הערך הוא בהכרח 1 כי אתה לא יכול להגיע לתא זה משום תא אחר (אתה לא יכול להגיע לא מלמעלה ולא משמאל כי אין תאים כאלה, והמעבר מותר רק למטה או לימין).

מהתא השמאלי העליון אנחנו יכולים לעבור רק למטה או ימינה לפי תנאי הבעיה. אם נעבור לתא מימין או נעבור לתא מלמטה אז אחרי שעברנו לתאים החדשים גם מהם אנחנו יכולים לעבור רק ימינה או למטה. אנחנו מבינים שאנחנו נעים בשני ממדים, ימינה (אופקי) או למטה (אנכי), ומכאן שלצורך הפתרון דרוש לנו מבנה נתונים דו-מימדי, המדמה טבלה. טבלה, table, מזכיר tabulation ואנחנו מכירים גישה "מלמטה למעלה" של תכנות דינאמי המשתמשת ב-tabulation.

עד כה עבדנו עם מבני נתונים חד ממדיים, דוגמת מילון או מערך פשוט אבל באתגר זה אנחנו פוגשים בפעם הראשונה בטבלה דו-מימדית לה נקרא, כרגיל, dp. האורך והרוחב של הטבלה יוגבל על ידי מספר התאים בטבלה המקורית, ובמקרה שלנו האורך הוא 3 בכל כיוון. 3 עמודות במישור האופקי, ו- 3 שורות במישור האנכי:

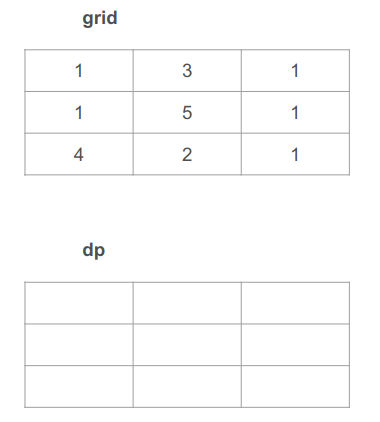
הטבלה הדו מימדית תורכב מפתרונות של תתי הבעיות. כל תא פותר את אחת מתת הבעיות בדרך לפתרון הבעיה הגדולה.

זה משפט חשוב אז נקרא אותו שוב:

הטבלה הדו מימדית תורכב מפתרונות של תתי הבעיות. כל תא פותר את אחת מתת הבעיות בדרך לפתרון הבעיה הגדולה.

הערך של התא השמאלי העליון ידוע לנו שהוא 1 (ע"פ הרשום ב-grid) כי אין אפשרות אחרת:

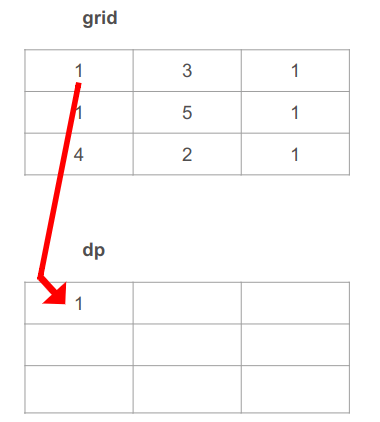
כדי לעבור מהתא השמאלי העליון ימינה יהיה עלינו להוסיף 3 ל-1. 1 + 3 = 4. 3 מהתא המתאים ב- grid ו-1 מהתא משמאל לנוכחי ב- dp :

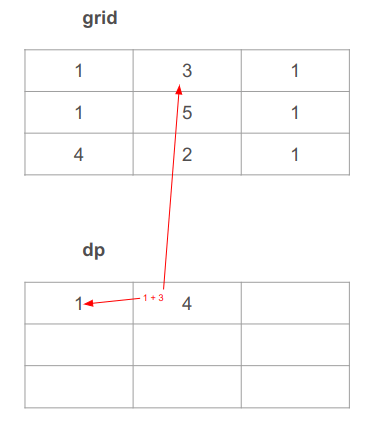
• אנחנו מוסיפים לערך התא משמאל בטבלה dp ולא לתא שמעל כי אין שורה מעל.

נעבור עוד צעד אחד ימינה, ונחשב את ערך התא הימני העליון שהוא 4 + 1 = 5. 4 מהתא שמשמאל ו-1 מהתא המקביל ב-grid:

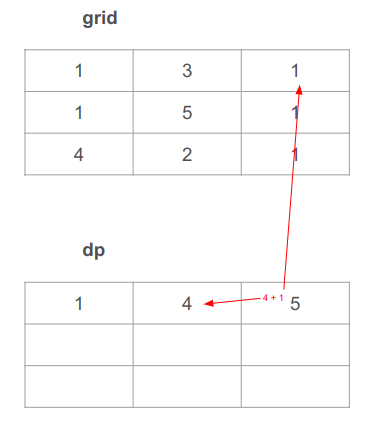
באופן דומה, נמלא את הערכים של העמודה השמאלית. לשם כך, אנחנו כל הזמן עוברים למטה, מה שאומר שערך התא הנוכחי מחושב מתוספת של ערך התא מלמעלה ב- grid לערך התא הנוכחי ב- dp (אנחנו לא לוקחים בחשבון את ערך התאים משמאל מכיוון שאין עמודה משמאל).

נרד עמדה אחת מהתא השמאלי העליון מה שאומר נתיב באורך 1 + 1 = 2. 1 מהתא שמעל ב- dp ו-1 מהתא המקביל ב-grid:

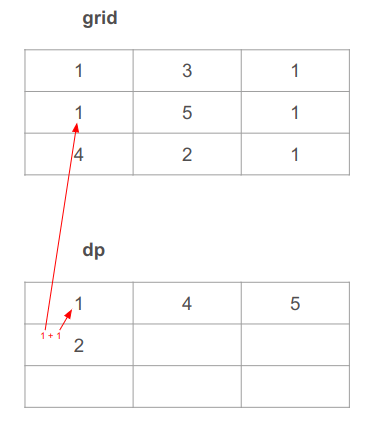
נרד עמדה אחת נוספת, עדיין בעמודה השמאלית, ונחשב נתיב באורך 2 + 4 = 6. 2 מהתא שמעל ב- dp ו-4 מהתא המקביל ב-grid:

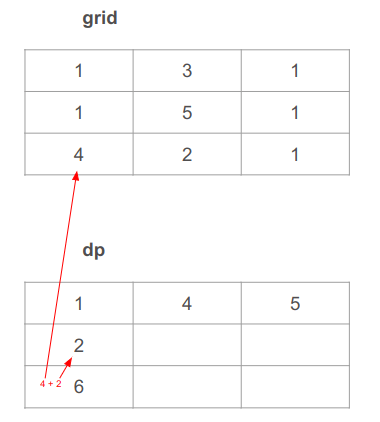
עד פה המקרים היותר פשוטים. נעבור לחישוב המקרים הקצת יותר מורכבים.

אנחנו עוברים למלא את התאים הפנימיים של הטבלה, בהם נצטרך לבחור בין שתי אפשרויות:

1. תוספת ערך התא הקיים ב-grid לערך התא מעל ב-dp
2. תוספת ערך התא הקיים ב-grid לערך התא משמאל ב-dp

מכיוון שאנו מעוניינים בחישוב הנתיב המינימלי ניקח את הערך הקטן בין שתי האפשרויות.

נפתור את תת הבעיה בתא (1, 1). בשני המקרים אנחנו צריכים להוסיף 5 כי זה הערך של התא (1, 1) ב-grid.

1. במקרה הראשון, נוסיף 5 לערך התא מעל ב-dp שערכו 4. נחשב: 5 + 4 = 9.
2. במקרה השני, נוסיף 5 לערך התא משמאל ב-dp שערכו 2. נחשב: 5 + 2 = 7.

הערך המינימלי בין שתי האפשרויות, 7 ו-9, הוא 7, אז נמלא בערך זה את התא:

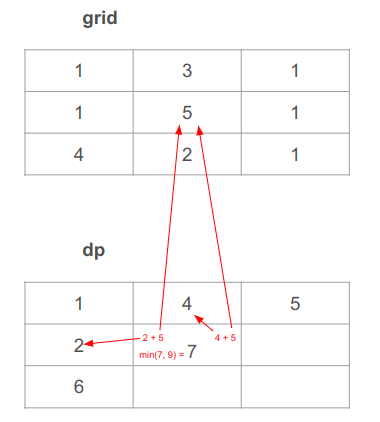
נחשב את התא הקיצוני מימין בשורה האמצעית. לשני המקרים הנשקלים נוסיף 1 מה-grid. נוסיף 1 לערך התא משמאל: 1 + 7 = 8. נוסיף אחד לערך התא מעל: 1 + 5 = 6. נבחר בערך המינימלי בין 8 ל-6, שהוא 6:

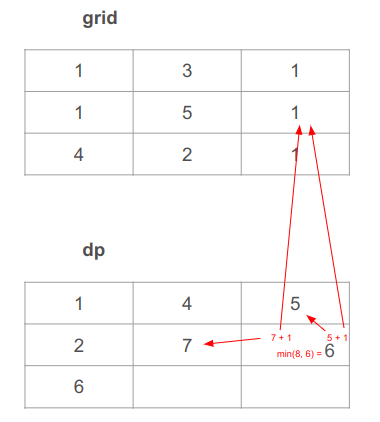
נרד שורה.

נחשב את התא האמצעי בשורה התחתונה. לשני המקרים הנשקלים נוסיף 2 מה-grid. נוסיף 2 לערך התא משמאל: 2 + 6 = 8. נוסיף 2 לערך התא מעל: 2 + 7 = 9. נבחר בערך המינימלי בין 8 ל-9, שהוא 8:

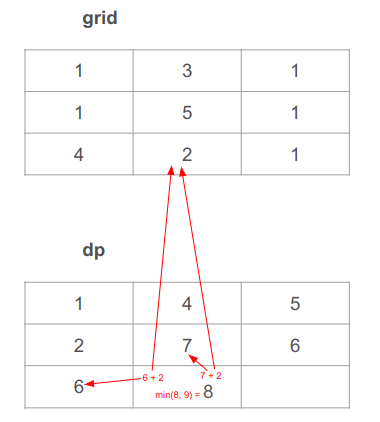
נחשב את התא האחרון של הטבלה. לשני המקרים הנשקלים נוסיף 1 מה-grid. נוסיף 1 לערך התא משמאל 1 + 8 = 9. נוסיף 1 לערך התא מעל 1 + 6 = 7. נבחר בערך המינימלי בין 7 ל-9 , שהוא 7:

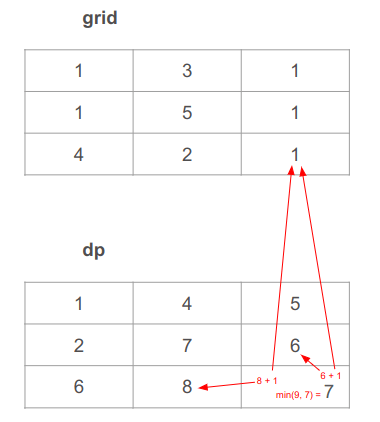
הערך המחושב בתא "האחרון" של טבלת התכנות הדינמי dp, במקרה שלנו בתא הימני התחתון, הוא התשובה לשאלה. וזה גם מה שהפונקציה תחזיר.

נכתוב את קוד הפונקציה min_path_sum().

את הטבלה ששמה, כרגיל, dp ניצור באמצעות 2 לולאות הרצות אחת בתוך השנייה. הערך ברירת המחדל בכל אחד מהתאים יהיה 0. למה 0? כי ידוע לנו מתנאי הבעיה שהערכים ב- grid, המייצגים את עלות המעבר, חייבים להיות חיוביים, ולכן 0 מייצג באופן הטוב ביותר תא שלא עברו דרכו.

def min_path_sum(grid):
    if not grid:
        return 0

    num_rows = len(grid)
    num_cols = len(grid[0])

    # Create a 2D array to store the minimum path sum for each cell
    dp = [[0] * num_cols for _ in range(num_rows)]

• הפונקציה min_path_sum() מקבלת רשת דו-ממדית של מספרים חיוביים grid כקלט.
• קודם כל בודקים אם ה-grid ריק. אם הוא ריק אז הפונקציה מחזירה 0 מכיוון שאין מסלול לחשב.
• קובעים את מספר השורות והעמודות ב-grid ומאחסנים במשתנים num_rows ו-num_cols.
• מאתחלים מערך דו-מימדי (מבנה דמוי טבלה) בשם dp (קיצור של תכנות דינמי) לאחסון סכום המסלול המינימלי עבור כל תא ב-grid. הממדים של מערך זה תואמים את הממדים של ה-grid, ואנו ממלאים אותו באפסים כערכים ברירת מחדל.

במסגרת האתחול נציב בתור ערך התא השמאלי העליון של dp את ערך התא השמאלי העליון של ה-grid:

# Initialize the top-left cell with the corresponding value from the grid
dp[0][0] = grid[0][0]

• מאתחלים את התא השמאלי העליון של מערך dp עם הערך של התא המתאים ברשת הקלט. תא זה מייצג את נקודת ההתחלה של המעבר שלנו (=traversal).

נוסיף את הקוד לחישוב השורה הראשונה של dp:

# Initialize the first row with cumulative sums
for j in range(1, num_cols):
    dp[0][j] = dp[0][j - 1] + grid[0][j]

• נאתחל את השורה הראשונה של מערך dp עם סכומים מצטברים. החל מהעמודה השנייה (אינדקס 1), נחשב את הסכום המצטבר על ידי הוספת הערך של התא משמאל במערך dp והערך של התא המתאים ברשת הקלט grid. שלב זה מבטיח שכל תא בשורה הראשונה יאחסן את סכום המסלול המינימלי הנדרש כדי להגיע לתא זה מהפינה השמאלית העליונה.

בדומה, נוסיף את הקוד לחישוב העמודה הראשונה של dp:

# Initialize the first column with cumulative sums
for i in range(1, num_rows):
    dp[i][0] = dp[i - 1][0] + grid[i][0]

• נאתחל את העמודה הראשונה של מערך dp עם סכומים מצטברים. החל מהשורה השנייה (אינדקס 1), נחשב את הסכום המצטבר על ידי הוספת ערך התא שמעליו במערך dp והערך של התא המתאים ב- grid. שלב זה מבטיח שכל תא בעמודה הראשונה יאחסן את סכום המסלול המינימלי הנדרש כדי להגיע אליו מהפינה השמאלית העליונה.

נחשב את המסלולים הקצרים ביותר עבור יתר תאי הטבלה dp:

# Calculate the minimum path sum for each cell
for i in range(1, num_rows):
    for j in range(1, num_cols):
        # Choose the minimum path sum from the cell above or the cell to the left
        dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]

• הקוד מחשב את סכום המסלול המינימלי עבור כל תא בחלק הנותר של הרשת (למעט השורה הראשונה והעמודה הראשונה). לשם כך, משתמשים בלולאה מקוננת שעוברת על כל התאים.

• עבור כל תא (i, j), מחשבים את סכום המסלול המינימלי על ידי בחירת הערך המינימלי בין התא מעליו (i-1, j) לבין התא משמאלו (i, j-1). לאחר מכן, מוסיפים את ערך התא המתאים (i, j) ב-grid לערך המינימלי המחושב. שלב זה מבטיח שנוכל למצוא את סכום המסלול המינימלי הנדרש להגעה לתא (i, j).

לבסוף, מחזירים את הערך המאוחסן בתא הימני תחתון של המערך dp בו מוחזק בסיום החישוב הערך המינימלי המחושב של סכום הדרכים המובילות מהפינה השמאלית העליונה לימנית התחתונה:

# The bottom-right cell contains the minimum path sum
return dp[num_rows - 1][num_cols - 1]

עכשיו הכל ביחד:

def min_path_sum(grid):
    if not grid:
        return 0

    num_rows = len(grid)
    num_cols = len(grid[0])

    # Create a 2D array to store the minimum path sum for each cell
    dp = [[0] * num_cols for _ in range(num_rows)]

    # Initialize the top-left cell with the corresponding value from the grid
    dp[0][0] = grid[0][0]

    # Initialize the first row with cumulative sums
    for j in range(1, num_cols):
        dp[0][j] = dp[0][j - 1] + grid[0][j]

    # Initialize the first column with cumulative sums
    for i in range(1, num_rows):
        dp[i][0] = dp[i - 1][0] + grid[i][0]

    # Calculate the minimum path sum for each cell
    for i in range(1, num_rows):
        for j in range(1, num_cols):
            # Choose the minimum path sum from the cell above or the cell to the left
            dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]
    
    # print(dp)
    
    # The bottom-right cell contains the minimum path sum
    return dp[num_rows - 1][num_cols - 1]

נבחן את הפונקציה:

grid = [
    [1, 3, 1],
    [1, 5, 1],
    [4, 2, 1]
]

print(min_path_sum(grid)) # 7

אוקיי. הפונקציה עובדת. האם היא יעילה?

סיבוכיות זמן: לפונקציה min_path_sum() סיבוכיות זמן של O(m * n), כאשר m הוא מספר השורות ו-n הוא מספר העמודות ב-grid. זאת מכיוון שיש צורך לעבור על כל תא ברשת פעם אחת בדיוק כאשר בכל תא מבצעים פעולות הדורשות זמן קבוע (חיבור והשוואה).

סיבוכיות מקום: סיבוכיות המקום היא גם O(m * n). האלמנט העיקרי הצורך מקום הוא טבלת התכנות הדינמי dp, שיש לה מידות של m שורות ו-n עמודות. טבלה זו מאחסנת את סכום המסלול המינימלי עבור כל תא, מה שהופך את סיבוכיות המקום לזהה למספר התאים ברשת.

אתגר: מציאת תת המחרוזת המשותפת הארוכה ביותר Longest common subsequence

נותנים לך שתי מחרוזות, ועליך למצוא את תת-המחרוזת המשותפת הארוכה ביותר הקיימת בשתיים.

Longest common subsequence (LCS)

תת-מחרוזת הוא רצף המופיע באותו סדר יחסי, אך לא בהכרח צמוד. במילים אחרות, עליך למצוא את הרצף הארוך ביותר של תווים המופיע בשני רצפי קלט נתונים.

נראה כמה דוגמאות:

longest_common_subsequence("ABCD", "BCD") # 3

• המחרוזת הארוכה ביותר המשותפת היא "BCD".

longest_common_subsequence("ABACBDAB", "BDCAB") # 4

• המחרוזת הארוכה ביותר המשותפת היא "BCAB" כי התווים לא חייבים לבוא אחד אחרי השני.

longest_common_subsequence("ABCDEF", "XYZ") # 0

• אין תווים משותפים.

אם אתה רוצה לנסות לפתור לבד, אתה מוזמן לנסות!

פתרון:

נחשוב על מקרה פשוט אותו ננסה לפענח. נאמר שיש לנו שני רצפים: "AXT" ו-"AYT". נשתמש בטבלה דו ממדית כדי להשוות ביניהם. הציר האופקי יהיה "AXT" והציר האנכי יהיה "AYT":

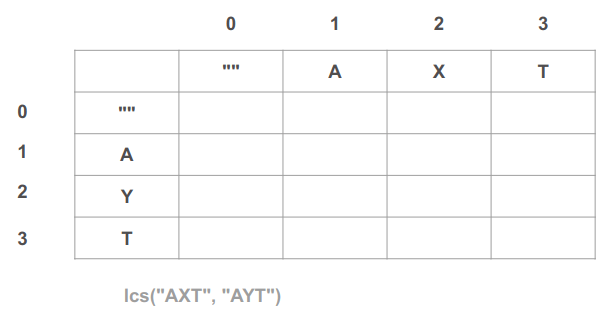
כל תא בטבלה הוא תת בעיה שצריך לפתור כדי לצבור את הפתרון המלא שיימצא בתא האחרון של הטבלה.

לדוגמה, התא (1, 1) מכיל את תת הבעיה של מציאת המחרוזת המשותפת בין "A" מהמחרוזת הראשונה ל-"A" מהמחרוזת השנייה:

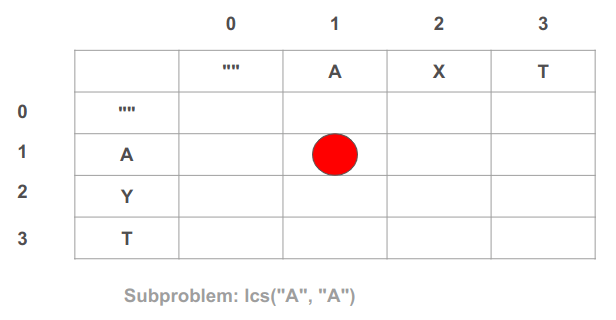
דוגמה נוספת היא התא (2, 1) אשר מכיל את תת הבעיה של מציאת המחרוזת המשותפת בין "AX" מהמחרוזת הראשונה בציר האופקי ל-"A" מהמחרוזת השנייה בציר האנכי:

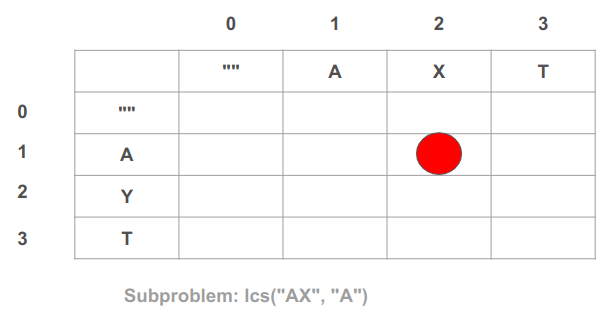
התא הימני התחתון - התא האחרון של הטבלה - הוא תת הבעיה שתסכם את כל הפתרונות אותם צברנו בתהליך כי היא משווה את שני הרצפים המלאים "AXT" ו-"AYT". את התוצאה המופיעה בתא זה תחזיר הפונקציה:

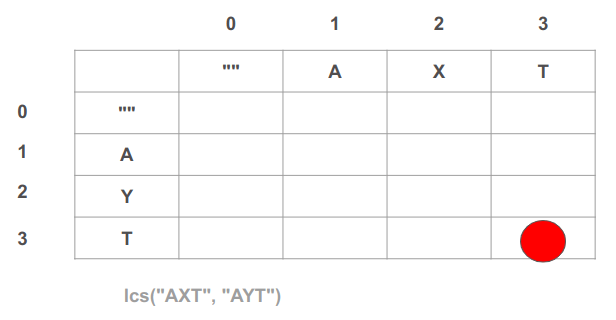
נאתחל את הטבלה כך שכל התאים בה יכילו אפסים:

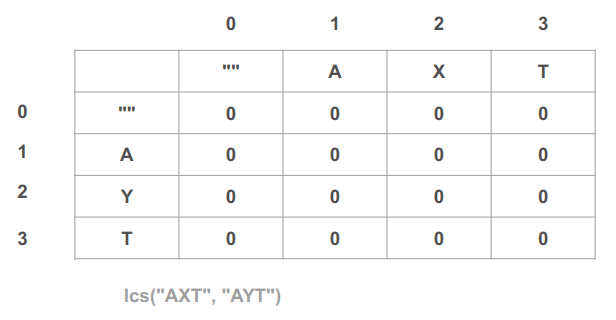
נסביר את הכללים:

• כל תא בטבלת התכנות הדינמי DP הוא תת בעיה שצריך לפתור כדי לצבור את הפתרון המלא אליו נגיע בתא האחרון של הטבלה.
• הטבלה כוללת מחרוזות ריקות ("") המהוות את מקרי הבסיס. משמאל ל-"AXT" בציר האופקי, ומעל ל-"AYT" בציר האנכי.
• הטבלה משמשת להשוואה לכן נמלא אותה באפסים כברירת מחדל כי אם נמצא התאמה נוסיף 1, ואם לא נמצא התאמה או שטרם טיפלנו יישאר 0.
• לא עוברים דרך השורה הראשונה וגם לא דרך העמודה הראשונה המייצגים מחרוזות ריקות ("") כי הם מקרי הבסיס שיהוו את העוגן ליתר החישובים.
• אם בתא מסויים מוצאים התאמה אז מוסיפים 1 למצב בו לא נמצאה התאמה זו המיוצג בתא הנמצא באלכסון צעד 1 למעלה וצעד 1 לשמאל כי תא זה מייצג את המצב שהיה לולא היה תו משותף (תיכף נסביר).
• לחילופין, אם לא מוצאים התאמה אז משווים איזה מהמצבים נותן את הערך הגבוה יותר כיוון שהוא מייצג את תת המחרוזת הארוכה יותר: מצב ללא התו הנוכחי בציר האופקי או לחלופין בציר האנכי, ומציבים ערך זה בתור ערכו של התא.

עברנו על הכללים ממש מהר. נספק פירוט ונדגים.

אין צורך לעדכן את התאים של המחרוזות הריקות שהוספנו משמאל ל-"AXT" בציר האופקי, ומעל ל-"AYT" בציר האנכי כי הוספנו אותם כמקרי בסיס כדי שנוכל להיעזר בהם כעוגן לחישובים.

בתא (1, 1) אנחנו פותרים את תת הבעיה מהי תת המחרוזת המשותפת בין "A" מהמחרוזת הראשונה ל-"A" מהמחרוזת השנייה:

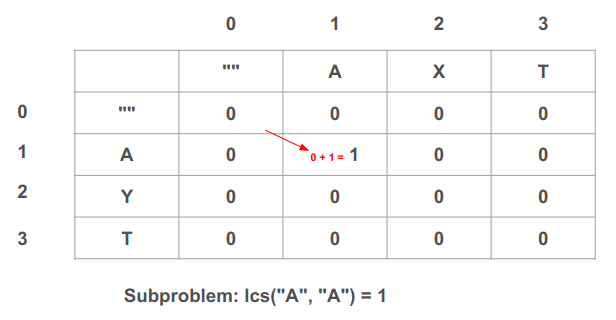
• כיוון ששתי תת המחרוזות הבאות משני הקלטים ערכם הוא "A" והם זהות נוסיף 1 למצב לולא הייתה התאמה. לשם כך נוסיף 1 לערך הרשום בתא משמאל למעלה, שהוא 0 במקרה זה, ולפיכך נרשום 1 בתא הנוכחי ע"פ 0 + 1 = 1.
• למה אנחנו מוסיפים 1 לערך התא משמאל למעלה? כי התא משמאל למעלה מכיל את כמות ההתאמות הנצברת עבור המצב ללא התו המשותף שמצאנו זה עתה. צריך להבין שהתו המשותף נמצא בשתי המחרוזות, האופקית וגם האנכית. נעים לשמאל כדי לדמות את המצב בו התו "A" של המחרוזת האופקית לא היה קיים. עולים למעלה כדי לדמות את המצב בו התו "A" של המחרוזת האנכית לא היה קיים. בסה"כ נעים למעלה ושמאלה כדי לדמות את המצב בו התו המשותף בשתי המחרוזות לא היה קיים, לוקחים את הערך הרשום בתא זה, ומוסיפים לו 1 כי מצאנו התאמה.

נעבור ימינה לתא הבא בשורה (1, 2) בו פותרים את תת הבעיה מהי תת המחרוזת המשותפת בין "AX" מהמחרוזת הראשונה ל-"A" מהמחרוזת השנייה:

• "X" שונה מ-"A", ולכן אנחנו צריכים לקחת את הערך הגבוה ביותר מהמצב הקודם. אבל איזה מצב קודם? אין אחד, יש שניים:

1. אחד כשמורידים את "X" בציר האופקי.
2. שני כשמורידים את "A" בציר האנכי.

בשביל מצב #1 לוקחים את ערך התא משמאל השווה ל-1. בשביל המצב #2 לוקחים את ערך התא מלמעלה השווה ל-0. משווים בין שני הערכים ולוקחים את הכי גבוה כי המטרה היא לבחור את המצב המייצג את המחרוזת המשותפת הארוכה ביותר: MAX(1, 0) = 1. ולכן נעדכן את ערך התא הנוכחי שיהיה 1.

נעבור ימינה לתא הבא בשורה (1, 3) בו פותרים את הבעיה מהי תת המחרוזת המשותפת בין "AXT" מהמחרוזת הראשונה ל-"A" מהמחרוזת השנייה:

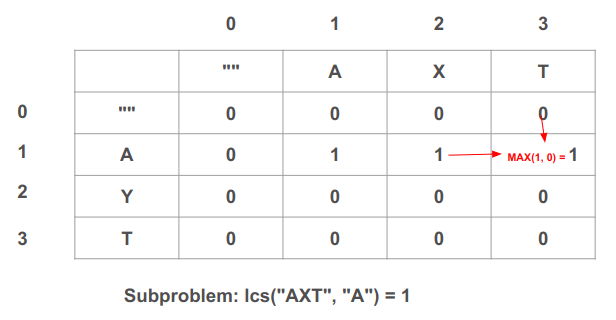
• "T" שונה מ-"A", ולכן אנחנו צריכים לקחת את הערך הגבוה ביותר מבין שני המצבים הקודמים. MAX(1, 0) = 1 אז נעדכן את ערך התא כדי שיהיה 1.

נרד לשורה הבאה.

בתא (1, 2) נפתור את תת הבעיה מהי תת המחרוזת המשותפת בין "A" מהמחרוזת הראשונה ל-"AY" מהמחרוזת השנייה:

• כיוון ש-"A" שונה מ-"Y" ניקח את הערך הגבוה בין השכנים משמאל ומלמעלה: MAX(0, 1) = 1. נעדכן בהתאם את ערך התא שיהיה 1.

נעבור ימינה לתא (2, 2) בו נפתור את תת הבעיה מהי תת המחרוזת המשותפת בין "AX" מהמחרוזת הראשונה ל-"AY" מהשנייה:

• כיוון ש-"X" שונה מ-"Y" ניקח את הערך הגבוה בין השכנים משמאל ומלמעלה: MAX(1, 1) = 1. נעדכן בהתאם את ערך התא ל- 1.

נעבור שוב ימינה, לקצה השורה, לתא (3, 2) בו נפתור את תת הבעיה מהי תת המחרוזת המשותפת בין "AXT" מהמחרוזת הראשונה ו-"AY" מהמחרוזת השנייה:

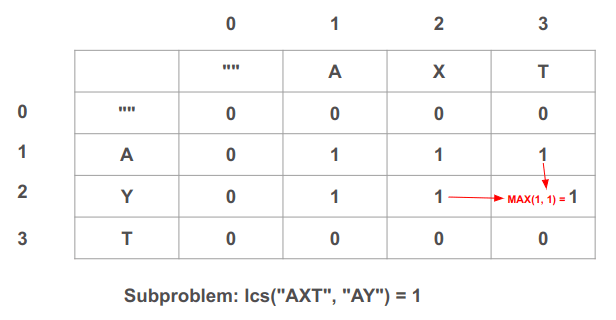
• כיוון ש-"T" שונה מ-"Y" ניקח את הערך הגבוה בין השכנים משמאל ומלמעלה: MAX(1, 1) = 1. נעדכן בהתאם את ערך התא כדי שיהיה 1.

נמשיך את המעבר ונרד לשורה האחרונה של הטבלה.

בתא (3, 1) נפתור את תת הבעיה מהי תת המחרוזת המשותפת בין "A" מהמחרוזת הראשונה ל-"AYT" מהמחרוזת השנייה:

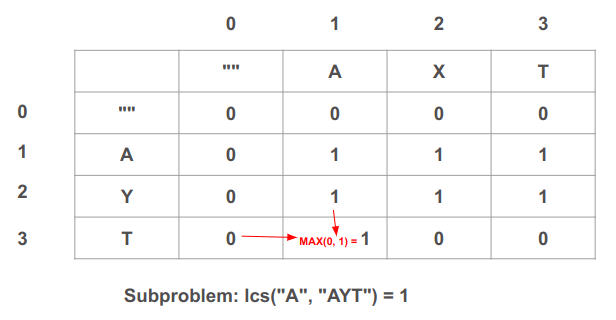
• כיוון ש-"A" שונה מ-"T" ניקח את הערך הגבוה בין השכנים משמאל ומלמעלה: MAX(0, 1) = 1. נעדכן בהתאם את ערך התא כדי שיהיה 1.

נעבור ימינה. לתא (2, 3) בו נפתור את תת הבעיה מהו אורך תת המחרוזת המשותפת בין "AX" מהמחרוזת הראשונה ל-"AYT" מהמחרוזת השנייה:

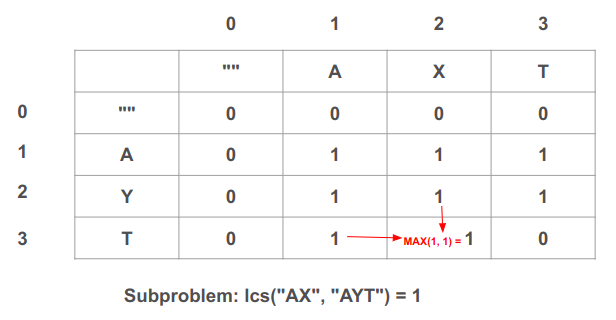
• כיוון ש-"X" שונה מ-"T" ניקח את הערך הגבוה בין השכנים משמאל ומלמעלה: MAX(1, 1) = 1. נעדכן בהתאם את ערך התא כדי שיהיה 1.

נעבור שוב ימינה לתא האחרון של הטבלה בו נפתור את תת הבעיה מהי תת המחרוזת המשותפת בין "AXT" ל-"AYT":

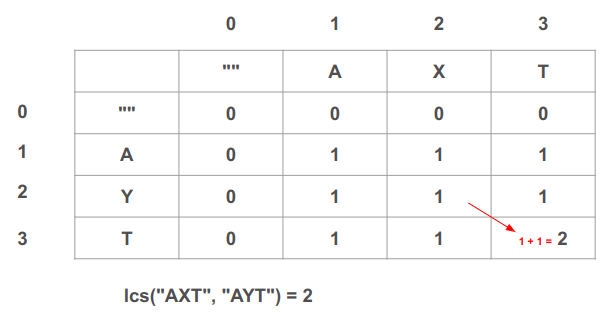
• כיוון ששתי תת המחרוזות "T" ו-"T" זהות נוסיף 1 למצב לולא הייתה התאמה. לשם כך נוסיף 1 לערך הרשום בתא משמאל למעלה, שהוא 1 במקרה זה, ולפיכך נרשום 2 בתא הנוכחי ע"פ 1 + 1 = 2.

בסופו של דבר, צריך להחזיר את הערך בתא האחרון היות והוא הערך הצבור של תתי הפתרונות עבור כל המצבים.

אחרי שהבנו נכתוב את קוד הפונקציה למציאת תת המחרוזת המשותפת הארוכה ביותר:

def longest_common_subsequence(s1, s2):

נוסיף לפונקציה את הקוד ליצירת הטבלה הדו מימדית שממדיה תואמים את אורך המחרוזות כאשר כל אחד מהתאים מכיל ערך ברירת מחדל 0:

m, n = len(s1), len(s2)

# Create a 2D table to store the length of Longest Common Subsequence (LCS)
dp = [[0] * (n + 1) for _ in range(m + 1)]

נעבור על התאים אחד אחד בתוך זוג לולאות מקוננות הרצות כל אחת מהעמדה הבאה אחרי הראשונה ועד לסוף המחרוזת (העמדה הראשונה שמורה למחרוזת ריקה):

# Fill in the table using dynamic programming
for i in range(1, m + 1):
    for j in range(1, n + 1):

בתוך הלולאות נבדוק אם יש התאמה בתווים. במידה וישנה התאמה נוסיף 1 לערך התא אשר נמצא על האלכסון המצביע לכיוון למעלה ושמאל:

# If the current characters match, extend the LCS
if s1[i - 1] == s2[j - 1]:
    dp[i][j] = dp[i - 1][j - 1] + 1

אם התווים שונים, ניקח את ערך המקסימום מבין שתי האפשרויות שלא כוללות את התווים בתא הנוכחי:

# If they don't match, take the maximum of the LCS without either character
else:
    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])

לבסוף, הפונקציה מחזירה את הערך בתא הימני התחתון של הטבלה המכיל את אורך תת המחרוזת הארוכה ביותר שנצברה בתהליך:

# The value in the bottom-right cell of the table represents the length of LCS
return dp[m][n]

עכשיו הכל ביחד:

def longest_common_subsequence(s1, s2):
    m, n = len(s1), len(s2)


    # Create a 2D table to store the length of Longest Common Subsequence (LCS)
    dp = [[0] * (n + 1) for _ in range(m + 1)]


    # Fill in the table using dynamic programming
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            # If the current characters match, extend the LCS
            if s1[i - 1] == s2[j - 1]:
                dp[i][j] = dp[i - 1][j - 1] + 1
            # If they don't match, take the maximum of the LCS without either character
            else:
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])


    # The value in the bottom-right cell of the table represents the length of LCS
    return dp[m][n]

נבדוק את הפונקציה שכתבנו:

print(longest_common_subsequence("AXT", "AYT")) # 2 (LCS: "AT")
print(longest_common_subsequence("AXYWZ", "WYXWZ")) # 3 (LCS: "XWZ")
print(longest_common_subsequence("ab", "ab")) # 2 (LCS: "ab")
print(longest_common_subsequence("xyz", "y")) # 1 (LCS: "y")
print(longest_common_subsequence("y", "xyz")) # 1 (LCS: "ga")
print(longest_common_subsequence("m", "xyz")) # 0 (Nothing in common)
print(longest_common_subsequence("mgba", "ga")) # 2 (LCS: "ga")
print(longest_common_subsequence("AGGTAB", "GXTXAYB")) # 4
print(longest_common_subsequence("ABCDEF", "XYZ")) # 0 (No common characters)
print(longest_common_subsequence("ABCD", "BCD")) # 3 (The entire "BCD" is a common subsequence)
print(longest_common_subsequence("AGGTAB", "GXTXAYB")) # 4 (LCS: "GTAB")
print(longest_common_subsequence("ABACBDAB", "BDCAB")) # 4 (LCS: "BCAB")
print(longest_common_subsequence("XMJYAUZ", "MZJAWXU")) # 4 (LCS: "MJAU")
print(longest_common_subsequence("aaaaaa", "aa")) # 2 (LCS: "aa")
print(longest_common_subsequence("abcd", "")) # 0 (One of the strings is empty)
print(longest_common_subsequence("", "xyz")) # 0 (One of the strings is empty)
print(longest_common_subsequence("", "")) # 0 (Both strings are empty)

הפונקציה אכן עובדת אז הגיע הזמן להעריך את יעילותה.

סיבוכיות המקום (Space Complexity):סיבוכיות המקום של הפונקציה longest_common_subsequence() היא O(m * n). זו תוצאה ישירה של שימוש בטבלת תכנות דינמית `dp`, שממדיה הם`(m+1)` שורות ו-`(n+1)` עמודות. הטבלה מאחסנת את אורך המחרוזת המשותפת הארוכה ביותר עבור כל תא בטבלה. כך, סיבוכיות המקום תלויה בגודל הקלט (=אורך 2 המחרוזות).

סיבוכיות זמן (Time Complexity): סיבוכיות זמן של הפונקציה longest_common_subsequence() היא O(m * n). הזמן הדרוש לחישוב תלוי בממדי המחרוזות אותם מקבלת הפונקציה כקלט, כאשר `n` הוא אורך המחרוזת הראשונה ו-`m` הוא אורך המחרוזת השנייה. בלולאות המקוננות, עוברים על כל תא בטבלה פעם אחת בדיוק. בכל תא, מבצעים פעולות חיבור והשוואה הדורשת זמן ביצוע קבוע.

אתגר: בעיית הקיטבג - להכניס או לא להכניס לשק knapsack 0/1

אתגר תכנות קלאסי שכדאי לפתור אותו באמצעות תכנות דינאמי הוא knapsack 0/1 אותו הסברתי בפירוט רב במדריך "פתרון בעיית הקיטבג knapsack באמצעות תכנות דינאמי". אם הגעת עד לפה אז כדאי לך להקדיש זמן לקריאתו גם כדי לחזק את מה שלמדנו במדריך וגם כדי ללמוד דברים נוספים על תכנות דינאמי.

סיכום

במדריך הזה, חווינו איך עובד תכנות דינמי בפועל באמצעות פתרון שישה אתגרים תכנותיים. בכל הפתרונות, עבדנו על פי גישת "מלמטה למעלה", העדיפה כאשר מתמודדים עם בעיות שבהן קריאות רקורסיביות רבות עלולות לגרום להצפת זיכרון Stack Overflow אם משתמשים בגישת "מלמעלה למטה".

המשותף לפתרונות אלו הוא שימוש ב-2 רעיונות המשותפים לכולם: (1) שבירה לבעיות משנה קלות לפתרון (2) צבירת הפתרונות במבני נתונים המשמשים כ-"קאש". במדריך, קראנו למבני הנתונים האלו "טבלה" כאשר לאחר שסיימנו לפתור כל אחת מהבעיות הקטנות, משכנו את הפתרון מסופה של הטבלה.

מה שכדאי לזכור מהמדריך הזה הוא את צמד הרעיונות: (1) שבירה לתתי בעיות ו-(2) צבירה בקאש. שימוש בכל רעיון בנפרד, ושילוב בין הרעיונות יכול לתרום רבות ליכולות של כל מתכנת, בהקשר של פתרון בעיות בתחום התכנות הדינאמי, ולא רק בו.

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

רקורסיה בפייתון - כל מה שרצית לדעת ועוד כמה דברים חשובים

פתרון בעיות אופטימיזיציה באמצעות אלגוריתם חמדן

פתרון בעיית הקיטבג knapsack באמצעות תכנות דינמי

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים