אלגוריתם דייקסטרה Dijkstra למציאת הנתיב הקצר ביותר בגרף ממושקל

מטרת אלגוריתם דייקסטרה Dijkstra היא למצוא את הנתיב הקצר ביותר בין צומת התחלה לכל יתר הצמתים בגרף מכוון ממושקל weighted directed graph.

לדוגמה, הגרף הפשוט הבא:

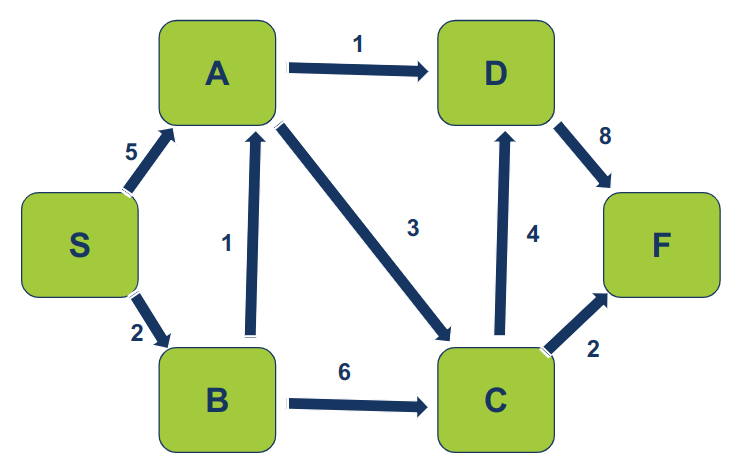
המטרה היא למצוא את הנתיב הקצר ביותר מצומת "S" לכל יתר הצמתים.

הרצת האלגוריתם תפיק מידע אותו ניתן לסכם בטבלה:

בעמודה הימנית המרחק הקצר ביותר בין כל צומת Node לצומת ההתחלה (S).

לדוגמה, בשורה הראשונה, המרחק של הצומת "S" (start) לעצמו הוא 0.

המרחק בין הצמתים S ו- B הוא 2:

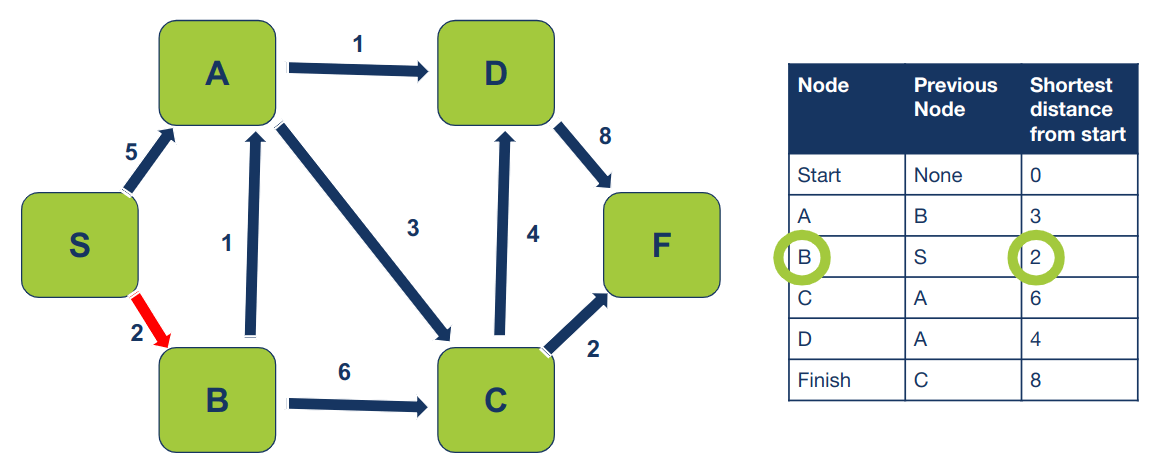
והמרחק הקצר ביותר בין הצמתים S ו-A הוא 3:

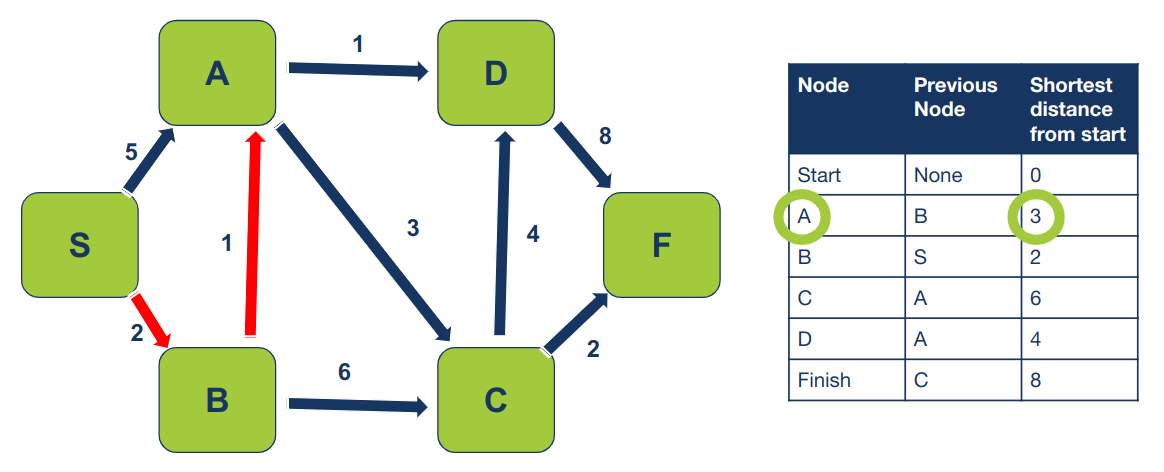
העמודה האמצעית מציגה את הצומת הקודם לנוכחי כשמחשבים את המסלול הקצר ביותר מצומת ההתחלה. לדוגמה, ל-A הכי קצר להגיע מ- B (ולא ישירות מ-S):

ל-F הכי קצר להגיע מ-C:

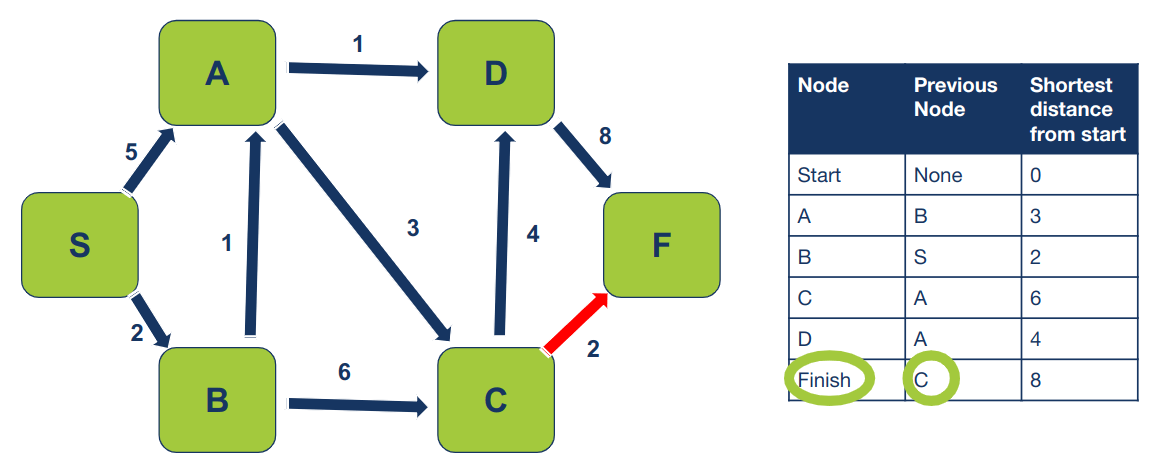
אנחנו יכולים להשתמש במידע על הצומת הקודם לנוכחי כדי לשחזר את הנתיב הקצר ביותר מ- F ל-S, מסוף הנתיב לראשיתו:

הצומת הבא לפני F הוא C:

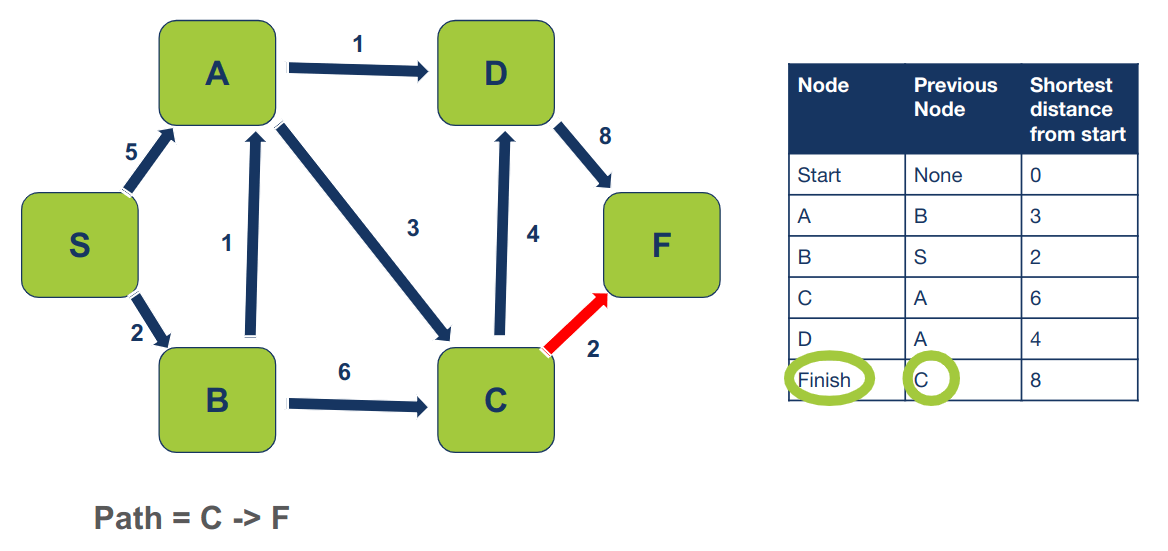
• Path = C -> F

הצומת הקודם ל-C הוא A:

• Path = A -> C -> F

הקודם ל-A הוא B:

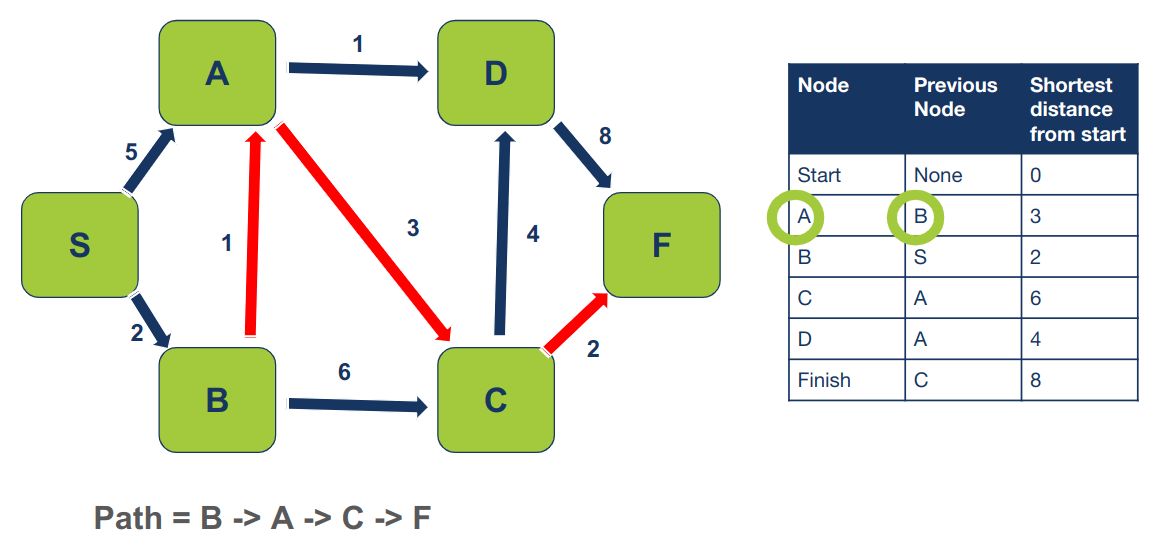
• Path = B -> A -> C -> F

הקודם ל-B הוא S:

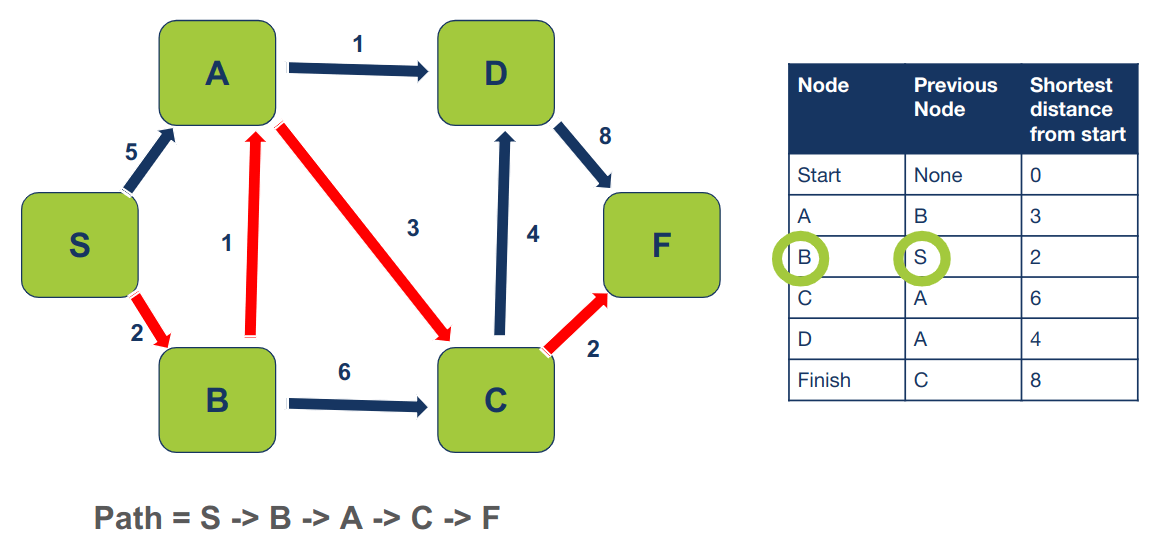
מה שמאפשר לנו לשחזר את הנתיב הקצר ביותר המוביל מ-S ל-F שהוא:

• Path = S -> B -> A -> C -> F

נתיב שאורכו 8 כפי שניתן להיווכח מהטבלה:

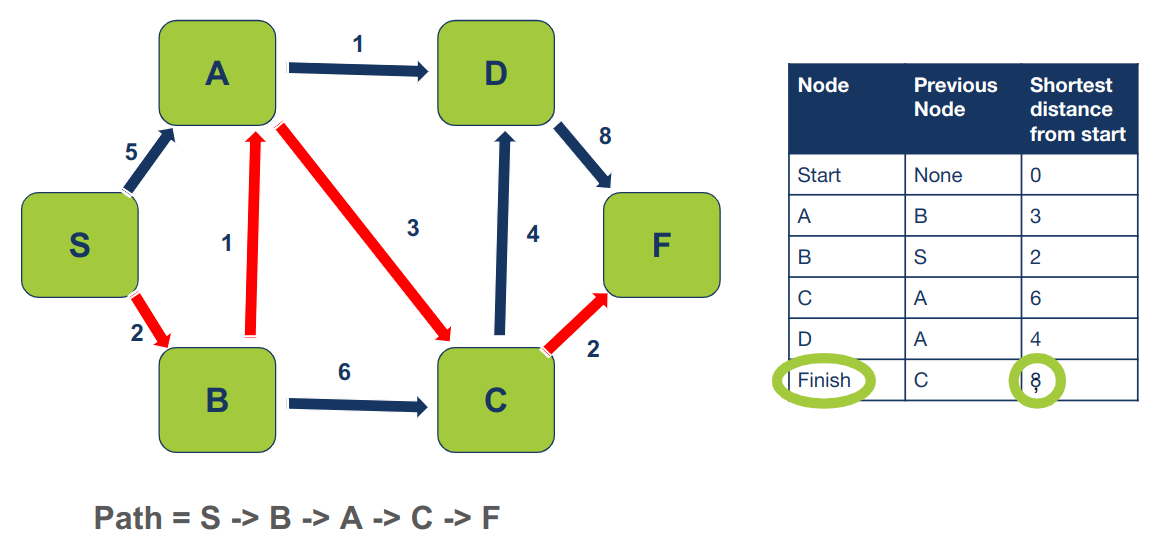
לאותה מסקנה על אורך הנתיב הקצר ביותר שבין צומת ההתחלה והסיום ניתן להגיע על ידי חיבור המשקלים של הקשתות edges המחברות בין הצמתים:

Path        distance
S -> B       2
B -> A       1
A -> C       3
C -> F       2
================
S -> F       8

איך עובד אלגוריתם דייקסטרה למציאת הנתיב הקצר ביותר של גרף מכוון וממושקל?

אלגוריתם דייקסטרה מתחיל מהגדרת המרחקים בין כל צומת לצומת ההתחלה כאשר כברירת מחדל המרחק מצומת ההתחלה S לעצמו הוא 0 בעוד המרחק מ-S לכל צומת אחר הוא אינסוף (∞).

• עוד דבר שאנו יודעים בוודאות הוא שאין צומת הבא לפני צומת המוצא S. בהתאם, סימנו את הצומת הקודם ל-S כ-None.

נתחיל מלבקר את הצומת שיש לו את המרחק הקצר ביותר מצומת ההתחלה (במקרה שלנו, זה S שיש לו מרחק של 0 מעצמו). בשלב זה, נבקר את השכנים של S בהם טרם ביקרנו, ונחשב את המרחק מנקודת ההתחלה לכל שכן. השכנים של S הם A ו-B:

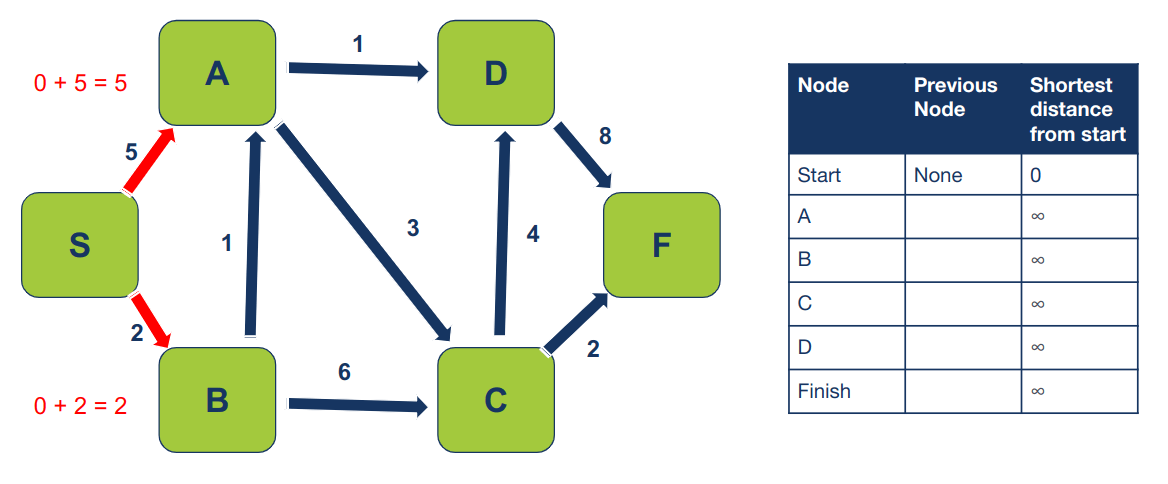
במידה והמרחק המחושב הוא קצר יותר נעדכן את הטבלה. במקרה שלנו המרחק ל-A הוא 5 והוא קצר יותר מ- ∞, וגם המרחק ל-B שהוא 2 הוא קצר יותר מ- ∞. נעדכן את הטבלה בהתאם:

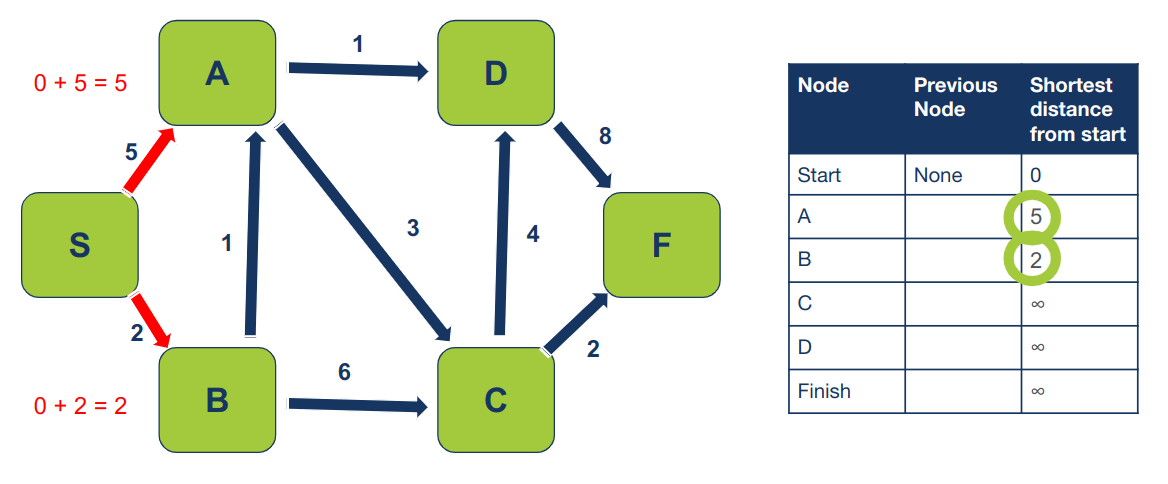
כיוון שהגענו ל-A ו-B מ- S נעדכן גם את המידע הזה בטבלה:

אחרי שביקרנו בכל השכנים, נסמן את S כמי שביקרנו בו כדי שלא נוכל לבקרו פעם נוסף.

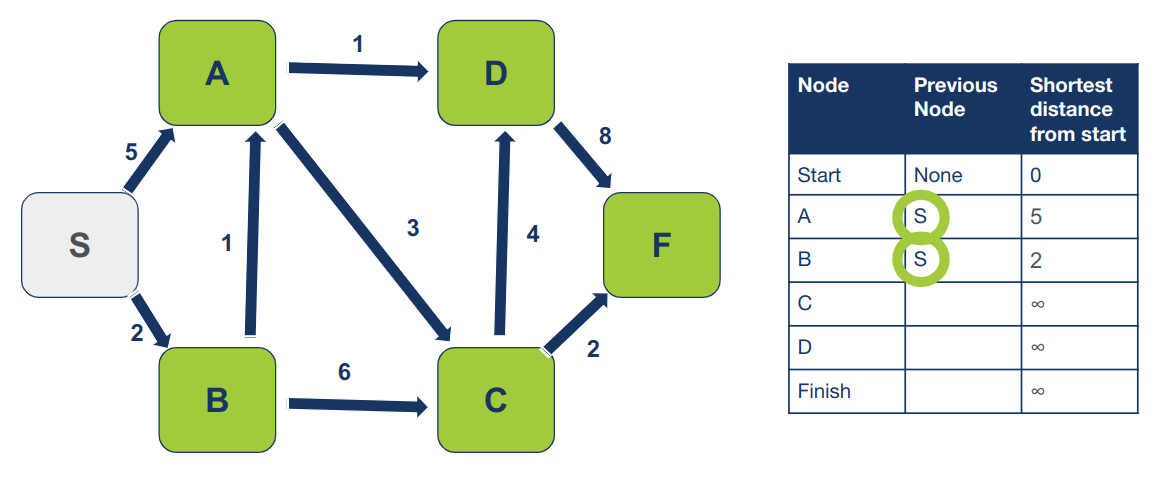
נחזור על התהליך.

נבקר את הצומת בו טרם ביקרנו שיש לו את המרחק הקצר ביותר מצומת ההתחלה. במקרה זה, הצומת הוא B. נבחן את שכניו בהם טרם ביקרנו (A ו- C):

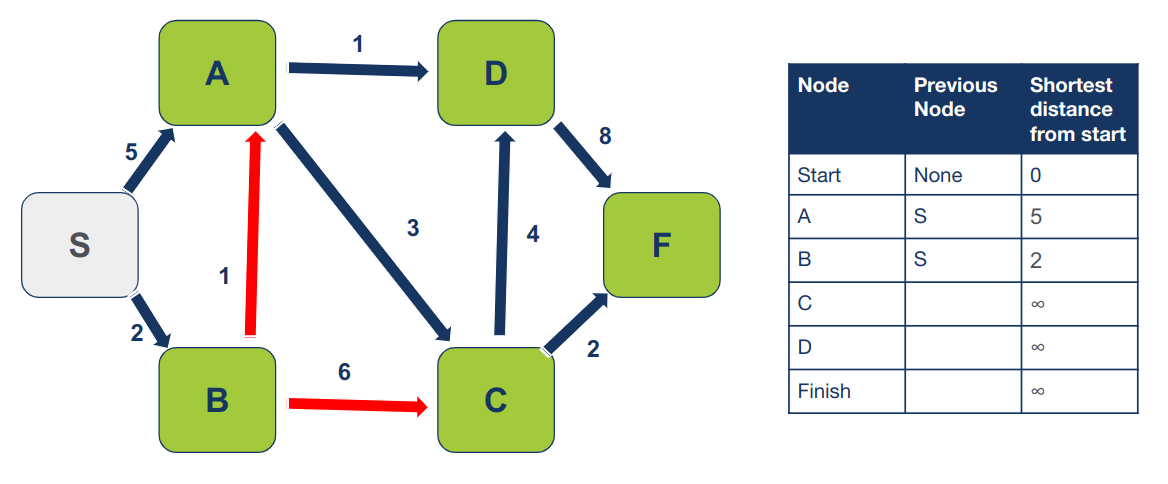
נחשב את המרחק של כל שכן מצומת ההתחלה:

S -> A = 2 + 1 = 3
S -> C = 2 + 6 = 8

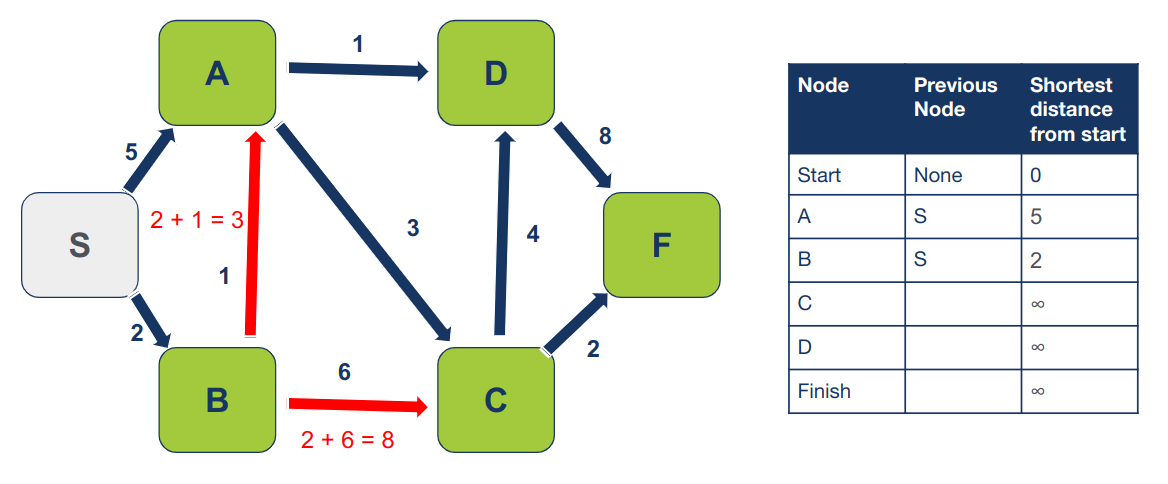
כיוון שהמרחק המחושב של A (3) הוא קצר יותר מהמרחק בטבלה (5) נעדכן את המרחק של A בטבלה, וגם את הצומת הקודם כי עכשיו קצר לנו יותר להגיע ל-A דרך B מאשר ישירות מ-S:

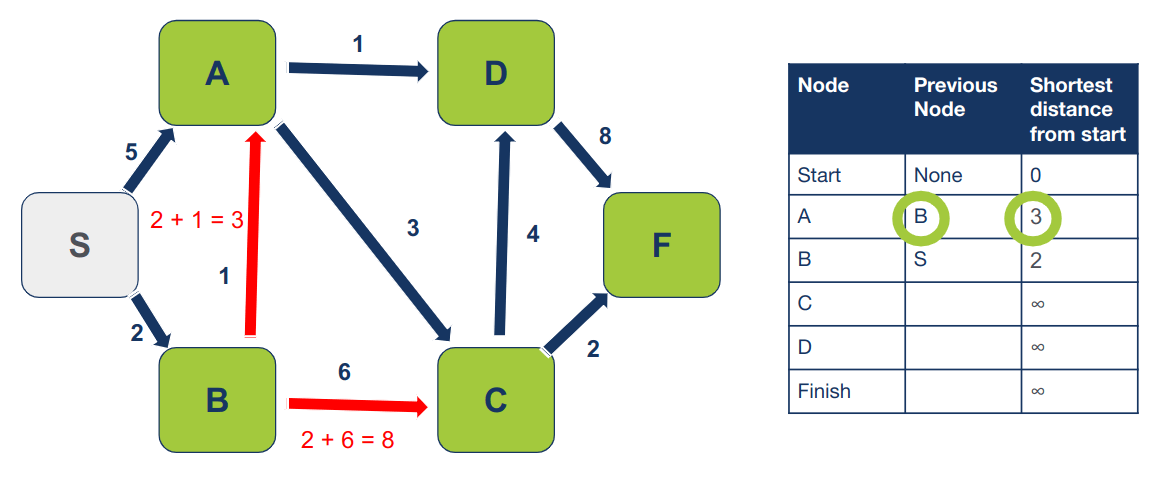
כיוון שהמרחק המחושב של C (8) הוא קצר יותר מהמרחק בטבלה (∞) נעדכן את המרחק של C בטבלה, וגם את הצומת הקודם כיוון שהגענו ל-C דרך B:

כיוון שסיימנו לסרוק את כל השכנים של B, אנחנו יכולים לסמן אותו כמי שביקרנו בו כדי שלא נחזור לבקר בו יותר:

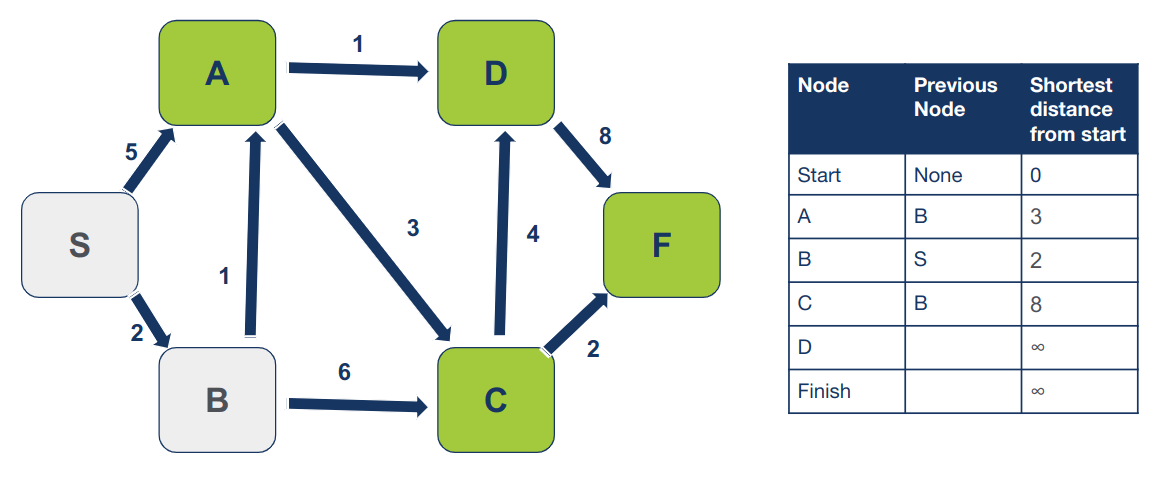
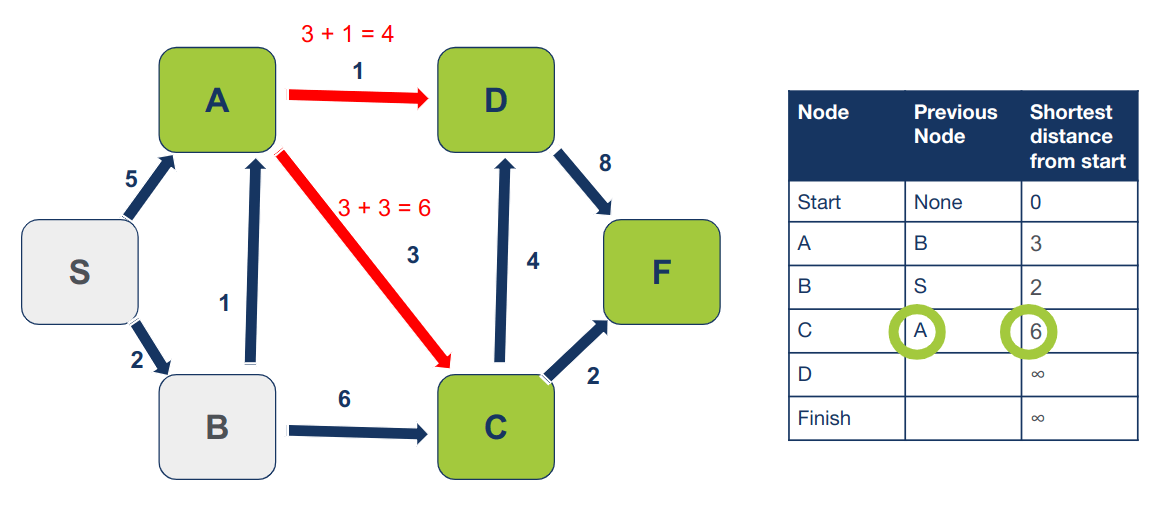
נחזור על התהליך עבור הצומת בו טרם ביקרנו שיש לו את המרחק הקצר ביותר מצומת ההתחלה. הפעם זה A ששכניו, בהם טרם ביקרנו, הם D ו- C.

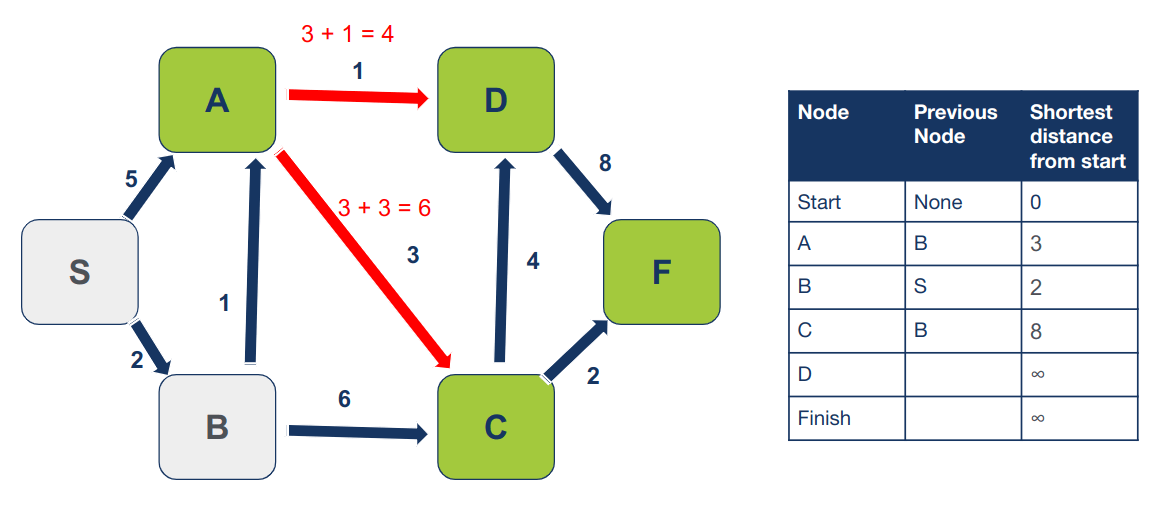
נחשב את המרחק של C ו- D מצומת ההתחלה:

S -> C = 6
S -> D = 4

כיוון שהמרחק של C המופיע בטבלה הוא 8 והוא ארוך יותר מהמרחק המחושב כשעוברים דרך A שהוא 6, נעדכן את המרחק של C בטבלה וגם את הצומת הקודם:

המרחק המחושב של D אף הוא קצר יותר מהמופיע בטבלה על כן נעדכן את המרחק ואת הצומת הקודם:

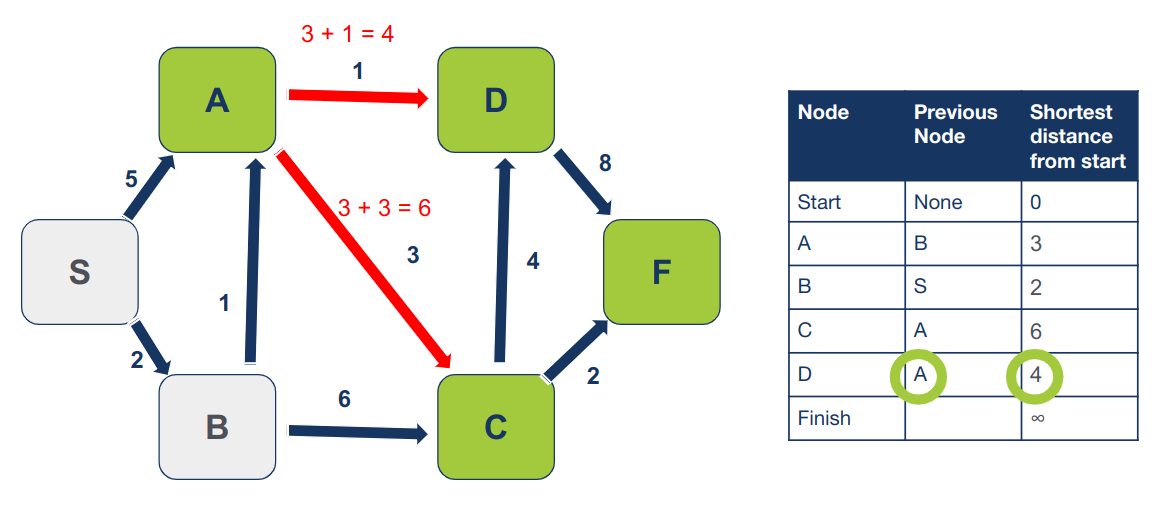
נסמן את A כמי שביקרנו בו. לא נחזור אליו יותר.

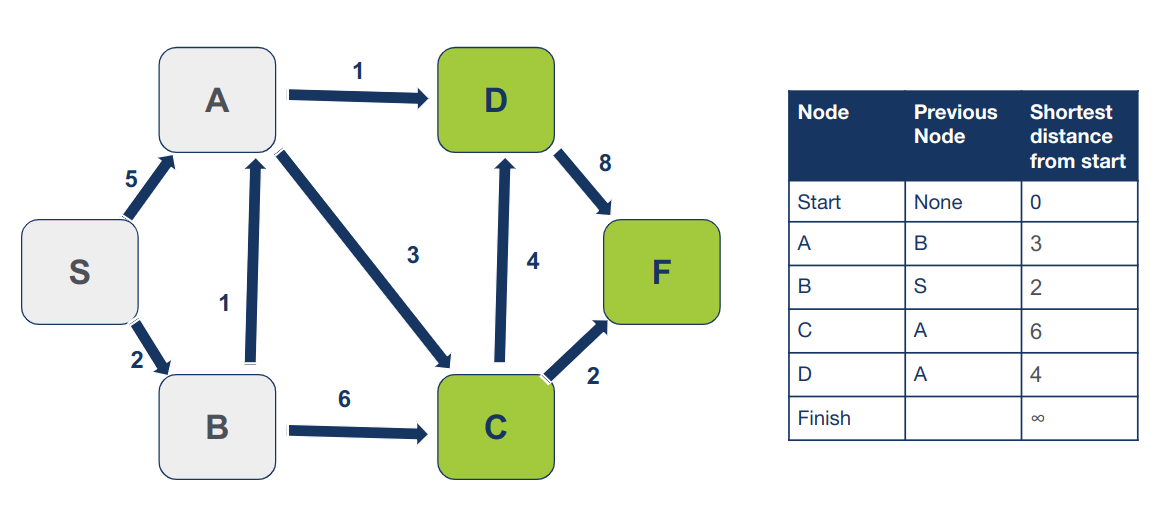
נחזור על התהליך עבור D שהוא הצומת הבא שטרם ביקרנו בו הנמצא במרחק הקצר ביותר מצומת המוצא. השכן היחיד של D הוא F. נחשב את המרחק של F מצומת ההתחלה `4 + 8 = 12`. המרחק המחושב קטן יותר מהערך המופיע בטבלה (∞). ע"כ נעדכן את המרחק של הצומת F ואת הצומת המוביל אליו:

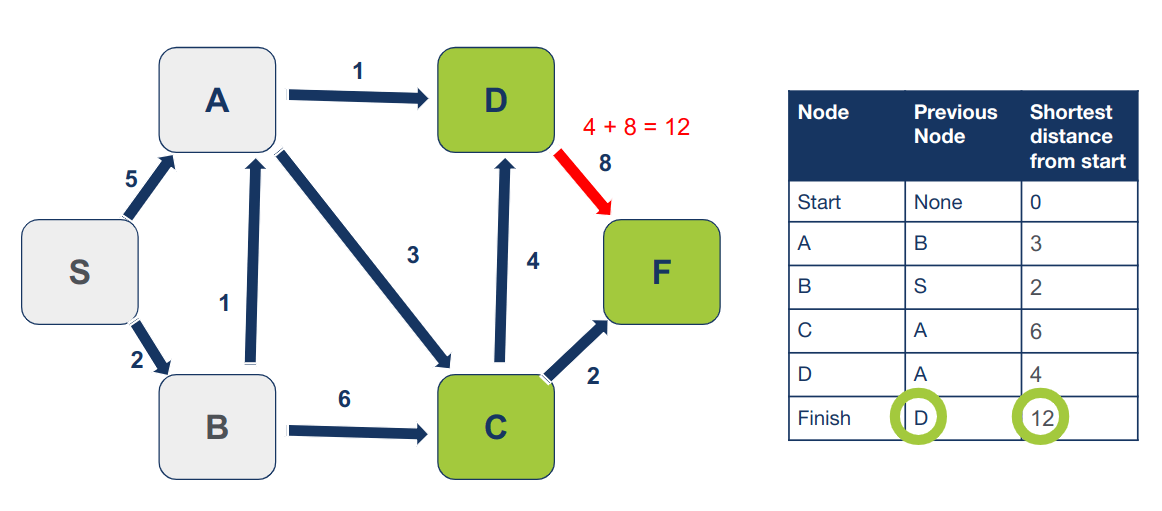
נסמן את D כמי שביקרנו בו. לא נחזור אליו יותר.

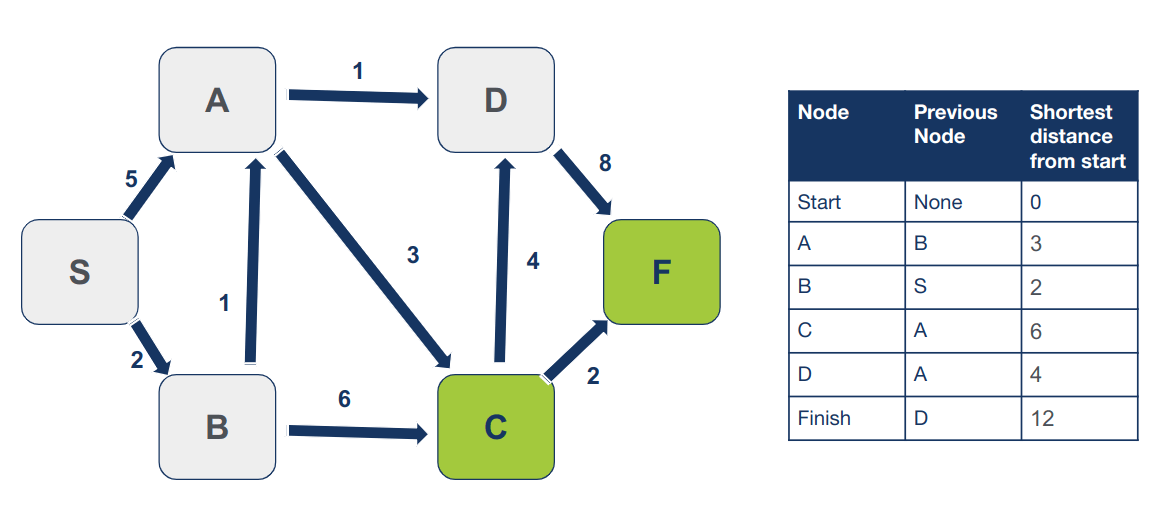
נחזור על התהליך עבור C שהוא הצומת הנמצא במרחק הקצר ביותר מצומת ההתחלה בו טרם ביקרנו. השכן היחיד של C הוא F. נחשב את המרחק של F מצומת ההתחלה כאשר מגיעים דרך C :

6 + 2 = 8

המרחק המחושב (8) קצר יותר מהערך בטבלה (12). ע"כ נעדכן את המרחק של F מצומת המוצא ואת ההורה:

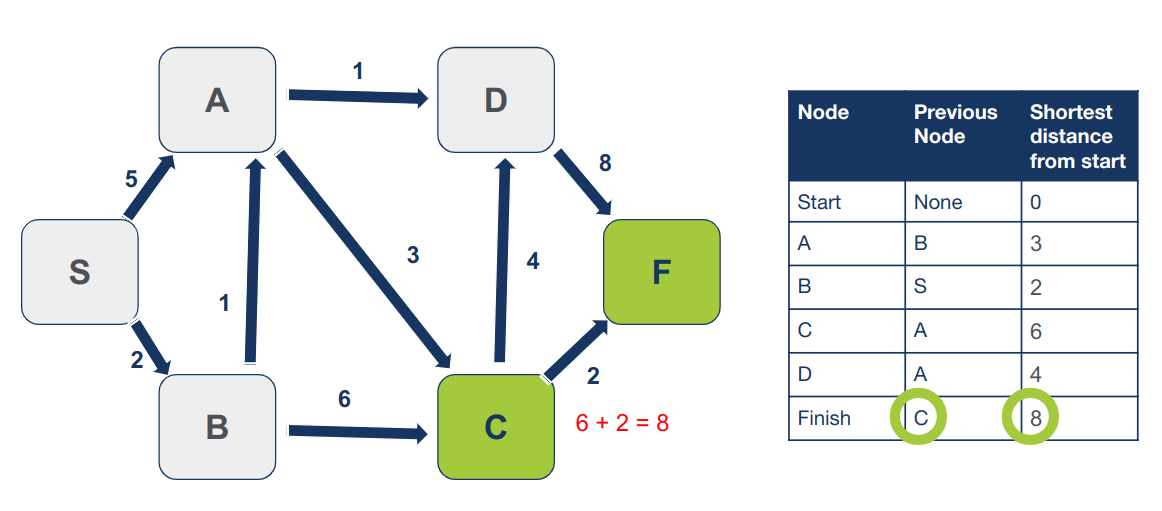
נסמן את C כמי שביקרנו בו. לא נחזור אליו יותר.

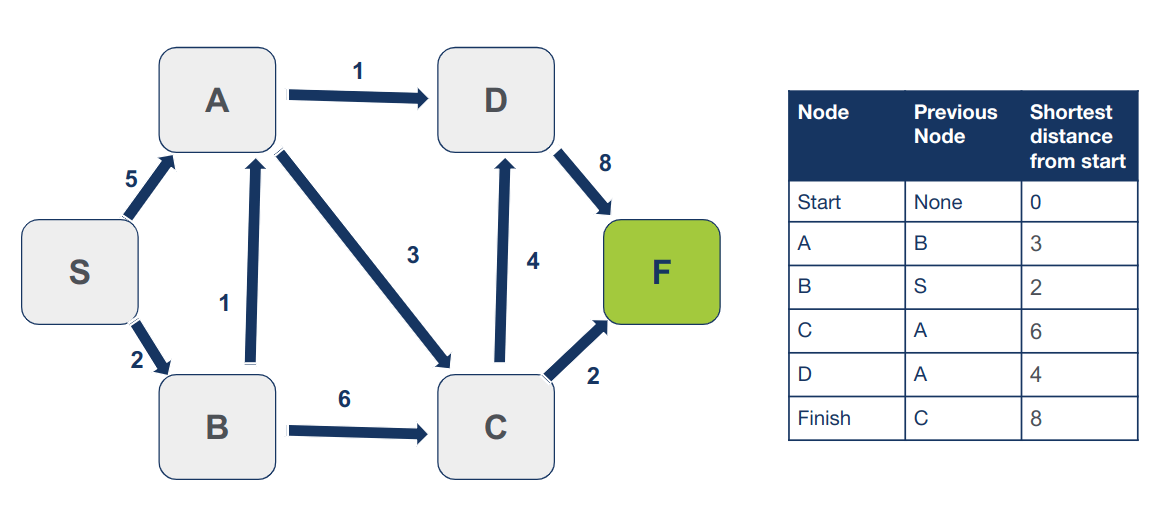
הצומת האחרון בו טרם ביקרנו הוא F. אבל מכיוון שאין לו שכנים נסמן אותו כמי שביקרנו בו.

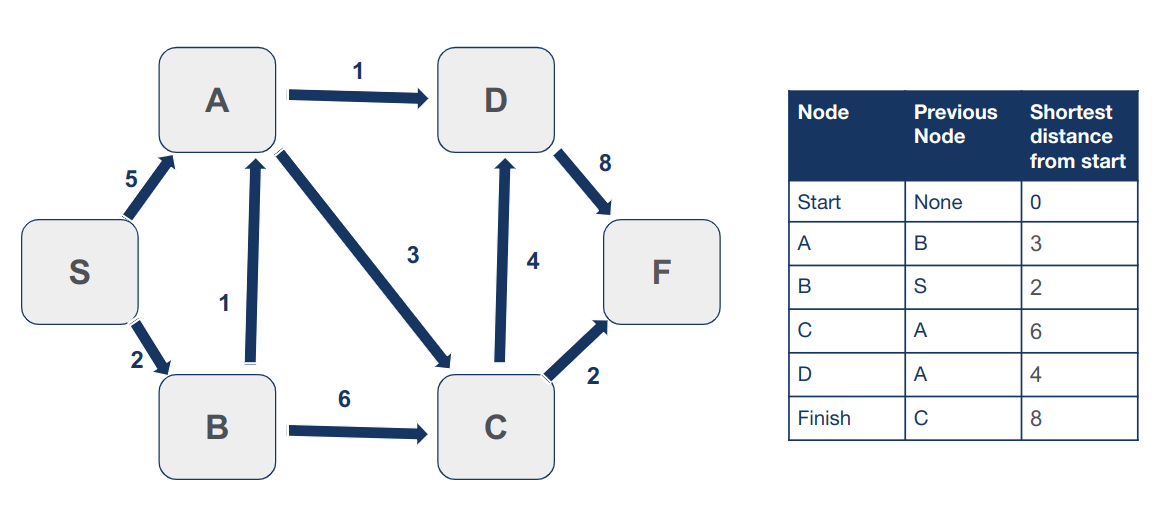
אין יותר צמתים שלא ביקרנו בהם ועל כן סיימנו להריץ את האלגוריתם. כל המידע לו אנו זקוקים מסוכם עכשיו בטבלה.

נסכם את מה שעשינו באמצעות אלגוריתם:

• נגדיר את מרחקם של כל הצמתים מצומת ההתחלה כ-∞. כאשר המרחק של צומת ההתחלה מעצמו הוא 0.

• נריץ את האלגוריתם בתוך לולאה עד לביקור בכל הצמתים. בכל פעם שהלולאה רצה:

  1. נבקר את הצומת שטרם ביקרנו בו שיש לו את המרחק הקצר ביותר מצומת המוצא
  2. נבקר את שכניו של הצומת בהם טרם ביקרנו
  3. נחשב את המרחק של כל שכן מצומת ההתחלה
  4. אם המרחק המחושב קצר יותר, נעדכן את המרחק ואת הצומת הקודם לו
  5. נגדיר את הצומת כמי שביקרנו בו

אלגוריתם דייקסטרה נחשב לאלגוריתם חמדן וזה בגלל שבכל שלב מבקרים בצומת שיש לו את המרחק הקצר ביותר מצומת המוצא כי ההנחה היא שיש לקחת את האפשרות הטובה ביותר הנראית לעין בכל שלב בלי לקחת בחשבון את התוצאה הסופית (אורך הדרך כולה) ובלי לשנות את החלטות שהתקבלו (האלגוריתם לא יחזור ויבקר בצומת שהוא כבר ביקר בו).

קוד פייתון ליישום אלגוריתם על שם דייקסטרה

אחרי שהסברנו את האלגוריתם הגיע הזמן ליישם גרסה שלו למציאת הנתיב הקצר ביותר בין שני צמתים:

import heapq

def find_shortest_path(graph: dict, start: str, end: str) ->[[], float]:
    # ... rest of Dijkstra's algorithm implementation …

היישום מסתמך על תור עדיפויות (priority queue), בו פריטים מעובדים על פי מידת הקדימות שלהם - קודם הדחוף ביותר. במקרה שלנו, אנחנו צריכים את הצומת בו טרם ביקרנו הנמצא במרחק הקצר ביותר מנקודת המוצא בכל פעם. לצורך יישום תור עדיפויות ייבאנו את הספרייה heapq של פייתון.

האלגוריתם יקבל 3 קלטים:

• graph - ייצוג של גרף באמצעות רשימת סמיכויות adjacency list
• start - מחרוזת המייצגת את צומת המוצא
• end - מחרוזת המייצגת את צומת היעד

האלגוריתם יחזיר 2 פלטים:

• path - רשימה המחזיקה את סדר הצמתים בנתיב הקצר ביותר בין start ל-end
• distance - המרחק הקצר ביותר בין start ל-end

ניצור מספר מבני נתונים שישמשו אותנו לפתרון הבעיה:

def find_shortest_path(graph: dict, start: str, end: str):
    # List all the nodes in the graph
    nodes = list(graph.keys())
    
    # Set to keep track of visited nodes
    visited = set()
    
    # Dictionary to store previous node for each node
    parents = {start: None}
    
    # Dictionary to store the shortest known distances from the start node to all other nodes
    # Start node has a path of 0 to itself while the other nodes have a value of infinity by default
    distances = {node: 0 if node == start else float("infinity") for node in nodes}

• nodes - רשימה של כל הצמתים בגרף.
• visited - סט ריק העוקב אחר הצמתים בהם ביקרנו במהלך סריקת הגרף במטרה למנוע ביקור חוזר.
• parents - מילון לעקוב אחר הצומת הקודם לכל צומת כפי שמתגלה במהלך יישום האלגוריתם. הקודם לצומת המוצא הוא None כי אין צומת הבא לפניו.
• distances - מילון המתעדכן במרחק הקצר ביותר הידוע מצומת המוצא לכל אחד מהצמתים כאשר הערכים מהם מתחילים הם 0 לצומת המוצא ואינסוף לכל היתר.

מבנה נתונים נוסף הוא רשימה שמייד הופכת לתור עדיפויות המקיים סדר של min-heap מה שיאפשר לנו לקבל את הצומת בו טרם ביקרנו הנמצא במרחק הקצר ביותר מצומת המוצא בכל שלב של ריצת האלגוריתם:

# Priority queue to keep the shortest distance from the start node at the highest priority
shortest_distance_from_start = [(distances[node], node) for node in nodes]
heapq.heapify(shortest_distance_from_start)

• הרשימה כוללת את מרחק הצומת מצומת המוצא ואת זהות הצומת

החלק העיקרי של עבודת האלגוריתם נעשה במסגרת לולאה הרצה כל עוד ישנם צמתים בהם טרם ביקרנו (משמע, תור העדיפויות טרם התרוקן):

# Main loop: continue until the priority queue is empty
while shortest_distance_from_start:
    # Run the main part of the algorithm 

בתוך הלולאה, אנחנו קודם כל מסירים את הצומת הנמצא בעדיפות הגבוהה ביותר מה שאומר שהוא הכי קרוב לצומת המוצא יחד עם המרחק שלו מצומת המוצא:

# Main loop: continue until the priority queue is empty
while shortest_distance_from_start:
    # Pop the node with the shortest distance from the priority queue
    current_node_distance, current_node =   heapq.heappop(shortest_distance_from_start)

הצומת הנמצא בעדיפות הגבוהה ביותר מאכלס את המשתנה current_node ומרחק הצומת מצומת המוצא הופך להיות ערכו של המשתנה current_node_distance.

עדיין בתוך הלולאה, נבדוק שטרם ביקרנו בצומת הנוכחי, כדי למנוע מצב שבו נבקר פעם נוספת בצומת בו כבר ביקרנו:

# Skip current node if it has been visited
if current_node in visited:
    continue

נחשב את המרחק של כל שכן מצומת המוצא. אם מרחק זה קצר יותר מהמרחק הידוע נעדכן את המרחק, את הצומת הקודם לשכן ואת תור הקדימויות:

# Explore neighbors of the current node
for neighbor, weight in graph[current_node].items():
# Skip neighbor that has been visited
    if neighbor in visited:
        continue
    # Calculate the tentative distance through the current node
    distance_from_start_to_neighbor = current_node_distance + weight
    # Update distance and parent if shorter than the known distance
    if distance_from_start_to_neighbor < distances[neighbor]:
        distances[neighbor] = distance_from_start_to_neighbor
        heapq.heappush(shortest_distance_from_start, (distance_from_start_to_neighbor, neighbor))
        previous_to_node[neighbor] = current_node

מאחר שסיימנו לסרוק את כל השכנים של ה-current_node נסמן אותו כמי שביקרנו בו כדי שלא נוכל לבקר בו שנית:

# Mark the current node as visited
visited.add(current_node)

אחרי שהלולאה תסיים לרוץ על כל הצמתים תהיה לנו רשימה של המרחקים של כל הצמתים מצומת המוצא במילון distances. אנחנו יכולים לגשת ל-distances ולשלוף מתוכו את המרחק של צומת היעד end:

# Get the shortest distance to the end node
distance_to_end = distances[end]

בנוסף, אנחנו יכולים לשחזר את הנתיב המוביל מצומת היעד end לצומת המוצא start:

# Reconstruct the shortest path from start to end
path = []
current = end
while current:
    path.append(current)
    if current in previous_to_node:
        current = previous_to_node[current]
    else:
        current = None

מכיוון שאנו מתעניינים בנתיב ההפוך המוביל מצומת המוצא לצומת היעד, נהפוך את הרשימה המתקבלת:

# Reverse the path to start from the source
path = path[::-1]

בסופו של דבר, הפונקציה מחזירה את אורך הנתיב ואת רשימת הצמתים המובילים מצומת המוצא לצומת היעד:

return path, distance_to_end

ועכשיו הכל ביחד:

import heapq
from typing import Dict, List, Tuple

def find_shortest_path(graph: dict, start: str, end: str) -> Tuple[List[str], float]:
    # List all the nodes in the graph
    nodes = list(graph.keys())
    
    # Set to keep track of visited nodes
    visited = set()
    
    # Dictionary to store previous node for each node
    previous_to_node = {start: None}
    
    # Dictionary to store the shortest known distances from the start node to all other nodes
    # Start node has a distance of 0 to itself while the other nodes have a value of infinity as default
    distances = {node: 0 if node == start else float("infinity") for node in nodes}
    
    # Priority queue to keep the shortest distance from the start node at the highest priority
    shortest_distance_from_start = [(distances[node], node) for node in nodes]
    heapq.heapify(shortest_distance_from_start)
    
    # Main loop: continue until the priority queue is empty
    while shortest_distance_from_start:
        # Pop the node with the shortest distance from the priority queue
        current_node_distance, current_node = heapq.heappop(shortest_distance_from_start)
        
        # Skip current node if it has been visited
        if current_node in visited:
            continue
        
        # Explore neighbors of the current node
        for neighbor, weight in graph[current_node].items():
            # Skip neighbor that has been visited
            if neighbor in visited:
                continue
            
            # Calculate the tentative distance through the current node
            distance_from_start_to_neighbor = current_node_distance + weight
            
            # Update distance and parent if shorter than the known distance
            if distance_from_start_to_neighbor < distances[neighbor]:
                distances[neighbor] = distance_from_start_to_neighbor
                heapq.heappush(shortest_distance_from_start, (distance_from_start_to_neighbor, neighbor))
                previous_to_node[neighbor] = current_node
                
        # Mark the current node as visited
        visited.add(current_node)
                
    # print(previous_to_node)
    # print(distances)
    
    # Get the shortest distance to the end node
    distance_to_end = distances[end]
    
    # Reconstruct the shortest path from start to end
    path = []
    current = end
    while current:
        path.append(current)
        if current in previous_to_node:
            current = previous_to_node[current]
        else:
            current = None

    # Reverse the path to start from the source
    path = path[::-1]  
    
    return path, distance_to_end

נבחן את האלגוריתם:

# Test cases


# Graph definition and testing
# Add nodes
graph = {
    "S": {}, # Start
    "A": {},
    "B": {},
    "C": {},
    "D": {},
    "F": {} # Finish
}  

# Add edges and weights
# Graph can't have a cycle
# Weights can't be negative
graph["S"]["A"] = 5
graph["S"]["B"] = 2
graph["A"]["C"] = 3
graph["A"]["D"] = 1
graph["B"]["A"] = 1
graph["B"]["C"] = 6
graph["C"]["D"] = 4
graph["C"]["F"] = 2
graph["D"]["F"] = 8
graph["F"] = {} # Finish doesn't have neighbors

path, distance = find_shortest_path(graph, "S", "F")
print(f"path from start to end = {path}")
print(f"distance from start to end = {distance}")

התוצאה:

path from start to end = ['S', 'B', 'A', 'C', 'F']
distance from start to end = 8

ננסה את הקוד על גרף מנותק שבו לא ניתן למצוא נתיב:

# Test case 2: Disconnected graph
graph = {
    "S": {}, # Start
    "B": {},
    "C": {},
    "D": {},
    "F": {} # Finish
}  

graph["S"]["B"] = 2
graph["B"]["C"] = 6
graph["D"]["F"] = 8
graph["F"] = {} # Finish doesn't have neighbors

path, distance = find_shortest_path(graph, "S", "F")
print(f"path from start to end = {path}")
print(f"distance from start to end = {distance}")

התוצאה:

path from start to end = ['F']
distance from start to end = inf

נבדוק מה קורה במקרה של משקל שלילי בגרף:

# Test case 3: Graph with negative weights
graph = {
   "S": {}, # Start
   "B": {},
   "F": {} # Finish
}


graph["S"]["B"] = 4
graph["S"]["F"] = 1
graph["B"]["F"] = -7


path, distance = find_shortest_path(graph, "S", "F")
print(f"path from start to end = {path}")
print(f"distance from start to end = {distance}")

התוצאה:

path from start to end = ['S', 'F']
distance from start to end = 1

אינה הנתיב הקצר ביותר שכן הנתיב הקצר ביותר הוא -3 והוא עובר דרך B. זו דוגמה לכך שאלגוריתם דייקסטרה עלול להפיק תוצאות שגויות כשעובדים על גרפים בעלי משקל שלילי.

מדוע אלגוריתם דייקסטרה לא עובד עבור גרפים בעלי משקלים שליליים?

כדי להבין מדוע אלגוריתם דייקסטרה לא יכול לעבוד במקרה של קשתות בעלות משקלים שליליים negative weights edges נעזר בדוגמה של הגרף הבא:

המשקלים כוללים ערך שלילי:

S -> B = 4
S -> F = 1
B -> F = -7

ניישם את אלגוריתם דייקסטרה על הגרף כאשר צומת המוצא הוא S.

נתחיל מזה שנגדיר את המרחק של צומת המוצא לעצמו כ-0, והמרחק לכל צומת אחר כ-∞:

distances['S'] = 0
distances['B'] = ∞
distances['F'] = ∞

תור העדיפויות priority queue יאכלס את הצמדים של המרחק וזהות הצומת:

shortest_distance_from_start = [(0, S), (∞, B), (∞, F)]

בפעם הראשונה בה הלולאה רצה נסיר את הפריט הראשון, זה שיש לו את המרחק הקצר ביותר מצומת המוצא, מראש הערימה:

current_node_distance, current_node = (0, S)

נשארנו עם תור העדיפויות:

shortest_distance_from_start = [(∞, B), (∞, F)]

נחשב את המרחקים של שכניו של S מצומת המוצא:

distances[B] = 0 + 4 = 4
distances[F] = 0 + 1 = 1

כתוצאה מכך יעודכן תור העדיפויות:

shortest_distance_from_start = [(1, F), (4, B)]

נעביר את S לסט הצמתים בהם ביקרנו כדי שלא נבקר בו יותר.

visited = (S)

בפעם השנייה בה הלולאה רצה נסיר את הצמד:

current_node_distance, current_node = (1, F)

וכתוצאה מכך נשאר עם תור עדיפויות המכיל פריט בודד:

shortest_distance_from_start = [(4, B)]

הצומת F אינו מקושר לאף צומת. נוסיף אותו לסט הצמתים בהם ביקרנו כדי שלא נבקר בו יותר:

visited = (S, F)

עכשיו נסיר את הצמד האחרון מתור העדיפויות:

current_node_distance, current_node = (4, B)

ל-B יש קשת במשקל -7 ל-F אבל כיוון שב-F כבר ביקרנו אנחנו לא יכולים לעדכן את המרחק ל-F.

בזה סיימנו לבקר בכל הצמתים של הגרף מה שיוביל למסקנה שהמרחק הקצר ביותר של F מ-S הוא 1, אבל מהסתכלות בגרף אפשר לראות שאם מגיעים ל-F דרך B הנתיב הוא קצר יותר ממה שהסיק האלגוריתם:

S -> B -> F = 4 + (-7) = -3

ומזה אנחנו יכולים ללמוד על הבעיה שיש לאלגוריתם דייקסטרה עם מציאת הנתיב הקצר ביותר בגרפים בעלי משקל שלילי.

ממה נובעת הבעיה? בגלל שהאלגוריתם לא מעדכן את המרחקים לצמתים בהם ביקר מה שאומר שגם אם ישנו נתיב קצר יותר לצומת בו ביקר הוא לא יוכל למצוא אותו.

המסקנה: אלגוריתם דייקסטרה לא יכול לשמש למציאת המרחקים הקצרים ביותר בגרפים שיש בהם משקלים שליליים.

סיבוכיות זמן ומקום של אלגוריתם דייקסטרה

סיבוכיות הזמן במקרה הגרוע היא O(V + E) כאשר V הוא מספר הצמתים המקסימלי בו נבקר (אנחנו רשאים לבקר בכל צומת פעם אחת בלבד) ו-E הוא מספר הקשתות, כאשר תור העדיפויות תורם O(logV) מה שמביא לסיבוכיות זמן: O((V + E) log V).

סיבוכיות המקום במקרה הגרוע היא O(V) בגלל שערימת הקדימויות תחזיק לכל היותר V פריטים, כמו הסט visited והמילון previous_to_node.

היכן משתמשים בדייקסטרה?

אלגוריתם דייקסטרה מוצא את הנתיב הקצר ביותר מקודקוד מקור יחיד לכל הקודקודים האחרים בגרף מכוון וממושקל. הוא בעל יישומים רבים בתחומים שונים בשל יכולתו למצוא נתיבים קצרים. להלן כמה שימושים נפוצים באלגוריתם דייקסטרה:

1. מערכות ניתוב וניווט: אלגוריתם דייקסטרה נמצא בשימוש נרחב ביישומי ניתוב וניווטי למציאת הנתיב הקצר ביותר בין שני מיקומים. הוא מסייע בחישוב מסלולים אופטימליים עבור מערכות ניווט GPS ותוכנות ניווט דוגמת Google maps.
2. ניתוב רשתות: אלגוריתם דייקסטרה משמש ברשתות מחשבים כדי למצוא את הנתיב הקצר ביותר עבור חבילות נתונים שצריכות לעבור בין מחשבים.
3. רשתות תקשורת: אלגוריתם דייקסטרה מסייע לאופטימיזציה של מסלולי שידור נתונים ברשתות תקשורת, כולל רשתות טלפון ואינטרנט. הוא משמש כדי למזער עיכובים ולהפחית את עלות שידור הנתונים.
4. אופטימיזציה של שרשרות אספקה: בלוגיסטיקה וניהול שרשרת אספקה, אלגוריתם דייקסטרה יכול לסייע למצוא את הנתיב הקצר ביותר בו ניתן להשתמש על מנת ליעל ולקצר את מסלולי המשלוח.

אלה הם רק כמה דוגמאות ליישומים הרבים של אלגוריתם דייקסטרה. יעילותו ויכולתו לפתור את הנתיבים הקצרים ביותר הפכו אותו לכלי חשוב בתחומים שונים שבהם אופטימיזציה של מסלולים היא קריטית.

יתרונות וחסרונות של אלגוריתם דייקסטרה

אלגוריתם דייקסטרה מוצא את הנתיב הקצר ביותר בין צומת היעד לכל צומת אחר בפשטות יחסית ועל כן הוא משמש במערכות רבות אבל הוא לא יודע לעבוד עם גרפים שיש בהם קשתות בעלות משקל שלילי, כפי שכבר הסברנו.

חסרון עיקרי נוסף נובע מהגישה החמדנית וקצרת הרואי של אלגוריתם דייקסטרה.

אלגוריתם דייקסטרה נחשב לאלגוריתם חמדן וזה בגלל שבכל שלב מבקרים בצומת שיש לו את המרחק הקצר ביותר מצומת המוצא כי ההנחה היא שיש לקחת את האפשרות הטובה ביותר הנראית לעין בכל שלב, בלי לקחת בחשבון פתרונות אחרים שהם אולי טובים יותר. רק ששימוש באלגוריתם חמדן לא תמיד ייתן את התוצאה הטובה ביותר. נסתכל על הגרף הבא:

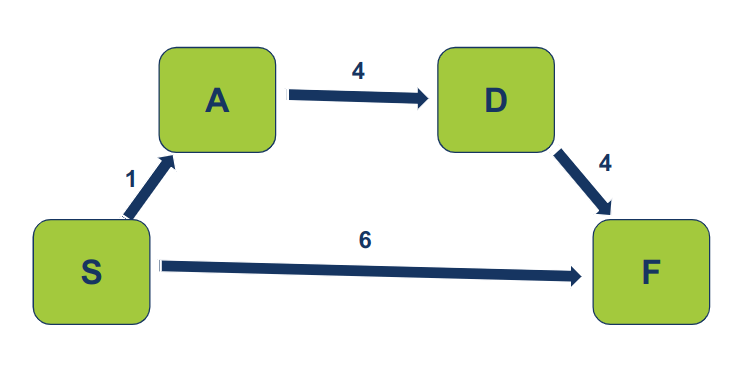
בהנחה שאנחנו מעוניינים להגיע מ-S ל-F בדרך הקצרה ביותר. אם נאמץ את הגישה החמדנית הבוחרת את הנתיב הקצר ביותר בכל שלב נבחר בנתיב מ-S ל-A שיוביל לנתיב ארוך יותר ל-F . גישה חלופית, שאינה חמדנית, הייתה מובילה אותנו לבחור בנתיב הישיר מ-S ל-F שהוא קצר יותר.

כדי להתמודד עם חלק מהבעיות של אלגוריתם דייקסטרה פותח אלגוריתם Bellman-Ford שיודע לעבוד עם גרפים שיש בהם קשתות בעלות משקלים שליליים. חלופה נוספת, היא אלגוריתם A* המשתמש בהיוריסטיקה לבחירת הנתיבים העדיפים. לדוגמה, אם אני מעוניין ליסוע מתל אביב דרומה אין לי עניין שהאלגוריתם יחשב את הנתיבים המובילים לצפון אז בעוד דייקסטרה יחשב את כל הנתיבים, לצפון ולדרום, A* יתמקד בנתיבים הרלבנטיים.

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

פתרון בעיות אופטימיזיציה באמצעות אלגוריתם חמדן

יישום רשימת סמיכויות adjacency list - חלק ב בסדרה על גרפים

הבנת אלגוריתם חיפוש לרוחב - BFS - סריקה של גרפים ומציאת הנתיב הקצר ביותר

אלגוריתם חיפוש לעומק DFS - מהבנה ליישום

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים