חידה תכנותית: מיכל עם הכי הרבה מים

תיאור הבעיה:

ניתן לך מערך של גבהים `heights` באורך n. כל פריט מערך מציין גובה. עליך למצוא שני גבהים (=פריטי מערך) שביחד עם ציר ה-x יוצרים מיכל, כך שהמיכל יכיל את כמות המים המקסימלית.

לדוגמה, אם נתון מערך גבהים:

[2, 2]

אז הגובה המקסימלי הוא בהכרח:

2

למה? האיור הבא מסביר את אופן החישוב:

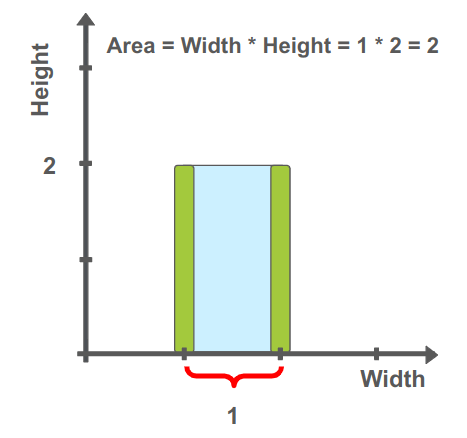
במילים פשוטות, בהינתן מערך של גבהים, כאשר המרחק בין כל שני גבהים הוא 1, יש למצוא שילוב של גובה ומרחק שייתן את השטח המקסימלי.

דוגמה נוספת. נתון מערך גבהים:

[2, 1, 3]

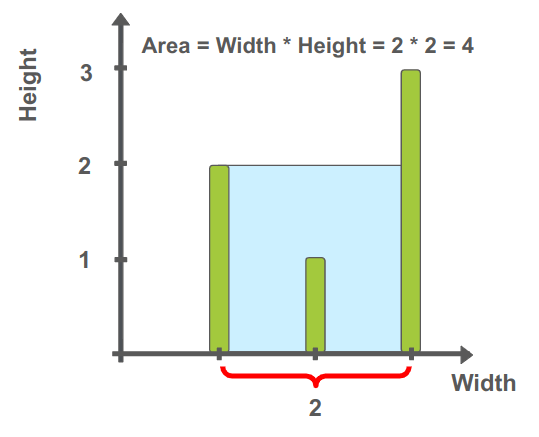
בתוך המערך ישנם 3 שטחים אפשריים:

• כדי לחשב את השטח התחום בין הגבהים 2 ל-1 יש לקחת בחשבון את המרחק בין הגבהים שהוא 1, ואת הגובה הנמוך מבין השניים שהוא 1, ואז לפי נוסחת השטח שהיא גובה * אורך נחשב שטח של: 1 * 1 = 1

• לפי אותו היגיון, השטח התחום בין הגבהים 1 ו-3 גם הוא 1.

• כאשר הגבהים התוחמים הם 2 ו-3, הגובה המינימלי מבין הגבהים התוחמים הוא 2 והמרחק בין הגבהים התוחמים הוא 2, ובהתאם השטח הוא: 2 * 2 = 4

מבין שלוש השטחים שטח של 4 הוא הגבוה ביותר ולכן הצפי הוא שעבור קלט של מערך 2,1,3 הפונקציה תנפק את הפתרון 4.

האיור הבא מסביר את הפתרון:

פתרון יעיל המבוסס על טכניקת שני המצביעים

בהינתן מערך של גבהים, כאשר המרחק בין כל שני גבהים הוא 1, יש למצוא שילוב של גובה ומרחק שייתן את השטח המקסימלי כאשר הגובה מוגבל על ידי הנמוך מבין שני הגבהים התוחמים.

נפתור את הבעיה באמצעות שני מצביעים שירוצו משני צידי המערך תוך זכירת השטח המקסימלי שחושב בתהליך.

המטרה של הפונקציה הזו היא לחשב את השטח המקסימלי שניתן ללכוד בין שני גבהים. דרך יעילה ביותר לפתור את הבעיה היא באמצעות טכניקת שני המצביעים.

הפונקציה `container_with_most_water()` מקבלת רשימה של גבהים (`heights`) כקלט. המטרה של הפונקציה היא לחשב את השטח המקסימלי שניתן ללכוד בין שני קווים בגבהים הנתונים. לשם כך, הפונקציה משתמשת בטכניקת שני המצביעים, כאשר `left_cursor` ו-`right_cursor` מאותחלים לתחילת ולסוף הרשימה. מצביעים אלו מייצגים את הרוחב המרבי האפשרי של המיכל.

def container_with_most_water(heights):
    # Goal: compute the maximum area 
    # that can't be less than zero
    max_area = 0
    
    # For this, we use the two pointers technique
    # Initialize two cursors at the ends, representing the maximum width
    left_cursor = 0
    right_cursor = len(heights) - 1

הקוד נכנס ללולאה שממשיכה לרוץ כל עוד שני המצביעים לא נפגשו באמצע הרשימה. לולאה זו חיונית למציאת השטח המקסימלי.

# Keep iterating as long as the 2 cursors haven't met
while left_cursor < right_cursor:
    # Get the heights at the left and right cursor positions
    left_height = heights[left_cursor]
    right_height = heights[right_cursor]

• בתוך הלולאה, הקוד מקבל את הגבהים של הקווים בעמדות הנוכחיות של `left_cursor` ו-`right_cursor`.

`container_height` מייצג את גובה המיכל, והוא נקבע על ידי הקצר מבין שני הקווים. גובה המיכל תמיד מוגבל על ידי הקו הקצר יותר.

# The container's height is limited by the shorter side
 container_height = min(left_height, right_height)

`local_area` מחושב על ידי הכפלת `container_height` ורוחב המיכל, שהוא ההפרש בין העמדות של `left_cursor` ו-`right_cursor`.

אם `local_area` גדול מ-`max_area` שנמצא עד כה, הוא מעדכן את `max_area` ל-`local_area` החדש. שלב זה מבטיח שהפונקציה תמיד עוקבת אחר השטח המקסימלי.

# Calculate the local area by multiplying height and width
local_area = container_height * (right_cursor - left_cursor)
        
# Update the maximum area if a larger area is found
if local_area > max_area:
    max_area = local_area

לבסוף, הוא מקדם את המצביע עם הגובה הנמוך יותר מכיוון שייתכן שיש קו גבוה יותר בהמשך. שלב זה מבטיח שהאלגוריתם חוקר שילובים שונים של גבהים ורוחבים.

# Advance the cursor with the lower height as it may find a higher side
if left_height < right_height:
    left_cursor = left_cursor + 1
else:
    right_cursor = right_cursor - 1

לאחר שהלולאה מסיימת לרוץ, הפונקציה מחזירה את `max_area`, שמייצג את כמות המים המקסימלית שניתן ללכוד בין הקווים.

עכשיו הכל ביחד:

def container_with_most_water(heights):
    # Goal: compute the maximum area 
    # that can't be less than zero
    max_area = 0
    
    # For this, we use the two pointers technique
    # Initialize two cursors at the ends, representing the maximum width
    left_cursor = 0
    right_cursor = len(heights) - 1
    
    # Keep iterating as long as the 2 cursors haven't met
    while left_cursor < right_cursor:
        # Get the heights at the left and right cursor positions
        left_height = heights[left_cursor]
        right_height = heights[right_cursor]
        
        # The container's height is limited by the shorter side
        container_height = min(left_height, right_height)
        
        # Calculate the local area by multiplying height and width
        local_area = container_height * (right_cursor - left_cursor)
        
        # Update the maximum area if a larger area is found
        max_area = max(max_area, local_area)
        
        # Advance the cursor with the lower height as it may find a higher side
        if left_height < right_height:
            left_cursor = left_cursor + 1
        else:
            right_cursor = right_cursor - 1
        
    return max_area

נבחן את הפתרון:

# Test cases
heights = [2,2]
print(container_with_most_water(heights)) # 2

heights = [2,1]
print(container_with_most_water(heights)) # 1

heights = [2,1,2]
print(container_with_most_water(heights)) # 4

heights = [1,2,1,2]
print(container_with_most_water(heights)) # 4

heights = [2,1,2,1]
print(container_with_most_water(heights)) # 4

heights = [2,1,2,1,1,1]
print(container_with_most_water(heights)) # 5

heights = [1,3,1,3,1,1]
print(container_with_most_water(heights)) # 6

heights = [1,8,6,2,5,8,3]
print(container_with_most_water(heights)) # 32

heights = [1,8,6,2,5,4,8,3,7]
print(container_with_most_water(heights)) # 49

heights = [1,5,4,3]
print(container_with_most_water(heights)) # 6

heights = []
print(container_with_most_water(heights)) # 0

ניתוח ביצועים

• סיבוכיות זמן: הפונקציה מאופיינת בסיבוכיות זמן לינארית O(N), כאשר N הוא אורך המערך `heights` מפני שהיא עוברת על המערך פעם אחת עד ששני המצביעים נפגשים באמצע.

• סיבוכיות מקום: לפונקציה סיבוכיות מקום O(1), שהיא קבועה מכיוון שהיא משתמשת במשתנים התופסים מקום קבוע בזכרון ללא תלות במידות הקלט.

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

שימוש בטכניקת שני המצביעים לפתרון בעיות תכנותיות

חידה תכנותית: twoSum

טכניקת חלון ההזזה sliding window לפתרון בעיות ברצפים

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים