שימוש בטכניקות שני המצביעים לפתרון בעיות תכנותיות

השימוש בטכניקות המבוססות על שני מצביעים Two pointers technique הוא מאוד מקובל כשרוצים לפתור בעיות של רצפים כמו מחרוזות, מערכים ורשימות מקושרות linked list. כאשר משתמשים ב-שני מצביעים כדי לעבור על רצף בדרך המאפשרת בחינת פריטים או תווים או תוך שמירה על יחס בין המצביעים.

כשמשתמשים בשני מצביעים לפתרון בעיות תכנותיות בדרך כלל עושים אחד משניים:

1. מצביע אחד מתחיל להתקדם מהסוף להתחלה והשני מההתחלה לסוף עד שהם נפגשים.
2. מצביע אחד נע בקצב איטי, בעוד שהמצביע השני נע בקצב כפול.

סיבוכיות הזמן לפתרון בעיות באמצעות טכניקת שני המצביעים תלויה במקרה. במקרה הטוב, הטכניקה יכולה להגיע לסיבוכיות זמן ליניארית O (n). זה המצב כשעובדים עם רצפים ממוינים. במקרים מסוימים, כאשר הבעיה דורשת מיון הרצף תחילה, סיבוכיות הזמן יכולה להיות O (n log n) עקב פעולת המיון.

מדריך זה יציג דוגמאות שימוש שונות בטכניקה של שני מצביעים. הבעיה הראשונה "Sorted two sum" היא לכאורה קלה לפתרון אבל היא גם מדגימה למה לא תמיד כדאי לרוץ לפתרון הראשון שעולה על הדעת, בפרט אם הפתרון הוא brute force, ומדוע שימוש בטכניקה של שני מצביעים עשוי להיות פתרון מוצלח הרבה יותר.

אתגר: Sorted two sum

תיאור:

נתון רצף ממוין של מספרים שלמים nums ומספר שלם target, עליך להחזיר את האינדקסים של שני המספרים שסכומם שווה ל-target.

הנחות:

• פריטי המערך מסודרים בסדר עולה.
• לכל רצף יכול להיות לכל היותר פתרון אחד או שלא יהיה פיתרון.
• אינך יכול להשתמש באותו פריט פעמיים.

אתה צריך לכתוב פונקציה:

def two_sum_sorted(nums):
    # Your code

הלוקחת רצף ממוין של מספרים שלמים nums ומספר שלם target. הפונקציה צריכה להחזיר רשימה של שני אינדקסים המייצגים את המיקומים של שני המספרים ברצף שסכומם משתווה לסכום המטרה.

דוגמה:

nums = [7, 8, 13, 15]
target = 22
res = two_sum(nums, target)
# Output: [0, 3] # nums[0] + nums[3] = 22

הפתרון הראשון שקופץ לראש עשוי להיות פתרון brute force הכולל הרצת לולאה בתוך לולאה. לולאה חיצונית הרצה על כל פריטי המערך מהפריט הראשון ועד האחד לפני אחרון, ולולאה הפנימית הרצה על כל הפריטים שבין האינדקס + 1 שבו נמצאת הלולאה החיצונית ועד לסוף המערך. פתרון זה מבטיח בדיקה של כל הזוגות האפשריים.

כך נראה קוד ה-brute force:

def two_sum_brute_force(nums, target):
    if len(nums) < 2:
        return []
        
    for idx in range(0, len(nums) - 1):
        # Start from idx + 1 to avoid using the same element twice
        for inner_idx in range(idx + 1, len(nums)):  
            if nums[idx] + nums[inner_idx] == target:
                return [idx, inner_idx]
        
    return []

# Example 1
nums = [7, 8, 15, 18]
target = 22
res = two_sum_brute_force(nums, target)
print(res)

# Example 2
nums = [-3, -2, -1, 2, 3, 9]
target = 6
res = two_sum_brute_force(nums, target)
print(res)

סיבוכיות הזמן של הפתרון brute force היא O(n^2) הנובעת ממכפלת זמן הביצוע של כל אחת מהלולאות שהינו n. זו סיבוכיות זמן לא יעילה שטכניקת שני המצביעים יכולה לעזור לקצר אותה באופן משמעותי.

לצורך פתרון הבעיה נפעיל את הגרסה של טכניקת שני המצביעים המפעילה שני מצביעים אחד הרץ מימין לשמאל ושני הרץ משמאל לימין עד שהם נפגשים באמצע:

def two_sum(nums, target):
    if len(nums) < 2:
        return []
        
    left_cur = 0
    right_cur = len(nums) - 1
    while left_cur != right_cur:
        sum = nums[left_cur] + nums[right_cur]
        if sum == target:
            return [left_cur, right_cur]
        elif sum > target:
            right_cur -= 1
        else:
            left_cur += 1
        
    return []

# Example 1
nums = [7, 8, 13, 15]
target = 22
res = two_sum(nums, target)
print(res)

# Example 2
nums = [-4, -3, -1, 2, 9, 11, 12]
target = 6
res = two_sum(nums, target)
print(res)

# Example 3
nums = [-4, -3, -1, 2, 8, 11, 12]
target = 6
res = two_sum(nums, target)
print(res)

נסביר:

הפונקציה יוצרת שני מצביעים, left_cur בתחילת הרשימה ו-right_cur בסוף הרשימה.

הפונקציה נכנסת ללולאה while שתמשיך עד לפגישת שני המצביעים באמצע המערך באופן שהמצביעים לא יעלו אחד על השני.

בתוך הלולאה, נעשה חישוב סכום החיבור בין: sum = nums[left_cur] + nums[right_cur].

את הסכום sumמשווים עם ערך המטרה target ופועלים בהתאם:

• אם הסכום שווה למטרה, אז הפונקציה תחזיר את האינדקסים של המצביעים הנוכחיים.
• אם הסכום קטן מהיעד, מקדמים את המצביע left_cur (המצביע על הערכים הנמוכים של המערך) צעד אחד ימינה לעבר ערך גבוה יותר.
• אם הסכום גדול מהיעד, מסיגים את המצביע right_cur (המצביע על הערכים הגבוהים של המערך) צעד אחד שמאלה לעבר ערך נמוך יותר.

אם לא נמצא זוג השווה למטרה, מוחזר מערך ריק.

פתרון זה משתמש במצביעים הנעים בכיוונים מנוגדים ומנצל את העובדה שהרשימה nums היא ממויינת. הוא משיג סיבוכיות זמן ליניארית של O(n) מכיוון ששני המצביעים יחדיו ינועו לכל היותר n פעמים (כאשר n הוא אורך הרשימה nums) עד למציאת פתרון. סיבוכיות זמן לינארית היא טובה משמעותית יותר מ-O(n^2) אליו הגענו באמצעות פתרון brute force.

אתגר: המחרוזת הארוכה ביותר ללא תווים חוזרים

נתונה מחרוזת s, מצא את המחרוזת הארוכה ביותר ללא תווים חוזרים.

עליך לכתוב פונקציה:

def longest_substring(s: str) -> str

המקבלת מחרוזת s ומחזירה את המחרוזת הארוכה ביותר ללא תווים חוזרים.

דוגמה:

# Test cases 

s0 = "ababac" 
print(longest_substring(s0)) 
# Output: The longest substring without repeating characters is "bac" 

s1 = "ffabcmmfabab" 
print(longest_substring(s1)) 
# Output: The longest substring without repeating characters is "fabcm"

s2 = "abcaabcb" 
print(longest_substring(s2)) 
# Output: The longest substring without repeating characters is "abc" 

s3 = "aaaaa" 
print(longest_substring(s3)) 
# Output: The longest substring without repeating characters is "a" 

s4 = "addcfg" 
print(longest_substring(s4)) 
# Output: The longest substring without repeating characters is "dcfg"

s5 = "" 
print(longest_substring(s5)) 
# Output: The longest substring without repeating characters is ""

הערות:

• תת מחרוזת היא רצף רציף contiguous של תווים בתוך המחרוזת.
• אתה יכול להניח שהמחרוזת מכילה רק אותיות קטנות באנגלית.

כדי למצוא את תת-המחרוזת הארוכה ביותר ללא תווים חוזרים נשתמש בשני מצביעים (pointers), שמאלי וימני, אשר ייצגו את תת-המחרוזת הנוכחית. נזיז את המצביע הימני כדי להרחיב את החלון עד שנפגוש תו חוזר. כאשר נמצא תו חוזר, נזיז את המצביע השמאלי כדי לצמצם את החלון. במסגרת התהליך נעקוב אחר תת-המחרוזת הארוכה ביותר שמצאנו עד כה אותה תחזיר הפונקציה בסופו של דבר.

def longest_substring(s):
    max_substring = ""

    left = 0
    right = 0

    seen = set()

    while right < len(s):
        if s[right] not in seen:
            seen.add(s[right])
            right += 1
            if right - left > len(max_substring):
                max_substring = s[left:right]
        else:
            seen.remove(s[left])
            left += 1

    return max_substring

תזכורת לגבי רשימות מקושרות Linked Lists

הסברתי על מבנה הנתונים רשימה מקושרת Linked List במדריך קודם. מי שלא מכיר את הנושא כדאי שיקרא את המדריך. מי שכבר יודע מוזמן לרענן את זכרונו עם הפסקאות הבאות.

רשימה מקושרת (Linked list) היא מבנה נתונים פשוט המורכב מאלמנטים שנקראים "צמתים" (nodes). כל צומת מכיל שני חלקים: מידע (data) ומצביע (רפרנס) לצומת הבא ברשימה. היתרון העיקרי של רשימה מקושרת קשור באופייה הדינמי. בניגוד למערכים, אורכם של רשימות מקושרות משתנה מבלי לדרוש הקצאת מקום מראש בזיכרון. הגמישות הזו מאפשרת לנו להתאים את הרשימה למספר הנתונים המשתנה בתוכנית, מה שהופך אותה לפתרון מוצלח עבור מקרים בהם כמות הנתונים עשויה להשתנות באופן תדיר.

רשימה מקושרת בנויה מאיברים, Nodes. לכל איבר 2 תכונות, מידע data ומצביע reference על האיבר הבא ברשימה.

להלן קלאס פייתון ליישום Node:

class Node: 
    def __init__(self, data): 
        self.data = data 
        # Pointer to the next node in the list
        self.next = None 

האיבר הראשון ברשימה נקרא head, ואין מצביע next אשר מצביע עליו. אם הרשימה ריקה אז ה-head יצביע על שום מקום בזיכרון None. הקלאס LinkedList מיישם רשימה מקושרת:

class LinkedList: 
    def __init__(self): 
    self.head = None

כל איבר ברשימה מקושרת מצביע על האיבר הבא בתור (המצביע next). האיבר בזנב הרשימה מצביע על null.

כדי להוסיף איבר (צומת) לרשימה אנחנו צריכים שהוא יהיה Node. במידה והרשימה ריקה נוסיף את ה-node בתור ראש הרשימה head. במידה ולא, נכוון את המצביע next של האיבר האחרון ברשימה על ה-node החדש.

המתודה append() תוסיף צומת לסוף הרשימה:

class LinkedList:
    def __init__(self):
        # Pointer to the first node in the list
        self.head = None  

    def append(self, data):
        new_node = Node(data)
        if not self.head:
            self.head = new_node
        else:
            current = self.head
            while current.next:
                current = current.next
             current.next = new_node
        return new_node

• המתודה append() יוצרת node עם המידע שהיא מקבלת בפרמטר data. את ה-node היא מוסיפה לזנב הרשימה. לבסוף, המתודה מחזירה את ה-node החדש.

כדי להציג את הרשימה נוסיף את המתודה display() לקלאס. המתודה תעבור אחד אחד על איברי הרשימה ותדפיס כל אחד מהם:

def display(self):
        current = self.head
        while current:
            print(current.data, end=" -> ")
            current = current.next
        print("None")

ננסה את הקוד:

# Create a linked list and add elements
linked_list = LinkedList()
linked_list.append(1)
linked_list.append(2)
linked_list.append(3)

# Display the linked list
linked_list.display()

התוצאה:

1 -> 2 -> 3 -> None

אתגר: זיהוי הפניות מעגליות ברשימה מקושרת linked list

נתונה רשימה מקושרת ואתה צריך לבדוק האם היא מכילה הפניות מעגליות cycle. לצורך ביצוע המשימה אתה יכול להעזר בפונקציה שזה המבנה שלה:

def has_cycle(head: Node) -> bool:
    pass

• קלט: הפונקציה has_cycle מקבלת head של רשימה מקושרת כ- input.
• פלט: הפונקציה מחזירה ערך בוליאני True או False על סמך קיום הפנייה מעגלית ברשימה המקושרת.

דוגמאות:

אם נעביר לפונקציה קלט המכיל הפנייה מעגלית:

1 -> 2 -> 3 -> 1

• נצפה מהפונקציה להחזיר True כי הרשימה מתחילה עם node 1 ובהמשך הרשימה node 3 מצביע חזרה על node 1

לעומת זאת הקלט:

1 -> 2 -> 3

• יחזיר False כי אין הרשימה כוללת הפנייה מעגלית.

רמז:

אנחנו צריכים להגדיר את המצביע next של הצומת האחרון כדי שיצביע על האיבר הראשון ברשימה. כך נעשה זאת:

ll = LinkedList() 
n1 = ll.append(1) 
n2 = ll.append(2) 
n3 = ll.append(3) 
n3.next = n1

אם נעשה את הטעות וננסה להריץ את המתודה display() אז היא תרוץ בלולאה אינסופית כיוון שהרשימה מכילה הפנייה מעגלית.

לפתרון הבעיה נשתמש באלגוריתם הצב והארנב של Floyd, הידוע גם בשם "אלגוריתם גילוי המעגל של Floyd" או "גילוי מעגל באמצעות שני מצביעים". זו טכניקה המשתמשת בשני מצביעים לגילוי הפניות מעגליות ברשימה מקושרת. זהו אלגוריתם פשוט ויעיל שאינו דורש זיכרון נוסף.

כך עובד האלגוריתם:

1. הגדרה: התחל עם שני מצביעים, המכונים לעתים קרובות "צב" ו"ארנב". שני המצביעים מתחילים בראש הרשימה המקושרת.
2. סיור: בכל שלב, העבר את הצב צעד אחד קדימה והעבר את הארנב שני צעדים קדימה. זה מדמה מירוץ בין שני המצביעים.
3. גילוי מעגל: אם אין מעגל ברשימה המקושרת, הארנב יגיע בסופו של דבר לסוף הרשימה. לעומת זאת, אם קיים מעגל, הארנב והצב יפגשו דבר המלמד על נוכחותו של מעגל ברשימה המקושרת.

הסיבה שאלגוריתם זה עובד מבוססת על המהירויות היחסיות של הצב והארנב. אם יש מעגל, הארנב ידביק בסופו של דבר את הצב כיוון שהוא מקיף את המעגל מהר יותר. זה דומה לשני רצים על מסלול מעגלי כאשר אחד איטי יותר מהשני. בסופו של דבר, הרץ המהיר יותר (הארנב) יגיע לרץ האיטי יותר (הצב) כאשר שניהם רצים סביב המסלול.

קוד הפייתון הבא מיישם את אלגוריתם "הצב והארנב" לצורך זיהוי הפניות מעגליות ברשימה מקושרת:

def has_cycle(head: Node):
    # 1. Both pointers begin at the head of the linked list
    slow = head
    fast = head
    
    # 2. Traversal limited by the `fast` existence or pointing the a next node
    while fast and fast.next:
        # In each step, move the `slow` one step ahead and the `fast` two steps ahead
        slow = slow.next
        fast = fast.next.next
        # 3. If the `slow` and `fast` meet, it indicates the presence of a cycle in the linked list. 
        if slow == fast:
            return True
        
    # Default value when no cycle detected
    return False


# Test cases


# Test case 1: Cyclic linked list
ll1 = LinkedList()
n1 = ll1.append(1)
ll1.append(2)
n3 = ll1.append(3)
n3.next = n1


print(has_cycle(ll1.head))  # True


# Test case 2: Cyclic linked list
ll2 = LinkedList()
n1 = ll2.append(1)
n1.next = n1


print(has_cycle(ll2.head))  # True


# Test case 3: Non-cyclic linked list
ll3 = LinkedList()
ll3.append(1)
ll3.append(2)
ll3.append(3)
ll3.append(4)


print(has_cycle(ll3.head))  # False


# Test case 4: Non-cyclic linked list
ll4 = LinkedList()
ll4.append(1)


print(has_cycle(ll4.head))  # False


# Test case 5: Empty list
ll5 = LinkedList()


print(has_cycle(ll5.head))  # False

אלגוריתם הצב והארנב של Floyd הוא בעל סיבוכיות זמן של O(n), כאשר n הוא מספר הצמתים ברשימה המקושרת. זו גישת חסכונית בזיכרון ועל כן מומלץ להשתמש בו לגילוי מעגלים.

אתגר: היפוך רשימה מקושרת Linked List

נתונה רשימה מקושרת. אתה צריך להעביר את ראשה head לפונקציה שתחזיר רשימה מקושרת בה סדר הצמתים הפוך. כך צריכה להיראות הפונקציה:

def reverse_linked_list(head: Node) -> Node:
    pass

אם נזין לפונקציה את הרשימה המקושרת:

1 -> 2 -> 3 -> 4 -> None

הפונקציה תחזיר:

4 -> 3 -> 2 -> 1 -> None

אם נזין לפונקציה רשימה הכוללת איבר אחד:

1 -> None

הפונקציה תחזיר:

1 -> None

פתרון

הפתרון משתמש בשני מצביעים:

1. prev: מצביע העוקב אחר הצומת הקודם ברשימה כיוון שאין לנו מצביע על האיבר הקודם ברשימה מקושרת אנחנו צריכים משתנה שיאפשר לנו לדעת מיהו האיבר הקודם.

2. current: מצביע על הצומת הנוכחי ברשימה המקושרת.

שני המצביעים עובדים יחד כדי להפוך את הרשימה המקושרת במקום. כאשר מצביע prev מורה על האיבר הבא ברשימה ההפוכה, בעוד שמצביע curr מתקדם בתוך הרשימה המקורית. השילוב של שניהם בקוד גורם לכל איבר ברשימה ההפוכה להצביע על האיבר הקודם במקום על הבא.

אנחנו יכולים ליצור רשימה חדשה אבל זה פתרון פחות יעיל. הפתרון שלנו מבוסס על היפוך מצביעי next של כל איבר בתוך רשימה קיימת. משך הזמן הדרוש לביצוע המשימה הוא יעיל O(n) כיוון שצריך לעבור על כל איבר ברשימה שאורכה n בדיוק פעם אחת והמקום בזכרון הנדרש לפעולה הוא קבוע O(1) כיוון שגישת הפתרון מבוססת הלולאה אותה נציג מיד אינה דורשת תוספת זיכרון לצורך הפתרון כיוון שכל השינויים נעשים במקום, על ידי מניפולציה של מצביעים, ללא צורך במבני נתונים נוספים.

הקוד להלן פותר את הבעיה של היפוך הרשימה המקושרת:

def reverse_linked_list(head: Node) -> Node:
    # Initialize pointers:
    # `prev` - Keeps track of the previous node
    # `curr` - Keeps track of the current node
    prev = None
    curr = head

    # Keep iterating while the `curr` pointer hasn't reached the tail of the original list
    while curr:
        # Cache the pointer to the next node
        next = curr.next
        # Reverse the `next` pointer of the current node to point to the previous node
        curr.next = prev
        # Advance `prev` pointer to the current position
        prev = curr
        # Advance `curr` pointer to the next node in the original list
        curr = next

    # Return the head of the reversed list
    return prev


# Test cases

# Test case 1: Reverse a multi-node linked list
ll1 = LinkedList()
ll1.append(1)
ll1.append(2)
ll1.append(3)
ll1.append(4)

ll1.head = reverse_linked_list(ll1.head)
ll1.display()
# Output: 4 -> 3 -> 2 -> 1 -> None

# Test case 2: Reverse a single-node linked list
ll2 = LinkedList()
ll2.append(1)

ll2.head = reverse_linked_list(ll2.head)
ll2.display()
# Output: 1 -> None

נסביר:

המטרה היא לסובב את כיוונו של כל איבר ברשימה כך שהמצביע next של כל איבר יצביע על האיבר הקודם במקום על הבא בתור.

פתרון האתגר משתמש בשני מצביעים (Two pointers):

• curr - מצביע על האיבר הנוכחי
• prev - מצביע על האיבר הקודם

1. נאתחל את שני המצביעים:

   curr = head
   prev = None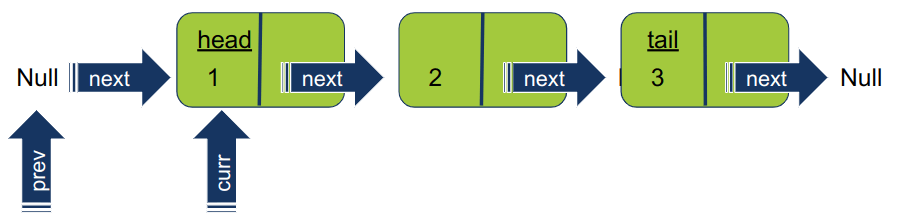

   

   • המצביע curr מצביע על ראש הרשימה ממנו מתחילים לסרוק את הרשימה.

   • המצביע prev מאותחל כ- None כי אין איבר המקדים את ראש הרשימה. המעקב אחר מיקומו של האיבר הקודם הוא חשוב כדי שנדע להיכן להפנות את המצביע next לאחר ההיפוך.

2. במסגרת ההיפוך, המצביע curr עובר להצביע על האיבר הקודם עליו מצביע prev. כך יוצא שהמצביע עובר להצביע על Null והופך את האיבר הראשון ברשימה לזנב של רשימה.

   

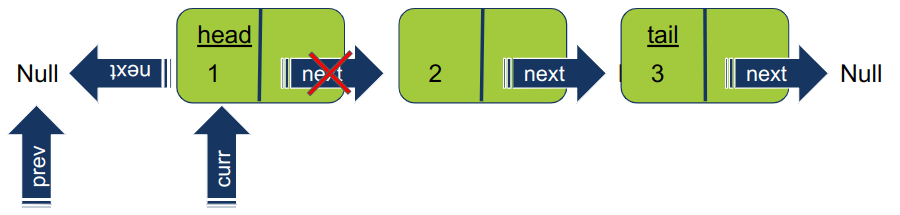
3. מזיזים את המצביעים prev ו- curr כל אחד בנפרד איבר אחד קדימה ברשימה המקורית. עכשיו prev מצביע על איבר 1 ו- curr על 2.

   

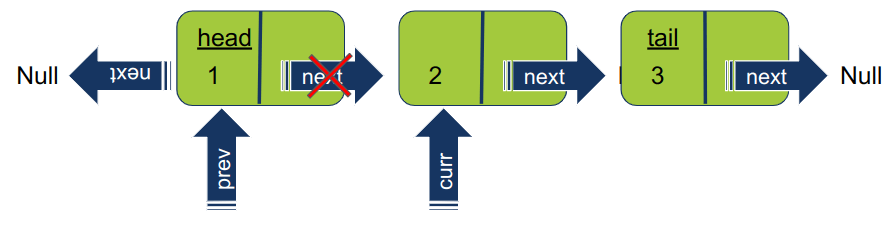
   עדיין באותו שלב. מסובבים את המצביע של האיבר עליו מצביע curr כדי שיצביע על האיבר הקודם prev. במקום בו אנו נמצאים בתהליך, האיבר 2 יעבור להצביע על 1.

   

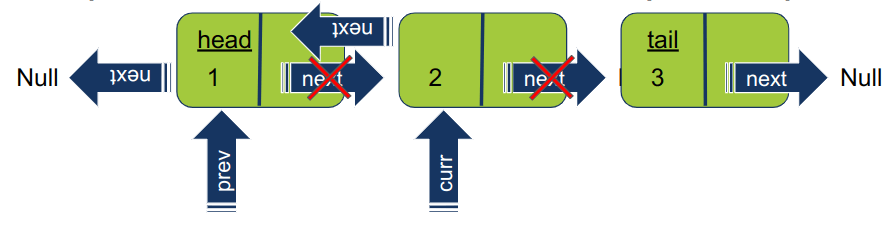
4. חוזרים על אותו התהליך גם עבור האיבר הבא ברשימה. מזיזים את המצביעים curr ו-prev איבר אחד קדימה, ואז מפנים את המצביע של האיבר הנוכחי על האיבר הקודם. במקרה שלנו, איבר 3 עובר להצביע על 2.

   

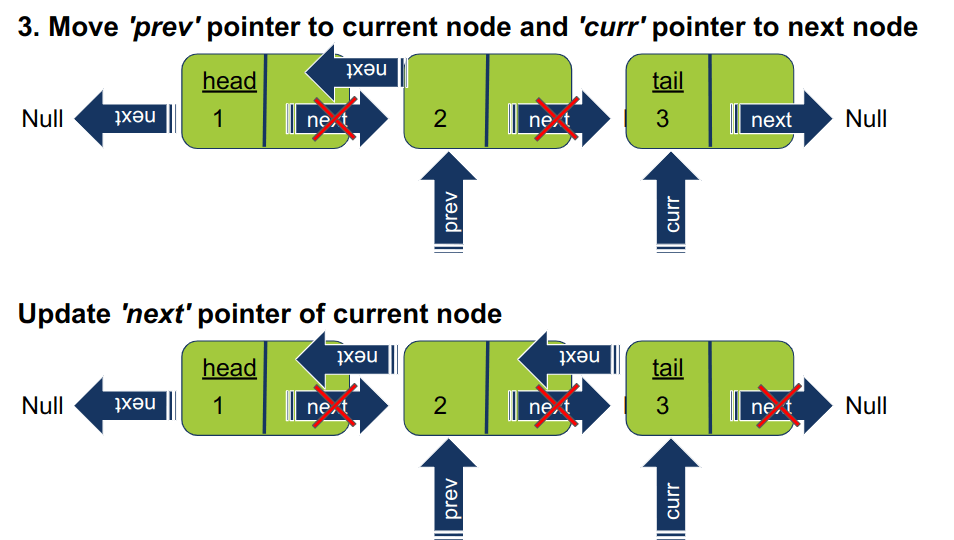
5. התהליך חוזר על עצמו גם כשמגיעים לאיבר האחרון ברשימה. מעבר לאיבר האחרון נמצא Null כשהמצביע curr מתקדם צעד נוסף הוא מקבל ערך Null דבר המסיים את האיטרציה.

   

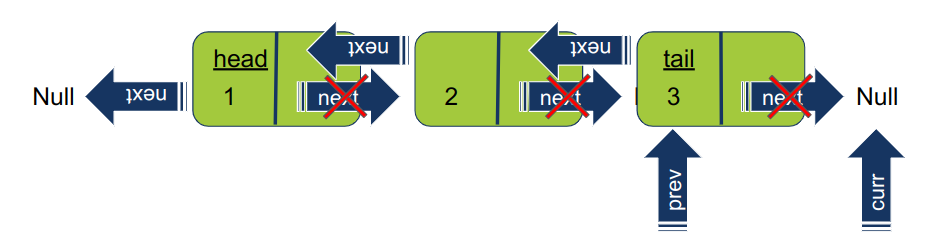
6. בשלב האחרון, מחזירים את ה-head של הרשימה ההפוכה.

האם פלינדרום?

פלינדרום הוא כל רצף - מילה, ביטוי, מספר - שניתן לקרוא אותו מההתחלה לסוף ומהסוף להתחלה ובכל זאת לקבל את אותו דבר. דוגמאות לפלינדרומים בעברית הם: "שמש", "לבלב", "מוּם תַּחַת מוּם", "ילד נתן דלי". באנגלית: "madam", "kayak", "racecar", "civic" או המשפט: "A man, a plan, a canal: Panama". אפשר גם בספרות: 7777 או תאריכים 11/11/11, 2/2/22

אפשר להשתמש בטכניקת שני המצביעים למציאת פלינדרומים. לשם כך נשתמש בטכניקת שני המצביעים בדרך מעט שונה כיוון שהמצביעים מתחילים מאמצע הרצף ומתקדמים לקצותיו במקום להתחיל בקצוות הרצף.

הקוד הבא מוצא האם מחרוזת היא פלינדרום באמצעות טכניקת שני המצביעים:

def is_palindrome(s = ""):
    """Determines if a given string is a palindrome."""
    string_length = len(s)
    
    # If the string has 0 or 1 characters, it's not a palindrome.
    if string_length < 2:
        return False
    
    # # Calculate mid-point and initialize pointers.
    mid = string_length // 2
    left_index = mid - (1 if string_length % 2 == 0 else 0)
    right_index = mid
    
    # Check characters at symmetric positions around the center.
    while left_index >= 0 and right_index <= string_length:
        # If characters don't match, it's not a palindrome.
        if s[left_index] != s[right_index]:
            return False

        # Proceed to next characters.
        left_index -= 1
        right_index += 1

    # All characters matched, it's a palindrome.
    return True

נבדוק:

# Even number of characters
print("'aa' is ", is_palindrome("aa")) # 'aa' is  True
print("'ae' is ", is_palindrome("ae")) # 'ae' is  False
print("'eaae' is ", is_palindrome("eaae")) # 'eaae' is  True
print("'eaam' is ", is_palindrome("eaam")) # 'eaam' is  False
print("'abcd' is ", is_palindrome("abcd")) # 'abcd' is  False

# Odd number of characters
print("'eae' is ", is_palindrome("eae")) # 'eae' is  True
print("'feaef' is ", is_palindrome("feaef")) # 'feaef' is  True
print("'feaem' is ", is_palindrome("feaem")) # 'feaem' is  False

# Known palindromes
print("'racecar' is ", is_palindrome("racecar")) # 'racecar' is  True
print("'hannah' is ", is_palindrome("hannah")) # 'hannah' is  True
print("'borroworrob' is ", is_palindrome("borroworrob")) # 'borroworrob' is  True

גישת שני המצביעים מפגינה סיבוכיות זמן לינארית O(N), כאשר N הוא אורך המחרוזת. הסיבה לכך היא שהאלגוריתם עובר לכל היותר חצי מחרוזת, תוך ביצוע השוואות בזמן קבוע בכל שלב. סיבוכיות המקום היא קבועה O(1) כיוון שהאלגוריתם משתמש בכמות קבועה של מקום ללא קשר לגודל הקלט היות וכל המשתנים בפונקציה אינם דורשים מקום נוסף בזיכרון.

בסה"כ השימוש באלגוריתם שני מצביעים לבירור האם רצף הוא פלינדרום הוא מאוד יעיל. האלגוריתם פשוט ואינטואיטיבי ואין דרישה למבני נתונים נוספים. כדי לראות כמה הוא יעיל אפשר להשוות עם הגישות לבירור האם רצף הוא פלינדרום באמצעות מבני הנתונים: stack ערימה או queue תור.

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

Linked list - רשימה מקושרת - תיאוריה, קוד ואתגרים תכנותיים

big-O ביטוי ליעילות הקוד

stacks, ערימות וחידות

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים