חוק בייס (bayes) וכללי אצבע לחיים
מה משותף לבדיקות קורונה, לזיהוי מטוסי אויב וזנים של כלבים? כולם דוגמאות להערכת הסתברויות בפעולה, והנטייה שלנו היא להסתמך מדי על האינטואיציה הראשונית בעניין. חוק בייס מסייע לנו להביא בחשבון מידע נוסף, ולעדכן את הערכת הסיכויים בהתאם להתפתחויות בשטח.
חוק בייס וזיהוי כלבים מגזע האסקי
אתמול הלכתי ברחוב וראיתי כלב חמוד. כשחזרתי הביתה סיפרתי בהתלהבות רבה על הכלב, ונאמר לי שהכלב הוא כלב מגזע האסקי כי ידוע ש-95% מכלבי ההאסקי הם חמודים. לאור מה שנאמר לי, עניין אותי לדעת מה הסיכוי שהכלב שפגשתי הוא אכן האסקי. אז בררתי באינטרנט וגיליתי ש-50% מהכלבים הם חמודים, וגם ש-5% מהכלבים שייכים לגזע ההאסקי.
ניתן לתאר את הנתונים באופן הבא:

ולהציג את ההסתברויות באמצעות הטבלה הבאה:
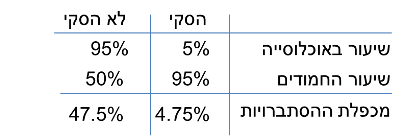
השורה האחרונה היא מכפלת ההסתברויות. נסביר את החישוב:
מה הסיכוי להאסקי חמוד?
5% X 95% = 4.75%
ומה הסיכוי לכלב חמוד שאינו האסקי?
95% X 50% = 47.5%
היחס של 4.75 ל47.5 הוא 1:10, כלומר הסיכוי שהכלב החמוד שראיתי הוא האסקי הוא נמוך. אבל כמה נמוך? לשם כך עלינו לחשב את גודל מרחב ההסתברויות שכולל סיכוי של 1 לכלב האסקי חמוד וסיכוי של 10 לכלב חמוד שאינו האסקי, כך שמרחב ההסתברויות הוא `1+10=11` , והסיכוי להאסקי מתוך מרחב ההסתברויות הוא `1:11`.
אפשר לכתוב את זה כך:
1/(1+10) = 1/11
מזה אנחנו יכולים ללמוד שכשמתחשבים בנתונים המקדימים (שיעור ההאסקי באוכלוסיית הכלבים) הסיכויים למסקנה שהכלב החמוד שפגשתי הוא אכן האסקי נמוכים. כי אם הייתי מתחשב רק בנתון ש-95% מכלבי ההאסקי הם חמודים הייתי עלול הייתי לחשוב שרוב הסיכויים שפגשתי האסקי, אבל בהינתן השיעור הנמוך של גזע כלבים זה באוכלוסיה הסיכויים דווקא גדולים יותר שהכלב החמוד שפגשתי אינו כלב האסקי.
מזה אפשר ללמוד שבכל פעם ששוקלים את הנתונים הקיימים בניסיון להבין את העולם צריך לנסות למצוא ולהתחשב בנתונים מקדימים. דבר שאנחנו כבני אדם נוטים לשכוח כשאנחנו מגבשים את דעתנו על המציאות.
כאמור, המסקנה שפגשתי האסקי התבררה כלא סבירה בהתבסס על הידע המקדים בדבר שיעור ההאסקי באוכלוסיה ושיעור הכלבים החמודים. אבל בהמשך התבררו לי עובדות שלא ידעתי ששינו את דעתי. לדוגמה, הכלב שפגשתי דומה לזאב וזה הגדיל את הסיכויים שמדובר בהאסקי (אם כי לא היווה עדות מכרעת כיוון שישנם גזעים נוספים שדומים לזאבים). אח"כ נזכרתי שהכלב שפגשתי הוא אתלטי וזה הגביר עוד יותר את הסיכויים שאכן פגשתי בהאסקי. ולבסוף, בביקורי בקוטב הצפוני ראיתי כלבים האסקים רתומים למזחלה שהם זהים בכל לכלב שפגשתי, וזה גרם לי לשנות את דעתי ולהסיק שהכלב שפגשתי הוא בסבירות של כמעט 100% כלב האסקי.
מהדוגמה הזו, אפשר להבין שאחרי גיבוש הדעה הראשונית, מנומקת ומחושבת ככל שתהיה, עדיין צריך לשמור על ראש פתוח לעדויות נוספות שיכולות לחזק את דעתנו או להחליש אותה. וכמו בדוגמה הזו, כך בחיים, צריך כל הזמן לחפש את המידע המקדים שיכול לשפוך אור חדש על המסקנות והאמונות שלנו.
הנוסחה של חוק בייס
אחרי שהבנו איך לעשות חישוב אינטואיטיבי של חוק בייס נסביר את הנוסחה עצמה. לא חייבים לקרוא את החלק הזה אם לא רוצים, ובהחלט אפשר לדלג ישר לפסקה הבאה כדי לראות דוגמאות נוספות לחישובים אינטואיטיביים אבל למי שכן רוצה יהיה עכשיו הרבה יותר קל להבין את הנוסחה שבסך הכול לוקחת בחשבון עדויות מהשטח כדי לעדכן את ההשערה הראשונית.
זו הנוסחה:
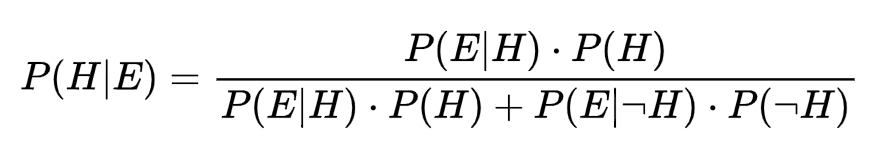
- P(H) - ההשערה הראשונית שלנו (prior). זה מה שאנחנו חושבים שהיא ההסתברות לפני החישוב. במקרה של הדוגמה עם ההאסקי ההשערה הראשונית שלנו היא שהכלב הוא האסקי ושיעור גזע זה באוכלוסיה הוא 5%.
- P(E|H) - ההסתברות לראות את מה שאנחנו מחפשים בהינתן שההשערה נכונה (Likelihood). במקרה שלנו, זה 95% כי זה שיעור החמודים מבין ההאסקים.
- P(~H) - החלק באוכלוסיה שאינו מתאים להשערה הראשונית (במקרה שלנו אילו כל הכלבים שאינם האסקים).
- P(E|~H) - השיעור של בעלי התכונה מבין מי שאינו מתאים להשערה הראשונית (שיעור החמודים מבין מי שאינם האסקים).
- P(E) - החלק באוכלוסייה שיש לו את התכונה המבוקשת מורכב מחיבור של P(E|H) עם P(E|~H) כלומר, כלל בעלי התכונה בין אם הם מתאימים להשערה ובין אם לא (במקרה שלנו, כל החמודים בין אם הם האסקים או שאינם).
- P(H|E) - תוצאת החישוב (posterior) זו הסתברות ההשערה H לאחר שלקחנו בחשבון את העדויות E.
נמלא את ערכי המשתנים לתוך הנוסחה לעיל:
-
ההיפותיזה (H) היא שהכלב שייך לגזע ההאסקי. נציין את שיעור גזע זה באוכלוסייה באמצעות:
שיעור ההאסקים P(H) = 0.05
שיעור מי שאינם האסקים P(~H) = 0.95 -
ההסתברות לחמוד אם הכלב הוא האסקי (E|H) = 0.95
-
ההסתברות לחמוד אם הכלב אינו האסקי (E|~H) = 0.5
נציב בנוסחה, ונפתור:
P(E|H) = (P(E|H)*P(H)) / (P(E|H)*P(H) + P(E|~H)*P(~H)) P(E|H) = (0.95*0.05) / (0.95*0.05 + 0.5*0.95) = 1/11
-
התוצאה אותה קיבלנו מהצבה בנוסחה זהה לזו שקיבלנו באמצעות חישובים אינטואיטיביים.
בדרך כלל' נראה את הנוסחה המקוצרת שבה כל החלק של האוכלוסייה שיש לו את התכונה נמצא במכנה P(E):
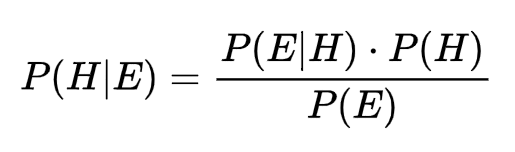
- נוסחה זו שקולה לנוסחה הקודמת. הסיבה בגללה בחרתי להציג קודם את הנוסחה בגרסתה המלאה יותר היא שדרך ההצגה המפורשת מקלה את ההבנה איזה נתונים יש להציב במכנה.
עכשיו שראינו את הנוסחה המלאה נסביר אותה במילים. ההשערה P(H) היא שהכלב הוא האסקי והעדות התומכת היא שהכלב חמוד P(E). אנחנו מחפשים את הסתברות ההשערה שהכלב הוא האסקי בהנתן העדות התומכת שהוא חמוד P(H|E). לצורך כך, אנו מביאים בחשבון את העובדה שהתכונה (חמידות) לא קיימת רק עבור החלק באוכלוסייה שמקיים את ההשערה (האסקי) אלא גם עבור החלק שאינו מקיים את ההשערה (לא האסקי).
זיהוי מטוסי אויב וכשלים בחשיבה
דמיין שאתה טייס בחיל האוויר הישראלי שמוזנק לטפל במטוס מיג שחדר לשמים האוויריים של ישראל מעל רמת הגולן. ידוע לך שלא רק חיל האוויר הסורי עלול לטוס באזור כי גם הרוסים טסים באזור, ואתם יש לנו יחסי ידידות. בנוסף, ידוע ששיעור מטוסי המיג הסורים באזור הוא 10%, ויתר המטוסים הם רוסים. וגם ששיעור הזיהוי הנכון על ידי טייסי חיל האוויר שלנו הוא 80%. מכיוון שטייס חיל האוויר זיהה את המטוס כמטוס סורי השאלה הרת הגורל היא מה מידת הביטחון שבה הוא יכול להחליט להפיל את המטוס?
התשובה האינטואיטיבית היא שאם מידת הזיהוי הנכון היא 80% אז זו גם צריכה להיות מידת הביטחון בהחלטה להפיל את המטוס. רק שאם נתחשב רק בתחושת הבטן נתעלם מהנתון הנוסף שהוא שיעור המטוסים הסוריים מכלל מטוסי המיג בזירה.
נכניס את כל הנתונים לתוך המטריצה הבאה שתסייע לנו לחשב את ההסתברויות תוך התחשבות בפרופורציה של המטוסים בזירה.

נכפול את ההסתברויות:
| זיהוי נכון (80%) |
זיהוי שגוי (20%) |
|
|---|---|---|
| סורי (10%) |
סורי באמת (80% * 10% = 8%) |
סורי שמזוהה כרוסי (10% * 20% = 2%) |
| רוסי (90%) |
רוסי באמת (90% * 80% = 72%) |
רוסי שזוהה כסורי (90% * 20% = 18%) |
ממכפלת ההסתברויות אנחנו למדים שהסיכוי שהמטוס שזוהה כסורי הוא אכן כזה הוא 8%, והסיכוי לזהות מטוס רוסי בטעות כסורי הוא 18%. לפיכך, הסיכוי לזיהוי נכון הוא 8 ל-18. או 8 מתוך 26 (8 + 18 =26). כלומר, הסיכוי שהמטוס שזוהה כסורי הוא באמת מטוס אויב שצריך להפיל אותו הוא פחות מ-31%.
הנטייה של רוב האנשים לבחור במידע שהכי פשוט להבין ולהתבסס עליו בהסקת המסקנות שלהם, מכונה שגיאה בשיעור הבסיס (base rate fallacy), והיא אחראית לרבים מכשלי החשיבה והמסקנות השגויות שאנשים נוטים ליפול לתוכם.
האם יש לך קורונה במידה ויצאת חיובי בבדיקה המהירה?
באחד הימים, חשת עייפות, וגילית שיש לך חום קל, מה שגרם לך לחשוד שאולי אתה סובל מקורונה. נסעת לבית המרקחת ורכשת בדיקת קורונה ביתית שהתוצאה שלה הייתה חיובית, והעידה על כך שנדבקת בנגיף. על הקופסה קראת ששיעור הזיהוי הנכון במקרה שאדם סובל מהנגיף הוא 99% וגם ששיעור הלא חולים המזוהים כחולים בטעות עומד על 1%.
רגע אחרי הגילוי, ולפני שאחזה בך הבהלה, עצרת ונזכרת בחוק בייס, ותהית אם כבר להיות מבוהל אז עד כמה.
מכיוון שאתה זוכר את חוק בייס אתה מנסה לברר מה שיעור הבסיס כאשר שיעור הבסיס הוא שיעור הנדבקים בקורונה באוכלוסייה. חיפוש מהיר בגוגל מעלה ש-1% מאוכלוסיית ישראל נדבק במחלה.
בהינתן המידע, האם להאמין לתוצאות הבדיקה ולהכניס את עצמך לבידוד?
חישוב זריז:
חולים שהערכה מזהה נכונה:
0.99 * 0.01 = 0.0099
מזוהים כחולים למרות שאינם:
0.01 * 0.99 = 0.0099
ממכפלת ההסתברויות אפשר לראות שהסיכוי שהאדם אינו חולה במחלה למרות הזיהוי החיובי בבדיקה זהה לסיכוי שהוא חולה והערכה זיהתה את מחלתו. כך שכדאי למהר ולהבדק על ידי גורם מוסמך, ובינתיים להיכנס לבידוד כדי לקטוע את שרשרת ההדבקה.
אבל מה היה קורה אילו 40% מהאוכלוסייה היה נדבק במחלה?
חישוב זריז:
חולים שהערכה מזהה נכונה:
0.99 * 0.4 = 0.396
מזוהים כחולים למרות שאינם:
0.01 * 0.6 = 0.006
כאשר 40% מהאוכלוסייה חולה במחלה הסיכוי שמי שהערכה מזהה כחולה הוא אכן חולה הוא:
0.396 / (0.396+0.006) = 0.985
כאשר 40% מהאוכלוסייה חולה במחלה הסיכוי שמי שהערכה מזהה כחולה הוא אכן חולה קרוב ל-99%.
מה קרה פה? איך קפצנו מ-50% זיהוי נכון במידה והמחלה הדביקה 1% מהאוכלוסייה לכמעט 99% כשהמחלה הדביקה 40% מהציבור? זו חשיבות שיעור הבסיס. ככל שפוחת שיעור בעלי התכונה באוכלוסייה, כך בדיקה שאינה ודאית עלולה לשגות ולייחס את התכונה גם למי שאין לו אותה.
אז מה עושים? בדיקה נוספת עצמאית, ואם גם בה התוצאה חיובית אז הסיכויים לשגיאה בזיהוי הם מאוד נמוכים.
הסתכלות סטטיסטית ברוח חוק בייס על הפרשה שמסעירה את המדינה
הנושא של חטיפת ילדים בקום המדינה מעסיק ומזעזע את הציבור הישראלי עד ימינו. הרבה שנים סברתי שהמידע החסר היה שיעור תמותת התינוקות בקום המדינה, ושלעובדה שבימינו תמותת תינוקות היא אירוע נדיר יש השפעה על הבנתנו את הנושא. חיזוק לדעתי, מצאתי באינטרנט בנתון שלפיו שיעור תמותת התינוקות בשנה הראשונה לחייהם באירופה עד שנות ה-50 של המאה ה-20 היה 50%, ולכן חשבתי שניתן להסביר את העלמות חלק גדול מהילדים בפטירתם בנסיבות טבעיות. הגעתי למסקנה זו כי הקשבתי פחות לעדויות של ההורים שאיבדו את ילדיהם, וחיפשתי עובדות אובייקטיביות.
ברבות השנים, נתקלתי בעדויות שערערו את תפיסתי את הנושא. לדוגמה, אישה בשם ציונה מספרת שהיא הובאה "מתנה" להורים המאמצים שלה. זה גרם לי לחשוב שאולי מדובר במקרה בודד ויוצא דופן. כעבור מספר שנים נתקלתי באתר ynet בעדות מצולמת ומוקלטת, של מטפלת שטפלה בילדים ומספרת שילדים נעלמו מעריסותיהם לאחר ביקורים של נשים מחו"ל. זה גם מצטרף לכך שלרבים מהילדים אין קבר. והמסקנה שלי היום, בעקבות העדויות הנוספות, היא שמאוד יכול להיות שלפחות חלק מהילדים שנעלמו אכן נחטפו.
* הכותב אינו מרביע כלבים, טייס, עוסק באיחוד משפחות או מומחה לבריאות הציבור. תיאורי המקרה והמספרים מיועדים להדגים את השימוש בחוק בייס ולא מעבר.
מקורות
Biases in Estimating Probabilities, Richards J. Heuer, Jr.
קריאה נוספת
10 הטיות קוגנטיביות שאתה חייב להכיר
רשימה לא ממצה של שגיאות לוגיות
אולי כן, אולי לא, עוד נראה (אגדה סינית עתיקה)
- פורסם לראשונה ב-
- ב- התווספה הדוגמה של הקורונה והנוסחה המפורשת
- ב- הרחבתי את ההסבר אודות נוסחת בייס
אהבתם? לא אהבתם? דרגו!
0 הצבעות, ממוצע 0 מתוך 5 כוכבים



הכותב הוא מתכנת שבמעט הזמן הפנוי העומד לרשותו נהנה לקרוא ספרים ולרשום לעצמו רשימות כדי להזכר במה שחשוב. מי שרוצה לחוות את דעתו מוזמן להוסיף תגובה ואשתדל לפרסם בהקדם.