המאזן בין הטייה bias ושונות variance בלמידת מכונה

אנחנו כל הזמן מנסים לשפר את ביצועי המודלים של למידת מכונה איתם אנו עובדים. לשם כך אנחנו משתמשים בכל מיני טכניקות. לדוגמה, אנחנו מנסים לשפר את איכות הנתונים או לבחור את המודל המתאים ביותר לבעיה. מאחורי כל מה שאנחנו עושים כדאי שתהיה הבנה של המאזן בין הטייה bias לבין שונות variance. כי הבנת המאזן תלמד אותנו מה לעשות כדי לשפר את התוצאות.

תיאור מקרה

נתונים שנאספו עבור מודל לחישוב מחיר בתים (בש"ח) על סמך שטח (במ"ר) נראים כך:

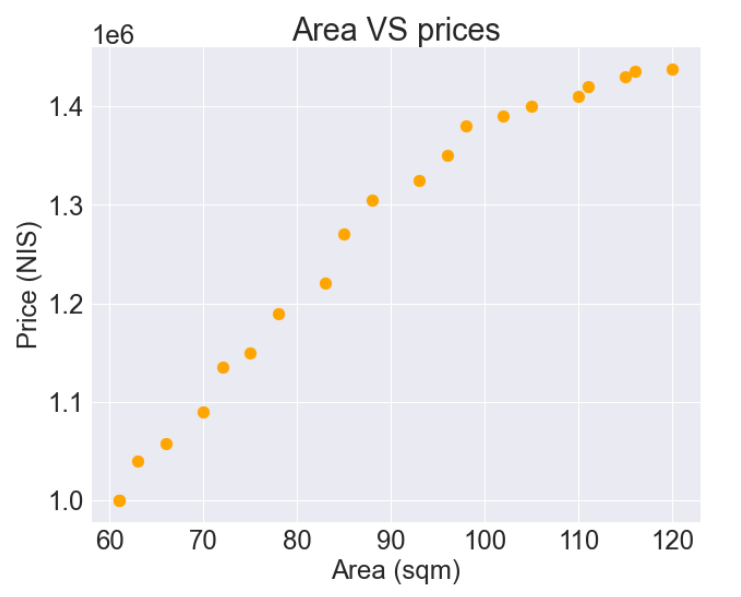
• דירות גדולות נמכרות במחיר גבוה יותר.
• הקשר בין מחיר ועלות הוא ליניארי עד שטח של 100 מ"ר ועבור דירות גדולות יותר תוספת המטרים משפיעה באופן מתון יותר על עליית המחיר.

מטרת המחקר הייתה לפתח מודל של למידת מכונה המסוגל לחשב את מחיר הדירה על סמך השטח שלה.

החוקר פיצל את המידע לשתי קבוצות: קבוצת אימון train set וקבוצת מבחן test set היות ומודלים של למידת מכונה לומדים מקבוצת האימון ובוחנים את יכולת הניבוי על קבוצת המבחן.

החוקר השתמש בשני מודלים שונים של למידת מכונה.

המודל הראשון רגרסיה לינארית אשר התאימה את הקו הישר הבא לקבוצת האימון:

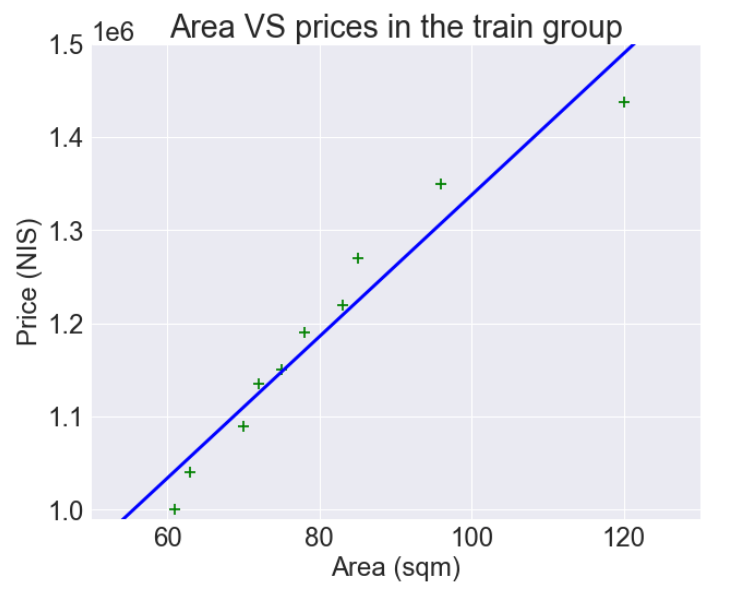
• הקו הכחול הוא התחזית של המודל לגבי מחירי הדירות.

המודל מבוסס הרגרסיה הלינארית אינו גמיש מספיק כדי לתאר את העקמומיות של הנתונים כי הוא יודע להתאים קו ישר אך לא מעוקל.

חוסר היכולת של מודל למידת מכונה (דוגמת רגרסיה לינארית) לתאר את נתוני קבוצת האימון נקרא הטייה bias.

אנחנו יכולים למדוד את מידת הסטייה של חיזויי המודל מן הנתונים על פי סכום הריבועים (sum of squares) אשר מודד את המרחק מהקו לנקודות מידע, מעלה בריבוע, וסוכם. 

המודל השני של למידת מכונה התאים קו מעוקל לסט נתוני האימון:

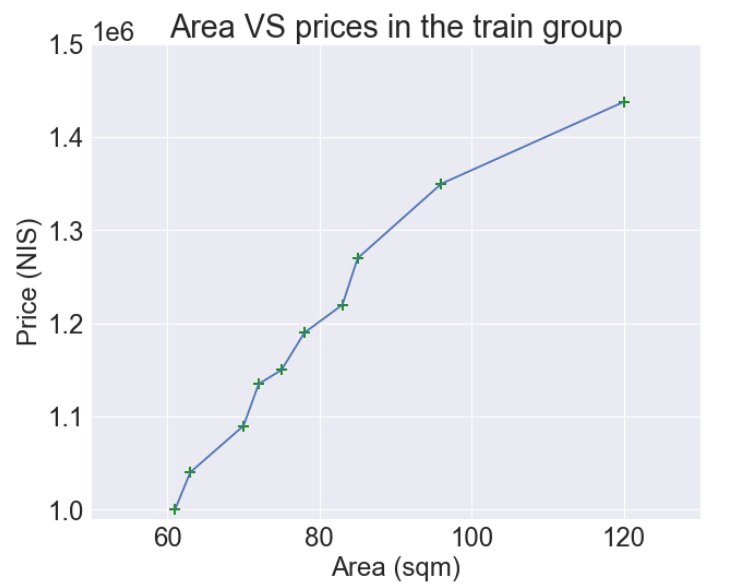
• הקו המעוקל גמיש מספיק כדי להתאים את עצמו בדיוק לתפזורת הנקודות במרחב.
• בגלל היכולת של הקו המעוקל לתאר בכזה דיוק את הנתונים יש לו הטייה bias נמוכה.
• סכום הריבועים ממש נמוך, ולמעשה שווה ל-0 כי ההתאמה היא מלאה.

עד עכשיו, נראה שיש לנו מנצח ברור. המודל השני שיודע לייצר קו מעוקל המתאים בדיוק לנתוני קבוצת האימון.

אבל בוא נראה מה קורה כשאנחנו מנסים את המודל על סט נתוני המבחן:

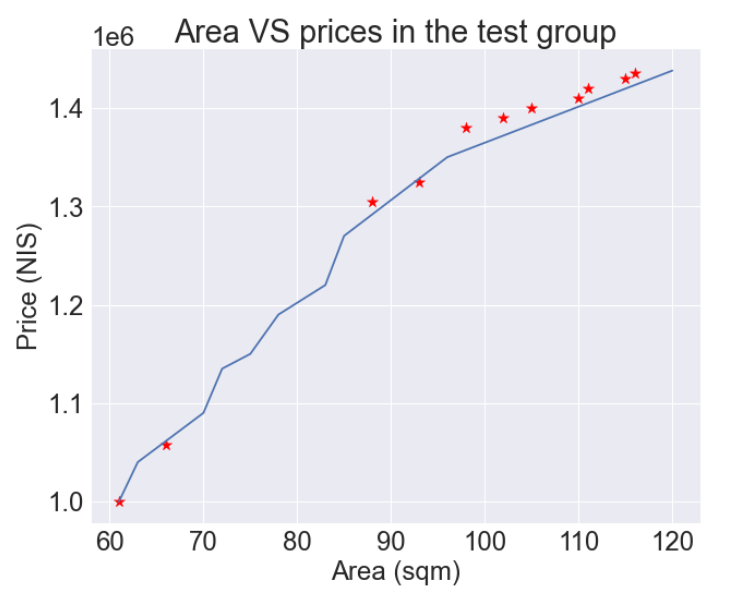
המודל שהתאים את עצמו בדיוק לקבוצת נתוני האימון לא מצליח למצוא אותה מידה של התאמה לנתוני קבוצת המבחן. השוני ביכולת החיזוי של המודל בין סטים של נתונים נקרא שונות variance.

לעומתו, המודל הראשון הפשוט, שהשתמש בקו ישר, מצליח להיות עקבי ולהגיע כמעט לאותה רמת דיוק אותה השיג בסט נתוני האימון גם עבור נתוני המבחן:

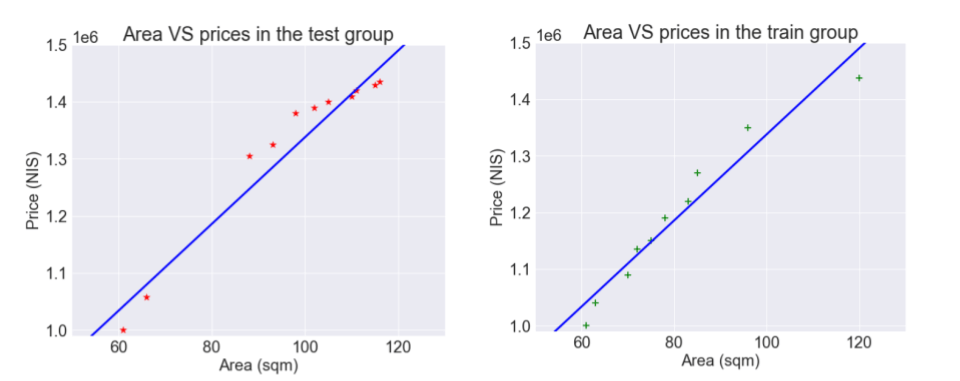
וזה בגלל שיש לו את אותה מידה של הטייה bias כלפי נתוני האימון והמבחן.

אז מה עדיף הטייה או שונות?

המטרה שלנו היא למצוא מודל שיש לו הטייה bias נמוכה וגם שונות variance נמוכה. במילים אחרות אנחנו רוצים מודל בעל יכולת הכללה. מודל שמסוגל להסיק מנתוני האימון כללים מספיק טובים כדי לספק תחזיות מדויקות עבור נתונים שאליהם הוא לא נחשף. אבל כמו שראינו אילו תכונות סותרות. לכן, השאיפה שלנו היא למצוא את נקודת האיזון שבה ההטייה והשונות יהיו הנמוכים ביותר. הנקודה הזו נמצאת במודל שהוא לא מסובך מדי ולא פשוט מדי. מודל מסובך במידה הנכונה.

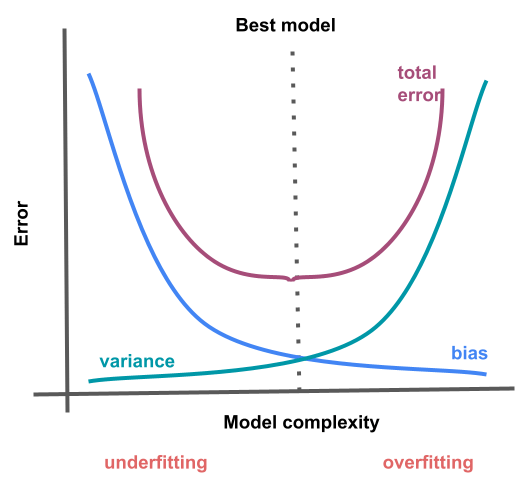
התאמת חסר והתאמת יתר

הקו הישר הוא מודל פשוט שלא מצליח להתאים לסט הנתונים ולכן יש לו הטייה bias גבוהה אבל יש לו שונות variance נמוכה בגלל שסכום הריבועים דומה בין סטים שונים של נתונים. במילים אחרות, המודל הפשוט מדי סובל מהתאמת חסר underfit. באנלוגיה, הוא מתנהג כמו תלמיד שלא למד מספיק ולא יודע את החומר למבחן.

נדע שהמודל שלנו סובל מ-underfit במידה ונגלה שהוא לא מצליח לחזות במידה סבירה את סט נתוני האימון וגם לא את המבחן.

מודל הקו המעוקל הוא מסובך. הוא אומנם מצליח להתאים את עצמו בדיוק לסט האימון אבל לא מצליח להכליל לדוגמאות המבחן. במילים אחרות המודל המסובך מדי סובל מבעיה של התאמת יתר overfit. המצב דומה לתלמיד שלמד יותר מדי למבחן ולכן יודע לדקלם את התשובות לשאלות עליהם התאמן אבל בגלל שהוא לא באמת מבין את החומר שינוי קל בניסוח השאלות יגרום לו לשגות.

נדע שהמודל שלנו סובל מהתאמת יתר overfit אם הוא מציג יכולת משמעותית יותר גבוהה על סט נתוני האימון מאשר על סט נתוני המבחן. כשצריך לשים לב, שכמעט תמיד ההתאמה תהיה טובה יותר לנתוני האימון, אבל הבדל משמעותי מעיד על התאמת יתר.

מצב לא שכיח הוא כאשר המודל מצליח יותר עם סט נתוני המבחן מאשר האימון דבר המעיד שיש בעיה במערך הניסויי. לדוגמה, ייתכן שהיתה דליפת נתונים (מסט האימון לסט המבחן), או שמספר הדוגמאות בסט המבחן הוא נמוך מדי. 

איך להגיע למודל הטוב ביותר?

עכשיו כשאנחנו יודעים שעלינו להימנע מהתאמת יתר וחסר, נלמד מה עלינו לעשות כדי להיחלץ ממצבים אילה.

דרך אחת להתמודד עם התאמת חסר היא על ידי הגברת מספר הדוגמאות. כאשר מספר דוגמאות האימון נמוך, המודל יתקשה ללמוד, והתוצאה תהיה התאמת חסר. ככל שנגדיל את מספר הדוגמאות המודל יצליח ללמוד יותר, ומעבר לרמה מסוימת תוספת הדוגמאות כבר לא תשפר את הלמידה.

מקור נוסף להתאמת חסר הוא מחסור בתכונות. לדוגמה: ניסיון לחזות מחירי דירות שלוקח בחשבון רק את גודל הבתים ומתעלם ממצבה הכלכלי של השכונה. אם זה המצב, כדאי לך להוסיף נתונים נוספים ובתנאי שהם רלוונטיים. מצד שני, עודף מידע לא רלוונטי עלול לגרום להתאמת יתר. לדוגמה, מודל לחיזוי מחירי בתים שלוקח בחשבון גם את צבע המכוניות המועדף והאם ילדי השכנים אוהבים ארטיק לימון. תפקיד עיקרי שלך בתור מומחה למידת מכונה הוא להצליח להיפטר מאותם גורמים המהווים מקור הפרעה ולהישאר רק עם המידע הרלוונטי ביותר.

כשהגעת לרוויה המתבטאת בכך שהוספת דוגמאות כבר לא תורמת לשיפור המודל ואין כבר מידע לא רלוונטי שממנו אתה יכול להיפטר, אתה יכול לעבור למודל בעל רמת סיבוך גבוהה יותר. לדוגמה, במקום מודל לינארי, מודל פולינומי מסדר גבוה. כשאתה מגיע לרמת סיבוך גבוהה מדי המתבטאת בהתאמת יתר, אתה יכול להפחית אותה על ידי שימוש בשיטות כדוגמת רגולריזציה, boosting או bagging.

באופן מעשי, את הפרמטרים למודלים מוצאים באמצעות פונקציות חיפוש דוגמת: Grid Search שמאתרת את הרכב הפרמטרים של המודל שמשיג את התוצאות הטובות ביותר. 

אחרי שמצאת את הפרמטרים הטובים ביותר למודל, מקור עיקרי להתאמת יתר הוא כאשר מריצים את המודל מספר גדול מדי של פעמים (יותר מדי epochs). הפתרון המעשי הוא שימוש בפונקציות שעוצרות את התהליך בשלב בו המודל מפסיק להתקדם.

לכל המדריכים בנושא של למידת מכונה

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים