התפלגות בטא ותהליך העדכון הבייסיאני

הרבה פעמים אנחנו משתמשים בסטטיסטיקה על מנת לייצר מודל של אי ודאות לגבי הסתברויות - בין אם זה הסיכוי של מטבע לנחות על ראשו או שיעור ההצלחה של קמפיין שיווקי. התפלגות בטא, התחומה לרוב בין הערכים [0,1], היא בחירה טבעית עבור משימות אילו. מדריך זה יוליך את הקורא בנתיב המוביל להתפלגות בטא, יסביר את מקרי השימוש בה, יציג עדכון בייסיאני כמסגרת לבחינת הסתברויות, ויסיים בדוגמה מעשית של קוד Python.

מברנולי לבינומי: קיצור תולדות ההתפלגות הבינומית

הסיפור מתחיל בהתפלגות ברנולי, המטפלת בניסוי יחיד עם שתי תוצאות אפשריות. לדוגמה, הטלה של מטבע. או שהמטבע נופל על "עץ" או שנופל על "פלי".

כאשר עושים מספר ניסויים עצמאיים של ברנולי, המספר הכולל של ההצלחות מתואר על ידי התפלגות בינומית. לדוגמה, הטלה של מספר מטבעות.

התפלגויות בסיסיות אילה משמשות לתיאור תהליכים בינארים, ומהוות בסיס להתפלגות בטא.

התפלגות בטא

התפלגות בטא נכנסת לתמונה כאשר מחלקים את מספר ההצלחות (והכישלונות) במספר הכולל של הניסויים דבר המעביר את המיקוד מספירת הצלחות לכימות אי הוודאות לגבי ההסתברות הבסיסית להצלחה אשר ערכה, כמו התפלגות בטא, תחום בין 0 ל-1. לדוגמה, ניסוי בהטלת מטבע כאשר "הצלחה" מוגדרת כקבלת "עץ". לאחר 10 הטלות, מתוכם 7 נפלו על "עץ" שיעור ההצלחה הוא 7/10=0.7 ושיעור הכישלון הוא המשלים ל-1, דהיינו 3/10=0.3.

התפלגות בטא מאופיינת בשני פרמטרים α ו-β שערכם נקבע על פי מספר ההצלחות והכישלונות:

Beta(α+1, β+1)

כאשר המוסכמה היא שיש להוסיף 1 לפרמטרים:

• למספר הצלחות מוסיפים 1 וזה הערך של α.
• למספר הכישלונות מוסיפים 1 וזה ערכה של β.

α ו-β קובעים את צורת ההתפלגות כפי שאפשר לראות בתרשים הבא:

• פונקצית הצפיפות (PDF) של הסתברות בטא מחושבת באמצעות הנוסחה:

  $$ f(x; \alpha, \beta) = \frac{x^{\alpha-1} (1-x)^{\beta-1}}{\int_0^1 t^{\alpha - 1} (1 - t)^{\beta - 1} dt} $$

  כאשר:

  • α ו-β קובעים את הצורה.
  • x מוגדר בטווח שבין 0 ל-1.
  • המכנה הוא פקטור מנרמל.

• השכיח mode מחושב באמצעות הנוסחה:

  $$ \text{Mode} = \frac{\alpha - 1}{\alpha + \beta - 2}, \quad \alpha, \beta > 1 $$

  והוא נמצא בערך המקסימום של הפונקציה.

• הממוצע מחושב באמצעות הנוסחה:

  $$ \text{Mean} = \frac{\alpha}{\alpha + \beta} $$

  והוא נוטה לעבר מרכז הכובד של הפונקציה. לדוגמה במקרה של 2,6 הוא יטה מעט ימינה מהשכיח בגלל שההתפלגות נוטה לימין.

• סטיית התקן קטנה ככל שמספר הדוגמאות גדול יותר דבר המעיד על ביטחון רב יותר בהערכה.

ככל שמצליחים לאסוף יותר נתונים ההתפלגות מצטמצמת כיוון שסטיית התקן קטנה ככל שהתוצאה מבוססת על מספר רב יותר של דוגמאות:

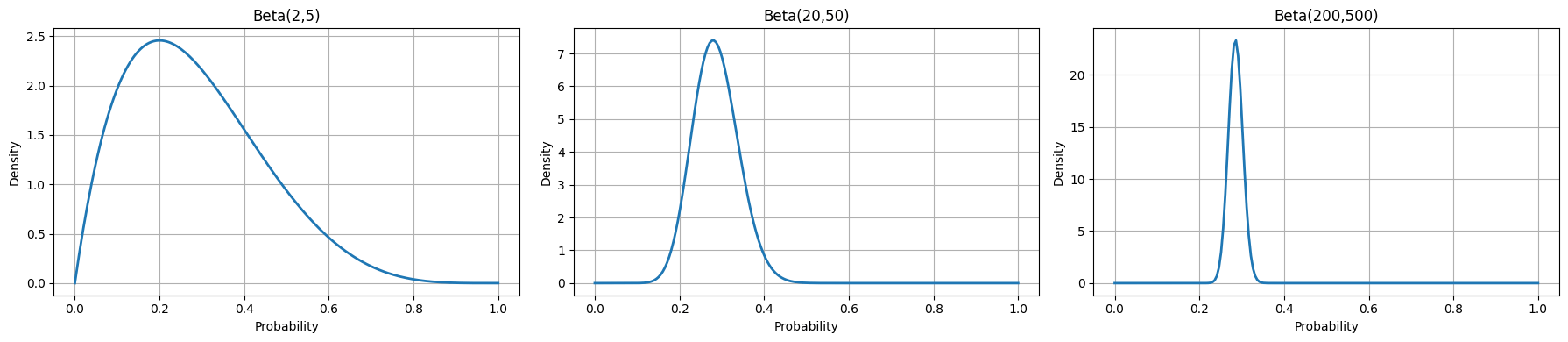
בהתפלגות בטא משתמשים, בין השאר:

• להערכת הסתברויות ופרופורציות: לדוגמה, הערכת שיעור ההצלחה של ניסויים קליניים או הפרופורציה של הקלקות על מודעה באינטרנט.
• להערכת משך זמן ביצוע: בניהול פרויקטים משתמשים בהסתברות כדי להעריך את משך הזמן הדרוש להשלמת משימות.

הסתברות בטא שימושית במסגרת של סטטיסטיקה בייסיאנית בגלל תכונות אותם נסביר בחלקו הבא של המדריך.

סטטיסטיקה בייסיאנית: מסגרת לעדכון אמונות בהינתן מידע חדש

מה שתהליך ההסקה הבייסיאני (Bayesian) עושה הוא לעדכן את האמונות הקודמות שלנו בהינתן ראיות חדשות. את התהליך נתחיל מהתפלגות מוקדמת, פריורית (prior), המייצגת את אי הוודאות הראשונית שלנו לגבי ההסתברות. בעקבות איסוף נתונים במסגרת ניסוי או מחקר מעדכנים את את המודל, אשר מפיק התפלגות מעודכנת, פוסטיריורית (posterior), המתחשבת בנתונים הראשוניים כמו גם בנתונים הנוספים.

העניין הוא שלא תמיד קל להפיק תוצאות שקל לעבוד איתם. יתרונה הגדול של התפלגות בטא כהתפלגות מוקדמת (פריורית) טמון בכך שההתפלגות הפוסטיריורית אשר מפיק המודל גם היא בטא מה שמקל על הפיתוח המתמטי ופירוש התוצאות. בזכות התכונה המאפשרת לקבל מתהליך העדכון הבייסיאני תוצאה השייכת לאותה משפחת התפלגויות ממנה מתחילים בטא קרויה התפלגות צמודה conjugate של סטטיסטיקה בייסיאנית.

למה התפלגות בטא מכונה "הסתברות של הסתברויות"?

כאשר אנו עוסקים בבעיות שבהן קיימת אי-וודאות לגבי ערך ההסתברות – למשל, ההסתברות שמטבע שאנחנו חושדים שהוא מוטה ינחת על "עץ" – אנחנו לא יודעים לנקוב בערך הסתברות אחד ספציפי. לגבי מטבע כזה אי אפשר להגיד "ההסתברות היא 0.5" כי אנחנו לא באמת יודעים אבל מה שאנחנו כן יכולים לעשות הוא לתאר את הסיכויים באמצעות התפלגות. במקרה של משתנה בינארי, התפלגות בטא,שהודות לה נוכל לאמר משהו דומה ל "יש לנו הסתברות מסוימת (למשל, 95%) שהערך המבוקש נמצא בטווח שבין 0.3 ל-0.7".

בפועל, במקום להצביע על ערך יחיד של הסתברות, לדוגמה 50%, מגדירים פונקצית הסתברות בה α ו-β מייצגים את הידוע לנו לגבי מספר ההצלחות והכשלונות. בכך, אנחנו למעשה יוצרים התפלגות על ערך ההסתברות – כלומר, אנחנו מתארים את ההסתברות באמצעות טווח x של הסתברויות. זהו הרעיון מאחורי הכינוי "הסתברות של הסתברויות".

כאשר אנו אוספים נתונים ומעדכנים את ההתפלגות בעזרת עדכון בייסיאני, אנחנו מצמצמים את חוסר הוודאות: עם נתונים מועטים, נקבל התפלגות רחבה. ככל שמצטברים נתונים, ההתפלגות מתרכזת, ומצביעה על ערך הסתברות מדויק יותר. כך, באמצעות התפלגות בטא, אנו לא רק מגדירים ערך נקודתי אלא גם מביעים את מידת אי הוודאות שלנו לגבי ערך ההסתברות.

דוגמה לתהליך עדכון בייסיאני

נניח שאתה בעל חנות רהיטים המעוניין לדעת האם אתר האינטרנט המושקע שלך יצליח למכור.

האפשרויות הם שמשתמש הנכנס לאתר שלך ירכוש ("הצלחה") או שלא ירכוש ("כישלון"). בגלל שלניסוי שאתה עורך יתכנו אחת משתי תוצאות זהו ניסוי בינומי, ולכן כדאי לך, כפי שכבר למדת, להשתמש בהתפלגות בטא לצורך עדכון מודל בייסיאני ממנו תלמד על סיכויי ההצלחה של האתר.

אתה לא באמת יודע כמה האתר שלך יצליח במשימה ולכן אתה משתמש בהתפלגות מקדימה (פריורית) "שטוחה" במסגרתה אתה מניח שמתוך 10 כניסות רק 5 ירכשו. זהו יחס של 5:5 בין הצלחה לכישלון מה שאומר:

Beta(α,β) = Beta(5+1, 5+1)

• תוספת של 1 לכמות הינה מוסכמה של שימוש בבטא עבור עדכון בייסיאני המתחיל מפריור שטוח (1:1).

עדכון המודל בפעם הראשונה: בשעה הראשונה אתה מגלה שנכנסו לדף 10 משתמשים מתוכם 4 רכשו בפועל. מה שאומר שיחס הצלחה לכישלון של 6:4. את הנתונים אתה מעדכן על ידי הוספה לפרמטרים הידועים מהצעד הקודם (5:5). לפיכך, ההתפלגות הפוסטיריורית תהיה:

Beta(α,β) = Beta(5+1+4, 5+1+6) = Beta(10, 12)

עדכון המודל פעם שנייה: בשעה השנייה אתה רואה שנכנסו לאתר 20 משתמשים ומתוכם 7 רכשו. יחס של 7:13. מה שאומר שבסך הכול, ולאחר הוספה לנתוני השלב הקודם, ההתפלגות הפוסטיריורית הינה:

Beta(α,β) = Beta(10+7, 12+13) = Beta(17, 25)

קוד פייתון ליישום תהליך העדכון הבייסיאני

קוד הפייתון להלן מחשב את המודל הבייסיאני אשר יסייע לסוחר להעריך כמה אתר האינטרנט שלו עשוי להצליח במכירת הרהיטים:

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta

# Define x values for plotting the Beta distributions (from 0 to 1)
x = np.linspace(0, 1, 200)

# --------------------------
# Step 0: Prior - Initial Prior Distribution
# We assume a flat prior with a 5:5 ratio.
# By convention, we add 1 to both counts:
#   alpha0 = 5 + 1 and beta0 = 5 + 1, resulting in Beta(6,6)
alpha0, beta0 = 5 + 1, 5 + 1  # Beta(6,6)
prior_pdf = beta.pdf(x, alpha0, beta0)

# --------------------------
# Step 1: First Update
# In the first hour, there are 10 visitors with 4 purchases.
# That gives 4 successes and 6 failures.
# We update our parameters by adding these counts:
#   alpha1 = alpha0 + 4  -> 6 + 4 = 10
#   beta1  = beta0 + 6   -> 6 + 6 = 12
alpha1 = alpha0 + 4   # 6 + 4 = 10
beta1  = beta0 + 6    # 6 + 6 = 12
update1_pdf = beta.pdf(x, alpha1, beta1)

# --------------------------
# Step 2: Second Update
# In the second hour, there are 20 visitors with 7 purchases.
# That gives 7 successes and 13 failures.
# We update our parameters again:
#   alpha2 = alpha1 + 7  -> 10 + 7 = 17
#   beta2  = beta1 + 13  -> 12 + 13 = 25
alpha2 = alpha1 + 7   # 10 + 7 = 17
beta2  = beta1 + 13   # 12 + 13 = 25
update2_pdf = beta.pdf(x, alpha2, beta2)

# --------------------------
# Plot the three distributions overlaid on the same diagram
plt.figure(figsize=(10, 6))
plt.plot(x, prior_pdf, 'b-', lw=2, label=f'Prior: Beta({alpha0}, {beta0})')
plt.plot(x, update1_pdf, 'g-', lw=2, label=f'First Update: Beta({alpha1}, {beta1})')
plt.plot(x, update2_pdf, 'r-', lw=2, label=f'Second Update: Beta({alpha2}, {beta2})')
plt.xlabel('Probability')
plt.ylabel('Density')
plt.title('Bayesian Updating: Overlaid Beta Distributions')
plt.legend()
plt.grid(True)
plt.show()

# --------------------------
# Print the parameters and the corresponding means for each stage
mean_prior   = alpha0 / (alpha0 + beta0)
mean_update1 = alpha1 / (alpha1 + beta1)
mean_update2 = alpha2 / (alpha2 + beta2)

print(f"Prior: Beta({alpha0}, {beta0}), mean = {mean_prior:.3f}")
print(f"First Update: Beta({alpha1}, {beta1}), mean = {mean_update1:.3f}")
print(f"Second Update: Beta({alpha2}, {beta2}), mean = {mean_update2:.3f}")

התוצאות מסוכמות בתרשים להלן:

נדפיס את הסטטיסטיקה עבור כל שלב:

# Print the statistics for each stage
print(f"Prior: Beta({alpha0},{beta0})")
print(f"  Mean = {mean_prior:.3f}")
print(f"  Mode = {mode_prior:.3f}")
print(f"  Std. Deviation = {std_prior:.3f}")
print(f"  95% Credible Interval = [{ci_prior[0]:.3f}, {ci_prior[1]:.3f}]
")

print(f"First Update: Beta({alpha1},{beta1})")
print(f"  Mean = {mean_update1:.3f}")
print(f"  Mode = {mode_update1:.3f}")
print(f"  Std. Deviation = {std_update1:.3f}")
print(f"  95% Credible Interval = [{ci_update1[0]:.3f}, {ci_update1[1]:.3f}]
")

print(f"Second Update: Beta({alpha2},{beta2})")
print(f"  Mean = {mean_update2:.3f}")
print(f"  Mode = {mode_update2:.3f}")
print(f"  Std. Deviation = {std_update2:.3f}")
print(f"  95% Credible Interval = [{ci_update2[0]:.3f}, {ci_update2[1]:.3f}]")

Prior: Beta(6,6)
  Mean = 0.500
  Mode = 0.500
  Std. Deviation = 0.139
  95% Credible Interval = [0.234, 0.766]

First Update: Beta(10,12)
  Mean = 0.455
  Mode = 0.450
  Std. Deviation = 0.104
  95% Credible Interval = [0.257, 0.660]

Second Update: Beta(17,25)
  Mean = 0.405
  Mode = 0.400
  Std. Deviation = 0.075
  95% Credible Interval = [0.263, 0.555]

ננתח את הממצאים

ככל שנאסוף יותר נתונים, ההתפלגות הפוסטיריורית ממתרכזת יותר – כלומר, הרווח בר המהימנות (Credible Intervals) קטן וסטיית התקן יורדת מה שאומר שאנו יכולים להיות בטוחים יותר בתוצאות הודות לצמצום חוסר הוודאות.

התכנסות וצמצום חוסר הוודאות

• בשלב הראשוני (Beta(6,6: כאשר השתמשנו בהתפלגות פריורית (6,6), אמונתנו לגבי שיעור ההצלחה הייתה מפוזרת באופן רחב – סטיית התקן הייתה 0.139 והרווח בר המהימנות היה בין 0.234 ל-0.766. משמעות הדבר היא שלא היינו מאוד בטוחים והתאפשר טווח רחב של ערכים.
• עדכון ראשון (Beta(10,12: לאחר שנאסף מידע אמיתי – 10 מבקרים עם 4 רכישות (4 הצלחות ו-6 כישלונות) – המרווח הצטמצם ל-[0.257, 0.660] וסטיית התקן ירדה ל-0.104. הנתונים החדשים עידכנו את האמונות הראשוניות שלנו.
• עדכון שני Beta(17,25): בשלב זה, תוספת נתונים – 20 מבקרים עם 7 רכישות (7 הצלחות ו-13 כישלונות) – חוסר הוודאות ירד עוד יותר: הרווח בר המהימנות הצטמצם ל-[0.263, 0.555] וסטיית התקן ירדה ל-0.075. כעת יש לנו הערכה מדויקת יותר של שיעור ההצלחה האמיתי.

שינוי בהערכות נקודתיות (ממוצע ושכיח)

• בתחילה: האמונת המוקדמת שלנו הייתה ממורכזת ב-0.5 כאשר הממוצע וגם השכיח (Mode) היו 0.5.
• לאחר איסוף הנתונים: הממוצע והשכיח פחתו – הממוצע ירד מ-0.455 ל-0.405, והשכיח מ-0.450 ל-0.400. זה מצביע על כך שהאמונה הראשונית הייתה מעט אופטימית ביחס לנתונים בפועל, וששיעור ההצלחה האמיתי נמוך יותר מהצפוי.

פירוש הרווח בר מהימנות  (Credible Intervals) 

בעקבות העדכון השני אנחנו יכולים להיותר בטוחים ב-95% שההסתברות האמיתית לכך שמבקר יבצע רכישה נמצאת בין 0.263 ל-0.555. טווח זה מעיד שאם נבצע ניסויים דומים בעתיד, ב-19 מתוך 20 פעמים נצפה בשיעור המרה בתוך טווח זה. ערכים קיצוניים מחוץ לטווח זה אמנם אפשריים, אך סביר שיהיו רק בכ-5% מהמקרים.

השלכות עסקיות

• אם נשתמש בנתונים אלו לחיזוי ביצועים עתידיים, ייתכן ונבחר להשתמש בממוצע (0.405) כהערכה נקודתית.
• כאשר מדובר בקבלת החלטות הדורשות זהירות (למשל, קביעת תקציבים לפרסום או הגדרת ציפיות הכנסה), אפשר להתמקד בגבול התחתון (0.263) כהערכה שמרנית.
• הגבול העליון (0.555) מציג תרחיש מיטבי, אך הסתמכות עליו בלבד עלולה להוביל להערכת יתר ולנטילת סיכונים מוגברת.

עדכונים עתידיים

• ככל שנמשיך לאסוף נתונים, צפוי שסטיית התקן והרווח בר המהימנות יפתחו עוד יותר, מה שיביא להערכות מדויקות יותר.
• שינוי בתנאי השוק (למשל, קמפיין שיווקי חדש) עשוי לשנות את ההתפלגות הפוסטיריורית.

מסקנות הניתוח

הלקח המרכזי הוא שככל שאנו אוספים יותר נתונים, חוסר הוודאות קטן וההערכות שלנו נעשות יותר מדויקות. מעבר לכך, חשוב לזכור שהדיווח הבייסיאני צריך לכלול לא רק הערכות נקודתיות (כמו ממוצע או שכיח), אלא גם טווחים של חוסר וודאות (דוגמת רווח בר מהימנות ברמה של 95%) – כך שמעניק תמונה מלאה של ה"סיכון" והביטחון בהערכות.

באופן זה, ניתן לקבל החלטות מושכלות תוך שקלול של כל ההסתברויות – מהתרחיש השמרני ועד לתרחיש האופטימי.

נסכם

ההתפתחות מהתפלגויות ברנולי ובינומיות להתפלגות בטא טומנת בחובה שינוי מהותי - מספירת הצלחות להבעת מידת אי הוודאות לגבי הסתברויות. המאפיינים של התפלגות בטא הופכים אותה לשימושית במיוחד בתחומים הנעים מבקרת איכות ועד לניסויים קליניים. באמצעות תהליך העדכון הבייסיאני, אתה יכול לדייק את ההערכות שלך ללא הרף, דבר המגביר את מידת הביטחון בתוצאה ככל שאתה מצליח לספק יותר נתונים. נסה את קוד ה- Python במדריך, וראה בעצמך כיצד התפלגות Beta מתפתחת בעקבות כל מידע חדש המוצב לתוכה.

מדריכים נוספים העשויים לעניין אותך

התפלגות בינומית - הלכה למעשה

מדריך מעשי על התפלגות פואסנית באמצעות קוד פייתון וציפורים נודדות

מבחני חי בריבוע לבדיקת השערות עם פייתון

לכל המדריכים בנושא של למידת מכונה

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים