שימוש באלגוריתם גנטי להתמודדות עם בעיה חישובית קשה במיוחד ממחלקת NP

אין דבר מהנה יותר ממציאת פתרון אלגנטי לבעיות תכנותיות. במיוחד אם הם קשות ומסובכות ופתרונם מצריך מאמץ רב. אולם קיימות בעיות תכנותיות שהם כל כך מורכבות עד שגם המחשבים החזקים ביותר מתקשים למצוא להם פתרונות בזמן סביר. בעיות אלו שייכות למחלקה NP - בעיות שאין להם פתרון דטרמיניסטי בזמן פולינומי.

דוגמה לבעיה מסוג NP היא בעיית התרמיל 0/1 אשר נחשבת לאתגר אופטימיזציה קלאסי. הבעיה דורשת למקסם את הערך הכולל תחת מגבלות משקל, והיא הולכת ומסתבכת ככל שגדל מספר הפריטים. הבעיה נובעת מכך שככל שגדל מספר הפריטים אותם ניתן להכניס לתרמיל, גדל מספר השילובים האפשריים באופן אקספוננציאלי כיוון שכל פריט מוסיף שתי אפשרויות (להכניס או להוציא), מה שמוביל ל-2^n שילובים פוטנציאליים עבור n פריטים. מורכבות אקספוננציאלית זו מאפיינת בעיות רבות השייכות למחלקה NP, שלא ידוע על אלגוריתמים יעילים למציאת פתרונות מיטביים עבורם.

כיוון שפתרון מיטבי של מקרים מרובי פריטים של בעיית התרמיל לא קיים למעשה, מומחי התכנות פונים לשימוש באלגוריתמים מקורבים שאף שאינם מבטיחים פתרונות מיטביים, הם כן מצליחים לספק תוצאות טובות למדי במסגרת טווחי זמן סבירים. דוגמה אחת היא שימוש באלגוריתם גנטי לצורך מציאת פתרונות מקורבים לבעיה.

אלגוריתמים גנטיים, שואבים השראה מתחומי האבולוציה והגנטיקה, ועושים שימוש במנגנונים של ברירה, שחלוף, ומוטציה כדי לאפשר לאוכלוסייה של פתרונות פוטנציאליים להתפתח לאורך דורות. בעוד שהפתרון האופטימלי אינו מובטח, אלגוריתמים אילה חוקרים ביעילות מרחבי פתרונות עצומים.

היישום במדריך של האלגוריתם הגנטי לבעיית התרמיל מדמה את האבולוציה של אוכלוסיות. הוא משלב אסטרטגיות כגון יצירת ושמירה על שונות, ברירת פרטים לפי מידת כשירות, יישום של שחלוף לצירוף חומר גנטי, והכנסת מוטציות לשיפור השונות. אסטרטגיות אילו, בדומה לתהליכים טבעיים, מנווטות במרחב החיפוש, ומתכנסות לפתרונות העומדים בדרישות הבעיה או לפחות מתקרבים לפתרון אופטימלי.

שיפורים נוספים, כולל אליטיזם והתאמה דינמית של שיעורי השחלוף, נועדו לשפר את ביצועי האלגוריתם. בנוסף, המדריך ידגים קריטריוני התכנסות כדי לקבוע מתי האלגוריתם הגנטי צריך לסיים לחקור עקב תשואה פוחתת של השיפור במידת הכשירות במעבר בין הדורות.

שלבי האלגוריתם הגנטי

האיור הבא מתאר את התפתחות הפתרון כאשר משתמשים באלגוריתם גנטי:

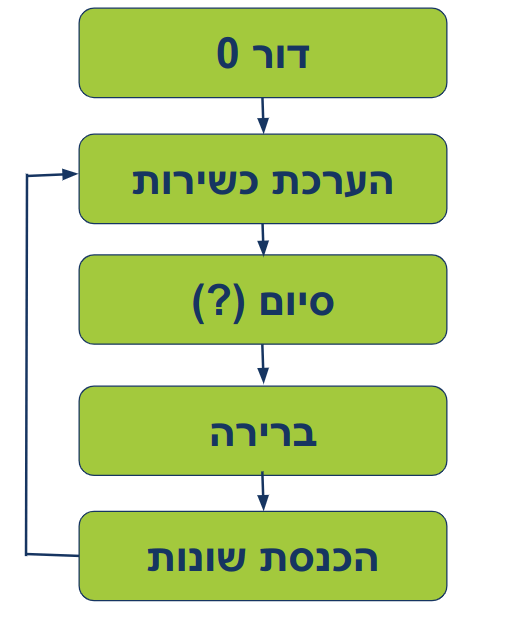
התהליך האבולוציוני מתחיל בהיווצרות האוכלוסייה במסגרת דור 0. קבוצה ראשונית זו של פרטים, מין "אורגניזמים" חישוביים, מייצגת פתרונות אפשריים לבעיה אותה מנסים לפתור. כל פרט נושא מטען גנטי, מחרוזת נתונים שמגדירה את מאפייניו ומשפיעה על הישרדותו במרוץ האבולוציוני.

בשלב השני נכנסת לפעולה לולאת הדורות בה מתקיים החיפוש של האלגוריתם אחר פתרונות מיטביים. לולאה זו מורכבת מ-4 שלבים שכל אחד מהם ממלא תפקיד חיוני בהתפתחות האלגוריתם האבולוציוני:

1. הערכה כשירות: בדומה לטבע, שבו ההישרדות תלויה בכשירות, כל פרט באוכלוסייה מקבל ציון כשירות המבוסס על יכולתו לפתור את הבעיה. ציון זה משמש להערכת מידת "זכאות" הפרט להעביר את המטען הגנטי שלו לדורות הבאים.

2. סיום/התכנסות: בשלב זה, האלגוריתם בודק האם לסיים או להמשיך לרוץ על סמך קריטריון עצירה, כדוגמת הגעה למספר מרבי של דורות או הפסקת התקדמות, כאשר שיפור הכשירות לאורך מספר דורות מדשדש, האלגוריתם יפסיק לרוץ.

3. ברירה: כאן נכנס העיקרון הדרוויני של "הישרדות הכשירים ביותר" לפעולה. התוצאה של הברירה היא שפרטים שקיבלו ציוני כשירות גבוהים יותר ייבחרו בסבירות גבוהה יותר כהורים לדור הבא. מנגנון זה מבטיח שתכונות רצויות יתפשטו, וימשכו בהדרגה את האוכלוסייה לכיוון פתרונות טובים יותר. תוכניות ברירה שונות, כמו ברירה פרופורציונלית וברירת טורניר, מציעות אסטרטגיות שונות לבחירת הורים כשירים.

4. הכנסת שונות (מוטציה ושחלוף): דומה למוטציות טבעיות ושחלוף גנטי המכניסים שונות באוכלוסיות ביולוגיות. מוטציות נקודתיות משנות באופן אקראי ביטים בודדים בתוך המטען הגנטי, מה שמגביר את הסיכוי לשיפורים בלתי צפויים ולמניעת התכנסות מוקדמת. מנגנון חשוב לא פחות הוא שחלוף אשר גורם לשילוב מקטעי חומר גנטי אקראי משני הורים, ויוצר צאצאים שהם שילוב של ההורים, שעשויים לקבל בירושה את החוזקות של אותם ההורים. שילוב חיוני זה של חקירה וניצול מאפשר לאלגוריתם לנווט במרחב הפתרונות העצום בצורה יעילה ביותר.

התהליך המחזורי הכולל: הערכה, ברירה והכנסת שונות עשוי לשפר את האוכלוסייה, ולדחוף אותה בהדרגה לעבר פתרונות הנהנים מכשירות גבוהה יותר. באופן אידיאלי, לאורך הדורות, כשירותה הממוצעת של האוכלוסייה גדלה ומחפשת להתקרב לפתרון מיטבי.

האלגוריתם הגנטי מחקה את היופי והעוצמה של הברירה הטבעית, ומנצל את עקרונותיה לצורך ייעול פתרונות חישוביים.

הסבר בעיית התרמיל 1 או 0

לחץ להורדת קובץ קלאס פייתון אלגוריתם גנטי שאותו נפתח במדריך

הגרסה שאני מכיר של בעיית התרמיל מספרת את סיפורו של יוסף, ארכיאולוג נועז החוקר תרבויות לא ידועות במרחבי הסייבר אשר תר אחר מקדש נסתר שהכניסה אליו חתומה בבעיות שאין איש או מחשב שיוכל לפותרן. יוסף, חמוש בתבונתו ובתרמיל בלבד נחוש לגלות את צפונותיו.

המקדש הזה לא מכיל זהב או תכשיטים. כי מה שנמצא בתוכו היא ספרייה, מדפיה עמוסים במגילות בהם ישנו ידע עתיק, שפות נשכחות וסודות שאבדו עם הזמן. כל מגילה מייצגת פיסת היסטוריה, הצצה לתרבות מפוארת שנעלמה.

המלכוד. התרמיל של יוסף יכול להכיל רק 6 ק"ג של כתבים עתיקים. כל חריגה תגרום לו להקרע וכל הידע העתיק יישאר על רצפת המקדש העתיק.

יוסף נאלץ לבחור בין:

כל מגילה עשויה לכתוב מחדש את ההיסטוריה, לעצב מחדש את העולם, או להציע כלים יקרי ערך לעתיד. אבל יוסף לא יכול לקחת את כולם. עליו לבחור את מטענו בזהירות, לאזן בתבונה בין משקל לערך.

האם הוא יעדיף את הידע על הכוכבים, או את סודות הרפואה? האם יבחר בניחוחות קולינאריים או בנפלאות השירה? האתגר מוגבל לא רק ביכולת הנשיאה של התרמיל, אלא בערך שניתן להפיק, כאשר כל מגילה מייצגת מסלול שטרם נחקר, סיפור שלא סופר.

אז, בעוד יוסף מתלבט בין הפוטנציאל האינסופי של הידע בקצות אצבעותיו ומשקל התרמיל על שכמו, השאלה המנקרת היא: מה יבחר יוסף לשאת החוצה מן המקדש?

גישה אחת לפתרון הבעיה משתמשת בכוח בלבד brute force לסריקת כל האפשרויות. במסגרת הגישה "הכוחנית" צריכים לבחון את כל האפשרויות, ומספר האפשרויות תלוי בכמות הפריטים. לדוגמה, אם אילו הם שני פריטים שניתן לבחור בין להוסיף לתרמיל או להשאיר בחוץ אז מספר האפשרויות על פי חוקי הקומבינטוריקה הוא: 2^2 = 4

אם 3 פריטים: 2^3 = 8.

אם 4 פריטים: 2^4 = 16.

כל פריט שנוסיף לקלט יכפיל את מספר הקומבינציות. בהתאם, אם נספק קלט של 10 פריטים אז נצטרך לבדוק יותר מ-1,000 צירופים. ואם 20 פריטים נהיה חייבים לבדוק יותר ממיליון קומבינציות.

במקרה של 50 פריטים, שתיכף ננסה לפתור, צריך לחקור 1.126X10^15 אפשרויות שזה מספר עם 15 אפסים אחריו או מיליון מיליארדים או קוואדריליון. שזה המון…

אפשר לראות גידול אקספוננציאלי של כמות החישובים ביחס לכמות הקלטים. קצב גידול שאותו נסמן באמצעות הנוטציה של big-o: O(2^N).

מה שאומר שהקוד לא יעיל. כל כך לא יעיל שאם ננסה לפתור באמצעות כוח בלבד את בעיית ה- knapsack, המחשב יחזיר את תוצאת החישוב עבור 77 פריטים רק אחרי מותה של מערכת השמש בעוד 5 מיליארד שנים. וזה בהנחה שיהיה מי שיזכור לברר את תוצאות החישוב.

האתגר כל כך מסובך שמומחי מחשב משייכים אותו למחלקה מיוחדת של בעיות, NP, ועד היום לא ידוע שום אלגוריתם שיכול לפתור את בעיות NP בזמן סביר עבור קלט ארוך.

קלאס פייתון ליישום אלגוריתם גנטי למציאת פתרון מקורב לבעיית התרמיל עבור מספר גדול של פריטים

בשביל ליישם את האלגוריתם הגנטי ניצור קלאס של פייתון `GeneticKnapsackSolver`:

class GeneticKnapsackSolver:
   def __init__(self, weights, values, max_weight, gen_number, population_size, mutation_rate, elite_size, convergence_threshold, convergence_generations, max_fitness):
       self.weights = weights
       self.values = values
       self.len_values = len(values)
       self.max_weight = max_weight
       self.gen_number = gen_number
       self.population_size = population_size
       self.mutation_rate = mutation_rate
       self.elite_size = elite_size
       self.convergence_threshold = convergence_threshold
       self.convergence_generations = convergence_generations
       self.best_results = []
       self.improvements = []
       self.max_fitness = max_fitness

הפרמטרים אותם מקבל הקלאס הם:

1. `weights`: רשימה המכילה את משקל הפריטים בבעיית התרמיל (Knapsack).
2. `values`: רשימה הכוללת את ערך הפריטים בבעייה.
3. `max_weight`: מגבלת המשקל של התרמיל שלאלגוריתם אסור לחרוג ממנו.
4. `gen_number`: מספר הדורות המקסימלי.
5. `population_size`: גודל האוכלוסייה בכל דור. כאשר האוכלוסייה מורכבת מפתרונות אפשריים (=פרטי האוכלוסייה) לבעיית התרמיל.
6. `mutation_rate`: אחוז הפרטים בכל סיבוב שיעברו מוטציה נקודתית.
7. `elite_size`: אחוז הפרטים בעלי הביצועים הטובים ביותר באוכלוסייה שיש להעביר ללא שינוי לדור הבא (אליטיזם).
8. `convergence_threshold`: ערך סף להתכנסות, כאשר השיפור יורד מתחתיו לאורך מספיק דורות (`convergence_generations`) נראה שהאלגוריתם לא עושה שיפורים משמעותיים ועל כן יש להפסיק את הריצה.
9. `convergence_generations`: מספר הדורות הרצופים עם שיפורים קטנים הדרושים כדי להפעיל התכנסות.
10. `max_fitness`: ערך יעד המייצג את הכשירות או הערך המקסימלי שהאלגוריתם מנסה להשיג. נשתמש בו להתאמה דינמית של שיעור השחלוף הגנטי crossover.

בדוגמה שלנו, צריך לבחור אילו פריטים נשים בתוך התרמיל מתוך אוסף פריטים. לדוגמה, אוסף של 5 פריטים המיוצגים באמצעות המערך: ['a', 'b', 'c', 'd', 'e']

כל פתרון שנבחן יהיה מערך של 5 ערכים בינאריים, 0 ו-1 כאשר 0 יציין פריט שנכנס לתרמיל, ו-1 פריט שיישאר מחוץ לתרמיל. לדוגמה: [1, 0, 0, 1, 1]

משמעו שהפריטים שיוכנסו לתרמיל יהיו: {'a', 'd', 'e'} בעוד {'b', 'c'} יישארו בחוץ.

בשביל לייצר את הפתרון נשתמש במתודה ליצירת פתרונות אקראיים:

def make_individual(self):
       # Generate a list of 1s and 0s representing a potential solution.
       # Each list item corresponds to a decision variable for the knapsack problem.
       # 1 indicates inclusion, 0 indicates exclusion.
       individual = [random.randint(0, 1) for _ in range(self.len_values)]

       return individual

• בכל פעם שנקרא למתודה `make_individual`, היא תחזיר מערך בינארי אקראי באורך מספר פריטי המערך (`len_values`) אשר יהווה פתרון אפשרי לבעיה.
• כל ערך שתחזיר הפונקציה הוא פתרון אפשרי וגם פרט באוכלוסייה.

המתודה `make_population` יוצרת את אוכלוסיית הדור הראשון, המורכבת מרשימה של פרטים. כל פרט באוכלוסייה מייצג פתרון אפשרי לבעיה. המתודה קוראת למתודה `make_individual` פעם אחת עבור כל פרט באוכלוסיה, וכך יוצרת קבוצה מגוונת של פרטים המהווים את האוכלוסייה הראשונית:

def make_population(self):
        # Generate a list of individuals, each representing a potential solution to the problem.
        # The population is a collection of these individuals.
        population = [self.make_individual() for _ in range(self.population_size)]
        return population

אוכלוסיית הדור הראשון היא אקראית לחלוטין. כדי לשפר את התוצאות נצטרך ליצור מנגנון סלקציה שיברור בין הפתרונות את המוצלחים ביותר כדי שיעברו לדור הבא.

Fitness כשירות הינה מדד עיקרי המשמש להערכה ודירוג של פתרונות בתוך האוכלוסייה, ומנחה את תהליך הברירה selection באלגוריתם הגנטי. פתרונות עם מידת כשירות גבוהה יותר סביר יותר שייבחרו לעבור לדור הבא, ובכפוף למנגנוני שחלוף גנטי ומוטציה, יזכו לתרום להתפתחות האוכלוסייה לאורך הדורות.

המתודה `fitness` מחשבת את מידת הכשירות של פתרון נתון באוכלוסייה. הערכה זו נעשית על ידי חישוב המשקל הכולל והערך הכולל של הפריטים הכלולים בתרמיל בכל פתרון נתון:

def fitness(self, solution):
    # Calculate the total weight of the solution using element-wise multiplication.
    solution_weight = sum(x * y for x, y in zip(solution, self.weights))

    # Calculate the total value of the solution using element-wise multiplication.
    calculated_fitness = sum(x * y for x, y in zip(solution, self.values))

    # Check if the total weight exceeds the maximum allowable weight.
    if solution_weight > self.max_weight:
        # If the weight limit is exceeded, assign a fitness score of -1 to indicate infeasibility.
        calculated_fitness = -1

    # Return the calculated total value as the fitness score for the feasible solution.
    return calculated_fitness

• המתודה מחשבת את המשקל הכולל והערך הכולל של הפריטים הכלולים בתרמיל בהתבסס על הייצוג הבינארי שמקורו במערך הקלט. אם המשקל הכולל עולה על המשקל המותר המקסימלי (`self.max_weight`), מידת הכשירות מוגדרת לערך הנמוך ביותר -1 כיוון שהפתרון אינו אפשרי. אחרת, הערך הכולל מוחזר כמידת הכשירות עבור הפתרון האפשרי.

המתודה `rank_individuals` מקבלת את אוכלוסיית הפתרונות כפרמטר ומדרגת את הפרטים לפי מידת הכשירות שלהם, מהגבוה לנמוך:

def rank_individuals(self, population):
        # Rank the individuals that make the population by how fit they are.
        ranked_individuals = [(self.fitness(individual), individual) for individual in population]
        ranked_individuals.sort(reverse=True)

        return ranked_individuals

• המתודה יוצרת רשימה של זוגות, כאשר כל זוג מכיל צמד מהצורה (`fitness`, `individual`) עבור כל פתרון באוכלוסייה. כאשר ציוני הכשירות מתקבלים על ידי קריאה למתודה `fitness` עבור כל פרט באוכלוסייה.
• רשימת הזוגות ממוינת לאחר מכן בסדר יורד לפי מידת הכשירות, באמצעות `ranked_individuals.sort(reverse=True)`.

מטרת דירוג הפרטים באוכלוסייה היא לתעדף את אלה המפגינים כשירות גבוהה יותר מה שמאפשר לאלגוריתם להתמקד בפרטים מבטיחים במרחב הפתרונות.

את רובה של הסלקציה לגבי אילו הורים יעבירו את המטען הגנטי שלהם לדור הבא עושה המתודה `fitness_proportionate_selection` אשר משתמשת בסלקציה מסוג "גלגל רולטה מוטה" biased roulette wheel. מה שאומר שפתרונות בעלי כשירות גבוהה יותר יזכו בסיכוי גבוה יותר לעבור כהורים לדור הבא:

def fitness_proportionate_selection(self, population):
        # Biased roulette wheel selection -
        # individuals with higher fitness have higher probabilities of being selected for the next generation

        # Extract fitness scores from the population
        fitness_scores = [fitness_score for fitness_score, _ in population]

        # Calculate the total fitness of the population
        total_fitness = sum(fitness_scores)

        # Calculate probabilities for each individual based on their fitness
        probabilities = [fitness / total_fitness for fitness in fitness_scores]

        # Select individuals using a biased roulette wheel with calculated probabilities
        selected_indices = random.choices(range(len(population)), weights=probabilities, k=len(population))

        # Retrieve the selected individuals based on their indices
        selected_individuals = [population[i] for i in selected_indices]

        return probabilities, selected_individuals

נסביר:

1. חילוץ ציוני כשירות: את מידת הכשירות fitness מחלצים עבור כל פריט באוכלוסיה מה שיוצר את הצמד (`fitness`, `individual`).
2. חישוב כשירות כוללת: הכשירות הכוללת של האוכלוסייה מחושבת על ידי סיכום סך כל הכשירויות באוכלוסייה.
3. חישוב הסתברויות: הסתברויות עבור כל פרט מחושבות על פי מידת הכשירות שלו. ככל שפרט כשיר יותר כך יגבר הסיכוי לבחור בו.
4. ברירת "גלגל רולטה מוטה" biased roulette wheel selection: ברירת הפרטים נעשית באקראי כאשר ההסתברויות שחושבו בשלב הקודם משמשות משקולות בהם מתחשבים לצורך הברירה. ככל שהכשירות גבוהה יותר, גדלה הסתברות הפרט לקחת חלק באוכלוסייה.

תוצאת התהליך היא קבוצה של פרטים שנבררו לעבור לדור הבא, עם הטיה כלפי אלו עם ציוני כשירות גבוהים יותר.

נוסיף מתודה להרצת קלאס האלגוריתם הגנטי:

def run(self):
       # Initialize the first generation
       population = self.make_population()
       # Rank solutions and choose the best for the next generation
       ranked_individuals = self.rank_individuals(population)
       _, selected_individuals = self.fitness_proportionate_selection(ranked_individuals)

       # Run the specified number of generations
       for gen_number in range(self.gen_number):
           # Generate the new generations based on the previous generation
           population = self.make_generation(selected_individuals)
           # Rank new solutions and choose the best for the subsequent generation
           ranked_individuals = self.rank_individuals(population)
           _, selected_individuals = self.fitness_proportionate_selection(ranked_individuals)

           # Record current generation results and track improvement
           selected_individual = selected_individuals[0]
           current_highest_fitness = selected_individual[0]
           current_highest_genetic_makeup = selected_individual[1]
           print(f"generation: {gen_number} * fitness: {current_highest_fitness} * selected_individual: {current_highest_genetic_makeup}")


           self.best_results.append((gen_number, current_highest_fitness, current_highest_genetic_makeup))

           if gen_number > 1:
               # Calculate improvement from the last generation.
               improvement = current_highest_fitness - self.best_results[-2][1]
               self.improvements.append(improvement)

           # Converge based on improvement criteria
           if gen_number >= self.convergence_generations and all(imp < self.convergence_threshold for imp in
                                                                 self.improvements[-self.convergence_generations:]):
               print("Converged!")
               break

נסביר:

בדור הראשון:

1. אתחול: את הדור הראשון של האוכלוסייה יוצרת המתודה `make_population`. בשלב זה חשוב ליצור אוכלוסייה גדולה ומגוונת מספיק.
2. דירוג ובחירה: מעריכים את כשירות fitness כל פרט באוכלוסייה, ופרטים מדורגים לפי מידת הכשירות שלהם. לאחר מכן, מתודת `fitness_proportionate_selection` משמשת לבחירת פרטים לדור הבא, תוך מתן עדיפות לאלה עם כושר גבוה יותר.

במסגרת לולאת הדורות:

1. לולאת דורות: הלולאה הראשית רצה לפי מספר הדורות שצוין (`gen_number`), יוצרת דור חדש ובוררת פרטים בכל פעם שהיא רצה.
2. יצירת דור חדש: המתודה `make_generation` אותה מיד נסביר נקראת בכל פעם ליצירת דור חדש המבוסס על הפרטים שנבררו מהדור הקודם.
3. דירוג הפרטים בתוך הדור הנוכחי וברירה: האוכלוסייה החדשה מדורגת, ופרטים נבחרים לדור הבא.
4. רישום תוצאות: בסיומה של כל איטרציה, תוצאות הדור הנוכחי, כולל ציון הכשירות הטוב ביותר והמבנה הגנטי, נרשמות ומודפסות.
5. בדיקת התכנסות convergence: האלגוריתם בודק התכנסות בהתבסס על קריטריוני השיפור. אם מידת שיפור הכשירות בדורות האחרונים נמוך מסף מסוים (`convergence_threshold`), ריצת הלולאה מופסקת.
6. ריצת הלולאה הראשית ממשיכה עד שמגיעים למספר הדורות המקסימלי או שמגיעים לכדי התכנסות.

את עיקר העבודה עושה המתודה `make_generation` שרצה בכל פעם שצריך לייצר דור חדש על בסיס דור קיים:

def make_generation(self, prev_gen):
        # List to store individuals for the new generation.
        population = []

        # Select a fixed percentage of the best individuals as elite
        elite_size = int(self.elite_size * self.population_size)
        elite_individuals = [ind[1] for ind in prev_gen[:elite_size]]

        # Calculate dynamic crossover rate based on the average fitness of the population.
        avg_fitness = sum(ind[0] for ind in prev_gen) / len(prev_gen)

        # Ensure the crossover rate (dynamic_crossover_rate) stays within a reasonable range of 0.2 to 1.0.
        # The value of `dynamic_crossover_rate` decreases as the algorithm approaches the maximum fitness (`max_fitness`).
        dynamic_crossover_rate = max(0.2, min(1.0, 1.0 - (avg_fitness / max_fitness)))
        print(f"dynamic_crossover_rate = {dynamic_crossover_rate}")

        # Perform crossovers to create children from pairs of parents.
        for _ in range((self.population_size - elite_size) // 2):
            # Select two parents from the previous generation.
            parent1 = self.get_parent(prev_gen)
            parent2 = self.get_parent(prev_gen)

            # Apply crossover with the dynamic crossover rate.
            if random.uniform(0, 1) < dynamic_crossover_rate:
                # Create two children by recombining the genetic material of the parents.
                child1, child2 = self.crossover(parent1[1], parent2[1])
            else:
                child1, child2 = parent1[1], parent2[1]

            # Add the children to the current generations population.
            population.extend([child1, child2])

        # Mutate random individuals in the population.
        mutated_indices = self.pick_mutated_indices()
        for idx in mutated_indices:
            population[idx] = self.mutate(population[idx])

        # Combine elite individuals with the offspring
        population.extend(elite_individuals)

        # Return the new generation of individuals.
        return population

נסביר:

1. בחירת עילית: אחוז קבוע של הפרטים הכשירים ביותר (`elite_size`) מהדור הקודם נשמר בצד בלי לעבור שינויים גנטיים (שחלוף ומוטציה) ומועתק ישירות לדור הבא כי אם כבר מצאנו פתרון טוב במיוחד אנחנו מעוניינים לשמור עליו.
2. חישוב דינמי של שיעור השחלוף crossover: שיעור השחלוף הדינאמי (dynamic_crossover_rate) מחושב על פי הכשירות הממוצעת של האוכלוסייה. הוא מבטיח איזון בין חקירה וניצול במרחב החיפוש כיוון ששיעור השחלוף יורד ככל שהאלגוריתם מתקרב לכשירות המרבית (`max_fitness`).
3. קריאת למתודת `crossover` לצורך שחלוף: בוררים זוגות של הורים, ומתודת השחלוף crossover מופעלת מה שמוביל ליצירת ילדים שיש להם שילובים של החומר הגנטי של ההורים ותורם לשמירת המגוון באוכלוסייה.
4. קריאה למתודה לצורך גרימת מוטציה: פרטים אקראיים באוכלוסייה נבחרים למוטציה. המתודה `mutate` מופעלת כדי להוסיף שונות לאוכלוסייה מה שתורם לאיתור פתרונות חדשים.
5. שילוב פרטים עיליים: פרטי העילית שנשמרו ללא שינוי מהדור הקודם (מסעיף 1) משולבים עם הצאצאים שעברו מוטציה ושחבור כדי ליצור את אוכלוסיית הדור החדש.

בסופה של כל ריצה של הלולאה, מוחזר הדור החדש של הפרטים. התהליך חוזר על עצמו עד להתכנסות או עד למספר ספציפי של דורות שמגדיר המשתמש.

השתמשתי בפרמטרים הבאים לצורך בחינת קוד הקלאס:

# Test case
weights = [7, 0, 30, 22, 80, 94, 11, 81, 70, 64, 59, 18, 0, 36, 3, 8, 15, 42, 9, 0,
  42, 47, 52, 32, 26, 48, 55, 6, 29, 84, 2, 4, 18, 56, 7, 29, 93, 44, 71,
  3, 86, 66, 31, 65, 0, 79, 20, 65, 52, 13]
values =  [360, 83, 59, 130, 431, 67, 230, 52, 93, 125, 670, 892, 600, 38, 48, 147,
 78, 256, 63, 17, 120, 164, 432, 35, 92, 110, 22, 42, 50, 323, 514, 28,
 87, 73, 78, 15, 26, 78, 210, 36, 85, 189, 274, 43, 33, 10, 19, 389, 276,
 312]
max_weight = 850
len_values = len(values)
gen_number = 1000 # # Number of generations to run if convergence is not achieved
population_size = 1000 # Constant number of solutions (individuals) in each generation
mutation_rate = 0.01 # Proportion of individuals to have a point mutation in each generation
elite_size = 0.05 # Proportion of the best individuals to pass without change  (a.k.a. mutation and crossover) to the next generation
convergence_threshold = 0.1  # Adjust the threshold based on your problem characteristics
convergence_generations = 5  # Number of generations with small improvement to trigger convergence
max_fitness = 10000  # Maximum fitness value to bound the dynamic crossover rate. The higher this parameter the higher the crossover rate in the initial stages.

genetic_solver = GeneticKnapsackSolver(weights, values, max_weight, gen_number, population_size, mutation_rate, elite_size, convergence_threshold, convergence_generations, max_fitness)

st = time.time()
genetic_solver.run()
et = time.time()
elapsed_time = et - st
print('Execution time genetic algorithm:', elapsed_time, 'seconds')

genetic_solver.summarize()

תוצאה שקיבלתי אחרי הפעם הראשונה בה הרצתי את האלגוריתם:

dynamic_crossover_rate = 0.2716358
generation: 352 * fitness: 7311 * selected_individual: [1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1]
Converged!
Execution time: 241.56041860580444 seconds
Top 5 Best Results:
1. Generation: 246, Fitness: 7405, Solution: [1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1]
2. Generation: 249, Fitness: 7405, Solution: [1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1]
3. Generation: 283, Fitness: 7405, Solution: [1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1]
4. Generation: 291, Fitness: 7405, Solution: [1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1]
5. Generation: 250, Fitness: 7380, Solution: [1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1]

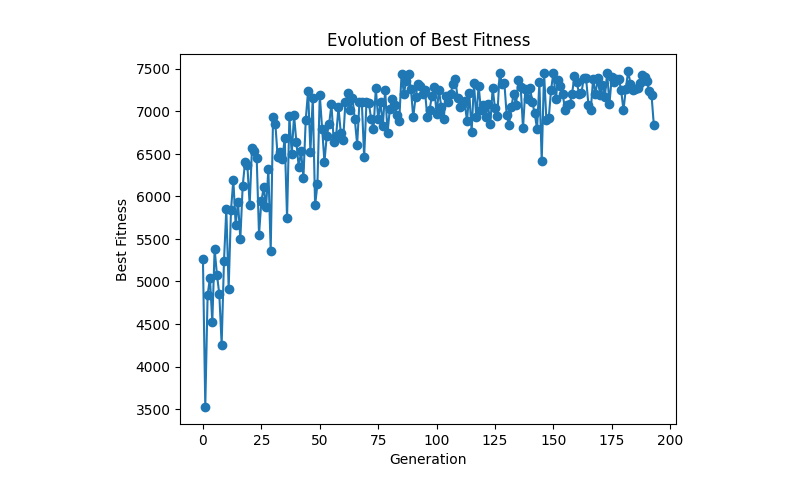
האלגוריתם הספיק לרוץ 351 דורות במשך 241 שניות לפני התכנסות כאשר שיעור ה-fitness הגבוה ביותר היה בדור 246 שם הכשירות היתה 7405. אפשר לראות את המבנה הגנטי (=אילו פריטים הוכנסו לתרמיל) שהוביל לתוצאה.

• האלגוריתם אינו דטרמיניסטי ועל כן בכל הרצה תתקבל תוצאה שונה.

הקוד המלא:

לחץ להורדת קובץ קלאס פייתון אלגוריתם גנטי שאותו נפתח במדריך

import math
import random
import time
import pprint

import matplotlib.pyplot as plt

pp = pprint.PrettyPrinter(width=41, compact=True)

class GeneticKnapsackSolver:
    def __init__(self, weights, values, max_weight, gen_number, population_size, mutation_rate, elite_size, convergence_threshold, convergence_generations, max_fitness):
        self.weights = weights
        self.values = values
        self.len_values = len(values)
        self.max_weight = max_weight
        self.gen_number = gen_number
        self.population_size = population_size
        self.mutation_rate = mutation_rate
        self.elite_size = elite_size
        self.convergence_threshold = convergence_threshold
        self.convergence_generations = convergence_generations
        self.best_results = []
        self.improvements = []
        self.max_fitness = max_fitness

    def fitness(self, solution):
        # Calculate the total weight of the solution using element-wise multiplication.
        solution_weight = sum(x * y for x, y in zip(solution, self.weights))

        # Calculate the total value of the solution using element-wise multiplication.
        calculated_fitness = sum(x * y for x, y in zip(solution, self.values))

        # Check if the total weight exceeds the maximum allowable weight.
        if solution_weight > self.max_weight:
            # If the weight limit is exceeded, assign a fitness score of -1 to indicate infeasibility.
            calculated_fitness = -1

        # Return the calculated total value as the fitness score for the feasible solution.
        return calculated_fitness

    def make_individual(self):
        # Generate a list of 1s and 0s representing a potential solution.
        # Each list item corresponds to a decision variable for the knapsack problem.
        # 1 indicates inclusion, 0 indicates exclusion.
        individual = [random.randint(0, 1) for _ in range(self.len_values)]

        return individual

    def make_population(self):
        # Generate a list of individuals, each representing a potential solution to the problem.
        # The population is a collection of these individuals.
        population = [self.make_individual() for _ in range(self.population_size)]

        return population

    def rank_individuals(self, population):
        # Rank the individuals that make the population by how fit they are.
        ranked_individuals = [(self.fitness(individual), individual) for individual in population]
        ranked_individuals.sort(reverse=True)

        return ranked_individuals

    def fitness_proportionate_selection(self, population):
        # Biased roulette wheel selection -
        # individuals with higher fitness have higher probabilities of being selected for the next generation

        # Extract fitness scores from the population
        fitness_scores = [fitness_score for fitness_score, _ in population]

        # Calculate the total fitness of the population
        total_fitness = sum(fitness_scores)

        # Calculate probabilities for each individual based on their fitness
        probabilities = [fitness / total_fitness for fitness in fitness_scores]

        # Select individuals using a biased roulette wheel with calculated probabilities
        selected_indices = random.choices(range(len(population)), weights=probabilities, k=len(population))

        # Retrieve the selected individuals based on their indices
        selected_individuals = [population[i] for i in selected_indices]

        return probabilities, selected_individuals

    def get_parent(self, population):
        # Get probabilities and selected individuals.
        probabilities, selected_individuals = self.fitness_proportionate_selection(population)

        # Generate a random number between 0 and 1.
        rand_num = random.uniform(0, 1)

        # Initialize a variable to track the cumulative probability.
        total = 0

        # Iterate over the probabilities to find the selected individual.
        for i in range(len(probabilities)):
            # Add the current probability to the cumulative total
            total += probabilities[i]
            # Check if the cumulative total exceeds the random number
            if total > rand_num:
                # Return the selected individual
                return selected_individuals[i]

        # If the loop completes and no individual is selected, return the last one
        return selected_individuals[i - 1]

    def crossover(self, parent1, parent2):
        # Select a random index to perform the crossover.
        rand_idx = random.randint(0, self.len_values - 1)

        # Create the first child by combining the first half of parent1 with the second half of parent2.
        child1 = parent1[:rand_idx] + parent2[rand_idx:]

        # Create the second child by combining the first half of parent2 with the second half of parent1.
        child2 = parent2[:rand_idx] + parent1[rand_idx:]

        # Return the recombined children resulting from the crossover operation.
        return child1, child2

    def mutate(self, individual):
        # Select a random index for point mutation.
        rand_idx = random.randint(0, self.len_values - 1)

        # Switch 0 to 1 or 1 to 0 at the selected index to introduce mutation.
        mutated_val = 1 if individual[rand_idx] == 0 else 0
        individual[rand_idx] = mutated_val

        # Return the mutated individual.
        return individual

    def pick_mutated_indices(self):
        # List to store the randomly selected indices for mutation.
        mutated_indices = []

        # Calculate the number of mutations based on the mutation rate.
        mutations_number = math.ceil(self.population_size // (1 / self.mutation_rate))

        # Pick individuals for mutation iteratively.
        for _ in range(mutations_number):
            # Select a random index for mutation based on the mutation rate.
            mutated_idx = random.randint(0, 1 / self.mutation_rate)

            # Check if the index is within the bounds of the population.
            if mutated_idx < self.population_size - 1:
                mutated_indices.append(mutated_idx)

        # Return the list of randomly selected indices for mutation.
        return mutated_indices

    def make_generation(self, prev_gen):
        # List to store individuals for the new generation.
        population = []

        # Select a fixed percentage of the best individuals as elite
        elite_size = int(self.elite_size * self.population_size)
        elite_individuals = [ind[1] for ind in prev_gen[:elite_size]]

        # Calculate dynamic crossover rate based on the average fitness of the population.
        avg_fitness = sum(ind[0] for ind in prev_gen) / len(prev_gen)

        # Ensure the crossover rate (dynamic_crossover_rate) stays within a reasonable range of 0.2 to 1.0.
        # The value of `dynamic_crossover_rate` decreases as the algorithm approaches the maximum fitness (`max_fitness`).
        dynamic_crossover_rate = max(0.2, min(1.0, 1.0 - (avg_fitness / max_fitness)))
        print(f"dynamic_crossover_rate = {dynamic_crossover_rate}")

        # Perform crossovers to create children from pairs of parents.
        for _ in range((self.population_size - elite_size) // 2):
            # Select two parents from the previous generation.
            parent1 = self.get_parent(prev_gen)
            parent2 = self.get_parent(prev_gen)

            # Apply crossover with the dynamic crossover rate.
            if random.uniform(0, 1) < dynamic_crossover_rate:
                # Create two children by recombining the genetic material of the parents.
                child1, child2 = self.crossover(parent1[1], parent2[1])
            else:
                child1, child2 = parent1[1], parent2[1]

            # Add the children to the current generation's population.
            population.extend([child1, child2])

        # Mutate random individuals in the population.
        mutated_indices = self.pick_mutated_indices()
        for idx in mutated_indices:
            population[idx] = self.mutate(population[idx])

        # Combine elite individuals with the offspring
        population.extend(elite_individuals)

        # Return the new generation of individuals.
        return population

    def summarize(self):
        sorted_best_results = sorted(self.best_results, key=lambda x: x[1], reverse=True)

        print("Top 5 Best Results:")
        for i in range(min(5, len(sorted_best_results))):
            print(f"{i + 1}. Generation: {sorted_best_results[i][0]}, Fitness: {sorted_best_results[i][1]}, Solution: {sorted_best_results[i][2]}")

        # Visualize
        fitness_values = [result[1] for result in self.best_results]

        plt.plot(range(len(fitness_values)), fitness_values, marker='o')
        plt.xlabel('Generation')
        plt.ylabel('Best Fitness')
        plt.title('Evolution of Best Fitness')
        plt.show()

    def run(self):
        # Initialize the first generation
        population = self.make_population()
        # Rank solutions and choose the best for the next generation
        ranked_individuals = self.rank_individuals(population)
        _, selected_individuals = self.fitness_proportionate_selection(ranked_individuals)
        
        # Run the specified number of generations
        for gen_number in range(self.gen_number):
            # Generate the new generations based on the previous generation
            population = self.make_generation(selected_individuals)
            # Rank new solutions and choose the best for the subsequent generation
            ranked_individuals = self.rank_individuals(population)
            _, selected_individuals = self.fitness_proportionate_selection(ranked_individuals)
            
            # Record current generation results and track improvement
            selected_individual = selected_individuals[0]
            current_highest_fitness = selected_individual[0]
            current_highest_genetic_makeup = selected_individual[1]
            print(f"generation: {gen_number} * fitness: {current_highest_fitness} * selected_individual: {current_highest_genetic_makeup}")


            self.best_results.append((gen_number, current_highest_fitness, current_highest_genetic_makeup))

            if gen_number > 1:
                # Calculate improvement from the last generation.
                improvement = current_highest_fitness - self.best_results[-2][1]
                self.improvements.append(improvement)

            # Converge based on improvement criteria
            if gen_number >= self.convergence_generations and all(imp < self.convergence_threshold for imp in
                                                                  self.improvements[-self.convergence_generations:]):
                print("Converged!")
                break

# Test case
weights = [7, 0, 30, 22, 80, 94, 11, 81, 70, 64, 59, 18, 0, 36, 3, 8, 15, 42, 9, 0,
   42, 47, 52, 32, 26, 48, 55, 6, 29, 84, 2, 4, 18, 56, 7, 29, 93, 44, 71,
   3, 86, 66, 31, 65, 0, 79, 20, 65, 52, 13]
values =  [360, 83, 59, 130, 431, 67, 230, 52, 93, 125, 670, 892, 600, 38, 48, 147,
  78, 256, 63, 17, 120, 164, 432, 35, 92, 110, 22, 42, 50, 323, 514, 28,
  87, 73, 78, 15, 26, 78, 210, 36, 85, 189, 274, 43, 33, 10, 19, 389, 276,
  312]
max_weight = 850
len_values = len(values)
gen_number = 1000 # # Number of generations to run if convergence is not achieved
population_size = 1000 # Constant number of solutions (individuals) in each generation
mutation_rate = 0.01 # Proportion of individuals to have a point mutation in each generation
elite_size = 0.05 # Proportion of the best individuals to pass without change  (a.k.a. mutation and crossover) to the next generation
convergence_threshold = 0.1  # Adjust the threshold based on your problem characteristics
convergence_generations = 5  # Number of generations with small improvement to trigger convergence
max_fitness = 10000  # Maximum fitness value to bound the dynamic crossover rate. The higher this parameter the higher the crossover rate in the initial stages.

genetic_solver = GeneticKnapsackSolver(weights, values, max_weight, gen_number, population_size, mutation_rate, elite_size, convergence_threshold, convergence_generations, max_fitness)

st = time.time()
genetic_solver.run()
et = time.time()
elapsed_time = et - st
print('Execution time:', elapsed_time, 'seconds')

genetic_solver.summarize()

סיכום

במדריך זה, יצרנו קלאס Python המיישם אלגוריתם גנטי כדי לפתור את בעיית התרמיל – בעיה הדורשת מקסום של ערך תוך מזעור משקל האחסון. בחרנו באלגוריתם גנטי לעומת שיטות אנליטיות בשל יעילותו במציאת פתרונות או קירובים עבור בעיות מאתגרות במיוחד, לרבות אלו הנכללות תחת מחלקת ה-NP. אלגוריתמים גנטיים משתייכים לתחום האלגוריתמים האבולוציוניים, אשר מחקים תהליכים טבעיים כדי להתמודד עם אתגרי תכנות. הם מצטיינים במיוחד בפתרון בעיות אופטימיזציה, כפי שהראנו בפתרון בעיית התרמיל. יישומים נוספים כוללים פיתוח של רובוטים לומדים בעצמם, יצירת מודלים פיננסיים מתקדמים, עיבוד אותות, הענקת התנהגויות אינטליגנטיות למשחקי מחשב ועוד.

מדריכים נוספים שעשויים לעניין אותך בסדרה על למידת מכונה

אופטימיזציה עבור למידה בצוותא ensemble learning

חיזוי מחירי מכוניות - XGBoost, Optuna, SHAP, ועוד הרבה דברים טובים...

מודל למידת מכונה - XGBoost - לראות את העצים בתוך היער

הטרנספורמרים משנים את עולם הבינה המלאכותית

לכל המדריכים בנושא של למידת מכונה

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים