התפלגות גיאומטרית ישר ולעניין עם קוד פייתון

משה מהפועל "ארגזים" עולה מהספסל וידוע שהוא מבקיע בממוצע 25% מהפנדלים שהוא בועט. מה הסיכוי שלו להבקיע בפעם הראשונה בניסיון השלישי? זו דוגמה לבעיה שאפשר לענות עליה בעזרת התפלגות גיאומטרית.

ההתפלגות הגיאומטרית עוסקת בספירת הניסיונות הדרושים כדי להגיע להצלחה הראשונה בסדרה של ניסויים עצמאיים.

לדוגמה, הטלת מטבע שוב ושוב עד שמקבלים "ראש". כל הטלת מטבע היא ניסוי. התוצאות האפשריות הם: "ראש" או "זנב". התוצאה הרצויה היא "ראש". אחרי שמקבלים בפעם הראשונה "ראש" מפסיקים את סדרת הניסויים.

דוגמאות לשימוש בהתפלגות גאומטרית הם:

• הטלת מטבע עד הפעם הראשונה שבה הוא נוחת על "ראש".
• זריקת קוביה עד שהיא מראה בפעם הראשונה מספר מסויים (לדוגמה, 4).
• בחינה סדרתית של רכיבים אלקטרוניים עד שמוצאים את הראשון שאינו תקין.

המשותף לכל הדוגמאות הוא שחוזרים על ניסוי שיש לו שתי תוצאות אפשריות עד שהתוצאה הרצויה מופיעה בפעם הראשונה.

שתי תוצאות אפשריות זה אומר "הצלחה" או "כישלון" כאשר התוצאה הרצויה היא מה שמעניין אותנו, ואותה נגדיר "הצלחה". אנחנו יכולים להחליט שהצלחה מבחינתנו היא קבלת "ראש" בהטלת מטבע, 4 נקודות בהטלת קוביה, או רכיב אלקטרוני שאינו תקין. למרות שהרכיב אינו תקין את תוצאת הניסוי "לא תקין" אנחנו מגדירים כ"הצלחה" כי זו התכונה מבין השתיים ("תקין" לעומת "לא תקין") בה אנו מעוניינים.

כדי להשתמש בהתפלגות גאומטרית הנתונים הנבדקים צריכים שיהיו להם את 3 התכונות הבאות:

1. עצמאות: כל ניסוי אינו תלוי באחרים. התוצאה של ניסוי אחד לא משפיעה על התוצאה של אחר.
2. שתי תוצאות: לכל ניסוי יש רק שתי תוצאות אפשריות, "הצלחה" או "כישלון".
3. ההסתברות להצלחה (p) נשארת קבועה בכל הניסויים.

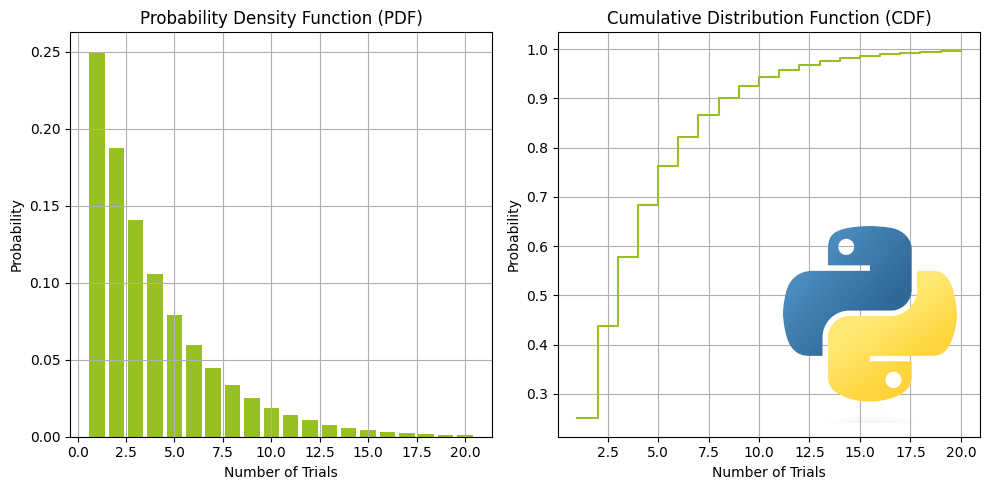
פונקציית הצפיפות PDF של ההתפלגות הגיאומטרית

את ההתפלגות הגיאומטרית ניתן להגדיר באופן יותר מדויק כמתארת את ההסתברות להשגת ההצלחה הראשונה בעקבות רצף של כשלונות רצופים, כאשר ניתן לעשות מספר בלתי מוגבל של ניסיונות עד להצלחה.

נוסחת ההתפלגות הגיאומטרית היא:

$$ P(X = k) = (1 - p)^{k-1} * p $$

כאשר:

• P(X=k) היא ההסתברות להצלחה ראשונה בניסוי שמספרו k
• p היא ההסתברות להצלחה בכל ניסוי
• (1-p) הוא המשלים או הסיכוי לכישלון בכל ניסוי
• k הוא מספר הניסויים עד להצלחה הראשונה

במילים, כדי לחשב את ההסתברות להצלחה בניסוי שמספרו k בסדרת ניסויים כאשר הסיכוי להצלחה בכל ניסוי הוא p צריך להעלות בחזקה (k-1) את הסיכוי לכישלון (1-p) ואז לכפול בסיכוי להצלחה שהוא p.

למה לכפול בין תוצאות הניסויים? מייד נסביר אבל קודם נענה על שאלה.

משה מהפועל "ארגזים" עולה מהספסל וידוע שהוא מבקיע בממוצע 25% מהפנדלים שהוא בועט. מה הסיכוי שלו להבקיע בפעם הראשונה בניסיון השלישי?

את המשתנים הנתונים בשאלה:

$$ k = 3 \\ p = 0.25 $$

נציב בנוסחת ההתפלגות הגיאומטרית, ונקבל הסתברות של 14.06% שמשה יבקיע לראשונה כשהוא בועט לשער בפעם השלישית:

$$ P(X = 3) = (1 - 0.25)^{3-1} * 0.25 = 14.06 \% $$

ההסבר לנוסחה הוא שאם הניסויים אינם תלויים אז כדי לקבל את הסיכוי להתרחשותם המשותפת צריך להכפיל את הסיכוי לכל תוצאה. במקרה שלנו, הסיכוי לשני כשלונות הינו 1-0.25=0.75 בחזקת 2, והסיכוי להצלחה בניסוי השלישי הוא 0.25

גרף פונקציית הצפיפות pdf של ההתפלגות הגיאומטרית מציג את ההסתברויות לערכים שונים של k. לדוגמה, גרף המציג את ההתפלגות של הבקעת פנדל (בהנחה ששיעור ההצלחה p=0.25).

נעזר בפייתון לצורך הצגת גרף פונקציית הצפיפות של ההסתברות הגיאומטרית עם סיכויי הצלחה 0.25:

import numpy as np
import matplotlib.pyplot as plt


# Probability of success
p = 0.25


# Define the range of number of rolls
x = np.arange(1, 21)  # Let's consider up to 20 rolls


# Calculate the PDF (Probability Density Function)
pdf = (1 - p) ** (x - 1) * p


# Plot PDF
plt.figure(figsize=(10, 5))
plt.bar(x, pdf, color='#97c022')
plt.title('Probability Density Function (PDF)')
plt.xlabel('Number of Trials')
plt.ylabel('Probability')


plt.tight_layout()
plt.show()

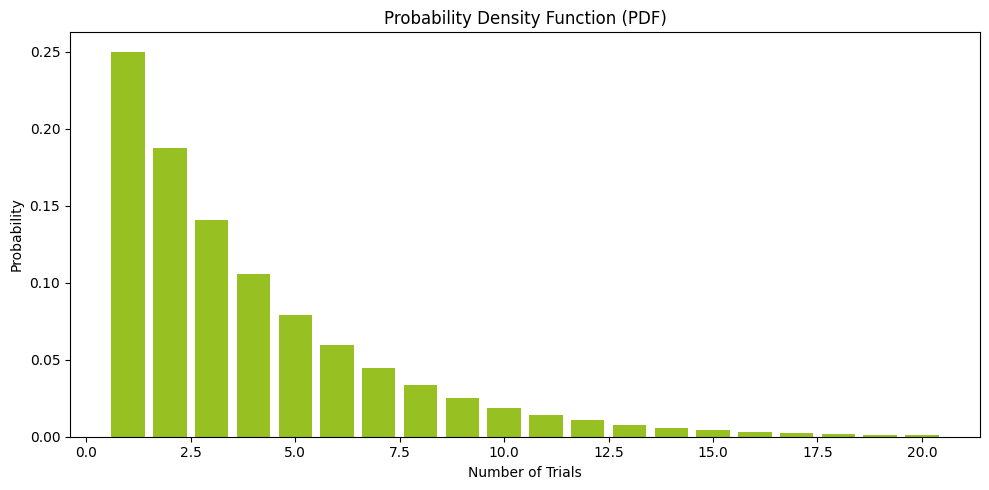
• ציר ה-x הוא הפעם הראשונה שבה מצליחים (k בנוסחה)
• ציר ה-y הוא ההסתברות להצלחה עבור ערך מסוים של x.
• הערך הגבוה ביותר הוא 0.25 (שיעור ההצלחה)
• ככל ש-x גדל ההסתברות להצלחה פוחתת.
• הגרף מציג חלק מהתוצאות כי ההסתברות יכולה להגיע עד אינסוף ערכים של x.

פונקציית ההסתברות המצטברת CDF של ההתפלגות הגיאומטרית

נוסף לפונקציית הצפיפות PDF חשוב להכיר את פונקציית ההסתברות המצטברת (CDF = Cumulative Distribution Function) עבור ההתפלגות הגיאומטרית.

אם המשחק מסתיים אחרי הבקעת פנדל אחד אז מה שמעניין אותנו הוא לא רק מה הסיכוי להבקעה בפעם השלישית אלא גם מה הסיכוי להבקיע בפעם השלישית או קודם לכך. לצורך זה, אנחנו יכולים לחבר את כל ההסתברויות מ-1 עד 3. זה אומר לנו מה הסיכוי לקבל הצלחה ב-3 או פחות ניסיונות.

נוסחת ההסתברות המצטברת (CDF) מחשבת כמה זמן אנחנו צריכים לחכות לתוצאה מסוימת תוך שאנחנו לוקחים בחשבון שניתן לקבל הצלחה בניסוי שמספרו k או עוד לפני כך.

נוסחת ה-CDF עבור ההתפלגות הגיאומטרית היא:

$$ F(x) = 1 - (1 - p)^k $$

כדי לחשב את ההסתברות של משה להבקיע פנדל ב-3 בעיטות או פחות נציב את המשתנים בנוסחת ה-CDF:

$$ k = 3 \\ p = 0.25 $$

$$ F(x) = 1 - (1 - 0.25)^3 = 57.8\% $$

• במילים: ההסתברות של משה להבקיע ב-3 בעיטות או פחות לשער היא 57.8%

נשתמש בפייתון לתיאור גרף ההסתברות המצטברת CDF עבור סיכויי הצלחה של p=0.25:

# Probability of success
p = 0.25

# Define the range of number of rolls
x = np.arange(1, 21)  # Let's consider up to 20 rolls

# Calculate the PDF (Probability Density Function)
pdf = (1 - p) ** (x - 1) * p

# Plot PDF
plt.figure(figsize=(10, 5))
plt.bar(x, pdf, color='#97c022')
plt.title('Probability Density Function (PDF)')
plt.xlabel('Number of Trials')
plt.ylabel('Probability')

plt.tight_layout()
plt.show()

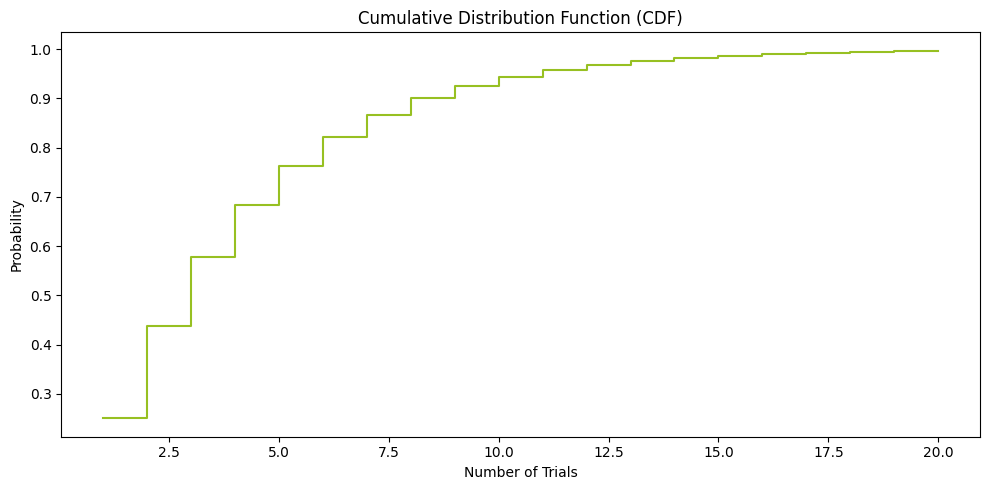
• ככל שמתקדמים משמאל לימין על ציר ה-x כך הערך המצטבר בציר ה-y מתקרב ל-1. כבר בניסיון ה-15 ההסתברות המצטברת היא ממש קרובה ל- 1, ומעבר לזה כבר אי אפשר (כי הסתברות תחומה בין 0 ל-1).

תכונות נוספות של ההתפלגות הגיאומטרית

ממוצע ההתפלגות הגיאומטרית הוא:

$$ Mean = 1/p $$

• מה שאומר שכדי לקבל את מספר הפנדלים הממוצע שמשה צריך לבעוט לשער כדי להצליח להבקיע פנדל ראשון הוא 1 חלקי 0.25 שזה יוצא 4 פנדלים. זה הגיוני כי ככל שהסיכוי להצלחה בניסוי בודד היא קטנה יותר נצטרך לנסות יותר כדי להצליח. לדוגמה, אם הסיכוי להצלחה הוא עשירית אז נצטרך בממוצע 10 בעיטות לשער כדי להצליח להבקיע את הפנדל הראשון.

השונות היא :

$$ Mean = 1/p^2 $$

הערך השכיח הוא p ההסתברות להצלחה.

$$ Mode = p $$

התפלגות גיאומטרית והקשר שלה להתפלגות בינומית

התפלגות גיאומטרית דומה ל התפלגות בינומית. בעוד ההתפלגות הגיאומטרית מחשבת את ההסתברות להצלחה בניסוי שמספרו n, ההתפלגות הבינומית מחשבת את הסיכוי למספר n של הצלחות במספר ידוע מראש של ניסויים.

מדריכים נוספים בסדרה על למידת מכונה שעשויים לעניין אותך

מדריך הסתברות מעריכית (אקספוננציאלית) מהלכה למעשה עם פייתון

מדריך מעשי על התפלגות פואסנית באמצעות קוד פייתון וציפורים נודדות

התפלגות בינומית - הלכה למעשה

לכל המדריכים בנושא של למידת מכונה

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים