שימוש בדגימת תומפסון להתמודדות עם דילמת השודד בעל הזרועות המרובות

דמיין שאתה מנהל של אתר אינטרנט, ויש לך אפשרות להציג רק מודעה אחת בכל פעם בדף הבית, ולשם כך אתה צריך לבחור בין מספר מודעות פוטנציאליות. כל מודעה מניבה רווח שאינו ידוע מראש. המטרה היא למקסם את ההכנסות על ידי בחירת המודעה המשתלמת ביותר, אף שאינך יודע איזו מביניהם הינה המוצלחת ביותר.

אתה מעוניין להגדיל את הרווח שלך כמה שניתן, ולשם כך אתה צריך לאזן בין שתי אפשרויות:

• חקר (Exploration) - ניסוי של מודעות כמה שיותר פעמים לפני שמתחייבים על האחת הרווחית ביותר.
• ניצול (Exploitation) - שימוש במודעה שנראה שמניבה את הפרס הגבוה ביותר בהתבסס על הנתונים הקיימים.

דילמת השודד בעל הזרועות המרובות Multi-Armed Bandit מנסחת את האתגר הזה באופן פורמלי, ודגימת תומפסון Thompson Sampling מהווה פתרון אלגנטי לבעיה.

דילמת השודד בעל הזרועות המרובות ה-Multi-Armed Bandit

דילמת ה- Multi-Armed Bandit הינה בעיה בה סוכן נדרש לבחור בין מספר חלופות (או "זרועות") כדי למקסם את הסך הכולל של הפרסים לאורך זמן. האלגוריתם מאזן בין חקר (Exploration) – איסוף מידע על כל אפשרות, לבין ניצול (Exploitation) – שימוש באפשרות אשר מניבה את התוצאה הגבוהה ביותר בהתבסס על הנתונים הקיימים.

המונח " השודד בעל הזרועות המרובות" נובע ממטאפורה של מהמר העומד מול שורה של מכונות מזל – המכונות הללו נקראות לעיתים "שודדים בעלי זרוע אחת" עקב הידית היחידה שבכל אחת מהן. בתרחיש זה, המהמר צריך להחליט באיזו מכונה לשחק, לקבוע כמה פעמים לשחק בכל אחת, ולבחור את הסדר שבו ינסה את המכונות. האתגר הוא לאזן בין הישארות עם מכונה אשר מניבה את הרווחים הגבוהים ביותר לבין ניסוי של מכונות אחרות אשר עשויות, בתרחיש האופטימי, להניב תשואות גבוהות עוד יותר.

יסודות בייסיאניים של דגימת תומפסון Thompson Sampling

העיקרון הבסיסי מאחורי אלגוריתם Thompson Sampling הוא עדכון של אמונות באמצעות שיטת בייס Bayes:

• מתחילים מהנחות מקדימות (Prior) אשר משקפות את חוסר הוודאות לגבי ממוצע הרווח מכל זרוע. כשלא יודעים למה לצפות, בחירה מקובלת היא הנחה מקדימה שטוחה - התפלגות (נורמלית) עם שונות גדולה.
• לאחרת שמושכים בידיות, מקבלים התפלגות מאוחרת (Posterior) ואז באמצעות שיטת בייס, מעדכנים את האמונה לגבי ממוצע הפרס לכל זרוע על סמך התצפיות.

לדוגמה, אם מניחים שההתפלגות הסבירה הראשונית היא נורמלית עם שונות ידועה:

$$ \mu_{0},\,\sigma_{0}^{2} $$

הפרמטרים של ההתפלגות הפוסטיריורית הם:

$$ {\frac {1}{{\frac {1}{\sigma _{0}^{2}}}+{\frac {n}{\sigma ^{2}}}}}\left({\frac {\mu _{0}}{\sigma _{0}^{2}}}+{\frac {\sum _{i=1}^{n}x_{i}}{\sigma ^{2}}}\right),\left({\frac {1}{\sigma _{0}^{2}}}+{\frac {n}{\sigma ^{2}}}\right)^{-1} $$

ככל שצוברים יותר נתונים, ההתפלגות הפוסטיריורית מתרכזת יותר הודות לצמצום השונות, וההערכה של הממוצע מתקרבת לערך האמיתי.

האלגוריתם של דגימת תומפסון Thompson Sampling

אלגוריתם Thompson Sampling פועל באופן איטרטיבי כדלקמן:

1. אתחול: עבור כל זרוע, בוחרים התפלגות מקדימה משוערת עבור ממוצע הפרס שלה.

2. דגימה: עבור כל זרוע דוגמים ערך מההתפלגות המאוחרת (הפוסטיריורית) אשר נחשפה במדגם.

3. בחירה: בוחרים את הזרוע בעלת ערך המדגם הגבוה ביותר.

4. תצפית ועדכון: מפעילים את הזרוע הנבחרת (למשל, מציגים את המודעה), מקבלים את הפרס, ומעדכנים את ההתפלגות המאוחרת של הזרוע באמצעות נוסחאות העדכון.

5. חזרה: ממשיכים בתהליך עם כל תצפית חדשה, תוך עדכון מתמיד של האמונות לגבי כל זרוע.

תהליך זה עשוי להבטיח שגם אם זרוע עם פרס גבוה נבחרת לעיתים קרובות, עדיין קיימת אפשרות לחקור זרועות אחרות במידה וחוסר הוודאות לגביהן גבוה מספיק.

דוגמה שלב-אחרי-שלב: דגימת תומפסון בפעולה

מתחילים ממצב של אי-ודאות

נניח שיש לך שלוש מודעות (A, B, ו-C). עבורם נגדיר את הפרמטרים הבאים.

• לכל מודעה נבחר "הנחה מקדימה שטוחה" אשר מבטאת חוסר ודאות גבוהה:

$$ \mu_0 = 0 $$

$$ \sigma_0^2 = 100 $$

• ההתפלגות מבוססת בשלב הראשון על הנחה של ממוצע 0 ושונות גבוהה 100.

• הנחה מקדימה שטוחה היא רעיון טוב כשאינך יודע מראש מה צפוי להיות הרווח מכל זרוע. אם יש לך ידע מקדים זה המקום להשתמש בו אחרת תהליך העדכון הבייסיאני עלול, בפרט באיטרציות הראשונות, לנטות לכיוון הזרועות אשר מניבות תשואה פחותה.

איטרציה 1:

• דגימה: עבור כל פרסומת (A, B ו-C), האלגוריתם שולף ערך אקראי מהתפלגות ההסתברות שלה. ערך זה מייצג רווח אפשרי עבור אותה פרסומת.

• בחירה: נניח שערך המדגם (האקראי) של מודעה B הוא הגבוה ביותר.

• תצפית: מציגים את המודעה הנבחרת ועוקבים אחר הרווח שהניבה.

• עדכון: בסיום שלב התצפית, מעדכנים את ההתפלגות המאוחרת עבור מודעה B עם הרווח בפועל, דבר המצמצם את אי הוודאות לגביה.

איטרציה 2:

• דגימה: דוגמים מההתפלגות עבור כל מודעה, תוך שימוש בהתפלגות המעודכנת עבור מודעה B , ובהנחות המקדימות, שטרם עודכנו, עבור מודעות A ו-C

• בחירה ועדכון: האלגוריתם בוחר את הפרסומת עם הערך הדגימה הגבוה ביותר, מציג אותה ומעדכן את התפלגות ההסתברות המתאימה בהתבסס על התוצאה בפועל.

ביתר האיטרציות

עם התקדמות האיטרציות, מצטברים יותר נתונים, ואז:

• התפלגויות ההסתברות משתנות ומצטמצמות: הערכות הרווח עבור כל מודעה נעשות מדויקות יותר, וחוסר הוודאות קטן בהתאם.

• איזון בין חקר לניצול: המערכת נוטה לבחור את המודעה שמציגה באופן עקבי ביצועים טובים (ניצול), אך עדיין מדי פעם בוחרת מודעות אחרות כדי לבדוק אם ייתכן והן מציעות ביצועים משופרים (חקר).

• בחירה מושכלת: בסופו של דבר, המערכת "לומדת" איזו מודעה היא האופטימלית, אך עדיין ממשיכה לבדוק, מדי פעם, אפשרויות נוספות כדי להישאר מעודכנת במידה והמצב משתנה.

מימוש Thompson sampling באמצעות קוד Python

להלן קוד Python פשוט המדגים הגדרה של בעיית בנדיט רב-זרועי ושימוש ב-Thompson Sampling תוך הנחת נורמליות.

את ההתפלגויות הקוד מייצר בתוך קלאס GaussianBandit, כאשר הקלאס ThompsonSampling אחראי על תהליך הדגימה עצמו:

import numpy as np
    import matplotlib.pyplot as plt
    from scipy.stats import norm
    
    
    class GaussianBandit:
       def __init__(self, true_mean, true_std):
           self.true_mean = true_mean
           self.true_std = true_std
    
    
       def pull(self):
           return np.random.normal(self.true_mean, self.true_std)
    
    
    class ThompsonSampling:
       def __init__(self, n_arms, prior_mean=0, prior_std=100, likelihood_std=10):
           self.n_arms = n_arms
           self.likelihood_var = likelihood_std**2
           # Initialize prior parameters for each arm
           self.prior_mean = np.full(n_arms, prior_mean)
           self.prior_var = np.full(n_arms, prior_std**2)
           # Initialize counters and cumulative rewards
           self.n_pulls = np.zeros(n_arms)
           self.sum_rewards = np.zeros(n_arms)
    
    
       def sample(self):
           samples = np.zeros(self.n_arms)
           for i in range(self.n_arms):
               n = self.n_pulls[i]
               prior_var = self.prior_var[i]
               if n == 0:
                   # No data yet: use the prior
                   post_var = prior_var
                   post_mean = self.prior_mean[i]
               else:
                   post_var = 1 / (1/prior_var + n/self.likelihood_var)
                   post_mean = post_var * (self.prior_mean[i]/prior_var + self.sum_rewards[i]/self.likelihood_var)
               samples[i] = np.random.normal(post_mean, np.sqrt(post_var))
           return samples
    
    
       def update(self, arm, reward):
           self.n_pulls[arm] += 1
           self.sum_rewards[arm] += reward

בנוסף, הקוד כולל פונקציה האחראית על הצגת הגרפים המתארים את התפלגות הרווח עבור המודעות השונות תוך כדי תהליך הדגימה:

def plot_normal_posteriors(thompson, iteration):
       """
       Plots the posterior normal distributions for each arm.
       The title indicates the current iteration.
       """
       n_arms = thompson.n_arms
       params = []
       for i in range(n_arms):
           n = thompson.n_pulls[i]
           prior_var = thompson.prior_var[i]
           prior_mean = thompson.prior_mean[i]
           if n == 0:
               post_mean = prior_mean
               post_var = prior_var
           else:
               post_var = 1 / (1/prior_var + n/thompson.likelihood_var)
               post_mean = post_var * (prior_mean/prior_var + thompson.sum_rewards[i]/thompson.likelihood_var)
           post_std = np.sqrt(post_var)
           params.append((post_mean, post_std))
    
    
       # Create a common x-range that covers all distributions
       xs = []
       for post_mean, post_std in params:
           xs.extend(np.linspace(post_mean - 4*post_std, post_mean + 4*post_std, 100))
       xs = np.array(xs)
       x_min, x_max = xs.min(), xs.max()
       x = np.linspace(x_min, x_max, 1000)
    
    
       plt.figure(figsize=(10, 6))
       # Generate as many colors as needed using a colormap
       colors = plt.cm.jet(np.linspace(0, 1, n_arms))
       for i in range(n_arms):
           post_mean, post_std = params[i]
           y = norm.pdf(x, post_mean, post_std)
           plt.plot(x, y, color=colors[i], linewidth=2,
                    label=f'Arm {i+1}: μ={post_mean:.2f}, σ={post_std:.2f}')
    
    
       plt.xlabel('Reward')
       plt.ylabel('Probability Density')
       plt.title(f'Posterior Distributions for Each Arm at Iteration {iteration}')
       plt.legend()
       plt.grid(True)
       plt.show(block=False)
       plt.pause(1)   # Pause for 1 second; adjust as needed
       plt.close()

בחלקו הבא של הקוד נשתמש בקלאסים שכבר פיתחנו לצורך ביצוע דגימת תומפסון הלכה למעשה:

• הדגימה היא מ-10 מודעות (או זרועות) בעלות ממוצעי רווח אמיתיים הנעים בין 40 ל-49 כאשר כל מודעה מניבה רווח הגבוה ב-1 מקודמתה. העובדה שממוצעי הרווח קרובים כל כך, לצד ערך שונות גבוה של 10, נועדת להקשות על האלגוריתם לזהות את המודעה הטובה ביותר.

האלגוריתם של Thompson Sampling משמש לבחירת המודעה המניבה את הרווח הגבוה ביותר בכל איטרציה כשבמקרה שלנו הוא ירוץ 1000 פעמים כדי לאפשר לו מספיק ניסיונות להתמודד עם המשימה הקשה בה הוא צריך לעמוד.

# Example usage:
    np.random.seed(67)
    
    
    # Define true means for an arbitrary number of bandits, e.g., 10 bandits:
    true_means = [40, 41, 42, 43, 44, 45, 46, 47, 48, 49]
    likelihood_std = 10  # Standard deviation for the GaussianBandit
    n_iterations = 1000
    
    
    bandits = [GaussianBandit(true_mean, true_std=likelihood_std) for true_mean in true_means]
    
    
    # Use the number of bandits as the number of arms
    n_arms = len(bandits)
    thompson = ThompsonSampling(n_arms, likelihood_std=likelihood_std)
    
    
    rewards = np.zeros(n_iterations)
    choices = np.zeros(n_iterations)
    
    
    # Define snapshot iterations: 0, 1, 2, 10, and every 100th iteration.
    snapshot_iters = set([0, 1, 2, 10])
    for t in range(n_iterations):
       if (t+1) % 100 == 0:
           snapshot_iters.add(t+1)
    snapshot_iters = sorted(list(snapshot_iters))
    
    
    # Plot initial state (iteration 0)
    if 0 in snapshot_iters:
       plot_normal_posteriors(thompson, 0)
    
    
    for t in range(n_iterations):
       # Get a sample from each posterior
       samples = thompson.sample()
    
    
       # Choose the arm which yields the highest revenue
       chosen_arm = np.argmax(samples)
    
    
       # Get a new reward from the chosen arm
       reward = bandits[chosen_arm].pull()
    
    
       # Update the specific arm's distribution posterior
       thompson.update(chosen_arm, reward)
    
    
       # Record the number of rewards and the chosen arm in each iteration
       rewards[t] = reward
       choices[t] = chosen_arm
    
    
       # At selected iterations, plot the current normal distributions.
       if (t+1) in snapshot_iters:
           plot_normal_posteriors(thompson, t+1)
    
    
    # At the end, show results
    print("Average reward:", np.mean(rewards))
    print("Number of pulls per arm:", thompson.n_pulls)
    print("True means:", [bandit.true_mean for bandit in bandits])
    

הממוצעים האמיתיים של 10 המודעות מוגדרים באמצעות מערך `true_means`.

בכל אחת מהאיטרציות:

• בוחרים את המודעה המניבה ביותר מהצעד הקודם. כשאין מידע כזה אז הבחירה באחת המודעות היא אקראית.

• דוגמאים את המודעה ("מציגים אותה") ומקבלים את הרווח שהיא מניבה נכון לאיטרציה הנוכחית.

• מעדכנים את ההסתברות הפוסטיריורית במידע החדש של כמה המודעה הרוויחה באיטרציה הנוכחית.

חוזרים על התהליך כמה שצריך. במקרה זה, הגדרתי 1000 איטרציות. בהתאמה למידת הקושי של המשימה.

• בכל אחת מהאיטרציות, מתעדים את הזרוע שנבחרה במסגרת האיטרציה, ואת הרווח שהניבה.

• אחרי שהלולאה מסיימת לרוץ, מציגים את ממוצע הרווחים ואת מספר הפעמים שהוצגה כל מודעה.

התוצאות:

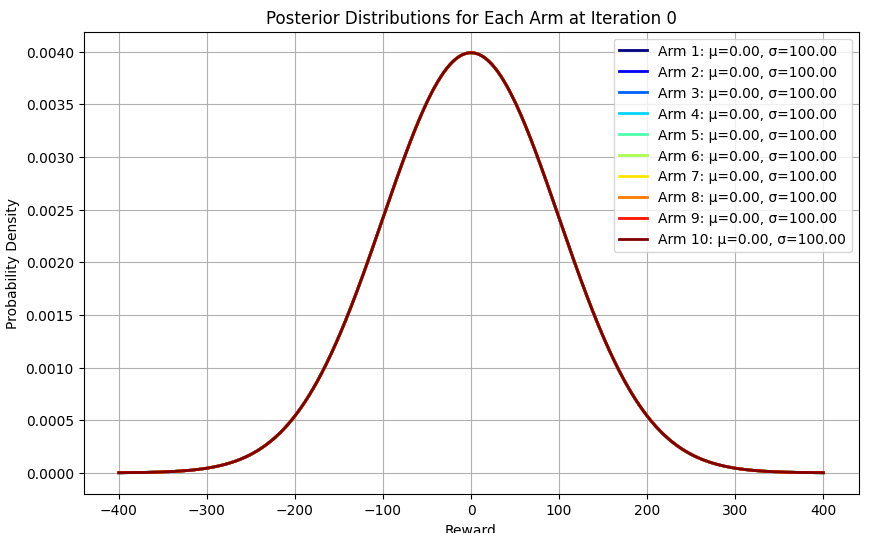
לפני שמריצים את הקוד, באיטרציה 0: כל הדוגמאות מקבלות ממוצע 0 ושונות 100 כי כך הגדרנו את ההתפלגות הפריורית המאוד רחבה שלנו.

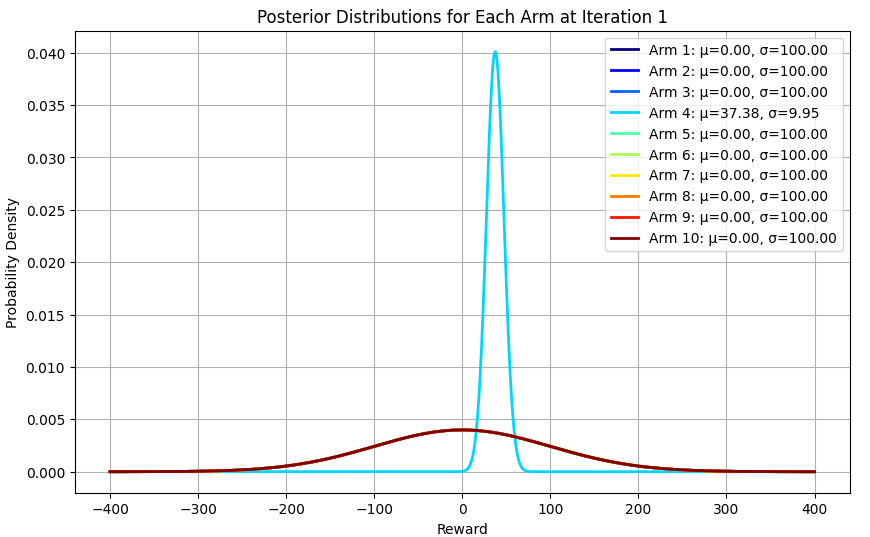
באיטרציה הראשונה: נבחרה מודעה 4 באקראי, והממוצע שלה עודכן ל-37 שזה לא כל כך רחוק מ-42 שהוא הממוצע האמיתי. כל יתר המודעות מתכנסות יחדיו עם ערך ממוצע 0 ושונות 100 כי טרם אספנו נתונים אודותיהם.

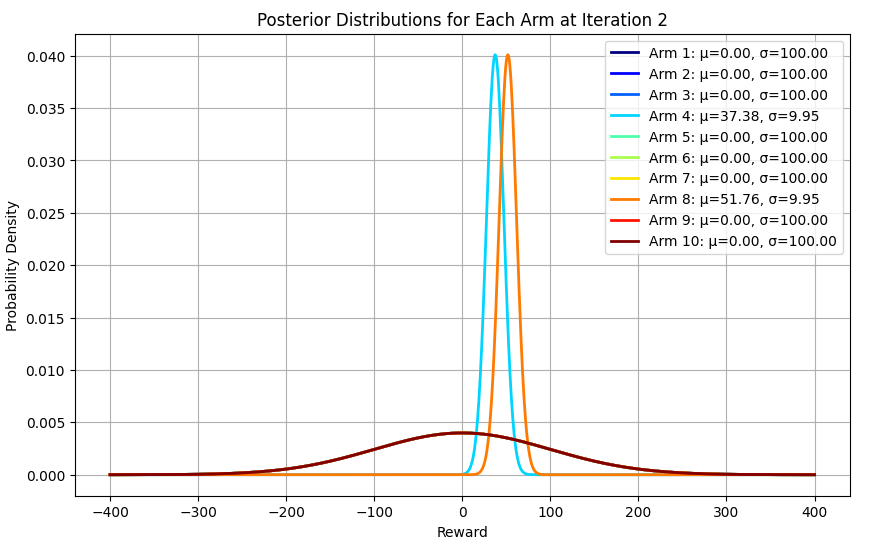
באיטרציה השנייה: נבחרה מודעה 8, שוב באקראי, והממוצע שלה עודכן ל-52, שוב די קרוב לממוצע האמיתי של 47.

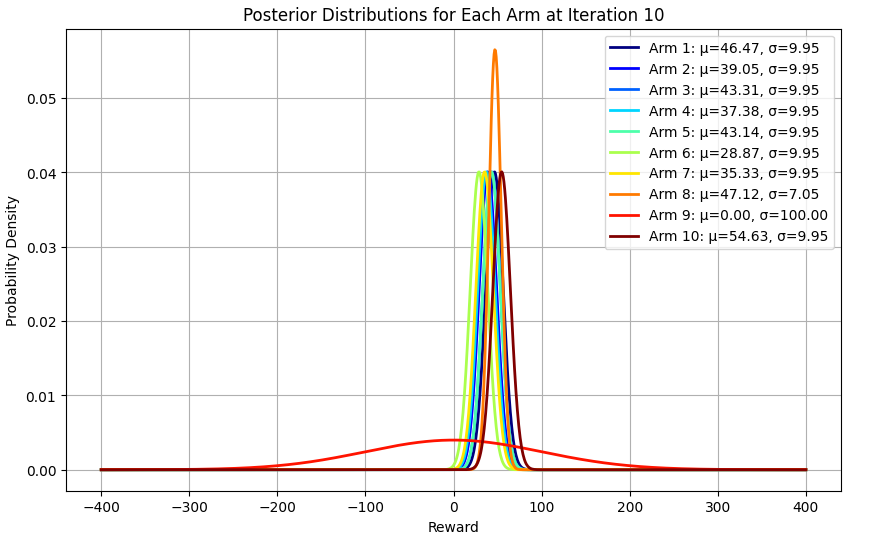
באיטרציה העשירית: נראה שכל המודעות, לבד מ-9, נבחרו והערך שלהם עודכן, וגם עושה רושם שהאלגוריתם מעדיף את מודעה 8 למרות שאנחנו יודעים שזו לא המודעה שנותנת את הרווח הגבוה ביותר.

באיטרציה 100: ניכר שהאלגוריתם מעדיף את מודעה 10 שהיא אכן המודעה הרווחית ביותר.

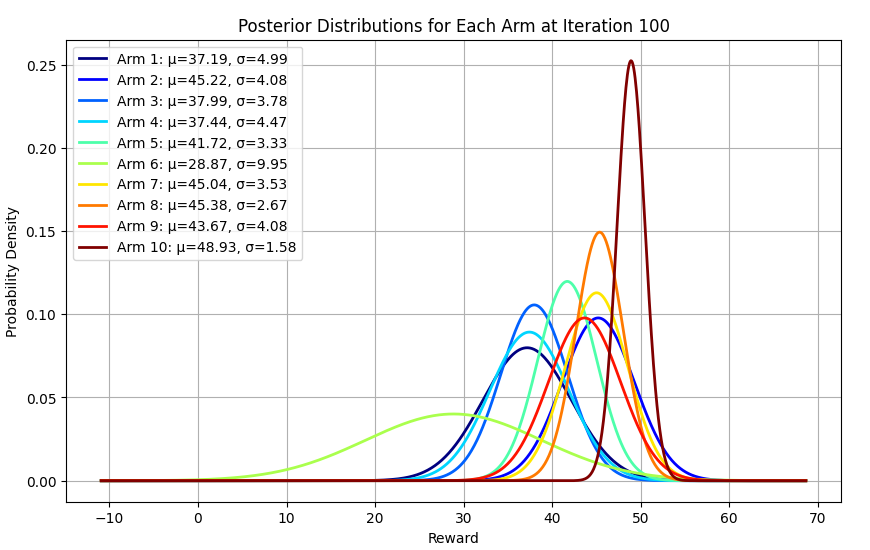
באיטרציות הבאות אנחנו יכולים לראות שמודעה 10 הולכת ונעשית הפייבוריטית תוך שהיא פותחת פער על כל היתר.

באיטרציה 1000: הפער הוא משמעותי כשמודעה 10 מובילה בפער גדול על כל היתר. המשמעות היא שרוב הדגימות העתידיות שהאלגוריתם יעשה יהיו של מודעה 10. בדיוק מה שאנחנו מצפים.

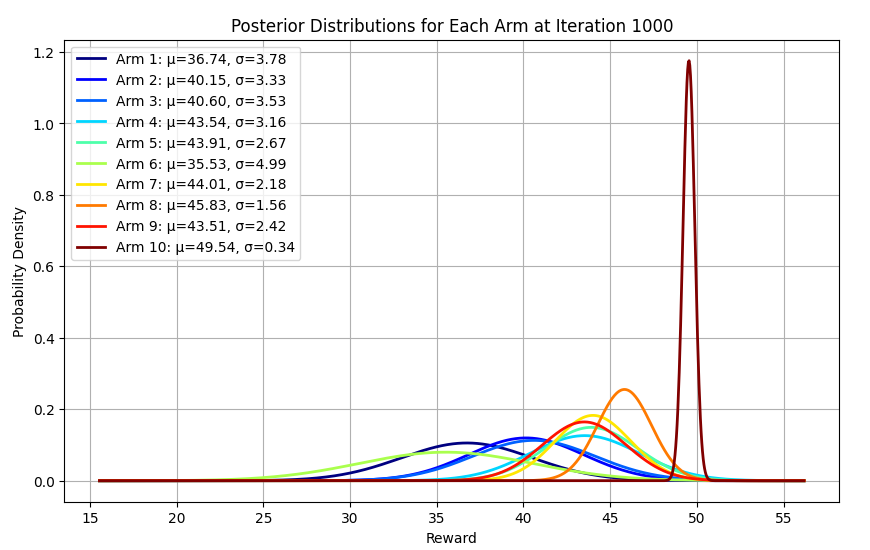
מעניין גם להסתכל על הממוצעים של המודעות ולראות שהאלגוריתם בטוח מאוד לגבי הממוצע של מודעה 10 עם שונות נמוכה יחסית ליתר המודעות של 0.3 וממוצע 49.5 שהוא מאוד דומה לממוצע האמת שהוא 49.

לגבי יתר המודעות השונות גבוהה יותר, בהתאמה למספר הנמוך יותר של פעמים בהם האלגוריתם בחן אותן:

Number of pulls per arm: [  7.   9.   8.  10.  14.   4.  21.  41.  17. 869.]

• 869 פעמים ניסה האלגוריתם את מודעה 10 והרבה פחות מכך את כל היתר.

יתרונות וחסרונות של Thompson Sampling

יתרונות:

• ניהול חוסר ודאות בצורה יעילה: האלגוריתם מצליח לאתר יחסית במהירות את החלופה הטובה יותר בסביבה של אי ודאות גדולה, ובכך מצליח לקצץ בעלויות, ולאזן באופן חכם בין חקר לניצול.

• התאמה מתמשכת: האלגוריתם מעדכן באופן רציף את הערכותיו ככל שהוא צובר יותר נתונים, מה שמאפשר לו להתאים את החלטותיו לסביבה משתנה.

• פשטות ואינטואיטיביות: קל להסביר ולהבין את האלגוריתם.

חסרונות:

• עומס חישובי: ניהול ועדכון של מספר גדול של חלופות עלול להיות יקר חישובית בסביבות מורכבות.

• תלות בהנחות מקדימות: בחירת ההנחות המקדימות עלולה להשפיע על הביצועים בסיבובים הראשונים כאשר בחירה של prior לא מתאים עלולה לגרום לעיכוב בהתכנסות.

• סיכון לקיבעון בנקודות קיצון מקומיות: אף על פי שחקר exploration מובנה באלגוריתם, עדיין קיימת סכנת התכנסות לאופטימום מקומי, כאשר האלגוריתם חוזר שוב ושוב לחלופה רק בגלל שבמקרה היא נראית הטובה ביותר בסיבובים הקודמים אף שאינה כזו.

יישומים של Thompson sampling בעולם האמיתי

הודות לפשטות ולאינטואיטיביות של אלגוריתם דגימת תומפסון Thompson sampling נמצאו לה שימושים רבים, ובכלל כך:

• פרסום דיגיטלי: בחירת המודעה האופטימלית למקסום הרווח.

• ניסויים קליניים: הקצאת מטופלים לטיפולים באופן שממקסם את התועלת הכוללת.

• מערכות המלצה: התאמה אישית של תכנים למשתמשים באמצעות חקר אפשרויות שונות.

• בעיות קונטקסטואליות (Contextual Bandits): שילוב מידע קונטקסטואלי (כמו נתוני משתמש) לקבלת החלטות מושכלות יותר.

• שיטות היברידיות: שילוב Thompson Sampling עם אסטרטגיות חקר נוספות (כמו epsilon-greedy) כדי להקטין את הסיכון לקיבעון לאופטימום מקומי. לדוגמה, אפשר להשתמש בדגימת תומפסון ב-90% מהמקרים, וב-10% בepsilon-greedy.

לסיכום

שיטת דגימת תומפסון Thompson sampling מהווה כלי חזק ואינטואיטיבי להתמודדות עם האתגר של איזון בין חקר לניצול בבעיות קבלת החלטות סדרתיות. באמצעות עקרונות בייס Bayes ועדכון מתמיד של האמונות לגבי הרווח שניתן להפיק מכל זרוע, השיטה מצליחה להתאים את עצמה לסביבה משתנה ולמצוא את הפתרון האופטימלי תוך כדי למידה מהנתונים.

ממליץ לשחק עם הקוד, להסיר ולהוסיף בנדיטים, להגדיל את הריווח בין ממוצעי המודעות, לשנות את הנחות הבסיס, את ה-seed, וכיו"ב כדי לקבל תחושה לגבי הדינמיקה של מציאת הזרוע העדיפה כאשר משתמשים באלגוריתם דגימת תומפסון.

אולי גם זה יעניין אותך

התפלגות בטא ותהליך העדכון הבייסיאני

איך למצוא את מספר הדוגמאות הדרושות ללמידת מכונה?

מבחנים סטטיסטיים עבור בדיקת A/B באמצעות פייתון

לכל המדריכים בנושא של למידת מכונה

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים