אלגוריתם חיפוש בינארי - מהבנה ליישום

חיפוש בינארי הינו אלגוריתם חיפוש מהיר. כמה מהיר? מספיק 30 פעולות כדי למצוא בוודאות פריט ברשימה בת מיליארד פריטים. רוצה לדעת עוד על השיטה וכיצד ליישם אותה בפייתון?

נאמר שיש לך מסד נתונים עם שמות משתמש ואתה מחפש את המשתמש "ירובעל". שמות המשתמשים מסודרים בסדר הא"ב. האפשרות הפשוטה ביותר היא לחפש לפי סדר הא"ב. מתחילים לחפש ב-א' ואז עוברים על כל השמות המתחילים ב-א'. אח"כ עוברים ל-ב'. אח"כ ל-ג'. וכיו"ב. המחשבים היום מספיק מהירים וברשימה של כמה מאות שמות לא תרגיש שיש בעיה אבל מה לגבי מסד נתונים עם מיליוני שמות. דרך טובה יותר היא להתחיל באמצע הרשימה כי שמות המתחילים ב-"י" צפויים להימצא במחצית הרשימה פחות או יותר.

נראה דוגמה נוספת. נאמר שאני מבקש ממך לנחש על איזה מספר אני חושב בטווח של 1 עד 100. אתה יכול לנחש כל אחד מהמספרים בטווח. אתה יכול לחפש באופן ליניארי ולעבור על כל רשימת המספרים: 1, 2, 3, 4, 5, 6, וכיו"ב. במקרה הגרוע בו בחרתי 100 תצטרך 99 ניחושים כדי למצוא את המספר עליו אני חושב.

דרך טובה יותר היא לנחש את המספר באמצע: 50. אם ניחשת גבוה מדי אז לנחש 25 כי הוא בדיוק באמצע בין 1 ל-50. אם הניחוש החדש נמוך מדי אז לנחש מספר שהוא באמצע בין 25 ל-50 שזה 37. בכל פעם שמנחשים בוחרים מספר הנמצא באמצע הטווח הגבוה יותר או הנמוך יותר עד שמוצאים את מה שמחפשים. בכל פעם שמחפשים מחדש הטווח שמתוכו יש לנחש מצטמצם לחצי. בגישה הזו חוסכים המון ניחושים.

הגישה הזו מכונה חיפוש בינארי binary search.

חיפוש בינארי מחזיר את מיקומו של אלמנט במערך מסודר. חובה שהמערך יהיה מסודר!

נסתכל על המקרה הגרוע ביותר בו לא נצליח למצוא את הפריט המבוקש:

צריך לנחש מתוך רשימה בת 100 פריטים > לא מצאנו ועל כן נצמצם לרשימה של 50 פריטים > נצמצם ל- 25 פריטים > 13 > 7 > 4 > 2 > 1

בגישה של חיפוש בינארי צריך לנחש לכל היותר 7 פעמים לעומת 99 ניחושים כאשר משתמשים בחיפוש לינארי פשוט.

אפשר להגיע למסקנה שצריך לנחש לכל היותר 7 פעמים על ידי שימוש בלוג בסיס 2 שנוסחתו:

log2(n)

• כאשר n מייצג את מספר הפריטים ברשימה.

למה log בסיס 2 ולא משהו אחר? הרי בד"כ אנחנו רגילים לבסיס 10.

זה בגלל שאנחנו מחלקים את הרשימה בכל פעם ל-2.

נפעיל לוג בסיס 2 על 100 כדי לראות כמה פעולות בינאריות יידרשו לכל היותר על רשימה בת 100 פריטים:

log2(100) = 7

• 7 ניחושים. 7 חזרות על תהליך החיפוש יספיקו כדי למצוא את הפריט במקרה הגרוע ביותר.

עכשיו נאמר שברשימה יש 200 פריטים במקום 100. כמה ניחושים נצטרך לכל היותר כדי למצוא את מה שאנחנו מחפשים?

log2(200) = 8

מה קורה אם צריך לאתר רשומה 1 בתוך מסד נתונים של מיליון שמות? אז אפשר להגיע עד ל-999,999 ניחושים בגישה לינארית או לכל היותר 20 בגישה של חיפוש בינארי. כאשר:

log2(1000000) = 20

מה לגבי מסד נתונים ובו מיליארד רשומות:

log2(1000000000) = 30

• צריך לחזור לכל היותר 30 פעמים על תהליך החיפוש הבינארי כדי לאתר בוודאות רשומה מסוימת במסד נתונים המונה 1,000,000,000 רשומות. בגישה לינארית היינו צריכים לכל היותר לנחש מיליארד פעמים. 

נאמר שמחשב צריך לעשות את החיפוש ושמשך כל פעולה הוא אלפית השנייה (מילי שנייה) אז משך החיפוש בגישה של חיפוש בינארי הוא 30 מילי שניות ובגישה של חיפוש לינארי 11.5 ימים!!!

עד כה הדגמנו את יתרונות החיפוש הבינארי. בוא נראה איך עובד האלגוריתם.

במדריך זה נדגים אלגוריתם חיפוש בינארי על מערכים.

מערכים קוראים משמאל לימין.

לדוגמה המערך הבא:

כשעובדים עם מערכים חשוב להבחין בין ערכים ובין אינדקסים. הערכים זה מה שמוצב בתוך כל פריט במערך. האינדקס הוא מספר סודר המתחיל מאפס, ואח"כ בסדר עולה: 0, 1, 2, 3, 4…

• במקרה שלנו, הערך המוצב באלמנט הראשון (אינדקס 0) הוא 1. הערך המוצב באינדקס 1 הוא 2. הערך באינדקס 2 הוא 3. וכיו"ב.

נסכם באמצעות טבלה:

מהו אלגוריתם חיפוש בינארי וכיצד הוא עובד

הרעיון של חיפוש בינארי הוא לחפש התאמה בתוך טווח. מתחילים מטווח הכולל את כל המערך. מחלקים את המערך לשניים סביב נקודת האמצע. אם ערך האלמנט האמצעי שווה למה שמחפשים אז מחזירים את מיקום האינדקס. אחרת מצמצמים את טווח החיפוש. אם הערך אותו מחפשים גבוה יותר אז מחפשים בחצי המערך המכיל את הערכים הגבוהים. אם הערך אותו מחפשים נמוך יותר, מחפשים בחצי המכיל את הערכים הנמוכים. וחוזר חלילה מצמצמים את טווח החיפוש בכל פעם פי 2 עד שמגיעים למערך שאורכו 1. אם המערך מכיל את הערך הרצוי אז מחזירים את האינדקס שלו. אחרת מה שאנחנו מחפשים לא נמצא במערך.

חיפוש בינארי מבוסס על גישת "הפרד ומשול" - מחלקים בעיה גדולה לבעיות משנה. פותרים את בעיות המשנה. בסוף פותרים את הבעיה הגדולה על ידי שילוב כל הפתרונות לבעיות המשנה.

כדי לעשות חיפוש בינארי נחלק את המערך לשניים סביב נקודת האמצע. אם ערך האלמנט האמצעי שווה למה שמחפשים אז מחזירים את מיקום האינדקס. אם הערך אותו מחפשים גבוה יותר מתחילים לחפש מהאלמנט הראשון הבא אחרי נקודת האמצע. אם הערך אותו מחפשים נמוך יותר, מגבילים את החיפוש עד לאלמנט האחרון הבא לפני נקודת האמצע. וחוזר חלילה עד שמגיעים למערך באורך פריט 1.

במדריך זה נציג שתי גישות ליישום של חיפוש בינארי: באמצעות לולאה iterative approach ובאמצעות רקורסיה recursive approach

שתי הגישות מיישמות את אותה סדרה של פעולות באמצעים שונים.

נתחיל מהדגמה של חיפוש בינארי על מערך של 6 מספרים מסודרים מ 1-6. נחפש את הערך 5. זה יהיה ערכו של המשתנה s אותו נחפש.

1. נתחיל ממערך מסודר arr, וערך אותו יש לחפש, s = 5.

   

2. נשתמש בשני מצביעים התוחמים את טווח החיפוש. אחד המכוון על האינדקס הנמוך ביותר של המערך (מכונה LO) ושני המכוון על האינדקס הגבוה ביותר (HI).

   

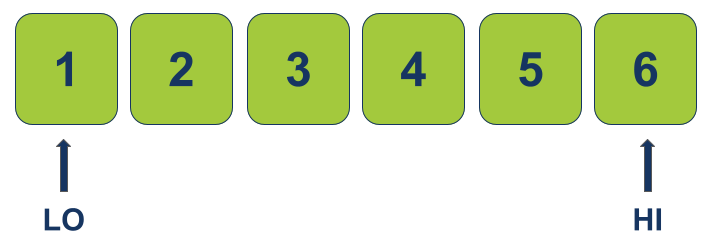
   • מתחילים ממצב בו טווח החיפוש כולל את כל האלמנטים במערך.
   • האלגוריתם מחפש בין שני המצביעים כל עוד LO אינו גבוה מ-HI.

3. נמצא את נקודת האמצע של המערך (אותה נכנה MID):

   

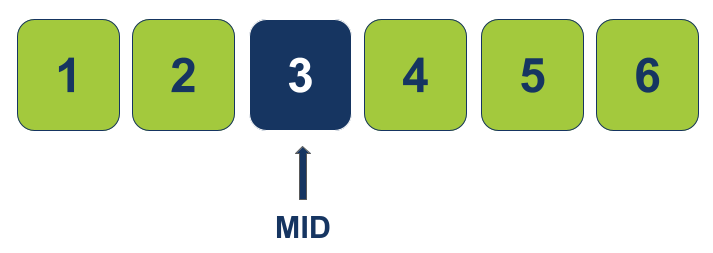
   • במקרה זה המערך הוא בעל מספר זוגי של אלמנטים על כן נעגל מטה כדי למצוא את נקודת האמצע.
   • האינדקס של נקודת האמצע MID הוא 2 והערך שלו הוא 3.
4. • אם הערך של MID היה שווה לערך אותו אנו מחפשים (s=5) היינו מחזירים את האינדקס ומסיימים את החיפוש.
   • אם הערך s אותו אנו מחפשים היה נמוך יותר מ-MID היינו מעדכנים את המצביע HI כדי שיצביע על האינדקס הסמוך הנמוך מנקודת האמצע MID-1 כדי להמשיך את החיפוש בחצי המכיל את הערכים הנמוכים יותר.
   • במקרה שלנו, הערך s גדול יותר מ-MID ועל כן נעדכן את המצביע LO כדי שיהיה ממוקם באינדקס הבא אחרי נקודת האמצע MID+1 כדי שנחפש בחלק של המערך בו המספרים גבוהים יותר מ-MID.

   

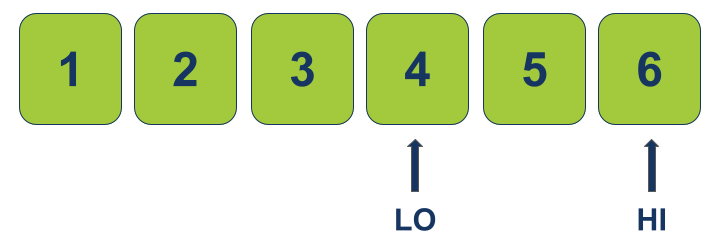
5. נחזור על התהליך: 

   נקודת האמצע החדשה MID בתוך הטווח שבין LO החדש ו-HI נמצאת באינדקס 4 וערכה 5.

   כיוון שהערך 5 שווה לערך s אותו אנו מחפשים, נחזיר את האינדקס (4), ונסיים את החיפוש.

   

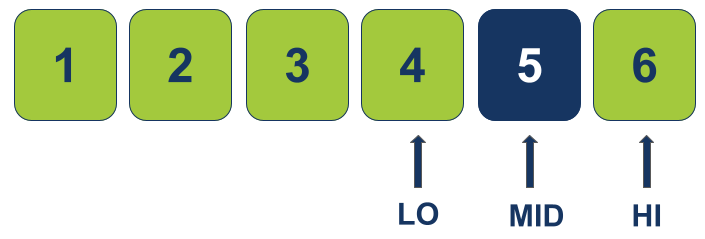
6. במידה ותהליך החיפוש לא היה מוצא התאמה האלגוריתם היה מחזיר -1. זה היה קורה אילו התהליך היה מצמצם את טווח החיפוש עד למערך שיש בו פריט 1 לכל היותר, ומה שנשאר מהמערך לא היה מה שמחפשים.

 

קוד פייתון לביצוע חיפוש בינארי

נראה את הקוד של שתי הגישות ליישום של חיפוש בינארי:

1. באמצעות לולאה iterative approach
2. באמצעות רקורסיה recursive approach

קוד פייתון המיישם חיפוש בינארי בגישה איטרטיבית (באמצעות לולאה):

# iterative approach
def bin_search(arr, s):
   # lowest index to search in
   lo = 0
  
   # highest index to search
   hi = len(arr) - 1
  
   while lo <= hi:
       # current index at the median position
       # rounded down if mid isn't even
       mid = (lo+hi)//2
      
       # if current array item
       # equals "s" return current index
       # since "s" is in the array you finished searching
       # and you return the index
       if s == arr[mid]:
           return mid
      
       # if "s" is smaller than current item
       # update the highest index
       # so the the search in the next iteration
       # will be in the left part of the array
       if s < arr[mid]:
           hi = mid-1
          
       # if "s" is larger than current item
       # update the lowest index
       # so the search is in the right
       # part of the array
       elif s > arr[mid]:
           lo = mid+1
   
   # the search didn't find "s" in the array
   # so return a default index value of -1 
   return -1

נבדוק:

# Test cases
arr = [0, 1, 3, 4, 6]

for target in range(-1, 8):
    print(f"Target {target} in index {bin_search(arr, target)}")

empty_arr = []
print(f"Target 1 in empty array: {bin_search(empty_arr, 1)}")

 

קוד המיישם חיפוש בינארי בגישה רקורסיבית:

def r_bin_search(arr, target):
    
    if not arr: 
        return -1
    
    # Helper function
    def search(lo, hi):
        # Base case
        if lo > hi:
            return -1 
        
        mid = (lo+hi)//2
        
        # Recursive case
        if arr[mid] == target:
            return mid
        elif target > arr[mid]:
            return search(mid+1, hi)
        else:
            return search(lo, mid-1)

    # Call to the helper function from the wrapper function
    return search(0, len(arr)-1)

• הפונקציה העוטפת r_bin_search() קוראת לפונקציה הפנימית search() שהיא זו שעושה את החיפוש בפועל באמצעות רקורסיה.

  

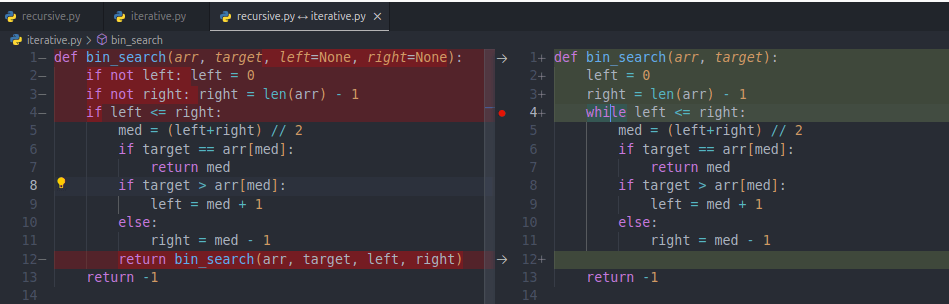
השוואה התחביר לביצוע חיפוש בינארי בגישות איטרטיבית ורקורסיבית

צילום המסך הבא של עורך הקוד שלי vscode משווה בין הסקריפטים לביצוע חיפוש בינארי בגישה איטרטיבית ורקורסיבית. מהשוואה זו אפשר לראות עד כמה התחביר הוא דומה:



  

משך הזמן לביצוע

במקרה הטוב ביותר	O(1)
במקרה הממוצע	O(logN)
במקרה הגרוע ביותר	O(logN)

 

המקום בזכרון הדרוש לביצוע חיפוש בינארי

space complexity

O(1)

space complexity - כמות המקום בזכרון הדרוש לביצוע התהליך במלואו.

משך הזמן לביצוע האלגוריתם במקרה הטוב ביותר הוא :

O(1)

 

הסבר על ביצועי האלגוריתם

המקרה הגרוע ביותר big O מבחינת משך הזמן בחיפוש בינארי הוא כאשר אנחנו מצמצמים את טווח החיפוש בכל פעם בחצי עד שאנחנו מגיעים לפריט אחד במערך ומגלים שזה אינו הערך אותו אנו מחפשים. בגלל שאנחנו מצמצמים בחצי מקסימום ההשוואות שנעשה הוא logN. מכאן שמשך הביצוע של המקרה הגרוע ביותר הוא לוג התלוי במספר הפריטים במערך:

O(log N)

נסתכל על מערך המונה 8 פריטים. חוצים את המערך פעם אחת ומקבלים 2 מערכים של 4. חוצים כל אחד מהמערכים ומקבלים 4 מערכים של 2. חוצים כל אחד מהמערכים שיש להם 2 פריטים ומקבלים פריט אחד במערך. וזהו אי אפשר יותר לחצות, מיצינו. ביצענו בסה"כ 3 פעולות של חצייה לשניים עבור 8 פריטים בהתאם לעובדה ש- 2 בחזקת 3 הם 8. מכאן הקשר הלוגריתמי כי הלוגריתם בסיס 2 שואל באיזה חזקה יש להעלות את 2 כדי לקבל 8.

הזמן הממוצע מוגדר כסכום כל זמני החיפוש האפשריים חלקי מספר האפשרויות:

Avg. case = sum possible case times / no. of cases

בוא נראה מהם אפשרויות החיפוש:

• אם הערך שאנו מחפשים נמצא בדיוק באמצע המערך אז נבצע פעולת השוואה 1.
• אם הערך נמצא בדיוק באמצע אחד מ-2 המערכים (=המקרים) אחרי החלוקה הראשונה אז נגיע לזה אחרי ביצוע 2 השוואות. 
• אם הערך נמצא בדיוק באמצע של אחד מ-4 מערכים (=מקרים) אחרי חלוקה שנייה אז נגיע לזה אחרי 3 השוואות.
• וכיו"ב

יש לנו דפוס. מספר המקרים הדורשים i השוואות הוא 2 בחזקת (i-1):

2^(i-1)

מספר המערכים (=המקרים) המקסימלי הוא logN. ובמקרה זה נבצע את מספר הפעולות הבא ע"פ הכלל אותו ניסחנו לעיל:

2^(logN-1)

נסכם את מספר מקרי החיפוש האפשריים:

Sum possible case times = 1*1 + 2*2 + 3*4 + … + logN * 2^(logN-1)

נפעיל את חוקי הלוגריתמים ונזניח את הקבועים כדי לקבל:

Sum possible case times = N * log(N)

מספר המקרים הוא N.

נסיק את זמן הביצוע הממוצע ע"פ הנוסחה:

Avg. case = sum possible case times / no. of cases

ונקבל:

Avg. case time complexity = N * log(N) / N = log(N)

לפיכך, הזמן הממוצע מבחינת משך זמן ביצוע החיפוש הבינארי הוא:

O(log N)

• בדיוק כמו זמן הריצה הארוך ביותר.

  

מבחינת מקום space complexity של חיפוש בינארי הוא O(1) כיוון שהמחשב לא צריך להקצות מקום נוסף בזכרון כדי לבצע את החיפוש.

 

חידה

כמו שכתבתי בכותרת אנחנו לא רק נבין את האלגוריתם אלא גם נלמד ליישם אותו בקוד כשצריך לשים שבכל פעם שאנו מקבלים רצף מסודר בתור קלט צריך להעדיף את השימוש בחיפוש בינארי על פני חיפוש לינארי כי הוא הרבה יותר יעיל.

החידה הולכת ככה:

נותנים לנו מערך מסודר של מספרים ומספר מטרה. המערך עשוי להכיל ערכים כפולים או מספרים שליליים. מטרתנו היא למצוא מספר במערך שהוא הקרוב ביותר למספר המטרה.

דוגמה ראשונה:

Input : arr = [1, 2, 4, 3, 4, 5]
Input : target = 42
Output : 5
Explain: 5 is closest to 42 in the array

דוגמה שנייה:

Input : arr = [6, 7, 13, 42]
Input : target = 8
Output : 7
Explain: 7 is closest to 8 in the array

נסה להשתמש בידע שצברת במדריך על חיפוש בינארי כדי לפתור את הבעיה.

אל תציץ בתוצאות כי אם תציץ בתוצאות יוטל עליך חרם 😄 קודם כל תנסה לבד.

ניסית לבד? אתה מוזמן לקרוא את הפתרון שאני מציע:

def find_closest(arr, target):
    """
    This function finds the closest number to a given target number 
    in a sorted array with the help of binary search.
    
    If you have sorted sequence you need to consider using the 'binary search'
    algo over the linear search because it is much more efficient.

    Args:
        arr: The sorted array.
        target: The target number.

    Returns:
        The closest number to the target number in the array.
    """
    
    # Check if the array is empty. If it is, return None.
    if len(arr) == 0:
        return None
    
    # Initialize the lower and upper bounds of the search.
    lo = 0
    hi = len(arr) - 1
    
    # Loop while the lower bound is less than or equal to the upper bound.
    while lo <= hi:
        # Calculate the middle index of the array.
        mid = (lo+hi)//2
        
        # If the target number is equal to the element at the middle index, 
        # return the element.
        if target == arr[mid]:
            return target
        
        # If the target number is less than the element at the middle index, 
        # set the upper bound to the middle index minus 1.
        if target < arr[mid]:
            hi = mid-1

        # If the target number is greater than the element at the middle index, 
        # set the lower bound to the middle index plus 1.
        elif target > arr[mid]:
            lo = mid+1
            
    # If the lower bound is greater than or equal to the length of the array, 
    # return the element at the lower bound.
    if len(arr) <= lo:
        return arr[lo - 1]
    
    # Calculate the absolute difference between the target number 
    # and the elements at the upper and lower bounds.
    delta_lo = abs(target - arr[lo])
    delta_hi = abs(target - arr[hi])
    
    # Return the element with the smaller absolute difference.
    if delta_lo <= delta_hi:
        return arr[lo]
    else:
        return arr[hi] 

נבדוק שהפונקציה עובדת בכל מיני תנאים, ואז נסביר אותה.

ננסה את הפתרון:

arr = [1, 2, 4, 5, 6, 6, 8, 9]
target = 123
print(find_closest(arr, target))

התוצאה:

9

תמיד חשוב לבדוק את הקוד בכל מיני מבחנים ועבור כמה שיותר תנאים במיוחד תנאי קצה:

def test_find_closest():
    # Test with a sorted array that contains the target number.
    arr = [1, 2, 3, 4, 5]
    target = 3
    print(find_closest(arr, target)) # 3

    # Test with a sorted array that does not contain the target number.
    arr = [1, 2, 3, 4, 5]
    target = 6
    print(find_closest(arr, target)) # 5

    # Test with a sorted array that does not contain the target number.
    arr = [1, 2, 3, 4, 5]
    target = -1
    print(find_closest(arr, target)) # 1

    # Test with a sorted array that contains duplicate values.
    arr = [1, 2, 2, 3, 4]
    target = 2
    print(find_closest(arr, target)) # 2

    # Test with a fractional number.
    arr = [1, 2, 2, 3, 4]
    target = 2.8
    print(find_closest(arr, target)) # 3

    # Test with a fractional number.
    arr = [1, 2, 2, 3, 4]
    target = 2.1
    print(find_closest(arr, target)) # 2

    # Test with an empty array.
    arr = []
    target = 1
    print(find_closest(arr, target)) # None

    # Test with a array with one element.
    arr = [1]
    target = 847
    print(find_closest(arr, target)) # 1

    # Test with a array with one element.
    arr = [1]
    target = -847
    print(find_closest(arr, target)) # 1

    # Test with a array with negative numbers.
    arr = [-1, 0, 1]
    target = 0
    print(find_closest(arr, target)) # 0

test_find_closest()

נסביר את הפונקציה:

1. הפונקציה "find_closest" מקבלת שני ארגומנטים: מערך ומספר מטרה. הפונקציה מחזירה את המספר במערך הקרוב ביותר למספר המטרה.
2. ראשית, הפונקציה בודקת אם המערך הוא ריק. במקרה זה היא מחזירה None.
3. בהמשך, הפונקציה מאתחלת שני משתנים lo ו-hi. כאשר lo הינו האינדקס של הפריט הראשון במערך בעוד hi הוא האינדקס של הפריט האחרון.
4. הפונקציה נכנסת ללולאת while אשר רצה עד ש-lo משתווה ל- או גבוה מ- hi.
5. בתוך הלולאה, הפונקציה מחשבת את האינדקס האמצעי של המערך אשר מחושב על ידי חיבור hi עם lo וחלוקה ב-2.
6. הפונקציה בודקת אם מספר המטרה שווה לפריט באינדקס האמצעי. אם הוא שווה, הפונקציה מחזירה את ערכו של הפריט.
7. אם מספר המטרה אינו שווה לפריט באינדקס האמצעי, הפונקציה בודקת אם מספר המטרה קטן או גדול מהאינדקס האמצעי. אם מספר המטרה קטן יותר, הפונקציה מגדירה את hi כשווה לאינדקס האמצע פחות 1. אם מספר המטרה גדול יותר, הפונקציה מגדירה את lo על פי האינדקס האמצעי בתוספת 1.
8. כאשר הלולאה מסיימת לרוץ, היא בודקת האם lo גדול או שווה מאורך המערך. אם זה המצב הפונקציה מחזירה את הערך האחרון במערך כי אין מספר במערך הקרוב יותר לערך המטרה.
9. הפונקציה מחשבת את ההפרש האבסולוטי בין ערך המטרה לבין ערכי הפריטים של המערך עליהם מצביעים lo ו-hi
10. הפונקציה מחזירה את הפריט של המערך שיש לו את ההפרש האבסולוטי הנמוך ביותר כיוון שהוא המספר הקרוב ביותר למספר המטרה.

 

סיכום

חיפוש בינארי מהיר יותר מחיפוש לינארי בגלל שמשך הביצוע גדל באופן לוגריתמי. ככל שהקלט input גדול יותר כך גדל ההבדל. קושי אחד ביישום הוא הצורך של הקלט להיות מסודר מה שאומר שפריטי הקלט צריכים להיות ניתנים לסידור וגם שיש צורך לסדר אותם לפני ביצוע החיפוש מה שמוסיף עומס למערכת.

  

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

big-O ביטוי ליעילות הקוד

רקורסיה בפייתון - כל מה שרצית לדעת, ועוד כמה דברים חשובים

args ו-kwargs בפייתון מוסברים בשפה פשוטה

מדריך map, filter, reduce

 

לכל המדריכים בסדרה ללימוד פייתון

 

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים