רקורסיה בפייתון - כל מה שרצית לדעת ועוד כמה דברים חשובים

רקורסיה היא טכניקה תכנותית במסגרתה פונקציה קוראת לעצמה עד שהיא מפסיקה. לטכניקה זו שימושים רבים, ובכלל כך פתרון בעיות בגישה של "הפרד ומשול" כאשר מפרקים בעיה מסובכת וגדולה לבעיות קטנות שקל לפתור. במדריך זה נראה כמה דוגמאות לרקורסיה, נסביר כיצד היא עובדת, נציג את יתרונותיה ומגבלותיה, וכיצד להתמודד עם המגבלות.

חישוב סכום מערך באמצעות רקורסיה

האתגר הוא לכתוב פונקציה לסיכום כל המספרים במערך. לדוגמה, בהינתן רשימת מספרים:

[1, 2, 3]

סכום המספרים הוא:

1 + 2 + 3 = 6

כדי לפתור באופן רקורסיבי, נשאל את עצמנו מהו המקרה הפשוט ביותר שאותו אנחנו יכולים לפתור. במקרה שלנו, מה יקרה אם הפונקציה הסוכמת תקבל קלט של מערך ריק, ללא איברים. במקרה, של מערך ריק היא תחזיר סכום 0 כי אין לה מה לסכום. נכתוב את זה:

if len(arr) == 0:
        return 0

ומה קורה אם הפונקציה מקבלת קלט של מערך באורך פריט יחיד? במקרה כזה, נוסיף את הפריט היחיד לסכום.

ומה קורה אם הפונקציה מקבלת מערך באורך כמה פריטים? עם זה אנחנו לא יודעים להתמודד אבל אנחנו כן יודעים להתמודד עם פריט יחיד אז נפלוט את הפריט מסוף המערך כדי להפוך אותו לפריט יחיד, ואת הפריט היחיד נוסיף לסכום. נכתוב את זה:

# Get the last element
last_item = arr.pop() 
sum = sum + last_item

• הקוד מסיר את הפריט האחרון ומוסיף לסכום.

אבל מאיפה נקבל את הסכום? בשביל לקבל את הסכום אנחנו יכולים לקרוא לפונקציה סוכמת:

def recur_sum(arr):
      # Calculate sum recursively

מה הפונקציה הסוכמת תעשה? אנחנו יודעים. במקרה של מערך ריק היא תחזיר 0, ובכל יתר המקרים היא תסיר את הפריט האחרון ותוסיף לסכום. נכתוב את זה:

def recur_sum(arr):
    if len(arr) == 0:
        return 0
    else:
          last_item = arr.pop() 
          return last_item + sum

אבל מאיפה מגיע הסכום? הוא מגיע מזה שהפונקציה קוראת לעצמה על המערך הנותר לאחר הסרת הפריט האחרון מן המערך:

def recur_sum(arr):
    if len(arr) == 0:
        return 0
    else:
        last_item = arr.pop() 
        return last_item + recur_sum(arr)  

נראה שכתבנו פונקציה. אולי היא אפילו עובדת. נבחן אותה:

print(recur_sum([])) # 0
print(recur_sum([1])) # 1
print(recur_sum([1, 2])) # 3
print(recur_sum([1, 8, 5])) # 14

• הפונקציה `recur_sum()` פותרת את הבעיה של סכימת מערך של מספרים על ידי כך שהיא עובדת בשלבים. בכל שלב, היא מסירה את הפריט האחרון מן המערך ומוסיפה לסכום יתר פריטי המערך.

הפונקציה הרקורסיבית שכתבנו מכילה 2 חלקים, מקרה בסיס ומקרה רקורסיבי:

def recur_sum(arr):
    # Base case
    if len(arr) == 0:
        return 0
    else:
        # Recursive case
        last_item = arr.pop() 
        return last_item + recur_sum(arr)

מקרה הבסיס מגדיר באילו תנאים הפונקציה צריכה להפסיק את הקריאות לעצמה. במסגרת המקרה הרקורסיבי הפונקציה קוראת לעצמה על גרסה של הבעיה המקורית.

מקרה הבסיס מגדיר באילו תנאים הפונקציה צריכה להפסיק את הקריאות לעצמה. במסגרת המקרה הרקורסיבי הפונקציה קוראת לעצמה על גרסה של הבעיה המקורית.

בפונקציה שלנו, במקרה הבסיס, הפונקציה מחזירה 0 כיוון שהיא מקבלת קלט של מערך ריק. במקרה הרקורסיבי, הפונקציה מסירה את הפריט האחרון של המערך, ואז קוראת לעצמה (=באופן רקורסיבי) עבור הגרסה המקוצרת של המערך.

כאשר קוראים לפונקציה recur_sum() בפעם הראשונה עם רשימה כמו [1, 2, 3, 5], היא מתחילה במקרה הרקורסיבי מכיוון שאורך הרשימה אינו אפס. היא אז פולטת pop() את הפריט האחרון (5) ומבצעת קריאה רקורסיבית לעצמה על הרשימה המקוצרת [1, 2, 3]. בקריאה הרקורסיבית הבאה, היא פולטת 3 וקוראת לעצמה עם המערך [1, 2]. תהליך זה נמשך עד שמגיעים למקרה הבסיס עם רשימה ריקה ([]). בשלב זה, הרקורסיה נעצרת, וכל הקריאות הרקורסיביות מוחזרות. כאשר הקריאות מוחזרות, הפונקציה סוכמת את הערכים ומחזירה את התוצאה הסופית, סכום כל הפריטים ברשימה המקורית: 5 + 3 + 2 + 1 = 11.

נסכם.

פונקציה רקורסיבית מורכבת משני חלקים, משני מקרים:

1. מקרה בסיס: לכל פונקציה רקורסיבית צריך להיות מקרה בסיס או תנאי סיום. זה התנאי שבו הרקורסיה נעצרת. כאשר מקרה הבסיס מתקיים, הפונקציה מחזירה תוצאה מבלי לבצע קריאות רקורסיביות נוספות. ללא מקרה בסיס, הרקורסיה תמשיך לרוץ ללא הגבלה, מה שיגרום להצפת זכרון stack overflow.
2. מקרה רקורסיבי: בנוסף למקרה הבסיס, פונקציה רקורסיבית מכילה גם מקרה רקורסיבי אחד או יותר. אלו המקרים שבהם הפונקציה קוראת לעצמה עם גרסה שעברה שינוי של הבעיה המקורית. הרעיון הוא לחלק את הבעיה לתת-בעיות קטנות טריוויאליות, דומות אחת לשנייה, שניתן לפתור כל אחת בקלות, ולשלב חזרה למציאת הפתרון השלם.

עצרת, רקורסיה ו-call stack

עצרת היא מכפלת כל המספרים ממספר נתון ומטה עד ל-1. מסמנים עצרת בסימן קריאה! לדוגמה, עצרת של 3 היא:

3! = 3 * 2 * 1 = 6

האתגר הוא לכתוב קוד של פונקציה רקורסיבית לחישוב עצרת.

נקרא לפונקציה לחישוב עצרת fact (קיצור של factorial שזה עצרת באנגלית).

הפונקציה fact() מקבלת קלט n ומכפילה אותו בעצרת של `n-1`:

fact(n) = n * fact(n-1)

בשלב הבא של החישוב הקלט n יהיה `n-1`, ועבור השלב אחרי הבא הארגומנט n יהיה `n-2`, וחוזר חלילה, n קטן ב-1 בכל שלב. הבעיה היא שמחשב שמקבל כזו פונקציה ירוץ עד מינוס אינסוף או עד להצפת הזיכרון. הפתרון הוא להגדיר מקרה בסיס שבו הפונקציה תעצור. במקרה שלנו, מקרה הבסיס הוא 1, ובמקרה זה הפונקציה פשוט תחזיר 1 ותסיים את הקריאות הרקורסיביות:

# Recursive case
fact(n) = n * fact(n-1)

# Base case
fact(1) = 1

אחרי שהגדרנו את המקרה הרקורסיבי ואת מקרה הבסיס אנחנו יכולים לכתוב את הפונקציה:

def fact(n):
    # Base case
    if n == 1:
        return 1
    else:
        # Recursive case
        return n * fact(n-1)

• הקלט שמקבלת הפונקציה fact() הוא מספר שלם גדול מ-0 לו קראנו n.
• אם הקלט הוא 1 הפונקציה מחזירה 1.
• אחרת, הפונקציה מחזירה מכפלה של n במה שמחזירה הפונקציה כשהיא מקבלת את הקלט n-1.

כדי להחזיר את התשובה למהו `fact(3)` הפונקציה קודם כל צריכה להחזיר את התשובה למהו `fact(2)`, וכדי להחזיר את התשובה למהו `fact(2)` הפונקציה קודם כל צריכה להחזיר את התשובה למהו `fact(1)`. הארגומנט `n` מוגדר בתחילת התהליך כ-3, ובשלב הבא כ-2 ואז כ-1. כלומר, הערך של הקלט `n` משתנה בכל פעם שהפונקציה קוראת לעצמה. המסקנה היא ש-`n` שונה בין בכל פעם שהפונקציה קוראת לעצמה, והדרך לנהל את הקריאות לפונקציה ואת הערכים של `n` היא באמצעות call stack, מחסנית קריאות.

מהו call stack? ברוב שפות התכנות, כולל פייתון, כל קריאה לפונקציה נוספת למבנה נתונים הנקרא call stack מחסנית קריאות. כאשר פונקציה נקראת באופן רקורסיבי, פריט חדש מתווסף למחסנית, וכאשר הפונקציה חוזרת, הפריט מוסר. זה מאפשר לתוכנית לעקוב אחר מיקומה בתהליך הרקורסיבי.

הדרך הכי טובה להבין איך הרקורסיה מיושמת באמצעות call stack עובד היא באמצעות הרצת הפונקציה לעיל עם debugger. פה אני ממחיש את מה שראיתי בדיבאגר באמצעות איורים.

נקרא לפונקציה fact() עם הקלט 3:

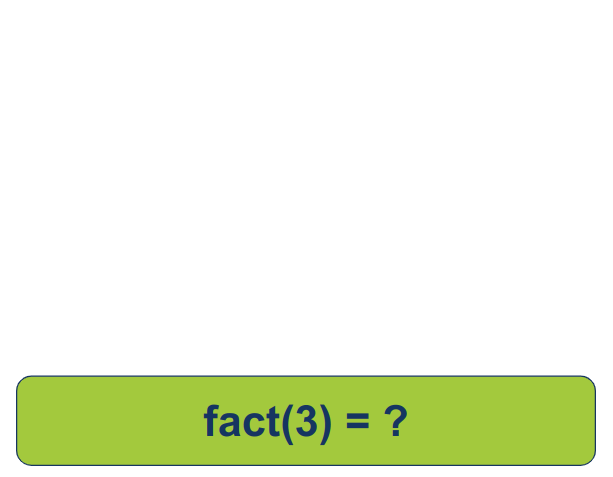
בשביל שהפונקציה fact() תוכל לענות על השאלה מהי עצרת של 3 היא צריכה לקרוא לעצמה עבור עצרת 2:

בשביל שהפונקציה fact() תוכל לענות על השאלה מהי עצרת של 2 היא צריכה לקרוא לעצמה עבור עצרת 1:

עצרת של 1 היא 1:

ולכן, הפונקציה תחזיר 1 ל-fact(2):

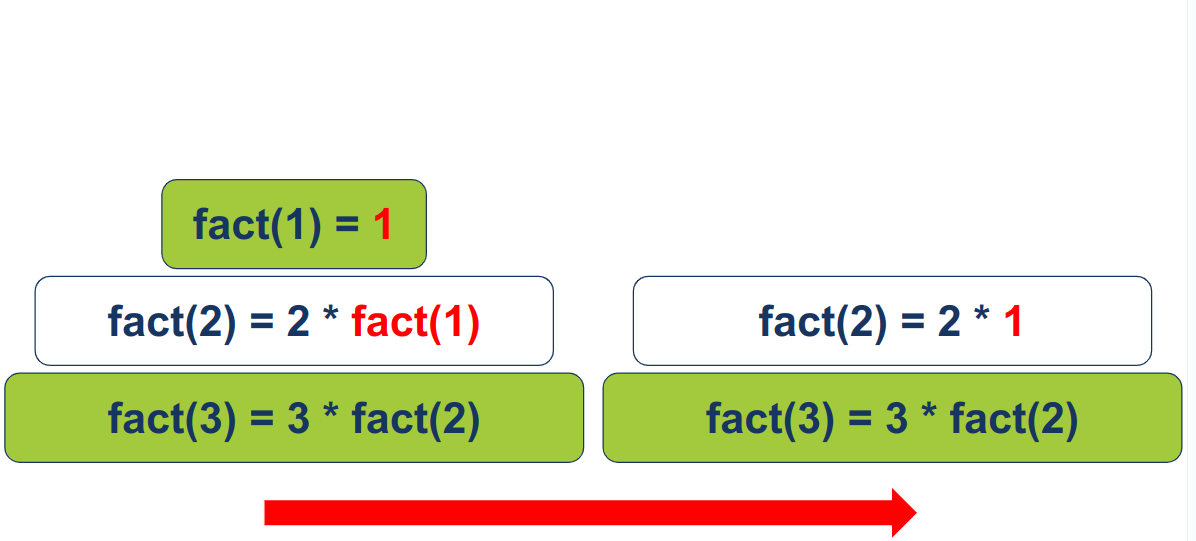
fact(2) תכפיל את מה שהיא מקבלת ב-2, והתוצאה היא 2:

הפונקציה תחזיר 2 ל-fact(3):

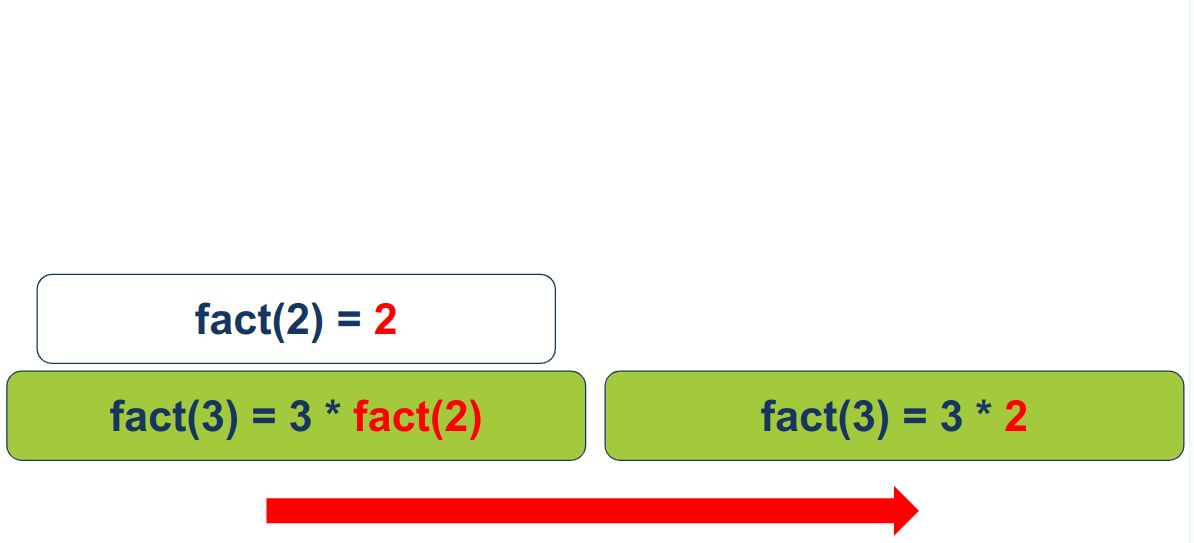
fact(3) תכפיל את מה שהיא מקבלת ב-3:

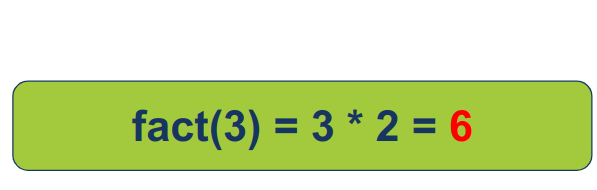
לבסוף, הפונקציה תחזיר 6.

בכל שלב הפונקציה קוראת לעצמה עבור ערך קטן ב-1 של `n`, ולאחר שהפונקציה נתקלת במקרה הבסיס (n=1) היא מחזירה 1 לפונקציה הקוראת, מה שמאפשר לפונקציה הקוראת לפתור את התרגיל עבור המקרה המסויים של `n`, ולהחזיר תשובה לפונקציה הקוראת, וחוזר חלילה, עד שלבסוף הפונקציה מחזירה את התשובה.

סדרת פיבונאצ'י

סדרת פיבונאצ'י היא רצף של מספרים שבו כל מספר שווה לסכום שתי הספרות הקודמות. המספרים הראשונים בסדרה הם:

Fibonacci Sequence = 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

• הפריט הראשון בסדרה הוא 0, והשני 1.
• הפריט השלישי הוא סכום הפריטים הראשון והשני 0 + 1 = 1
• הפריט הרביעי הוא סכום הפריטים השני והשלישי 1 + 1 = 2
• …
• הפריט העשירי הוא סכום הפריטים השמיני והתשיעי 21 + 13 = 34

וחוזר חלילה, כאשר הכלל הוא:

fib(0) = 0
fib(1) = 1
if n >=2 :
    fib(n) = fib(n - 1) + fib(n - 2)

התמונה הבאה מציגה חישוב של מספרי פיבונאצ'י עד למקום העשירי:

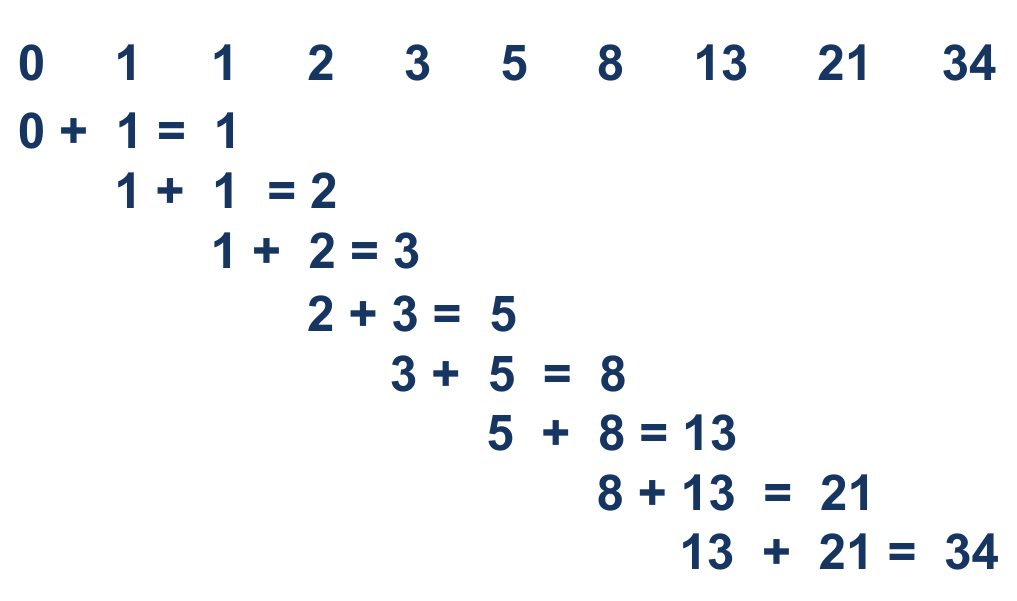
האתגר הוא לכתוב פונקציה שתחשב את ספרת פיבונאצ'י במקום ה-nי של הסדרה.

אנחנו יכולים לעבוד לפי הכלל לעיל. עבור n הקטן מ-2 נחזיר את n. זה מקרה הבסיס. ועבור יתר המקרים הפונקציה תקרא לעצמה עבור שתי הספרות הקודמות בסדרה. זה המקרה הרקורסיבי. נכתוב את זה:

def fib(n):    
    # Base cases
    if n < 2:
        return n
    # Recursive case
    else:
        return fib(n-1) + fib(n-2)

האיור הבא ממחיש את אופן עבודת הפונקציה באמצעות מבנה דמוי עץ:

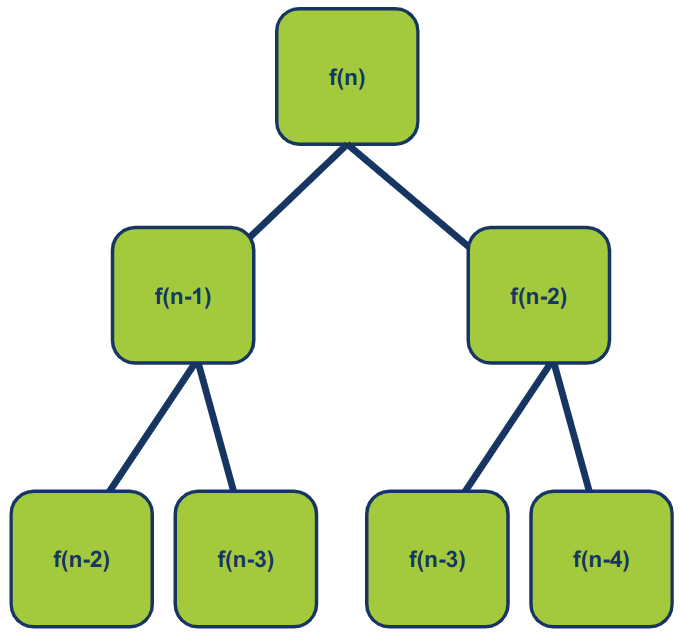
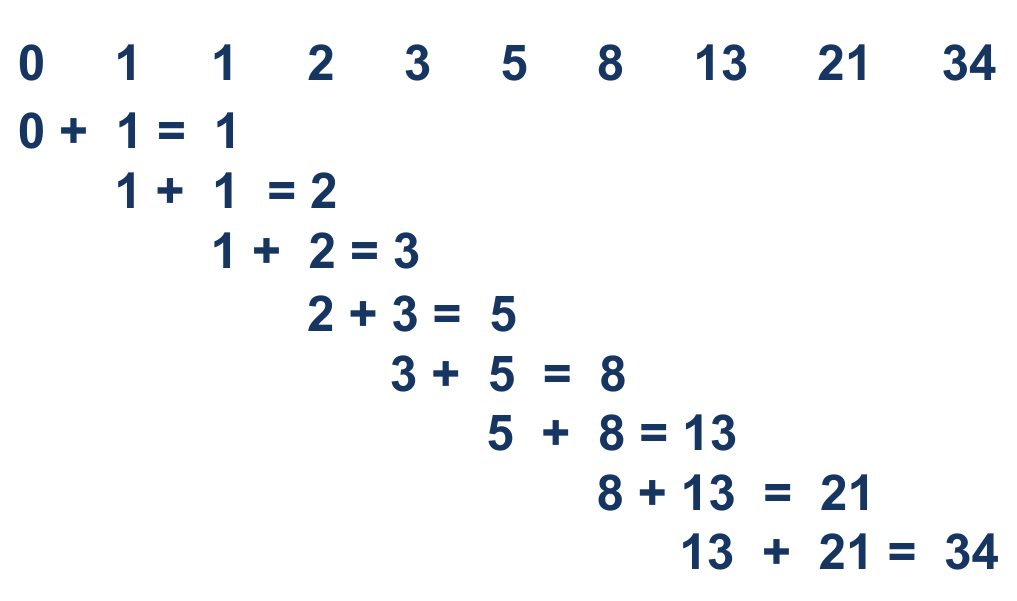
הפונקציה לא מיועדת לעבוד על מספרים שליליים אז נוסיף תנאי שעבור קלט של מספר שלילי הפונקציה תזרוק exception:

def fib(n):
    if n < 0:
        raise ValueError
("To calculate Fibonacci nth place please provide a non negative value")
    
    # Base cases
    if n < 2:
        return n
    # Recursive case
    else:
        return fib(n-1) + fib(n-2)

נבדוק את הפונקציה fib() לחישוב האיבר ה-nי של סדרת פיבונאצ'י:

print(fib(0)) # 0
print(fib(1)) # 1
print(fib(3)) # 2
print(fib(9)) # 34

רקורסיה - מקרי שימוש, יתרונות וחסרונות

רקורסיה היא טכניקה מאוד מקובלת בתכנות. להלן כמה סיבות להשתמש בה ומקרי שימוש נפוצים:

• טכניקת הפרד ומשול: רקורסיה מתאימה לבעיות שניתן לחלק לתת-בעיות קטנות וקלות לפתרון הדומות אחת לשנייה. אלגוריתמים כמו Merge Sort ו-Quick Sort משתמשים ברקורסיה כדי למיין מערכים בצורה יעילה, ואלגוריתמים כמו חיפוש בינארי משתמשים ברקורסיה כדי לחפש פריטים ברשימות ממוינות.
• מבנים דמויי עצים: בעיות הכוללות מבנים דמויי עצים, כגון עצים בינאריים, ניתן לעיתים קרובות לפתור בצורה אלגנטית באמצעות רקורסיה. מעבר traversal ושינוי עצים, מציאת נתיבים וביצוע חיפושים.
• מעבר traversal על גרפים ומניפולציה: בדומה לעצים, ניתן לייצג בקלות את המבנה של גרף כסדרה של תת-בעיות קטנות יותר. לדוגמה, ניתן להשתמש בפונקציה רקורסיבית כדי למצוא את כל המסלולים בין שני צמתים בגרף בגישה של BFS או DFS.
• Backtracking: אלגוריתמים רקורסיביים משמשים לעתים קרובות בבעיות backtracking, שבהן אתה חוקר אפשרויות שונות וחוזר אחורה כאשר אתה נתקל בנתיב ללא מוצא. דוגמאות קלאסיות כוללות פתרון פאזלים כמו סודוקו ובעיית ה-N-Queens, כמו גם יצירת קומבינציות ופרמוטציות.
• בעיות מתמטיות: רקורסיה משמשת לעתים קרובות לפתרון בעיות מתמטיות שיש להן הגדרות רקורסיביות. לדוגמה, חישוב המספרים של פיבונאצ'י, עצרת, ובעיית מגדל האנוי הם כולם רקורסיביים באופן טבעי.
• פישוט לוגיקה מורכבת: רקורסיה יכולה להפוך את הקוד שלך לאלגנטי יותר על ידי טריוויאליזציה של לוגיקה מורכבת בתוך פונקציה. היא יכולה להוביל לקוד נקי וקל יותר לקריאה, במיוחד כאשר מתמודדים עם דפוסים חוזרים.

מבני נתונים דינמיים: מבני נתונים רקורסיביים, כגון רשימות מקושרות ועצים, ניתנים לניהול בצורה אינטואיטיבית יותר באמצעות אלגוריתמים רקורסיביים. לדוגמה, אתה יכול לעבור traverse על רשימה מקושרת או מבנה עץ באופן רקורסיבי, מה שהופך את הקוד לקריא יותר.

אומנם רקורסיה היא טכניקה מאוד שימושית אבל יש להשתמש בה בזהירות בשל בעיות הנובעות משימוש בה:

• הצפה של מחסנית הקריאות stack overflow: רקורסיה מסתמכת על מחסנית הקריאות call stack, ורקורסיה עמוקה או בלתי מוגבלת עלולה להוביל לשגיאת הצפה של מחסנית הקריאות, שתביא לקריסה של התוכנית. ניתן לצמצם את הסיכון לכך על ידי הגבלת עומק הרקורסיה.
• בעיית ביצועים: פונקציות רקורסיביות יכולות להיות פחות יעילות ממקביליהם המשתמשים בלולאה עקב העומס של קריאות פונקציה וניהול הזיכרון call stack. הכנסת תוצאות הביניים לקאש או שימוש בלולאות עשוי לפתור הרבה בעיות, ותיכף נראה את זה.
• בעיה לקרוא את הקוד: רקורסיה יכולה לפעמים להקשות על מתכנתים לקרוא את הקוד, במיוחד אם היא כרוכה במספר רב של קריאות רקורסיביות או בתנאי בסיס מורכבים. כדי לפתור את הבעיה צריך לשים לב כשכותבים פונקציה רקורסיבית שמקרי הבסיס והמקרה הרקורסיבי מוגדרים היטב.

לסיכום, רקורסיה היא כלי תכנותי חשוב ביותר, במיוחד לפתרון בעיות בעלות מבנה רקורסיבי טבעי. עם זאת, חשוב לאזן את היתרונות שלה עם ההיבטים השליליים, ולשקול גישות חלופיות כאשר הן יעילות יותר או מתאימות יותר למשימה שעל הפרק.

Memoization - הכנסת תוצאות הביניים לקאש במטרה לייעל פונקציה רקורסיבית

Memoization היא טכניקה בה ניתן להשתמש כדי לייעל את החישוב של פתרונות לתת-בעיות על ידי אחסון בזכרון קאש של תוצאות שחושבו בעבר במטרה למנוע חישובים חוזרים ונשנים מה שמשפר משמעותית את היעילות של אלגוריתמים רקורסיביים.

Memoization כרוך בשימוש במבנה נתונים (כגון מילון או מערך) לאחסון תוצאות מחושבות עבור קלטים ספציפיים. לפני ביצוע קריאה רקורסיבית, האלגוריתם בודק האם התוצאה עבור קלט זה כבר מאוחסנת. אם כן, התוצאה המאוחסנת מוחזרת; אחרת, החישוב מבוצע, והתוצאה מאוחסנת לצורך שימוש בעתיד.

ראינו כבר כיצד להשתמש ברקורסיה לצורך חישוב סדרת פיבונאצ'י. במהלך החישוב ישנם חישובים החוזרים על עצמם:

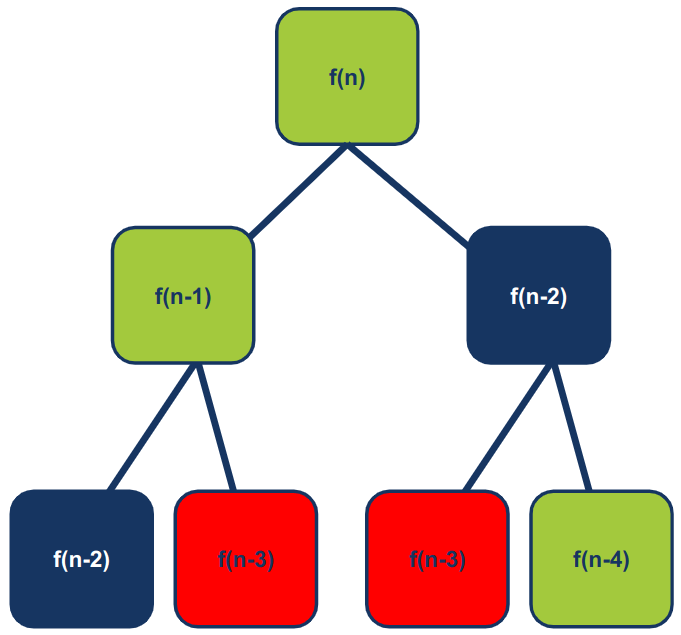
הקוד להלן משתמש ב-memoization לייעול פונקציה רקורסיבית המחשבת מספרי פיבונאצ'י:

def fib(n, memo={}):
  if n in memo:
    return memo[n]
  if n < 2:
    return n
  else:
    memo[n] = fib(n - 1, memo) + fib(n - 2, memo)
    return memo[n]

# test case
print(fib(10)) # 55

הפונקציה fib() מקבלת מספר טבעי כקלט ומחזירה את האיבר ה-n בסדרת פיבונאצ'י. הפונקציה משתמשת במילון memo כדי לאחסן תוצאות מחושבות עבור קלטים ספציפיים. לפני ביצוע קריאה רקורסיבית, הפונקציה בודקת האם התוצאה עבור קלט זה כבר מאוחסנת במילון. אם כן, התוצאה המאוחסנת מוחזרת; אחרת, החישוב מבוצע והתוצאה מאוחסנת במילון לצורך שימוש בעתיד.

נבחן את זמן הריצה של הפונקציה למציאת מספר פיבונאצ'י במקום ה-40 ללא memoization:

import time


start = time.time()


def fib(n):
    if n < 2:
        return n
    else:
        return fib(n-1) + fib(n-2)
        
print(fib(40)) # 102334155


end = time.time()
print(f"Time elapsed {end - start} seconds")

• כשהרצתי את הפונקציה למציאת מספר פיבונאצ'י במקום ה-40 משך הריצה היה כמעט 13 שניות.

נוסיף לפונקציה memoization בצורת מילון שיאחסן את הערכים המחושבים ואפשר יהיה למשוך אותם ממנו בהמשך:

# Dictionary to store cached Fibonacci values
memo = {}
def fib(n):
    # Check if the value is already in the cache
    if n in memo:
        return memo[n]
    
    if n < 2:
        return n
    else:
        # Recursive case with memoization
        result = fib(n-1) + fib(n-2)
        
    # Cache the result before returning
    memo[n] = result
    return result

• משך הריצה היה 32 מיליונית השנייה עם קאש. מה שאומר שיפור של פי מיליונים במהירות הריצה. פשש…

לולאה במקום רקורסיה

רקורסיה ושימוש בלולאה (=איטרציה) הן שתי טכניקות משלימות לפתרון בעיות, וברוב המקרים, בעיה שניתן לפתור באופן רקורסיבי ניתן לפתור גם באופן איטרטיבי.

ראינו איך לחשב עצרת באמצעות רקורסיה, עכשיו נעשה את אותו הדבר באמצעות לולאה:

def factorial(n): 
    for i in range(1, n + 1): 
        result *= i 
    return result 

• אנו משתמשים בלולאת for כדי לעבור על המספרים מ-1 עד n ולהכפיל את התוצאה בכל שלב במספר התורן. הלולאה צוברת את מכפלת המספרים, וכך מחשבת את העצרת.

קיימים מספר תרחישים בהם השימוש באיטרציה עדיף על רקורסיה:

• יעילות: איטרציה היא לעתים קרובות יעילה יותר מרקורסיה מבחינת סיבוכיות זמן ומקום. קריאות פונקציות רקורסיביות עלולות להוביל למספר קריאות גבוה לפונקציה, מה שעלול לגרום להצפת הזיכרון stack overflow. איטרציה בדרך כלל משתמשת בפחות זיכרון והיא מהירה יותר מכיוון שהיא לא כוללת את העומס של קריאות לפונקציה.
• פשטות כתיבה והבנה: לחלק מהבעיות פתרון מבוסס לולאה הוא אינטואיטיבי וקל להבנה יותר מאשר פתרונות רקורסיביים. לדוגמה, פעולות מתמטיות פשוטות, מניפולציות של מערכים ותהליכים סדרתיים.
• תהליכים סדרתיים: בעת פתרון בעיות הכרוכות בעיבוד סדרתי, כגון קריאת קובץ שורה אחר שורה או מעבר על רשימה מקושרת, איטרציה היא הבחירה הטבעית מכיוון שהיא עוקבת אחר הטבע הסדרתי של הבעיה.
• ניפוי שגיאות קל יותר: כשכותבים קוד איטרטיבי קל יותר לזהות ולטפל בשגיאות, במיוחד עבור בעיות מורכבות, מכיוון שהלולאה מאופיינת בבקרת זרימה לינארית שקל יותר לעקוב אחרי התפתחותה.

חשוב לציין שרקורסיה יכולה להיות גישה אלגנטית וטבעית יותר עבור חלק מהבעיות, במיוחד אם הן מבוססות על מבנה רקורסיבי, כגון מעבר על עץ או גרף, ובעיות שפותרים בגישה של הפרד ומשול. בסופו של דבר, הבחירה בין רקורסיה לאיטרציה תלויה בבעיה שעל הפרק.

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

אלגוריתמים כדוגמת Merge Sort ו-Quick Sort משתמשים ברקורסיה כדי למיין מערכים ביעילות.

אלגוריתם כמו חיפוש בינארי משתמשים ברקורסיה לחיפוש פריטים ברשימות ממוינות.

בעיות הכוללות מבנים דמויי עצים, כגון עצים בינאריים, ניתן לעיתים קרובות לפתור בצורה אלגנטית באמצעות רקורסיה. מעבר traversal ושינוי עצים, מציאת נתיבים וביצוע חיפושים.

ניתן להשתמש בפונקציה רקורסיבית כדי למצוא את כל המסלולים בין שני צמתים בגרף בגישה של BFS או DFS.

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים