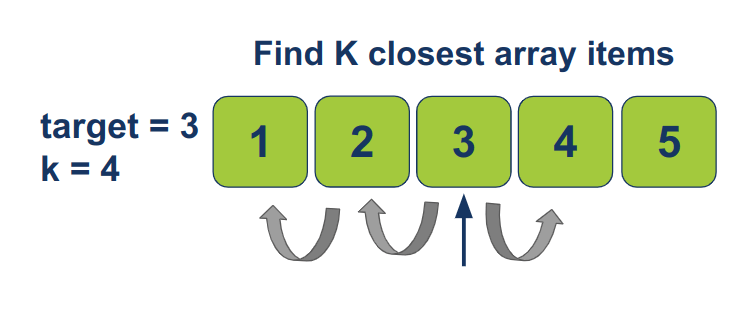
חידה תכנותית: מציאת הפריטים הקרובים ביותר לערך מטרה בתוך מערך

נתון לך מערך `arr` של מספרים שלמים ממוינים בסדר עולה מהפריט הנמוך לגבוה, וערך מטרה `target`. עליך למצוא את k הפריטים הקרובים ביותר לערך המטרה במערך. במקרה של שוויון יש להעדיף את הפריט הקטן יותר:

If abs(target - arr[lo]) <= abs(target - arr[hi])
    Take arr[lo]

לשם כך עליך לכתוב פונקציה find_k_closest():

def find_k_closest(arr: List[int], target: int, k: int) -> List[int]:
    pass

קלט הפונקציה:

• `arr` - מערך מספרים שלמים ממוינים בסדר עולה
• `target` - ערך מטרה שהוא מספר שלם
• `k` - מספר הפריטים הקרובים ביותר שאותו יש למצוא

פלט הפונקציה:

רשימה של k מספרים שהם הפריטים הקרובים ביותר ליעד המטרה במערך. הרשימה המוחזרת צריכה להתמיין בסדר עולה.

לדוגמה:

Inputs:  arr = [1, 2, 3, 4, 5], target = 3, k = 2
Output: [2, 3]

התוצאה שצריכה להחזיר הפונקציה היא: 2 ו-3. כי 3 זהה לערך המטרה, ובין שתי האפשרויות 2 ו-4, שניהם נמצאים במרחקים שווים מ-3, נעדיף את 2 כי ההעדפה היא לערכים הנמוכים.

שים לב:

• ערך המטרה `target` לא חייב להיות במערך עם כי הוא יכול להיות.
• אם `target` קיים במערך הוא צריך להיות חלק מהמערך אותו הפונקציה מחזירה כתשובה.

דוגמאות:

assert find_k_closest([1, 2, 3, 4, 5], 3, 2) == [2, 3]
assert find_k_closest([12, 16, 22, 30, 35, 39, 42, 45, 48, 50, 53, 55, 56], 35, 4) == [30, 35, 39, 42]
assert find_k_closest([-1, 1, 3, 5, 7, 8, 9], 2, 3) == [-1, 1, 3]
assert find_k_closest([1, 3, 5, 7, 8, 9], 4, 3) == [1, 3, 5]
assert find_k_closest([1, 3, 5, 7, 8], 6, 3) == [5, 7, 8]
assert find_k_closest([10, 20, 30, 40, 50], 35, 2) == [30, 40]

הצעה לפתרון

הרעיון הוא להשתמש בחיפוש בינארי בשביל למצוא את ערך המטרה `target`. אפילו אם לא נמצא את ערך המטרה עדיין נמצא את הערכים הסמוכים ל-`target`. אחרי שנמצא ביעילות את הסביבה של המטרה במערך, נוכל לחפש בה את k הערכים הסמוכים באמצעות טכניקת שני המצביעים.

הצעת קריאה:

• אלגוריתם חיפוש בינארי - מהבנה ליישום

• שימוש בטכניקת שני המצביעים לפתרון בעיות תכנותיות

השלב הראשון של הפתרון הוא וריאציה של חיפוש בינארי שמאפשר לנו למצוא את המטרה ביעילות, במורכבות זמן log(N):

def find_k_closest(arr, target, k):
    lo = 0
    hi = len_arr - 1
    while lo <= hi:
        mid = (lo + hi) // 2
        if arr[mid] <= target:
            lo = mid + 1
        else:
            hi = mid - 1

• את החיפוש הבינארי עושים רק בתוך מערך מסודר. נניח שהמערך מסודר בסדר מספרים עולה (אם זה לא ברור בבקשה לקרוא את המדריך על חיפוש בינארי).
• שני המצביעים `lo` ו-`hi` מתעדכנים בתוך לולאה שרצה כל עוד המצביע `lo` מצביע על פריט מערך שערכו נמוך מ-`hi`.
• בתוך הלולאה מחושב `mid` הממוצע (מעוגל כלפי מטה) של האינדקסים שעליהם מצביעים `lo` ו-`hi`. `mid` חוצה את המערך ומאפשר לשאול באיזה חצי נמצא ערך המטרה: בחצי שמכיל את הערכים הגבוהים מהערך עליו מצביע `mid` או בחצי המצביע על הערכים הנמוכים ממנו; החצי הגבוה או הנמוך.
• אם הערך שנמצא באינדקס `mid` הוא נמוך מערך המטרה `target` אז המטרה נמצאת בחצי שמעל ל-`mid` לפיכך נעדכן את ערך המצביע `lo` שיהיה `mid+1` מה שיגרום להמשך החיפוש בחצי הגבוה.
• להבדיל, אם הערך שנמצא באינדקס `mid` הוא גבוה מערך המטרה `target` אז המטרה נמצאת בחצי שמתחת ל-`mid` לפיכך נעדכן את ערך המצביע `hi` שיהיה `mid-1` מה שיגרום להמשך החיפוש בחצי הנמוך.

החיפוש הבינארי שימש אותנו לצמצם את החיפוש.

בחלק השני של הפתרון נשתמש באותם שני המצביעים בהם השתמשנו לצורך החיפוש הבינארי הפעם במטרה להרחיב את החיפוש עד שנמצא k פריטים הקרובים ביותר למטרה. הגישה בה נשתמש היא טכניקת שני המצביעים:

# Initialize a deque for efficient appending from both ends
result = deque()
  
# Swap the pointers since the left pointer (`lo`)
# is to the right of the right pointer (`hi`)
# when exiting the binary search
lo, hi = hi, lo
  
# Continue iterating until finding the required
# number of closest elements
while k > 0:
    if lo < 0:
        # No elements on the lower side,
        # so take elements from the higher side
        result.append(arr[hi])
        hi += 1
    elif hi > len_arr - 1:
        # No elements on the higher side,
        # so take elements from the lower side
        result.appendleft(arr[lo])
        lo -= 1
    elif abs(target - arr[lo]) <= abs(target - arr[hi]):
        # If the element to the left is closer to the target,
        # add the element to the lower side of the results array
        # and continue exploring the lower side
        result.appendleft(arr[lo])
        lo -= 1
    else:
        # If the element to the right is closer to the target,
        # add the element to the higher side of the results array
        # and continue exploring the higher side
        result.append(arr[hi])
        hi += 1
    k -= 1

• משתמשים ב-deque במקום במערך בשביל לאסוף את הפריטים שיהוו את התשובה בגלל שההכנסה לשני הצדדים נעשית בסיבוכיות זמן קבועה O(1).
• מחליפים את מיקום האינדקסים של המצביעים `lo` ו-`hi` בגלל שביציאה מהחיפוש הבינארי הערך עליו מצביע `lo` הוא נמוך יותר מהערך עליו מצביע `hi` אז מחליפים ביניהם כדי להחזיר את הסדר הנכון.
• את החיפוש עושים בתוך לולאה while שרצה כל עוד k גדול מ-0 כיוון שאנחנו רוצים למלא את ה-deque ב-k פריטי מערך.

• בתוך הלולאה מבחינים בין 3 מצבים:

  1. אם המצביע `lo` מצביע על ערך אינדקס נמוך מ-0 אין יותר פריטים נמוכים מערך המטרה שניתן לשלב בפתרון ולכן נשלב את הערך עליו מצביע `hi`, וגם נקדם את `hi` מקום ימינה כדי שבריצה הבאה של הלולאה תהיה אפשרות לשלב את הערך הבא של המערך הגבוה יותר או שווה בערכו.
  2. אם המצביע `hi` מצביע על ערך אינדקס הגדול מאורך המערך אז אין יותר פריטים בעלי ערך גבוה מערך המטרה שניתן לשלב בפתרון ולכן נשלב את הערך עליו מצביע `lo`, ואף נסיג את `lo` מקום אחד לשמאל כדי שבריצה הבאה של הלולאה תהיה אפשרות לשלב את הערך הבא הנמוך יותר או שווה בערכו של המערך.
  3. אם שני המצביעים `lo` ו-`hi` נמצאים בתוך גבולות המערך אז צריך להשוות בין ערך הפריט עליו מצביע `lo` לבין ערך הפריט עליו מצביע `hi`. אם הערך עליו מצביע `lo` הוא סמוך יותר לערך המטרה `target` אז נשלב אותו אחרת נשלב את הערך עליו מצביע `hi`.

ביציאה מהלולאה ה-deque מתמלא ב-k פריטים. הפונקציה תהפוך את ה-deque,ותחזיר את הרשימה.

הקוד המלא של הפונקציה למציאת k פריטים הסמוכים לערך המטרה:

from collections import deque


def find_k_closest(arr, target, k):
   len_arr = len(arr)
   # Handle the edge case where the array
   # has fewer elements than required
   if len_arr <= k:
       return arr
  
   # Binary search to get to the proximity of the target
   # efficiently in logarithmic time complexity
   lo = 0
   hi = len_arr - 1
   while lo <= hi:
       mid = (lo + hi) // 2
       # Skip the exact match to avoid interference with the results
       # if arr[mid] == target:
       if arr[mid] <= target:
           lo = mid + 1
       else:
           hi = mid - 1
          
   # Initialize a deque for efficient appending from both ends
   result = deque()
  
   # Swap the pointers since the left pointer (`lo`)
   # is to the right of the right pointer (`hi`)
   # when exiting the binary search
   lo, hi = hi, lo
  
   # Continue iterating until finding the required
   # number of closest elements
   while k > 0:
       if lo < 0:
           # No elements on the lower side,
           # so take elements from the higher side
           result.append(arr[hi])
           hi += 1
       elif hi > len_arr - 1:
           # No elements on the higher side,
           # so take elements from the lower side
           result.appendleft(arr[lo])
           lo -= 1
       elif abs(target - arr[lo]) <= abs(target - arr[hi]):
           # If the element to the left is closer to the target,
           # add the element to the lower side of the results array
           # and continue exploring the lower side
           result.appendleft(arr[lo])
           lo -= 1
       else:
           # If the element to the right is closer to the target,
           # add the element to the higher side of the results array
           # and continue exploring the higher side
           result.append(arr[hi])
           hi += 1
       k -= 1


   return list(result)

כמה מקרי בדיקה:

# Test cases


# Target is in the array
print(find_k_closest([1, 2, 3, 4, 5], 3, 3))          # Output: [2, 3, 4]
# Target is not in the array
print(find_k_closest([1, 2, 4, 5], 3, 3))             # Output: [1, 2, 4]
# Target is on the left side of the array
print(find_k_closest([1, 2, 3, 4, 5], 1, 2))          # Output: [1, 2]
# Target is on the right side of the array
print(find_k_closest([1, 2, 3, 4, 5], 5, 3))          # Output: [3, 4, 5]
print(find_k_closest([12, 16, 22, 30, 35, 39, 42, 45, 48, 50, 53, 55, 56], 35, 4)) # Output: [30, 35, 39, 42]
print(find_k_closest([-1, 1, 3, 5, 7, 8, 9], 2, 3))   # Output: [-1, 1, 3]
print(find_k_closest([1, 3, 5, 7, 8, 9], 4, 3))       # Output: [1, 3, 5]
print(find_k_closest([1, 3, 5, 7, 8], 6, 3))          # Output: [5, 7, 8]
# target is lower than the lowest element
print(find_k_closest([1, 2, 3, 4, 5], 0, 2))          # Output: [1, 2]
# target is higher than the highest element
print(find_k_closest([1, 2, 3, 4, 5], 6, 2))          # Output: [4, 5]
print(find_k_closest([10, 20, 30, 40, 50], 35, 2))    # Output: [30, 40]
print(find_k_closest([10, 20, 30, 40, 50], 0, 2))     # Output: [10, 20]

הערכת ביצועים

הפונקציה מורכבת משני חלקים עיקריים:

חלק ראשון, חיפוש בינארי, בעל סיבוכיות זמן של O(log N). בכל פעם שהלולאה רצה, החיפוש מצמצם את מרחב החיפוש בחצי.

חלק שני, טכניקת שני המצביעים (two-pointer approach), המורכבת מ-O(k) צעדים. בגישה זו עוברים על k איברים במסגרת חיפוש לינארי.

לסיבוכיות הזמן הכוללת תורמים שני החלקים, זה של החיפוש הבינארי וזה של טכניקת שני המצביעים, ששילובם מביא לסיבוכיות זמן כוללת של O(log N + k). עם זאת, ככל שהמערך מתארך גדלה תרומתו של החיפוש הבינארי, מה שמביא לסיבוכיות זמן כוללת של O(log N) עבור מערכים ארוכים עקב הזנחת תרומת החיפש הלינארי.

סיבוכיות המקום היא O(k) מכיוון שה-deque תופס k יחידות זיכרון.

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

אלגוריתם חיפוש בינארי - מהבנה ליישום

שימוש בטכניקת שני המצביעים לפתרון בעיות תכנותיות

טכניקת חלון ההזזה sliding window לפתרון בעיות ברצפים

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים