פתרון בעיית הקיטבג knapsack באמצעות תכנות דינמי

בעיית הקיטבג knapsack מופיעה בוריאציות שונות בפרדיגמות שונות של תכנות. במדריך זה נלמד לפתור אותה באמצעות רקורסיה ותכנות דינמי dynamic programming.

הגרסה שאני מכיר של בעיית הקיטבג מספרת על גנב שפורץ לחנות מחשבים ועכשיו הוא צריך למלא את השק שלו בכמה שיותר פריטים. אם הוא יתמהמה יותר מדי המשטרה תתפוס אותו. לכן הוא צריך לחשוב מהר. הבעיה היא שהשק מוגבל מבחינת משקל החפצים שהוא יכול לשאת אז כדאי לו לקחת חפצים כמה שיותר יקרים אחרת הוא מסתכן לחינם.

קיבולת השק (=המשקל המקסימלי שהוא יכול לשאת) הוא 6 ק"ג, והוא יכול לבחור בין 4 פריטים:

משקל הפריטים הכולל הוא 10 ק"ג בעוד קיבולת השק היא רק 6 ק"ג לכן הוא לא יוכל לגנוב את כל הפריטים.

הגנב לא יכול לחצות פריט ורשאי לקחת לכל היותר פריט אחד לכן השם המלא של הבעיה הוא 0/1 knapsack problem. לוקח או לא לוקח, ואם לוקח אז רק אחד.

כמה שילובי פריטים יש לנו?

אפשר לקחת את כל הפריטים : [1, 2, 3, 4]

או רק את 3 הפריטים הראשונים: [1, 2, 3]

או פריט ראשון ואחרון בלבד: [1, 4]

או לא לקחת אף פריט : []

לא כל הקומבינציות נותנות תוצאה מקסימלית או אפשריות מבחינת זה שהשק מוגבל במשקל שהוא יכול לשאת אבל אם מסתכלים רק על מספר הקומבינציות מגלים שאפילו שיש רק ארבעה פריטים ניתן לקבל לא מעט שילובים. כמה? מכיוון שיש לנו 4 פריטים ועבור כל אחד מהם אפשר לבחור בין 2 אפשרויות, להכניס לשק או לוותר, הקומבינטוריקה מלמדת שמספר האפשרויות הוא :

2^4 = 16

האפשרות הפשוטה ביותר היא לבחון את כל הקומבינציות של הפריטים ולמצוא מתוכם את הקומבינציה שנותנת את הרווח הגבוה ביותר ב-$ ובתנאי שלא עוברים את המכסה שהשק יכול להכיל בתוכו.

מה זה אומר לבחון קומבינציה? זה אומר לעבור על כל פריט מהפריטים ולבדוק האם אנחנו יכולים להכניס לשק וגם האם כדאי להכניס לשק.

את תהליך הבחינה של כל קומבינציה בנפרד אנחנו עושים 16 פעמים.

כשאנחנו רוצים לעשות את אותם פעולות שוב ושוב אנחנו יכולים לבחור בין 2 גישות: איטרטיבית באמצעות לולאה או רקורסיבית כאשר פונקציה קוראת לעצמה שוב ושוב עד שהיא מפסיקה.

במקרה זה, נבחר בפתרון רקורסיבי. פונקציה קוראת לעצמה שוב ושוב עד שהיא מפסיקה מכיוון שהיא נתקלת במקרה בסיס - תנאי שלא מאפשר לה להמשיך. מקרה הבסיס הוא שאין יותר פריטים שאותם ניתן לבחון או שקיבולת השק אינה מאפשרת הכנסת פריט נוסף.

# base case
if current_capacity == 0 or current_item == 0:
    return 0

המקרה הרקורסיבי הוא שהפונקציה קוראת לעצמה. נגדיר את הפונקציה:

def recur_knapsack(weights=[], values=[], current_capacity=0, current_item=0):
    # base case
    if current_capacity == 0 or current_item == 0:
        return 0

הפרמטרים הם:

• weights - רשימת המשקלים
• values - רשימת הערכים
• current_item - נתחיל מהפריט האחרון ועם הרקורסיה נוריד בכל פעם פריט אחד עד שנעצור כשנגיע למצב בו אין יותר פריטים (מקרה הבסיס).
• current_capacity - קיבולת השק. החלק של השק אותו עדיין נשאר למלא. מתחילים משק ריק וכל הוספה של פריט מפחיתה מקיבולת השק.

מתחילים מקיבולת שק מירבית, ובכל פעם שמכניסים פריט לשק הקיבולת פוחתת. לדוגמה, מתחילים מקיבולת של 6 ק"ג ואז מכניסים פריט במשקל 2 ק"ג אז קיבולת השק יורדת ל-4 ק"ג.

ההחלטה היא בינארית. 1 או 0. להכניס לשק או לא.

סיבה אחת לא להכניס פריט לשק היא בגלל שהמשקל שלו חורג מקיבולת השק :

weights[current_item] > current_capacity

אם אנחנו בוחרים להשאיר את הפריט בחוץ אז קיבולת השק נשארת כמו שהיא ועוברים לבחון את הפריט הבא על ידי קריאה רקורסיבית לפונקציה:

# in case the current item is heavier
# than the space left in the bag (=bag capacity)
if weights[current_item] > current_capacity:
    # exclude
    return recur_knapsack(weights, values, current_capacity, current_item-1)

• הקיבולת נשארת כמו שהיא כי לא הוספנו את הפריט לשק (current_capacity).
• קוראים לפונקציה עבור הפריט הקודם ברשימה (current_item-1).

במקרה בו משקל הפריט נמוך או שווה מהקיבולת שהשק עוד יכול להכיל הבחירה היא בין שתי אפשרויות: להוסיף את הפריט או להשאיר מחוץ לשק. מבין שתי האפשרויות נבחר בזו שנותנת את הערך הגבוה יותר.

# in case the current item is equal or less
# you have 2 choices exclude or include
# whatever makes the maximum profit
if weights[current_item] <= current_capacity:
       return max(item_exclusion, item_inclusion)

את הקוד עבור הבחירה להשאיר את הפריט מחוץ לשק ראינו לעיל:

item_exclusion = recur_knapsack(weights, values, current_capacity, current_item-1)

במידה ובוחרים להוסיף את הפריט לשק צריך להוסיף את הערך של הפריט הנוכחי לערכים הנצברים על ידי בחירה באופציה זו (איך מוצאים את הערכים הנצברים? קוראים לפונקציה באופן רקורסיבי):

# Get current item value in $
current_value = values[current_item]

# Update knapsack capacity with the weight of the current item
updated_capacity = current_capacity-weights[current_item]

# Add the current value to the accumulated values (obtained through the recursive process)
current_value+recur_knapsack(weights, values, updated_capacity, current_item-1)

כיוון שהוספנו את הפריט לשק קיבולת השק פוחתת בהתאם למשקל הפריט. הקיבולת העדכנית:

updated_capacity = current_capacity-weights[current_item]

נכתוב את הקוד המלא לפתרון רקורסיבי של בעיית הקיטבג:

def recur_knapsack(weights=[], values=[], current_capacity=0, current_item=0):
    # base case
    if current_capacity == 0 or current_item == 0:
        return 0
  
    # recursion
  
    # in case the current item is heavier
    # than the space left in the bag (=bag capacity)
    if weights[current_item] > current_capacity:
        # exclude
        return recur_knapsack(weights, values, current_capacity, current_item-1)
  
    # in case the current item is equal or less
    # you have 2 choices exclude or include
    # whatever makes the maximum profit
    if weights[current_item] <= current_capacity:
        # exclude
        item_exclusion = recur_knapsack(weights, values, current_capacity, current_item-1)
      
        # include
        current_value = values[current_item]
        updated_capacity = current_capacity-weights[current_item]
        item_inclusion = current_value + recur_knapsack(weights, values, updated_capacity, current_item-1)
        return max(item_exclusion,
                  item_inclusion)

נבחן את הפתרון:

weights = [4, 1, 2, 3]
values =  [4, 8, 1, 8]
max_weight = 6
res = recur_knapsack(weights, values, max_weight, len(values)-1)
print(res) # 17

מה קורה אם אחד הקלטים הוא מספר שלילי?

values =  [1, -4, 8, 5]
weights = [3, 3, 5, 6]
max_weight = 11
res = recur_knapsack(weights, values, max_weight, len(values)-1)
print(res) # 13

מה קורה כאשר ערכים ומשקלים חוזרים יותר מפעם אחת ברשימה?

values =  [2, 2, 4, 5, 3]
weights = [3, 1, 3, 4, 2]
max_weight = 12
res = recur_knapsack(weights, values, max_weight, len(values)-1)
print(res) # 14

מה קורה כאשר הקיבולת המקסימלית של השק היא 0?

values =  [1, 2]
weights = [2, 3]
max_weight = 0
res = recur_knapsack(weights, values, max_weight, len(values)-1)
print(res) # 0

בדיקה נוספת היא להעביר מערכים ריקים או בעלי אורך בלתי שווה אז מתקבלת שגיאה. אפשר לטפל בזה על ידי שימוש ב-Exception (קרא על Exception בפייתון).

במסגרת הגישה הרקורסיבית אנחנו צריכים לבחון את כל האפשרויות, ומספר האפשרויות תלוי בכמות הפריטים. לדוגמה, אם 2 פריטים שניתן לבחור בין להוסיף לשק או להשאיר בחוץ אז מספר האפשרויות על פי חוקי הקומבינטוריקה הוא:

2^2 = 4

אם 3 פריטים:

2^3 = 8

אם 4 פריטים:

2^4 = 16

כל פריט שנוסיף לקלט יכפיל את מספר הקומבינציות. בהתאם, אם נספק קלט של 10 פריטים אז נצטרך לבדוק יותר מ-1,000 צירופים. ואם 20 פריטים נהיה חייבים לבדוק יותר ממיליון קומבינציות.

אפשר לראות גידול אקספוננציאלי של כמות החישובים ביחס לכמות הקלטים. קצב גידול שאותו נסמן באמצעות הנוטציה של big-o:

O(2^N)

מה שאומר שהקוד לא יעיל. אם זה לא ברור אז כדאי לך לקרוא על "big-o ביטוי ליעילות קוד".

פתרון בעיית הקיטבג באמצעות תכנות דינמי dynamic programming

אחרי שלמדנו על פתרון בעיית הקיטבג באמצעות רקורסיה, והבנו מדוע הפתרון אינו יעיל, הגיע הזמן לנסות דרך שונה המסתמכת על תכנות דינמי dynamic programming וגורסת שלא צריך לבחון את כל הקומבינציות. במקום זה אנחנו מאחסנים את תוצאות החישובים, ואח"כ חוזרים אליהם במקום לחשב מחדש.

תכנות דינמי מבוסס על עבודתו של ריצ'רד בלמן במסגרתו נשבור בעיה גדולה לבעיות קטנות שאותם אפשר לפתור בקלות, את הפתרונות שומרים בזיכרון, ומשלבים אותם כדי למצוא את הפתרון לבעיה הגדולה.

קיימות שתי גישות לתכנות דינאמי:

• Top-down מלמעלה למטה 
• Bottom-up מלמטה למעלה

גישת Top-down משתמשת לרוב ברקורסיה. בשיטה הזו מזהים את הדפוס ואז מיישמים את הפתרון. גישת Top-down מכונה גם memoization.

גישת Bottom-up משתמשת בעיקר בלולאות. היא נחשבת ליותר יעילה. במסגרתה מבינים קודם כיצד לפתור את הבעיות הקטנות ומזה מסיקים כיצד לפתור את הבעיה הגדולה. גישת Bottom-up מכונה גם tabulation.

פתרון בעיית הקיטבג באמצעות Memoization

נחזור לבעיית הקיטבג. אנחנו יודעים לשבור את הבעיה הגדולה לבעיות קטנות באמצעות רקורסיה אבל אנחנו לא שומרים את תוצאות החישוב בשום מקום מה שגורם לזה שאנחנו צריכים לחזור על אותם החישובים במקום לקחת את התוצאות של החישובים שערכנו השמורים בזיכרון.

הרעיון של לשמור את תוצאות החישוב בזיכרון מכונה memoization (מלשון memo - פתק תזכורת שאנחנו כותבים לעצמנו).

אפשר לאחסן את הפתרונות במילון dictionary של פייתון שבו המפתחות (keys) יהיו המצבים: מספר פריט וקיבולת השק, והערך (value) יהיה תוצאת החישוב.

נקרא למילון שבו נשתמש בקוד MEMO:

MEMO = {}

תוצאות החישוב תלויות במספר הפריט ובקיבולת השק. בהתאם, המפתח יהיה סט המורכב משני פריטים:

(current_item, current_capacity)

הערך אותו נאחסן במילון יהיה תוצאת החישוב:

MEMO[(current_item, current_capacity)] = res  

נחזור לקוד הרקורסיבי והלא יעיל אותו פיתחנו בסעיף הקודם ונהפוך אותו לדינמי ויעיל הרבה יותר על ידי כך שבכל פעם שיש לנו תוצאה של חישוב נשמור אותה בזיכרון, ב-MEMO. כך שאם נתקל שוב באותו מצב בהמשך הדרך (שילוב של מספר פריט וקיבולת שק) ניקח את התוצאה מהזיכרון במקום לחשב מחדש.

נוסיף לפונקציה הרקורסיבית לעיל מילון שנקרא לו MEMO :

MEMO = {}
def memo_knapsack(weights=[], values=[], current_capacity=0, current_item=0):
    # The rest of the function

את מקרה הבסיס נשאיר כמו שהוא:

def memo_knapsack(weights=[], values=[], current_capacity=0, current_item=0):
   # base case
   if current_capacity == 0 or current_item == 0:
       return 0

אם קיים בזיכרון המצב העכשווי (שילוב של קיבולת שק ומספר פריט) אז צריך להחזיר את התוצאה שלו:

MEMO = {}
def memo_knapsack(weights=[], values=[], current_capacity=0, current_item=0, memo={}):
    # base case
    if current_capacity == 0 or current_item == 0:
        return 0
  
    # if current states in memo
    # return the value
    if (current_item, current_capacity) in MEMO:
        return MEMO[(current_item, current_capacity)]

אם המצב לא קיים בזיכרון אז צריך לחשב אותו, כמו שעשינו כבר בקוד הרקורסיבי לעיל. רק שהפעם נשמור את התוצאה בזכרון:

# recursion
  
# in case the current item is heavier
# than the space left in the bag (=bag capacity)
if weights[current_item] > current_capacity:
    # exclude
    res = recur_knapsack(weights, values, current_capacity, current_item-1)
   
# in case the current item is equal or less
# you have 2 choices exclude or include
# whatever makes the maximum profit
if weights[current_item] <= current_capacity:
    # exclude
    item_exclusion = recur_knapsack(weights, values, current_capacity, current_item-1)
      
    # include
    current_value = values[current_item]
    updated_capacity = current_capacity-weights[current_item]
    item_inclusion = current_value + recur_knapsack(weights, values, updated_capacity, current_item-1)
    res = max(item_exclusion, item_inclusion)
  
# store in memo
MEMO[(current_item, current_capacity)] = res

הפתרון המלא לבעיית הקיטבג מבוסס על memoization:

MEMO = {}     
def memo_knapsack(weights=[], values=[], current_capacity=0, current_item=0):
    # base case
    if current_capacity == 0 or current_item == 0:
        return 0
  
    # if current states in memo,
    # return the value
    if (current_item, current_capacity) in MEMO:
        return MEMO[(current_item, current_capacity)]
  
    # recursion
  
    # in case the current item is heavier
    # than the space left in the bag (=bag capacity)
    if weights[current_item] > current_capacity:
        # exclude
        res = memo_knapsack(weights, values, current_capacity, current_item-1)
  
    # in case the current item is equal or less
    # you have 2 choices exclude or include
    # whatever makes the maximum profit
    if weights[current_item] <= current_capacity:
        # exclude
        item_exclusion = memo_knapsack(weights, values, current_capacity, current_item-1)
      
        # include
        current_value = values[current_item]
        updated_capacity = current_capacity-weights[current_item]
        item_inclusion = current_value + memo_knapsack(weights, values, updated_capacity, current_item-1)
        res = max(item_exclusion,
                  item_inclusion)
  
    # store in memo
    MEMO[(current_item, current_capacity)] = res 
      
    return res

נבדוק:

weights = [4, 1, 2, 3]
values =  [4, 8, 1, 8]
max_weight = 6
res = memo_knapsack(weights, values, max_weight, len(values)-1)
print(res) # 17

יעילות הקוד מבחינת הזמן time complexity היא לכל היותר:

O(N*W)

כאשר N הוא מספר הפריטים ו-W הוא הקיבולת המקסימלית של השק. אם הדברים לא מספיק ברורים בסעיף הבא נכנס לזה יותר לעומק.

יעילות הקוד מבחינת זמן הביצוע מראה שיפור משמעותי יחסית לערך האקספוננציאלי כשעובדים עם רקורסיה, ועדיין יש שתי בעיות עם שימוש ב-memoization: ראשית, נדרש מקום נוסף בזיכרון. שנית, קיימת סכנה של stack overflow בגלל הרקורסיה. כדי למנוע את סכנת ה-stack overflow מוטב להשתמש בלולאות.

פתרון בעיית הקיטבג באמצעות טבלה tabulation

בסעיפים הקודמים ראינו שפתרון רקורסיבי לבעיית הקיטבג אינו יעיל מבחינת time complexity וגם שפתרון רקורסיבי הכולל memoization הוא יעיל משמעותית אבל עדיין עלול לסבול מבעיית הצפת זיכרון, stack overflow הנובעת משימוש ברקורסיה. בחלק הזה נראה פתרון שגם הוא לקוח מהפרדיגמה של תכנות דינמי dynamic programming המשתמש במקום ברקורסיה באיטרציה (לולאה) מה שמאפשר לו להיות יעיל בהרבה. הסיבה בגללה רקורסיה היא יקרה יותר היא בגלל שיש צורך לשמור את כל הקריאות לפונקציה ב-stack memory כדי לאפשר את החזרה לפונקציות הקוראות לפי הסדר. קיבולת ה-stack memory מוגבלת מה שחושף אותנו לסכנה של הצפת זכרון במקרה של עודף קריאות.

במקרה שלנו, נריץ 2 לולאות, אחת בתוך השנייה שייצרו טבלה. כל תא בטבלה יכיל את הפתרון לבעיה קטנה ויקדם אותנו לעבר מציאת הפתרון לבעיה כולה. את הפתרון לבעיה הגדולה נמצא בתא האחרון של הטבלה.

חלק חיוני במציאת פתרון טבלאי tabulation הוא לדעת מהם המצבים states שאחר התפתחותם אנו עוקבים. במקרה שלנו ישנם 2 מצבים: מספר הפריטים וקיבולת השק (בק"ג). מכיוון שיש לנו שני מצבים הטבלה שלנו תכיל שני ממדים:

• השורות ייצגו את הפריטים
• העמודות ייצגו את הקיבולות האפשרויות של השק (בק"ג)

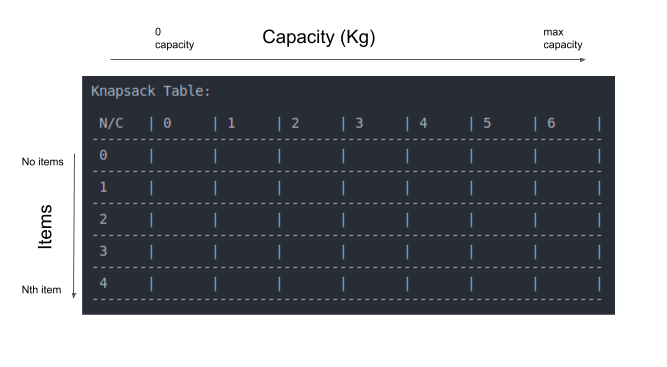
• השורות מתחילות מ-0 כדי לייצג מצב שבו אין פריטים בשק, וכל שורה מוסיפה פריט 1 עד לשורה האחרונה המייצגת את המספר המקסימלי של הפריטים.
• העמודות מתחילות מ-0 כדי לייצג מצב בו קיבולת השק היא 0, וכל עמודה מוסיפה ק"ג 1 לקיבולת עד שמגיעים לקיבולת המרבית.
• אפשר להחליט לשים את הפריטים בעמודות ואת המשקלים בשורות. זה לא משנה. אבל אחרי שבוחרים צריך להתמיד בבחירה עד שמסיימים לפתור.

כל תא בטבלה מייצג פתרון של בעיה קטנה. במקרה שלנו זה הערך של התא ב-$ עבור שילוב המצבים: מספר פריט וקיבולת השק.

הפתרונות קשורים. אנחנו פותרים תא אחד, ועוברים לפתור את התא הבא. כאשר הפתרון של התא הבא מבוסס על הפתרון של התא הקודם.

נעבור על כל אחד מהתאים, ונראה איך לפתור את הבעיות.

בשורה הראשונה יש לנו 0 פריטים ולכן הערכים בכל התאים של השורה יהיו 0:

מה שמעניין אותנו בכל שורה הוא האם אנחנו צריכים להכניס את הפריט הנוכחי לשק או להשאיר אותו בחוץ. במידה והפריט הנוכחי נשאר בחוץ מעתיקים את הערך הרשום באותה עמודה בשורה מעל (כי השורה מעל מייצגת את המצב בו הפריט הנוכחי נשאר מחוץ לשק).

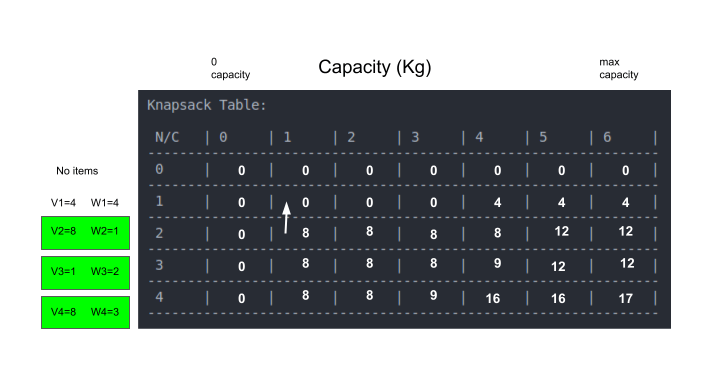
נסתכל על התא הראשון בשורה המייצגת את פריט 1 שמשקלו 4 ק"ג (w1=4) והערך שלו 4$ (v1=4):

• משקל הפריט 4 (w1=4). קיבולת השק היא 0 ק"ג. בתנאים אילה השק לא יכול להכיל את הפריט לכן נעתיק את הערך 0 הרשום בתא מעל בשורה הקודמת.

גם תאים המאפשרים קיבולת של 1, 2 ו-3 ק"ג אינם מאפשרים את מילוי השק. לפיכך, נעתיק לתוכם את הערכים מהשורה שמעל:

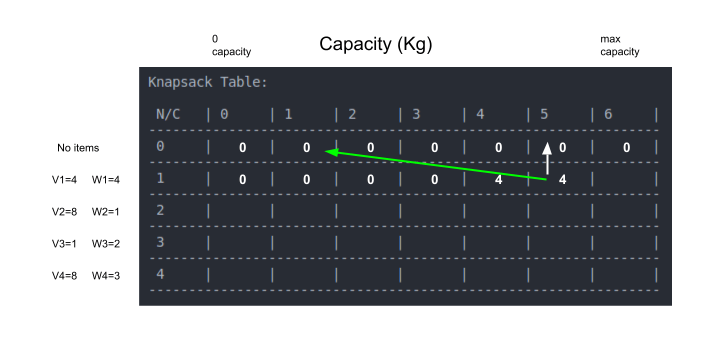
בתא המאפשר קיבולת של 4 ק"ג ניתן להכיל את הפריט. במקרה זה אנחנו צריכים לבחור בין שתי אפשרויות להכניס את הפריט לשק או להשאיר בחוץ. את שתי האפשרויות סימנתי בתמונה באמצעות חיצים:

• האפשרות הראשונה היא להשאיר את הפריט מחוץ לשק. אילו היינו עושים זאת היינו צריכים להעתיק את הערך 0 מהתא מעל. אפשרות זו מסומנת בחץ לבן.

• האפשרות השנייה היא להכניס את הפריט לשק. לשם כך, מוסיפים את הערך של הפריט (v1=4) לערך המתקבל כשקיבולת השק פוחתת בהתאם למשקל הפריט. ראה חץ ירוק בתמונה לעיל.

• במקרה זה בחרנו, מבין שתי האפשרויות, להוסיף את הפריט לשק בגלל שהרווח (4$) עולה על הרווח במקרה שמשאירים את הפריט מחוץ לשק (0$).

אנחנו עדיין בשורה השנייה. התאים שקיבולם 5 ו-6 ק"ג יכולים גם הם להכיל את הפריט שמשקלו 4 ק"ג פעם 1. גם בגלל הקיבולת וגם בגלל שאפשר לבחור פריט לכל היותר פעם אחת:

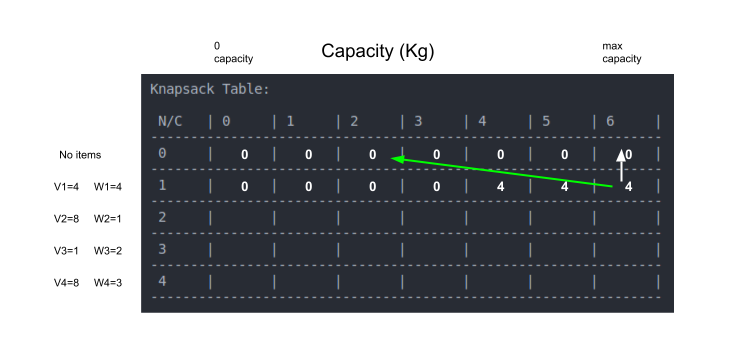
נעבור לשורה השלישית המייצגת את פריט מספר 2 שמשקלו 1 ק"ג.

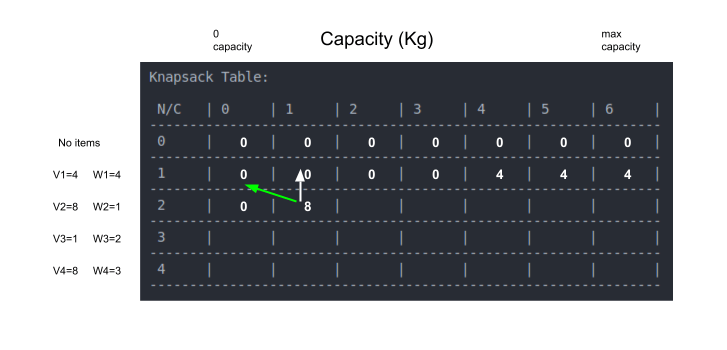
כאשר הקיבולת היא 0 לא ניתן לשבץ פריטים.

כאשר הקיבולת היא 1 ק"ג ניתן לשבץ את הפריט (החץ הירוק בתמונה לעיל).

הקיבולת של 2 - 4 ק"ג גם היא מספיקה כדי להכיל את הפריט השני בלבד. כאשר הקיבולת היא 5 ק"ג התא יכול להכיל את שני הפריטים, הפריט הראשון והשני שמשקלם המשותף 5 ק"ג.

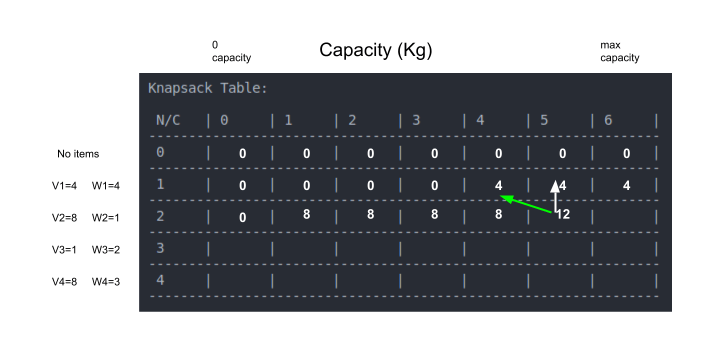
• הבחירה היא בין לוותר על הפריט השני ואז להעתיק את הערך של הפריט הקודם (חץ לבן) לבין לקחת את הפריט השני מה שאומר שנוסיף $8 לערך הפריט הקודם עבור קיבולת הנמוכה ב-1 ק"ג (משקל הפריט הנוכחי) מהקיבולת הנוכחית (5 ק"ג). הכללת הפריט נותנת ערך $ גבוה יותר לכן נבחר בה (החץ הירוק).

בדרך זו נעבור ונמשיך למלא את כל התאים - משמאל לימין ומלמעלה למטה, כל תא נמלא על פי התוצאות בתאים הקודמים, עד שנגיע לתא האחרון שבו נמצא את הפתרון לבעיה שלנו.

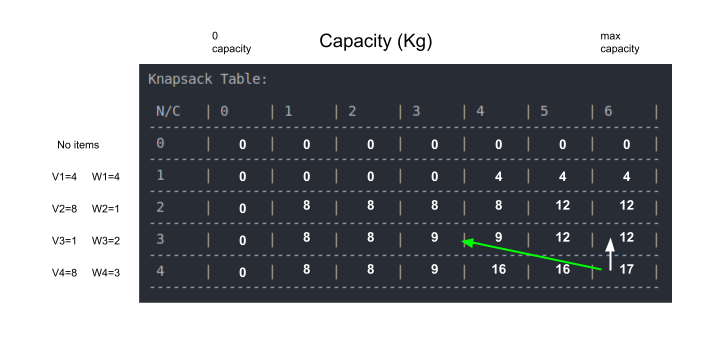
נכתוב את הקוד לפתרון בעיית הקיטבג באמצעות תכנות דינמי ושיטת הטבלה.

נבנה טבלה שמספר העמודות שלה נקבע על פי הקיבולת המקסימלית + 1 (כי מתחילים מקיבולת 0) ומספר השורות שלה נקבע על פי כמות הפריטים + 1 (כי מתחילים מ-0 פריטים).

def tbl_knapsack(max_weight=0, weights=[], values=[]):
   num_items = len(values)
  
   possible_items = range(0, num_items+1)
   possible_weights = range(0, max_weight+1)
  
   # [[each cell] each row]
   # [[each weight] each item]
   table = [[-1 for _ in possible_weights] for _ in possible_items]

• את הטבלה בנינו באמצעות list comprehensions של פייתון כשכל תאי הטבלה מקבלים את הערך הראשוני -1.

את הטבלה אנחנו ממלאים באמצעות 2 לולאות שרצות אחת בתוך השנייה. חיצונית שרצה מלמעלה למטה (מ-0 פריטים ועד לפריט האחרון) ופנימית שרצה משמאל לימין (מקיבולת 0 לקיבולת המרבית).

# fill the table with the values
# for each cell find the combination of items
# that gives the highest value
for current_item in possible_items:
    for current_capacity in possible_weights:
        pass

במידה ומספר הפריטים או הקיבולת הם 0, נציב לתוך התא של הטבלה את הערך 0:

for current_item in possible_items:
    for current_capacity in possible_weights:
        # should we include the current item?
        if current_item == 0 or current_capacity == 0:
            table[current_item][current_capacity] = 0

במידה והקיבולת קטנה ממשקל הפריט אין ברירה חייבים להשאיר את הפריט מחוץ לשק. בהתאם, הערך אותו נרשום בטבלה ישאר כפי שהיה אצל הפריט הקודם עבור אותה קיבולת (אותה עמודה בשורה הקודמת):

for current_item in possible_items:
    for current_capacity in possible_weights:
        # should we include the current item?
        if current_item == 0 or current_capacity == 0:
            table[current_item][current_capacity] = 0
        elif current_capacity < weights[current_item-1]:
            # since we exclude the current item
            # the values don't change
            # from the previous item
            table[current_item][current_capacity] = table[current_item-1][current_capacity]

במידה וקיבולת השק מספיקה כדי להכיל את הפריט הנוכחי צריך לבחור את האפשרות הנותנת את הערך המרבי בין שתי אפשרויות:

• כשהפריט נשאר מחוץ לשק
• כשהפריט נכלל בתוך השק

for current_item in possible_items:
       for current_capacity in possible_weights:
           # should we include the current item?
           if current_item == 0 or current_capacity == 0:
               table[current_item][current_capacity] = 0
           elif current_capacity < weights[current_item-1]:
               # since we exclude the current item
               # the values don't change
               # from the previous item
               table[current_item][current_capacity] = table[current_item-1][current_capacity]
           else: # current_capacity >= current weight
              
               # goal : find the highest value
               # by choosing between exclusion and inclusion of the item
              
               # in the case of inclusion -> add the values of the current item
               # to the values of the previous item in the case that the weight
               # is the current_capacity minus the current item weight
               table[current_item][current_capacity] = max(table[current_item-1][current_capacity],
                                                           values[current_item-1] +
                                                           table[current_item-1][current_capacity-weights[current_item-1]])

הקוד המלא לפתרון בעיית הקיטבג באמצעות טבלה של תכנות דינמי:

def tbl_knapsack(max_weight=0, weights=[], values=[]):
    num_items = len(values)
  
    possible_items = range(0, num_items+1)
    possible_weights = range(0, max_weight+1)
  
    # [[each cell] each row]
    # [[each weight] each item]
    table = [[-1 for _ in possible_weights] for _ in possible_items]
  
    # fill the table with the values
    # for each cell find the combination of items
    # that gives the highest revenue
    for current_item in possible_items:
        for current_capacity in possible_weights:
            # should we include the current item?
            if current_item == 0 or current_capacity == 0:
                table[current_item][current_capacity] = 0
            elif current_capacity < weights[current_item-1]:
                # since we exclude the current item
                # the values don't change
                # from the previous item
                table[current_item][current_capacity] = table[current_item-1][current_capacity]
            else: # current_capacity >= current weight
              
                # goal : find the highest value
                # by choosing between exclusion and inclusion of the item
              
                # in the case of inclusion -> add the values of the current item
                # to the values of the previous item in the case that the weight
                # is the current_capacity minus the current item weight
                table[current_item][current_capacity] = max(table[current_item-1][current_capacity],
                                                           values[current_item-1] +
                                                           table[current_item-1][current_capacity-weights[current_item-1]])
    
    # printKnapsack(table)
    # return whichItems(table, weights)


    return table[num_items][max_weight]

יעילות הקוד מבחינת זמן time complexity היא:

O(N*W)

בהתאם למימדי הטבלה כאשר N הוא מספר הפריטים ו-W הוא המשקל המקסימלי.

הדפסת טבלה יכולה לסייע בהבנת הצעדים אותם נקטה התוכנה בדרך לפתרון הבעיה. נשתמש בפונקציה printKnapsack להדפסת טבלת הפתרונות:

שאלה נוספת מעניינת היא אילו פריטים נכללו בשק. האינטואיציה מאחורי התשובה לשאלה היא שפריט נכלל בשק במידה והערך שלו בשורה שמייצגת אותו גבוה יותר מהערך בשורה המייצגת את הפריט הקודם.

נתחיל מהתא האחרון של הטבלה אותו נשווה לערך בתא המקביל בשורה מעל:

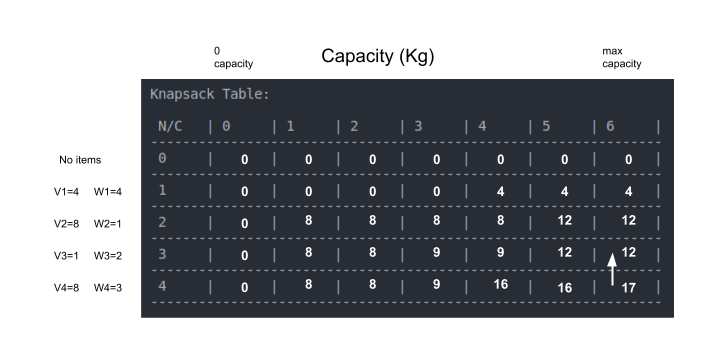
הערך בתא מעל נמוך יותר לכן הפריט הרביעי נמצא בשק.

אחרי שאנחנו יודעים שהפריט הרביעי נמצא בשק, נפחית את קיבולת השק כמשקל הפריט הרביעי. מה שיותיר לנו קיבולת של 3 ק"ג עבור הפריט השלישי.

כדי לדעת האם הפריט השלישי נמצא בשק נשווה לתא שמעליו. אפשר לראות שהתא מעל מכיל ערך נמוך יותר לכן גם הפריט השלישי נמצא בשק:

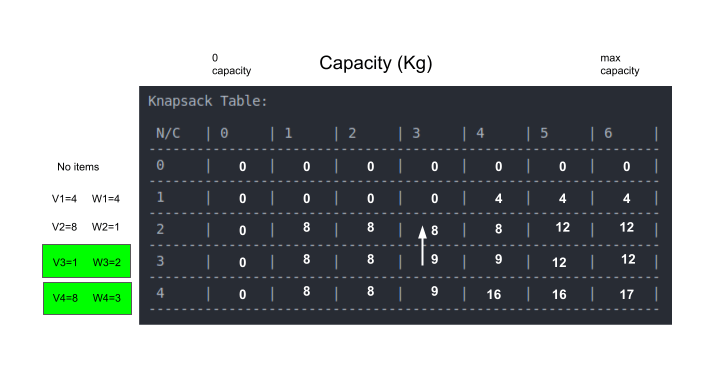
המשקל של הפריט השלישי הוא 2 אז נפחית את קיבולת השק גם כן ב-2 מה שמשאיר לנו קיבולת 1 ק"ג עבור הפריט השני:

מההשוואה עם השורה מעל אנחנו יכולים לראות הפרש המלמד על הכללת הפריט השני גם כן בשק:

כיוון שהגענו לקיבולת 0 כבר לא נוכל להכליל פריטים נוספים בשק.

הפונקציה למציאת הפריטים שנכנסו לשק מקבלת את הטבלה table אותה יצרה הפונקציה tbl_knapsack ואת משקלי הפריטים בתור פרמטרים ומחזירה את מערך הפריטים שנכנסו לשק. הפונקציה רצה בלולאה יורדת מהפריט האחרון של הטבלה כשבכל איטרציה היא עוברת לטפל בפריט הקודם (בשורה הקודמת) ואם הפריט בשורה הנוכחית בעל ערך גבוה יותר היא גם מורידה את המשקל שלו מקיבולת השק.

def whichItems(table, weights):
    items = []
  
    last_row = len(table) - 1
    last_col = len(table[0]) - 1


    col = last_col
    # starting from the last table cell
    # compare the cell value to the row above -
    # a difference is due to inclusion of the item
    # that the row represents in the knapsack
    # each iteration decreases the row index by 1
    # starting from the last row
    # in case of inclusion shift the column index number
    # by the weight of the current item
    for row in range(last_row, -1, -1):
        if table[row][col] > table[row-1][col]:
            items.append(row)
            col = col - weights[row-1]
    items.sort()
         
    return items

• הפונקציה sort מסדרת את הפריטים לפי סדר עולה כיוון שהפונקציה מוצאת את הפריטים בסדר יורד.

ננסה את הפתרון שכתבנו:

weights = [4, 1, 2, 3]
values =  [4, 8, 1, 8]
max_weight = 6
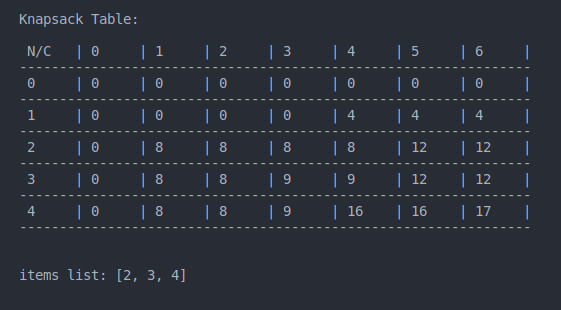
res = tbl_knapsack(max_weight, weights, values)
print(f"items list: {res} ")

התוצאה:

מדריכים נוספים בסדרה ללימוד פייתון

תכנות דינאמי מלמטה למעלה ובחזרה - מדריך לתכנות דינאמי שמתחיל מהבסיס

big-O ביטוי ליעילות הקוד

אלגוריתם חיפוש בינארי - מהבנה ליישום

האלגוריתם Quicksort ותהליך החלוקה

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים