חידה תכנותית : מציאת האב המשותף הנמוך ביותר LCA בעץ בינארי
האב המשותף הנמוך ביותר (LCA = Lowest Common Ancestor) של שני צמתים השייכים לעץ בינארי, p ו-q, הוא הצומת הרחוק ביותר משורש העץ שיש לו את שני הצמתים כצאצאים.
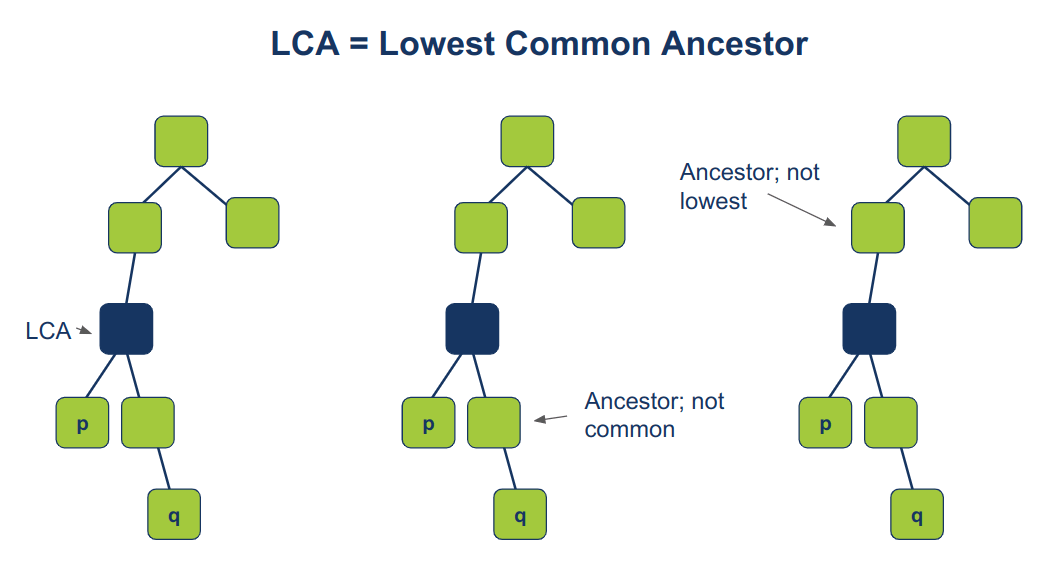
עליך לכתוב פונקציה שמוצאת את ה-LCA של עץ נתון עבור שני הצמתים: p ו-q.
הנחות:
- כל צמתי העץ הם ייחודיים. אין צומת שמופיע יותר מפעם אחת בעץ.
- שני צמתי המטרה, p ו-q , נמצאים בעץ.
- אחד מצמתי המטרה עשוי להיות ה-LCA. לדוגמה, אם q הוא ההורה של p אז q הוא ה-LCA.
הסבר הפתרון
האלגוריתם מבוסס על מעבר על עץ בינארי בגישה של DFS רקורסיבי במטרה לאתר את האב המשותף הנמוך ביותר LCA עבור שני צמתי מטרה p ו-q.
נבחין בין שני מצבים:
-
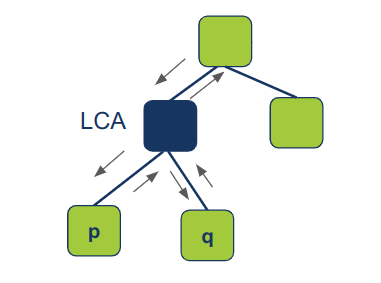
במידה ושני הצאצאים, הימני והשמאלי, מחזירים תוצאה אז הצומת הנוכחי הוא בהכרח ה-LCA. בגלל שהאלגוריתם משתמש בסריקה רקורסיבית אשר ממשיכה לסרוק עד שהיא מגיעה לצומת עלה (ללא צאצאים) ואז הסריקה מתחילה להחזיר תוצאות מלמטה.
-
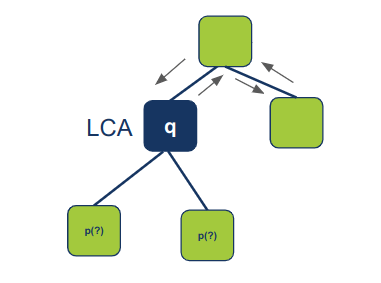
אם רק אחד מהצאצאים, הימני או השמאלי, מחזיר תוצאה אז הוא הוא בהכרח ה- LCA, כי ההנחה היא ששני הצמתים נמצאים בעץ ואם אינם נמצאים בתת עץ אחד הם חייבים להימצא בשני.
-
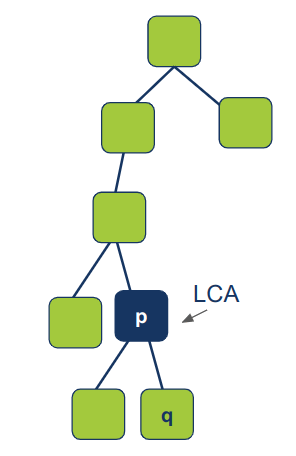
שים לב שהאלגוריתם לא עובד עבור המקרה שבו רק אחד הצמתים נמצא בעץ והשני לא בגלל שהוא ההנחה בשאלה ששני צמתי המטרה בהכרח קיימים בעץ.
-
הפונקציה LCA היא רקורסיבית. היא מקבלת שלושה פרמטרים: current_node שהוא הצומת ממנו יש להתחיל את הסריקה בכל שלב, ושני ערכים, p ו-q, שהם הערכים של צמתי המטרה.
def lca(current_node, p, q): -
טיפול במקרה בסיס: במידה והפונקציה מקבלת current_node שהוא None אז היא מחזירה None כי הגענו לקצה הסריקה, ואין אפשרות להתקדם יותר.
if not current_node: return None במידה והצומת הנוכחי current_node הוא בעל ערך זהה למטרות, p או q, אז הפונקציה מחזירה את הצומת הנוכחי כי היא מצאה את אחת המטרות שהיא מחפשת.
if current_node.data in {p, q}: return current_node-
במידה והפונקציה לא מצאה את אחת המטרות אז היא ממשיכה לחפש באופן רקורסיבי, על ידי קריאות חוזרות לפונקציה, עבור תת העץ השמאלי והימני.
left_lca = lca(current_node.left, p, q) right_lca = lca(current_node.right, p, q) -
במידה ורק תת עץ אחד מתתי העצים, הימני או השמאלי, מחזיר תוצאה אז שני צמתי המטרה נמצאים בתת עץ זה, לפיכך נחזיר את המטרה שנמצאה.
if not left_lca: return right_lca if not right_lca: return left_lca -
אם שני תתי העצים מחזירים תוצאה, הצומת הנוכחי הוא בהכרח ה-LCA.
return current_node
הקוד לפתרון אתגר ה-LCA
הקוד הבא מיישם את האלגוריתם:
הקלאס Node הוא קוד סטנדרטי ליישום עצים בינאריים:
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = Noneהפונקציה למציאת האב המשותף הנמוך ביותר-LCA:
def lca(current_node, p, q):
# Base case: If the current node is empty (None),
# return None (no common ancestor).
if not current_node:
return None
# If the current node is one of the target nodes, it is the LCA.
if current_node.data in {p, q}:
return current_node
# Search recursively in the left and right subtrees.
left_lca = lca(current_node.left, p, q)
right_lca = lca(current_node.right, p, q)
# Assuming both targets exist in the tree:
# If no target node is found in one of the two subtrees,
# both targets must exist in the other subtree.
if not left_lca:
return right_lca
if not right_lca:
return left_lca
# If both target nodes are found, the root must be the LCA.
return current_node
נבחן את הקוד:
# Test cases
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.left.left = Node(5)
root.left.left.right = Node(6)
root.left.left.right.right = Node(7)
# Target nodes are the same
res = lca(root, 4, 4)
if res:
print(res.data)
else:
print("No LCA found")
# Nodes on both sides
res = lca(root, 5, 7)
if res:
print(res.data)
else:
print("No LCA found")
# One of the nodes is a parent of the other
res = lca(root, 6, 7)
if res:
print(res.data)
else:
print("No LCA found")
# Nodes on both sides
res = lca(root, 3, 7)
if res:
print(res.data)
else:
print("No LCA found")
# Target nodes are the same
res = lca(root, 4, 4)
if res:
print(res.data)
else:
print("No LCA found")
# Target nodes not in the tree
res = lca(root, 40, 70)
if res:
print(res.data)
else:
print("No LCA found")
# Only one of the nodes in the tree
res = lca(root, 40, 7)
if res:
print(res.data)
else:
print("No LCA found")
נסביר:
הסריקה הרקורסיבית מתקדמת מצומת השורש של העץ במורד העץ עד הגעה לצמתים העלים או לצמתי המטרה ומשם התוצאה מוחזרת כל הדרך חזרה לצומת השורש, וכשמגיעים אליו הפונקציה מחזירה תוצאה.
הערכת ביצועים
הפונקציה מבקרת ב- N הצמתים של העץ לכל היותר פעם אחת בכל צומת, ולפיכך סיבוכיות הזמן היא לינארית O(N)
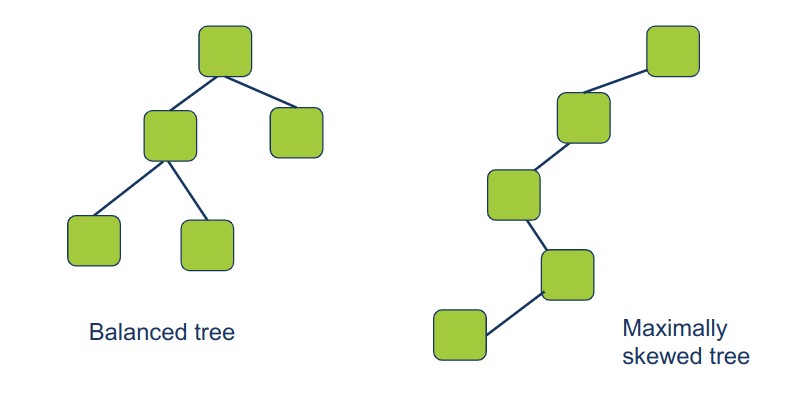
סיבוכיות המקום נקבעת על ידי העומק המרבי של מחסנית קריאות הפונקציה stack במהלך הקריאות הרקורסיבית. במקרה של עץ מאוזן, העומק המרבי הוא לוגריתמי O(LOG N), מה שמוביל לסיבוכיות לוגריתמית. במקרה הגרוע ביותר (עץ מוטה), הסיבוכיות עלולה במקרה הגרוע להיות לינארית O(N).
מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך
יישום עץ בינארי בפייתון - המדריך למתחילים
אלגוריתם חיפוש לעומק DFS - מהבנה ליישום
חידה תכנותית : סריקת עץ בינארי על פי סדר הרמות
לכל המדריכים בסדרה ללימוד פייתון
אהבתם? לא אהבתם? דרגו!
0 הצבעות, ממוצע 0 מתוך 5 כוכבים


המדריכים באתר עוסקים בנושאי תכנות ופיתוח אישי. הקוד שמוצג משמש להדגמה ולצרכי לימוד. התוכן והקוד המוצגים באתר נבדקו בקפידה ונמצאו תקינים. אבל ייתכן ששימוש במערכות שונות, דוגמת דפדפן או מערכת הפעלה שונה ולאור השינויים הטכנולוגיים התכופים בעולם שבו אנו חיים יגרום לתוצאות שונות מהמצופה. בכל מקרה, אין בעל האתר נושא באחריות לכל שיבוש או שימוש לא אחראי בתכנים הלימודיים באתר.
למרות האמור לעיל, ומתוך רצון טוב, אם נתקלת בקשיים ביישום הקוד באתר מפאת מה שנראה לך כשגיאה או כחוסר עקביות נא להשאיר תגובה עם פירוט הבעיה באזור התגובות בתחתית המדריכים. זה יכול לעזור למשתמשים אחרים שנתקלו באותה בעיה ואם אני רואה שהבעיה עקרונית אני עשוי לערוך התאמה במדריך או להסיר אותו כדי להימנע מהטעיית הציבור.
שימו לב! הסקריפטים במדריכים מיועדים למטרות לימוד בלבד. כשאתם עובדים על הפרויקטים שלכם אתם צריכים להשתמש בספריות וסביבות פיתוח מוכחות, מהירות ובטוחות.
המשתמש באתר צריך להיות מודע לכך שאם וכאשר הוא מפתח קוד בשביל פרויקט הוא חייב לשים לב ולהשתמש בסביבת הפיתוח המתאימה ביותר, הבטוחה ביותר, היעילה ביותר וכמובן שהוא צריך לבדוק את הקוד בהיבטים של יעילות ואבטחה. מי אמר שלהיות מפתח זו עבודה קלה ?
השימוש שלך באתר מהווה ראייה להסכמתך עם הכללים והתקנות שנוסחו בהסכם תנאי השימוש.