חידה תכנותית : סריקת עץ בינארי על פי סדר הרמות

בהינתן השורש `root` של עץ בינארי, עליך לכתוב פונקציה שמחזירה את סדר הצמתים כאשר עוברים על העץ משמאל לימין רמה אחר רמה.

לדוגמה:

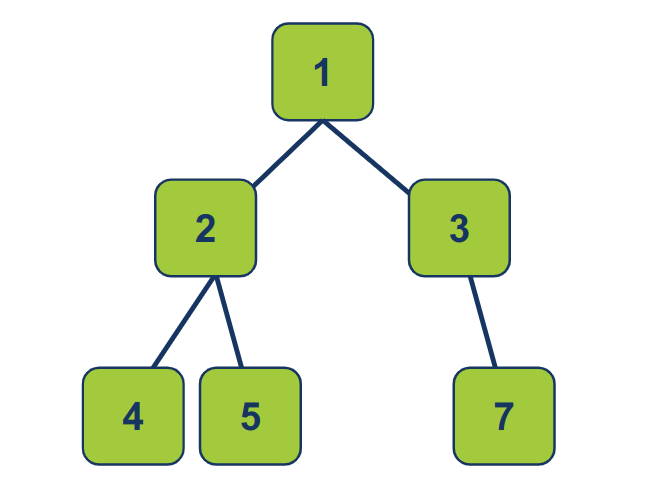
Input: root = [1, 2, 3, 4, 5, None, 7]
Output: [[1], [2, 3], [4, 5, 7]]

דוגמאות נוספות:

Input: root = [1]
Output: [[1]]

Input: root = []
Output: []

הרעיון שמאפשר לפתור את הבעיה ביעילות

בשביל לפתור את הבעיה צריך לבקר בצמתים ברמה נמוכה יותר לפני שעוברים לבקר בצמתים ברמה גבוהה יותר, מה שעושה ביעילות רבה אלגוריתם חיפוש לרוחב BFS שנעזר במבנה נתונים תור Queue לצורך קביעת סדר הביקור בצמתי העץ. כאשר מבקרים בצומת מסוים מסירים את הצומת הזה מהתור ומוסיפים את הילדים של הצומת לתור. דבר המבטיח ביקור בצמתים ההורים לפני שמבקרים בצמתים הילדים עבור כל רמה בנפרד. השימוש באלגוריתם BFS ובמבנה נתונים תור queue מאפשר סקירה שיטתית של העץ הבינארי, ומספק סדר לביקור בצמתים לפי סדר הרמות.

הפתרון וההסבר

להלן הפתרון המלא, ההסבר בהמשך:

class TreeNode:
   def __init__(self, data):
       self.data = data
       self.left = None
       self.right = None


def level_order_traversal(root):
   levels = []
   # Handle the case in which the tree is None
   if not root:
      return levels
  
   # Initialize a queue for implementing BFS
   q = [root]
  
   while q:
       # Each level takes a separate array in the results
       level = []
      
       # Capture the number of nodes in the current level
       q_len = len(q)
      
       # Traverse the current level
       for _ in range(q_len):
          
           # Dequeue the front node
           current = q.pop(0)


           # Use only if isn't None
           if current:
               level += [current.data]
              
               # Enqueue the left and right children for the next iteration
               q += [current.left]
               q += [current.right]
       # If the level is not empty, add it to the result
       if level:
           levels += [level]
  
   return levels

נבחן את הפונקציה `level_order_traversal`:

# Binary tree to traverse
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
#root.right.left = Node(6)
root.right.right = Node(7)
root.right.right.left = Node(8)


print(level_order_traversal(root)) # [[1], [2, 3], [4, 5, 7], [8]]


root = Node(1)
print(level_order_traversal(root)) # [[1]]


root = None
print(level_order_traversal(root)) # []

נסביר.

1. הגדרת הפונקציה:

   def level_order_traversal(root):

   • הפונקציה level_order_traversal() מקבלת פרמטר `root`. ה-`root` הוא הצומת ממנו מתחילה סריקת העץ.

2. אתחול משתנים:

   levels = []

   • המשתנה `levels` מאותחל כרשימה ריקה אשר תשמש לאחסון הצמתים של העץ הבינארי בכל רמה.

   נאתחל בנוסף משתנה תור Queue:

   q = [root]

   • הרשימה `q` מאותחלת עם צומת ה-`root`. רשימה זו משמשת בתור Queue כדי ליישם את אלגוריתם חיפוש לרוחב (BFS). תור הוא מבנה נתונים שפועל לפי סדר FIFO (First-In, First-Out). במקרה זה, התור ישמש ליישום חיפוש לרוחב (BFS), שהוא שיטה למעבר על עץ רמה אחר רמה. צומת השורש מתווסף לתור כדי לאתחל את המעבר.

3. עיקר העבודה של האלגוריתם BFS מתבצע בתוך לולאה שתמשיך לרוץ כל עוד התור Queue אינו ריק מה שאומר שהלולאה תמשיך לרוץ כל עוד קיימים צמתים שטרם ביקרנו בהם:

   while q:

   בתוך הלולאה החיצונית:

   1. הדבר הראשון שעושים בתוך הלולאה הוא לאתחל מערך ריק לאחסון הצמתים של הרמה הנוכחית:

      level = []

   2. נאתחל משתנה שיאחסן את מספר הפריטים העכשוויים בתור במספר זה נשתמש להגבלת מספר הפעמים שהלולאה הפנימית תרוץ:

      q_len = len(q)

   3. מעבר על הרמה הנוכחית בתוך לולאה פנימית:

      for _ in range(q_len):

      • שורה זו מתחילה לולאה פנימית שתעבור על כל הצמתים ברמה הנוכחית של העץ. המשתנה `_` הוא מחזיק מקום במקום משתנה.

      בתוך הלולאה הפנימית:

      • מסירים את הצומת הקדמי מהתור ומציבים במשתנה `current`:

        current = q.pop(0)

      • במידה והצומת הנוכחי אינו `None` נוסיף אותו למערך הרמה הנוכחית:

        if current: level += [current.data]

      • נוסיף את צאצאי הצומת הנוכחי הימני והשמאלי לתור בשביל שהלולאה תמשיך לרוץ:

        q += [current.left]
        q += [current.right]

   4. ביציאה מהלולאה הפנימית, במידה ומערך הרמה הנוכחית אינו ריק, נוסיף אותו למערך התוצאות הסופי:

      if level: levels += [level]

4. לבסוף, הפונקציה מחזירה את מערך התוצאות הסופי:

   return levels

הערכת ביצועים

מורכבות זמן: O(N) כאשר `N` הוא מספר הצמתים בעץ הבינארי מכיוון שהשימוש בתור Queue ואלגוריתם BFS מבטיח ביקור בכל אחד מצמתי העץ בדיוק פעם אחת.

מורכבות מקום: O(N) כאשר N הוא מספר הצמתים בעץ הבינארי כאשר מורכבות המקום נובעת משני משתנים `q` המהווה את התור ו-levels שהוא התוצאה המוחזרת. האורך של שניהם מוגבל ל-`N` פריטים לכל היותר.

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

חידה תכנותית : מציאת האב המשותף הרחוק ביותר LCA בעץ בינארי

אלגוריתם חיפוש לרוחב BFS

תורים Queues - הבנה ויישום בפייתון

יישום עץ בינארי בפייתון - המדריך למתחילים

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים