אלגוריתם חיפוש לעומק DFS - מהבנה ליישום

סריקה traversal היא תהליך של ביקור וחקירה של כל הצמתים השייכים לגרף באופן שיטתי. סריקה היא פעולה יסודית המשמשת באלגוריתמים שונים כדי לנתח או לשנות את מבנה הגרף והנתונים המופיעים בו.

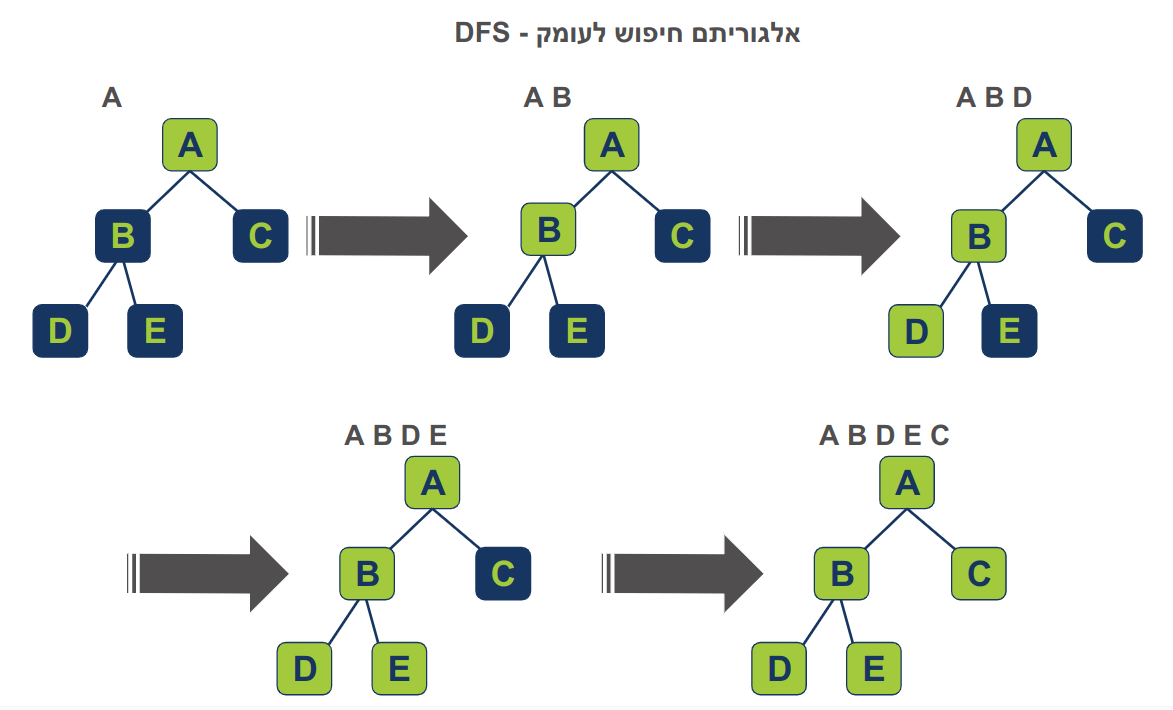
אלגוריתם חיפוש לעומק Depth First Search (DFS) הוא אחד מאלגוריתמי הסריקה המקובלים ביותר המשמשים לסרוק explore ולבקר visit בכל הצמתים של גרף פעם אחת בכל צומת באופן שיטתי. הוא מתחיל מצומת מוצא וסורק רחוק ככל האפשר לאורך ענף עד סופו לפני שהוא חוזר על עקבותיו backtrack. מכאן השם "חיפוש לעומק".

ניתן להשתמש ב-DFS לסריקה של גרפים מכוונים או לא מכוונים, ובכלל כך עצי נתונים. הוא יכול להתמודד עם גרפים לא מחזוריים או כאלה המכילים הפניות מחזוריות, אך חשוב לעקוב אחר הצמתים בהם ביקר כדי להימנע מלהיתקע בחזרות אינסופיות.

כדי לעקוב אחר הצמתים הנסרקים סריקת DFS משתמשת בערימה stack (אפשר גם ברקורסיה המחקה את מבנה הנתונים באמצעות call stack).

ביצוע אלגוריתם DFS כולל 4 שלבים:

1. מתחילים מצומת מוצא אותו מניחים בראש הערימה stack.
2. לוקחים את הצומת הנוכחי מראש הערימה. מסמנים כ-visited כדי להימנע מביקור נוסף בו.
3. עוברים על כל שכני הצומת הנוכחי בהם טרם ביקרנו ומוסיפים לראש ה-stack.
4. חוזרים על 2 ו-3 עד לריקון ה-stack בגלל שעברנו על כל הצמתים של הגרף.

ניתן להשתמש באלגוריתם DFS למגוון משימות. לדוגמה:

1. חיפוש נתיב וחיבוריות:DFS יכול לשמש כדי למצוא את כל הנתיבים המחברים בין שני צמתים או כדי לקבוע האם צמתים שייכים לאותו הגרף.
2. ביצוע מיון טופולוגי כאשר מסדרים משימות תוך התחשבות בתלויות. במילים פשוטות, אם משימה B תלויה ב-A אז האלגוריתם יאתר את התלות וימצא שצריך לבצע את A לפני B.
3. DFS יכול לשמש כדי לגלות הפניות מעגליות בגרף. בהמשך נראה איך זה עובד.
4. מציאת רכיבי חיבור בגרף כפי שנסביר בהמשך המדריך.
5. לצורך סריקה של עצי נתונים (שהם סוג מיוחד של גרף) לפי סדר pre-order, in-order, או post-order.

ראוי לציין ש- DFS לא תמיד מבטיח את הנתיב הקצר ביותר בין שני צמתים. לצורך מציאת הנתיב הקצר נשתמש באלגוריתמים אחרים כמו חיפוש לרוחב Breadth First Search (BFS) או אלגוריתם דייקסטרה Dijkstra.

בסך הכל, חיפוש לעומק DFS הוא אלגוריתם חשוב ונפוץ לחקר וניתוח גרפים ובהתאם יש לו טווח רחב של יישומים.

יישום חיפוש לעומק DFS באמצעות קוד פייתון

עכשיו כשאנחנו מכירים את האלגוריתם לביצוע חיפוש לעומק DFS, נעבור ליישם אותו בפייתון באמצעות הפונקציה הבאה המשתמשת ברקורסיה:

def dfs(current_node, graph, visited=None):
    # If visited is None (i.e., not provided in the function call), create a new set to store visited nodes.
    if visited is None:
        visited = set()

    # Mark the current node as visited
    visited.add(current_node)
    
    # Process current node
    print(current_node, end=", ")  

    # Recursively visit all the unvisited neighbors of the current node
    for neighbor in graph[current_node]:
        # By definition, DFS algorithm visits nodes only once
        if neighbor not in visited:
            # Recursive call
            dfs(neighbor, graph, visited)

נבדוק את הפונקציה ליישום DFS באמצעות הקוד הבא:

# Example usage:
# An example of an adjacency list representation of a graph
graph = {
            'A': ['B', 'C'],
            'B': ['A', 'D', 'E'],
            'C': ['A', 'F', 'G'],
            'D': ['B'],
            'E': ['B'],
            'F': ['C'],
            'G': ['C']
}
start = 'A'
dfs(start, graph)

הסבר על הפונקציה dfs():

1. הפונקציה dfs() מיישמת את אלגוריתם DFS (חיפוש לעומק) כדי לסקור את כל הגרף החל מצומת המקור current_node אותו היא מקבלת כפמרטר.
2. המשתנה graph מיוצג כרשימת סמיכויות adjacency list.
3. הסט visited משמש לעקוב אחר הצמתים בהם הפונקציה ביקרה . הוא מוגדר בתחילה כ-None ברשימה הפרמטרים של הפונקציה כדי למנוע בעיה נפוצה שאם מעבירים לפייתון פרמטר ברירת מחדל שהוא mutable (דוגמת סט, מערך או מילון) אז במקום ליצור אותו בכל פעם שקוראים לפונקציה מחדש הוא משתמש באותו אחד. במידה ומתקיים התנאי הבודק אם הסט visited הוא None הפונקציה יוצרת סט חדש visited בתוך גוף הפונקציה. מה שמונע את הבעיה.
4. הפונקציה מסמנת את current_node כמי שביקרו בו על ידי הוספה לסט visited
5. בשלב זה, ניתן להשתמש בצומת (במקרה זה, הוא מודפס).
6. לאחר מכן, הפונקציה עוברת בתוך לולאה על השכנים של current_node. אם שכן אינו בסט visited, זה אומר שהשכן טרם נסרק. במקרה זה, הפונקציה קוראת באופן רקורסיבי לעצמה עבור השכן המוגדר כ-current_node החדש, מה שמבטיח שתהליך הסריקה ימשיך משכן זה.

האופי הרקורסיבי של הפונקציה מבטיח ש-DFS יסרוק לעומק ככל האפשר לאורך כל ענף לפני שהוא יעשה backtracking ויסרוק ענפים אחרים, שטרם נסרקו.

יישום DFS באמצעות לולאה

ניתן ליישם את אלגוריתם DFS באמצעות לולאה במקום באמצעות רקורסיה. לצורך כך מחליפים את הרקורסיה במבנה נתונים ערימה stack.

הפונקציה iterative_dfs() מיישמת את אלגוריתם DFS באמצעות לולאה:

def iterative_dfs(start_node, graph):
    # Store visited nodes
    visited = set()
    
    # Order the nodes to be processed in a LIFO stack
    stack = []
    
    # Mark the start_node as visited
    visited.add(start_node)
    
    # Add the first node to the stack to initialize the DFS process
    stack.append(start_node)
    
    # The actual DFS process runs inside a loop
    # as long as the stack is not empty
    while stack:
        # Get the top item out of the stack
        current_node = stack.pop()
        # Process the current node - do whatever you see fit
        print(current_node, end=", ")
        # Traverse all its neighbors
        for neighbor in graph[current_node]:
            # By definition, DFS algo visits nodes only once
            if neighbor not in visited:
                # Mark as visited to prevent re-visiting
                visited.add(neighbor)
                # Add neighbor to stack
                stack.append(neighbor)

נסביר את היישום של DFS המבוסס על לולאה:

• הפונקציה משתמשת בסט visited למעקב אחר הצמתים בהם ביקר תהליך ה-DFS במטרה להבטיח שביקרנו בכל צומת בדיוק פעם אחת, מה שהופך את הפונקציה ליעילה הרבה יותר ומונע לולאות אינסופיות במקרה של הפניות מעגליות בגרף.
• מבנה נתונים ערימה stack משמש לאחסון צמתים שהאלגוריתם צריך לבקר בהם בהמשך. הצמתים מתווספים לראש הערימה ואחר כך מוסרים מראש הערימה על פי העיקרון המסדר Last-In-First-Out (LIFO), מה שמחקה את ההתנהגות הרקורסיבית של חיפוש עומק DFS.
• הפונקציה מתחילה את תהליך ה-DFS מצומת המקור. היא מוסיפה את הצומת לסט visited ולערימה stack כדי להתחיל את הסריקה.
• תהליך ה-DFS בפועל מתבצע בתוך לולאת while הממשיכה לרוץ עד לריקון הערימה. בכל פעם שהלולאה רצה, הצומת אשר בראש הערימה מוסר (pop), ומעובד. עיבוד הצומת תלוי במקרה השימוש הספציפי. בקוד לעיל, הצומת פשוט מודפס.
• בהמשך, הלולאה עוברת על השכנים של הצומת הנוכחי וקודם כל בודקת אם כבר ביקרו בהם. אם היא מוצאת שכן שטרם ביקרו בו, היא מסמנת אותו כ-visited ואז מוסיפה לראש הערימה. כך היא מבטיחה שאותם השכנים שטרם נסרקו יטופלו בפעמים הבאות בהם הלולאה תרוץ.
• ה-DFS ממשיך לרוץ עד שהערימה מתרוקנת, כלומר כל הצמתים אליהם ניתן להגיע מצומת המקור נסרקו.

הסיבוכיות של אלגוריתם סריקה לעומק DFS

ראינו שני יישומים שונים של אלגוריתם חיפוש לעומק (DFS) ב-Python:

1. DFS רקורסיבי: היישום הראשון השתמש בגישה רקורסיבית כדי לסרוק את הגרף. הפונקציה dfs() הוגדרה רקורסיבית וחיפשה לעומק ככל האפשר לאורך כל ענף לפני חזרה אחורה back track כדי לחקור ענפים נוספים בהם טרם ביקרה.

2. DFS איטרטיבי: היישום השני השתמש בלולאה לצורך סריקת הגרף. הפונקציה iterative_dfs() השתמשה במבנה נתונים ערימה stack כדי לעקוב אחר הצמתים שיש לעבד. במקום להשתמש ב-call stack (כמו בגרסה הרקורסיבית).

שני היישומים משיגים את אותה התוצאה שהיא סריקת כל הצמתים בגרף בדיוק פעם אחת. הם בעלי סיבוכיות זמן זהה אבל ישנו הבדל עיקרי אחד. היישום הרקורסיבי מסתמך על call stack לצורך ניהול סדר הסריקה, מה שעלול להוביל לשגיאת הצפת הזיכרון stack overflow במקרה של גרפים גדולים הדורשים רקורסיה עמוקה. עם זאת, הוא בדרך כלל יותר תמציתי וקל יותר להבין אותו. היישום האיטרטיבי נמנע מבעיות overflow כיוון שהוא משתמש במבנה נתונים stack במקום, אך הוא דורש ניהול מפורש של הערימה ושימוש בקוד תמציתי פחות.

שתי הגישות תקפות, הרקורסיבית והאיטרטיבית, והבחירה ביניהן עשויה להיות תלויה בבעיה שעל הפרק, בגודל הגרף ובהעדפות אישיות.

סיבוכיות זמן:

שני היישומים של אלגוריתם DFS אותם ראינו במדריך, הרקורסיבי והאיטרטיבי, הם בעלי סיבוכיות זמן זהה O(V + E) כאשר V הוא מספר הצמתים בגרף ו-E מספר הקשתות.

חישוב סיבוכיות הזמן O(V + E) נעשה על ידי חיבור התרומות של סך הביקורים בצמתים ובקשתות:

1. ביקור בכל צומת בדיוק פעם אחת תורם O(V)
2. כל קשת יוצאת או נכנסת לגרף פעמיים (כיוון שקשת היוצאת מצומת אחד נכנסת לצומת שני) ומכאן סיבוכיות זמן 2E שהיא למעשה O(E).

שילוב 2 הנקודות לעיל, נותן סיבוכיות זמן O(V + E).

סיבוכיות מקום:

ה-DFS הרקורסיבי והאיטרטיבי הם בעלי סיבוכיות מקום זהה של O(V). מקום זה משמש לאחסון ה-call stack (עומק רקורסיה בגירסה הרקורסיבית) ומבני נתונים מפורשים. דוגמת, הסט visited או הערימה stack בגרסה האיטרטיבית.

חשוב לציין שסיבוכיות המקום עבור DFS יכולה להיות מושפעת מגורמים נוספים כתלות במקרה השימוש. לדוגמה, אם ה-DFS משמש כדי למצוא מסלולים או לאחסן את סדר הסריקה, ייתכן שיהיה צורך במבני נתונים נוספים כמו מערך המסלול או רשימת הסריקה, וסיבוכיות המקום תגדל בהתאם. עם זאת, סיבוכיות המקום העיקרית הקשורה לסריקה עצמה של DFS נותרת O(V).

רכיבי חיבור connected components

בתורת הגרפים, רכיבי חיבור connected components הוא מושג בסיסי המשמש לתיאור המבנה והחיבוריות של גרף. רכיב חיבור של גרף לא-מכוון הוא תת-גרף שבו כל שני צמתים (קודקודים) מחוברים זה לזה לפחות בנתיב אחד. במילים אחרות, ברכיב חיבור ניתן לחבר בין כל זוג צמתים בתוך אותו רכיב.

המושג של רכיבי חיבור connected components הוא שימושי במיוחד בניתוח גרפים, מכיוון שהוא עוזר לזהות ולחקור את קבוצות הצמתים העצמאיות המחוברות בתוך הגרף. קבוצות אלה יכולות לייצג מבנים שונים או קהילות, והבנתן יכולה לחשוף תכונות ויחסים חשובים בתוך הגרף.

כמה נקודות שיסייעו בהבנה של רכיבי חיבור:

• מספר רכיבי החיבור: גרף יכול להיות בעל רכיב חיבור אחד או מספר רכיבי חיבור. אם לגרף יש רק רכיב חיבור אחד, נכנה אותו גרף מחובר . אם לגרף יש מספר רכיבי חיבור, כל רכיב מייצג תת-גרף עצמאי.
• צמתים מבודדים: בהקשר של רכיבי חיבור, צמתים מבודדים (צמתים ללא קצוות) נחשבים כרכיבי חיבור נפרדים. במילים אחרות, הם מטופלים כרכיבים חד-צומתיים.
• גודל רכיב החיבור: גודל רכיב החיבור נקבע על פי מספר הצמתים שהוא מכיל. רכיב חיבור עם צומת אחד בלבד הוא הרכיב הקטן ביותר האפשרי.
• סריקה traversal וחיפוש: רכיבי החיבור מזוהים לעתים קרובות באמצעות אלגוריתמי סריקה של גרף כדוגמת אלגוריתם חיפוש לעומק (DFS). אלגוריתמים אלה עוזרים לחקור את הגרף ולזהות קבוצות של צמתים מחוברים.
• יישומים: לרכיבי חיבור יש יישומים שונים, כולל גילוי קהילות ברשתות חברתיות, עיבוד תמונות, מציאת אשכולות בנתונים ופתרון בעיות הקשורות לרשת.

לסיכום, גרפים עשויים מרכיבי חיבור, המייצגים את תת-הגרפים המחוברים בתוך הגרף הגדול יותר. זיהוי והבנת רכיבים אלה חיוני בתחומים שונים בתורת הגרפים.

אתגר: מציאת רכיבי חיבור connected components בגרף לא-מכוון

תיאור:

נותנים לך גרף לא-מכוון המיוצג כרשימת סמיכויות adjacency list. המשימה היא לכתוב פונקציה המחזירה רשימה של רכיבי חיבור מן הגרף. כל רכיב חיבור הוא רשימה של צמתים המייצגים את כל הצמתים ברכיב יחיד בסדר שבו הם נסרקו.

אתה יכול להעזר בפונקציה הבאה לצורך פיתוח הפתרון:

def find_connected_components(graph: dict) -> List[List[str]]:
    pass

קלט:

• graph: רשימת סמיכויות המייצגת גרף. רשימת הסמיכויות הינה מילון כאשר המפתחות הם צמתים בגרף (מיוצגים כמחרוזות), והערכים המתאימים הם רשימות של מחרוזות המייצגות את השכנים של כל צומת.

פלט:

• רשימה של רשימות כאשר כל רשימה פנימית מייצגת רכיב חיבור אחר בגרף.

הערות:

• הגרף עשוי להכיל רכיבי חיבור מרובים.
• הסדר שבו אתה מוצא את הרכיבים או את הצמתים בתוך כל רכיב אינו משנה.

דוגמה:

graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E'],
    'G': ['H'],
    'H': ['G']
}


result = find_connected_components(graph)


# Output:
# result = [['A', 'B', 'C', 'D', 'E', 'F'], ['G', 'H']]

הסבר:

בדוגמה לעיל, הגרף מכיל שני רכיבי חיבור:

['A', 'B', 'C', 'D', 'E', 'F']
['G', 'H']

כל רכיב מייצג קבוצה של צמתים המחוברים זה לזה באמצעות נתיב אחד. הפונקציה מחזירה את רכיבי החיבור הללו כרשימות נפרדות בתוך הרשימה אותה היא מחזירה.

פתרון:

הפונקציה find_connected_components() משתמשת באלגוריתם חיפוש לעומק DFS כדי למצוא ולהחזיר את כל הרכיבים מהם מורכב הגרף שהיא מקבלת כקלט.

from typing import List

def find_connected_components(graph: dict) -> List[List[str]]:
    # List of lists each representing a component
    components = []
    
    # Set to keep track of visited nodes during DFS
    visited = set()
    
    def dfs(start):
        # List to store the current component
        component = []
        
        visited.add(start)
        
        # Using stack to do an iterative DFS
        stack = [start]
        
        while stack:
            current = stack.pop()
            component.append(current)
            
            # Explore neighbors of the current node
            for neighbor in graph[current]:
                if neighbor not in visited:
                    visited.add(neighbor)
                    stack.append(neighbor)
        components.append(component)
        
    # Iterate through all nodes in the graph to explore each connected component 
    for node in graph:
        if node not in visited:
            # Call DFS starting from the unvisited node to explore its connected component
            dfs(node)
    
    return components

נבדוק:

# Test cases

graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E'],
    'G': ['H'],
    'H': ['G']
}

result = find_connected_components(graph)
print(result)
# Output: [['A', 'C', 'F', 'E', 'B', 'D'], ['G', 'H']]


graph_disjoint = {
    'A': ['B', 'C'],
    'B': ['A'],
    'C': ['A'],
    'D': ['E'],
    'E': ['D']
}

result_disjoint = find_connected_components(graph_disjoint)
print(result_disjoint)
# Output: [['A', 'B', 'C'], ['D', 'E']]


graph_single_component = {
    'A': ['B'],
    'B': ['C', 'D'],
    'C': [],
    'D': [],
}

result_single_component = find_connected_components(graph_single_component)
print(result_single_component)
# Output: [['A', 'B', 'D', 'C']]


graph_single_node = {
    'A': []
}

result_single_node = find_connected_components(graph_single_node)
print(result_single_node)
# Output: [['A']]

נסביר:

הפונקציה `find_connected_components` נועדה לזהות ולהחזיר רשימה של רכיבי חיבור בתוך גרף לא מכוון המיוצג על ידי רשימת סמיכות.

1. אתחול:

   • `components`: רשימה לאחסון רכיבי החיבור. כל רכיב מיוצג ע"י רשימה של צמתים.
   • `visited`: סט למעקב אחר צמתים בהם ביקרה הפונקציה במהלך סריקת DFS.

2. לולאה עוברת על כל צמתי הגרף וכל צומת, אם טרם ביקרה בו הפונקציה מועבר להמשך טיפול בפונקציה הפנימית `dfs` שסורקת את הגרף במטרה למצוא רכיב חיבור יחיד.

3. פונקציה פנימית (`dfs`):

   • מקבלת צומת ממנו מתחילה הסריקה (`start`) כארגומנט.
   • מאתחלת רשימה ריקה (`component`) לאחסון רכיב החיבור הנוכחי.
   • הפונקציה מוסיפה את צומת ההתחלה (`start`) לסט `visited`.
   • משתמשת ב-stack כדי לבצע סריקת DFS איטרטיבית:
     • שולפת צמתים מתוך ה-stack ומוסיפה אותם לסט `component`.
     • חוקרת שכנים של הצומת הנוכחי במידה ומוצאת שכן שטרם ביקרה בו, הוא מתווסף לסט `visited` ומצורף ל-stack להמשך סריקה.
     • מוסיפה את רשימת רכיבי החיבור הנוכחית `component` לרשימת כל רכיבי החיבור `components` אותה הפונקציה תחזיר בסופו של דבר.

לסיכום, הפונקציה משתמשת בחיפוש לעומק כדי לחקור את רכיבי החיבור של גרף. היא מתחילה מצמתים שלא ביקרו בהם, חוקרת את רכיבי החיבור שלהם וממשיכה עד לביקור בכל הצמתים. לאחר מכן, הרכיבים שזוהו מוחזרים כרשימה של רשימות.

אתגר: מציאת כל הנתיבים בין שני צמתים בגרף

תיאור האתגר:

נתון גרף לא מכוון המיוצג באמצעות רשימת סמיכויות. המשימה היא למצוא את כל הנתיבים האפשריים בין שני צמתים נתונים, start ו-end.

תבנית הפונקציה:

def find_all_paths(graph: dict, start: str, end: str) -> List[List[str]]:
    pass

הפונקציה מקבלת את הקלטים הבאים:

• graph - מיוצג באמצעות רשימת סמיכויות adjacency list
• start - צומת המקור ממנו יצאו הנתיבים
• end - צומת היעד אליו צריכים להגיע הנתיבים

פלט הפונקציה:

הפונקציה תחזיר רשימה של רשימות, כאשר כל רשימה פנימית מייצגת נתיב מצומת המקור לצומת היעד. כל נתיב צריך להיות מיוצג כמערך שמות הצמתים המסודרים לפי סדר הימצאותם בנתיב.

דוגמה:

graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F', 'G'],
    'D': [],
    'E': ['F'],
    'F': ['A'],
    'G': ['B']
}

start_node = 'A'
end_node = 'F'
result = find_all_paths(graph, start_node, end_node)

# Output:
# result = [['A', 'C', 'G', 'B', 'E', 'F'], ['A', 'C', 'F'], ['A', 'B', 'E', 'F']]

• הפונקציה קיבלה ייצוג של גרף באמצעות רשימת סמיכויות ואת צומת המקור וצומת היעד בתור קלטים והחזירה רשימה של רשימות הכוללת 2 נתיבים המחברים בין המקור והיעד.

הערות:

• כל הנתיבים בפלט הפונקציה צריכים להיות ייחודיים (ללא נתיבים כפולים).
• אם הפונקציה לא מצאה נתיב בין המקור ליעד יש להחזיר רשימה ריקה.

פתרון אפשרי:

הפונקציה find_all_paths() מיועדת למצוא את כל הנתיבים האפשריים בין שני צמתים נתונים, start ו-end, בגרף לא מכוון המיוצג באמצעות רשימת סמיכויות (adjacency list). לצורך כך היא משתמשת באלגוריתם חיפוש לעומק DFS.

from collections import deque

def find_all_paths(graph, start, end):
    # Store all the paths in a list of lists
    paths = []

    # Stack to track which node and path to handle in each iteration
    path = [start]
    stack = deque()
    stack.append((start, path))
    
    while stack:
        # Remove the last node and its corresponding path
        current_node, path = stack.pop()
        
        # If the current_node is the destination, 
        #  add the path to the paths list and continue
        if current_node == end:
            paths.append(path)
            continue
        
        # For each neighbor of the current_node, if it is not in the current path,
        # extend the current path with the neighbor and add it to the stack for further exploration
        for neighbor in graph[current_node]:
            # If neighbor not in path it can be visited
            if neighbor not in path:
                # Add to path list or create if None
                current_path = path + [neighbor]
                # Add the neighbor and its updates path to the stack
                stack.append((neighbor, current_path))

    return paths

נסביר:

1. הפונקציה מתחילה על ידי יצירת רשימה ריקה paths לאחסון כל הנתיבים הנמצאים בין הצמתים start ו-end.
2. מבנה נתונים ערימה stack נוצר כדי לעקוב אחר צמתים ונתיביהם המתאימים במהלך סקירת הגרף. הוא מאותחל עם הצומת start ונתיביו, המיוצגים כטאפל Tuple(start, [start]).
3. השימוש ב-deque מהווה כלי קיבול יעיל לא פחות מרשימה של פייתון לניהול stack. בגלל האופן שבו עובדת רשימה של פייתון השימוש ב-deque כ- stack לא מעלה או מוריד מיעילות הוספת והסרת הפריטים מהערימה הנעשית בסיבוכיות זמן קבועה O(1) בכל מקרה. בחרתי להשתמש ב-deque כדי להציג ללומד אופן נפוץ של כתיבת stack אליו צריך להתרגל.
4. לולאת while היא שמבצעת את הסקירה והיא תמשיך לרוץ כל עוד יש צמתים בערימה stack אותם יש לסרוק.
5. בתוך הלולאה, הפונקציה מסירה את הצומת האחרון מראש הערימה stack. הצומת מאוחסן ב-current_node, והנתיב מאוחסן ב-path.
6. אם current_node הוא זהה לצומת end, זה אומר שנמצא נתיב מ-start ל-end. במקרה זה, הנתיב מתווסף לרשימת paths, והלולאה ממשיכה לסרוק צמתים ונתיבים נוספים.
7. אם current_node אינו הצומת end, הפונקציה עוברת על כל שכניו של הצומת current_node בגרף.
8. עבור כל שכן, הפונקציה בודקת אם הוא אינו נמצא כבר בנתיב path. אם הוא לא נמצא בנתיב, זה אומר שהשכן יכול להיות חלק מהנתיב הנסרק.
9. השכן מתווסף אז לנתיב הנוכחי כדי ליצור נתיב חדש (current_path).
10. הנתיב החדש והשכן מתווספים לערימה stack לסריקה נוספת בפעמים הבאות.
11. התהליך נמשך עד שכל הנתיבים האפשריים בין הצמתים start ו-end נסרקו.
12. לבסוף, הפונקציה מחזירה את רשימת כל הנתיבים שנמצאים בין הצמתים start ו-end, המאוחסנים ברשימה paths.

הערה: הפונקציה משתמשת באלגוריתם חיפוש לעומק (DFS) כדי לסרוק את כל הנתיבים האפשריים בגרף, והיא יעילה בהתמודדות עם הפניות מעגליות ונתיבים מרובים בין צמתים.

הקוד הבא בוחן את הפונקציה find_all_paths():

# Test cases

# Simple graph
graph = {
'A': ['B', 'C'],
'B': ['C', 'D'],
'C': ['D'],
'D': []
}

# Test simple graph
paths = find_all_paths(graph, 'A', 'D')
print(paths)
# output = [
# ['A', 'C', 'D'], 
# ['A', 'B', 'D'], 
# ['A', 'B', 'C', 'D']
# ]

graph = {
'A': ['B', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F'],
'D': ['B'],
'E': ['B', 'F'],
'F': ['C', 'E']
}

paths = find_all_paths(graph, 'A', 'F')
print(paths)
# output = [
# ['A', 'C', 'F'],
# ['A', 'B', 'E', 'F']
# ]

# Cyclic graph
graph_cyclic = {
'A': ['B', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F'],
'D': ['B'],
'E': ['B', 'F'],
'F': ['C', 'E']
}

# Test cyclic graph
paths = find_all_paths(graph_cyclic, 'A', 'F')
print(paths)
# output = [
# ['A', 'C', 'F'],
# ['A', 'B', 'E', 'F']
# ]

paths = find_all_paths(graph, 'A', 'B')
print(paths)
# output = [
# ['A', 'C', 'F'],
# ['A', 'B', 'E', 'F']
# ]

# Start and end node are the same
paths = find_all_paths(graph, 'B', 'B')
print(paths)
# output = ['B']

# End node not in graph
paths = find_all_paths(graph, 'B', 'N')
print(paths)
# output = []

איתור הפניות מעגליות Cycles בגרף

מעגל cycle המצוי בגרף הוא נתיב סגור, כאשר נתיב הוא רצף של צמתים (קודקודים) המחוברים באמצעות קשתות. מעגל הוא סוג מסוים של נתיב שמתחיל ומסתיים באותו צומת תוך כדי מעבר דרך צמתים אחרים באמצע. כאשר הוא אינו חוזר על אף צומת ביניים (למעט הצומת ההתחלתי והסופי).

הרצף הבא מייצג מעגל בגרף: "v1 → v2 → v3 → ... → vn → v1", כאשר "v" מייצג צומת ו"→" מייצג קשת המחברת צמתים סמוכים. נוכחות של מעגל בגרף יוצרת לולאה בתוך מבנה הגרף.

ניתן לגלות מעגל בגרף לא-מכוון ביעילות באמצעות אלגוריתם חיפוש לעומק (DFS). במהלך סריקת DFS של גרף, נבדוק את קיומו של מעגל על ידי מעקב אחר הצמתים והוריהם.

הרעיון העיקרי מאחורי מציאת מעגל בגרף לא-מכוון באמצעות DFS מבוסס על back edge - קשת המחברת צומת לאחד מהוריו הלא ישירים. אם נתקל ב-back edge במהלך סריקת DFS, נסיק את קיומו של מעגל בגרף.

איתור הפניות מעגליות בגרף cycle detection חשוב למגוון תחומים ויישומים:

• במדעי המחשב, גילוי מעגלים משמש לגילוי ומניעת חסימות deadlock. חסימה מתרחשת כאשר תהליכים תלויים אחד בשני באופן מעגלי ומכיוון שכל תהליך חייב את משנהו המערכת לא תוכל לעבוד.
• ברשתות חברתיות, זיהוי הפניות מעגליות עשוי לשמש לזיהוי קבוצות של אנשים קשורים. מה שיכול לסייע ביצירת קהילות וירטואליות.
• בביולוגיה חישובית, גילוי הפניות מעגליות יכול לשמש לזיהוי גנים המעורבים באותו מסלול ביולוגי.
• בשינוע לוגיסטי, גילוי מחזורים יכול לשמש לזיהוי מסלולי משלוח הגורמים לרכב לנסוע במעגלים מה שגורם לבזבוז משאבים.

בכל המקרים המוזכרים, גילוי הפניות מעגליות יכול לעזור לנו להבין טוב יותר את המבנה של המערכת שאנחנו עובדים עליה כי הוא מאפשר לנו לזהות קבוצות של דברים הקשורים זה לזה, או לזהות מסלולים שעשויים להיות חסכוניים ויעילים יותר.

אתגר: מציאת מעגל בגרף לא-מכוון

נתון גרף לא-מכוון המיוצג כרשימת סמיכויות adjacency list. האתגר שלך הוא ליישם פונקציה has_cycle() המקבלת ייצוג של גרף כקלט ובודקת אם הגרף מכיל הפנייה מעגלית. הפונקציה צריכה להחזיר True אם הגרף מכיל הפנייה מעגלית ו-False אחרת.

מבנה הפונקציה:

def has_cycle(graph: dict, start: str) -> bool:
    pass

קלט הפונקציה:

graph: מילון שהוא adjacency list המייצג גרף לא-מכוון. המפתחות הם צמתים בגרף (מיוצגים כמחרוזות), והערכים המתאימים הם רשימות של מחרוזות המייצגות את השכנים של כל צומת.

פלט הפונקציה:

הפונקציה מחזירה ערך בוליאני, True אם הגרף מכיל ולו מעגל אחד, ו-False אם הגרף הוא א-מעגלי (אינו מכיל מעגלים).

הערה:

הגרף יכול להכיל רכיבי חיבור מרובים, כאשר צריך לטפל באופן עצמאי בכל רכיב חיבור במטרה לגלות האם באחד מהם ישנו מעגל.

לדוגמה:

graph1 = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}


graph2 = {
    'A': ['B', 'C'],
    'B': ['A', 'D'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': [],
    'F': ['C']
}


assert has_cycle(graph1, 'A') == True
assert has_cycle(graph2, 'A') == False

print("All tests passed!")

הסבר:

• בדוגמה הראשונה (graph1), הגרף מכיל מעגלים. למשל, הנתיב A -> B -> E -> F -> C -> A יוצר מעגל.
• בדוגמה השנייה (graph2), הגרף א-מעגלי. למרות שיש לו רכיבי חיבור מרובים, אף אחד מהרכיבים אינו מכיל מעגלים.

אילוצים:

בגרף הקלט לא קיימים צמתים המקשרים לעצמם (self-loops).

הפיתרון כרוך במימוש שני צעדים.

קודם כל, פתרון חלקי למציאת מעגל בגרף יחיד:

האתגר מזכיר את הצורך לזהות את כל מרכיבי הגרף גם אם הוא מחולק לקומפננטות. נתחיל בפתרון של בעיה פחות סבוכה שהיא כיצד לאתר הפניה מעגלית בגרף יחיד. אחר כך נעלה את דרגת הסיבוכיות של הפתרון כדי להתמודד עם גרף המכיל מספר רכיבים.

הפונקציה has_cycle() היא מימוש רקורסיבי של אלגוריתם חיפוש לעומק (DFS) לצורך זיהוי הפניות מעגליות בגרף:

def has_cycle(graph, start_node, parent=None, visited=None):
    if not visited:
        visited = set()
    visited.add(start_node)
    # Check each neighbor of the current node
    for neighbor in graph[start_node]:
        # If neighbor is visited and not the parent, a back edge is found, indicating a cycle
        if neighbor in visited and parent != neighbor: 
            return True
        if neighbor not in visited: 
            # If neighbor is not visited, recursively check its subgraph
            util_has_cycle(neighbor, start_node)
            
    return False

נסביר:

1. `def has_cycle()`: היא פונקציה רקורסיבית שבודקת אם קיימת הפנייה מחזורית בגרף הלא מכוון graph אותו מייצג adjacency list כאשר נקודת המוצא היא הצומת `start_node` . הפרמטר `parent` מציין את הצומת ההורה של תת הגרף בו מטפלת הפונקציה. הפרמטר `visited` מאחסן את סט הצמתים שנסרקו במסגרת ה-DFS.

2. if not visited:
       visited = set()
   visited.add(start_node)

   אם קבוצת הצמתים שכבר נבדקו (`visited`) לא סופקה (כלומר, היא `None`), הפונקציה מאתחלת סט ריק שנקרא `visited`. אנחנו לא מעבירים את הסט כפרמטר אילא יוצרים בתוך הפונקציה במידה ואינו קיים כדי למנוע באגים.

   בהמשך, הצומת `start_node` מצורף לסט visited כדי למנוע ביקור נוסף בו בהמשך.

3. לולאת for עוברת על כל השכנים של ההורה בגרף. בתוך הלולאה:

   • התנאי:

     if neighbor in visited and parent != neighbor

     אומר שאם השכן כבר נסרק (visited) והוא אינו ההורה של הצומת הנוכחי אז אפשר להסיק שיש back edge ולפיכך הגרף מכיל מחזור. אם מתקיים התנאי הפונקציה תחזיר True כי קיימת הפנייה מעגלית בגרף.

   • אם לא מתקיים התנאי, אז בודקים אם השכן אינו צומת שכבר נסרק (visited):

     if neighbor not in visited

     אם מתקיים התנאי יש צורך לסרוק את תת הגרף ולשם כך מתבצעת קריאה רקורסיבית לפונקציה `has_cycle()` עם ה- `start_node` כהורה והשכן neighbor בתור נקודת המוצא לסריקה.

     if neighbor not in visited:
         # If neighbor is not visited, recursively check its subgraph
         util_has_cycle(neighbor, start_node)

4. אחרי שהפונקציה מסיימת במידה ולא נמצאו הפניות מעגליות בתת-הגרף של הצומת שמקורו ב-`start_node`, הפונקציה תחזיר `False`.

שים לב: הפונקציה לא יודעת לטפל בגרף הכולל מספר רכיבים disconnected graph היות והיא מסוגלת לסרוק רכיב אחד החל מצומת המוצא start_node שהיא מקבלת כפרמטר.

הקוד הבא בוחן את הפונקציה has_cycle():

graph1 = {
'A': ['B', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F'],
'D': ['B'],
'E': ['B', 'F'],
'F': ['C', 'E']
}

graph2 = {
'A': ['B', 'C'],
'B': ['A', 'D'],
'C': ['A', 'F'],
'D': ['B'],
'E': [],
'F': ['C']
}

# assert has_cycle(graph1, 'A') == True
res1 = has_cycle(graph1)
print(res1)

# assert has_cycle(graph2, 'A') == False
res2 = has_cycle(graph2)
print(res2)

אחרי שראינו כיצד לבדוק קיום הפניות מעגליות בגרף הכולל רכיב חיבור אחד, ניישם את הפונקציה על גרף העשוי לכלול מספר רכיבי חיבור. לשם כך, נעבור בתוך לולאה באופן שיטתי על הצמתים המרכיבים את הגרף ונעביר כל אחד מהם לבחינה בפונקציה util_has_cycle() שעושה את מה שהפונקציה-has_cycle() לעיל עשתה - מזהה אם ישנו מעגל בתת הגרף שהועבר לו ומחזירה ערך בוליאני בהתאם:

def has_cycle(graph: dict) -> bool:
    # Set to keep track of visited nodes during DFS
    visited = set()

    def util_has_cycle(start_node, parent_node):
        # Mark the current node as visited
        visited.add(start_node)

        # Check each neighbor of the current node
        for neighbor in graph[start_node]:
            # If neighbor is visited and not the parent, a back edge is found, indicating a cycle
            if neighbor in visited and parent_node != neighbor: 
                return True
            if neighbor not in visited: 
                # If neighbor is not visited, recursively check its subgraph
                util_has_cycle(neighbor, start_node)

        return False

    # Iterate through all nodes in the graph to explore each connected component 
    for node in graph:
        if node not in visited:
            # Call DFS starting from the unvisited node to explore its connected component
            if util_has_cycle(node, None):
                return True

    # If no cycles are found in any connected component, return False
    return False

• הפונקציה has_cycle() יודעת לטפל בגרפים המכילים מספר רכיבים disconnected graphs תוך שהיא בודקת אם קיימות הפניות מעגליות בכל אחד מרכיבי החיבור של גרף הקלט.

נסביר:

• לולאת for עוברת על רכיבי הגרף באופן שיטתי ומעבירה אותם לאיתור הפניות מעגליות בפונקציה הפנימית util_has_cycle():

  # Iterate through all nodes in the graph to explore each connected component
  for node in graph:
      if node not in visited:
          # Call DFS starting from the unvisited node to explore its connected component
          if util_has_cycle(node, None):
              return True

• התנאי:

  if node not in visited

  בודק אם צומת טרם נסרק מה שאומר שהוא שייך לרכיב פונקציה נפרד. אחנו קוראים לפונקציה הפנימית `util_has_cycle()` המתחילה לסרוק אחר הפניה מעגלית עבור צמתים אילה. אם הפונקציה `util_has_cycle()` מחזירה `True` זה אומר שנמצא מעגל והפונקציה הראשית תחזיר `True` באופן מיידי אבל אם לא נמצאו מעגלים באף רכיב, הפונקציה תגיע לסופה ותחזיר `False`.

אתגר: מציאת מספר איים בגרף

תיאור האתגר:

נתונה תבנית דו-ממדית (=רשת) הכוללת קואורדינטות משני סוגים: 1 (יבשה) ו-0 (מים). עליך לספור את מספר האיים כאשר אי מוקף במים והוא נוצר על ידי חיבור גושי יבשה הסמוכים זה לזה באופן אופקי או אנכי (ולא באלכסון).

לצורך הפתרון אתה יכול להשתמש בפונקציה הבאה:

def count_islands(grid: List[List[int]]) -> int:
    # Your code here

בוא נראה כמה דוגמאות:

• הרשת הבאה אינה כוללת איים (כל הקואורדינטות מסומנות 0):

  grid = [
      [0, 0],
      [0, 0],
  ]

• הרשת הבאה כוללת אי 1:

  grid = [
      [0, 0],
      [0, 1],
  ]

• ברשת זו 2 איים:

  grid = [
      [1, 0],
      [0, 1],
  ]

  שים לב! אי נוצר מחיבור גושי יבשה הסמוכים זה לזה באופן אופקי או אנכי ולא באלכסון.

• גם ברשת זו 2 איים:

  grid = [
      [1, 0, 1],
      [0, 1, 1],
  ]

• ברשת זו 3 איים:

  grid = [
      [1, 1, 0, 0, 0],
      [0, 1, 0, 0, 0],
      [0, 0, 1, 0, 1],
      [0, 0, 0, 1, 1]
  ]

• ברשת זו אי 1 בודד:

  grid = [
      [1, 1, 1, 1, 0],
      [1, 1, 0, 1, 0],
      [1, 1, 0, 0, 0],
      [0, 0, 0, 0, 0]
  ]

רוצה רמזים לפתרון? בבקשה:

• איך אתה יכול לעבור על כל הרשת בלי להחמיץ קואורדינטות?
• איזה סוג traversal ייתן לך את התוצאה הטובה ביותר (BFS או DFS)?
• איך לאתר ולסמן את השכנים של כל נקודה המזוהה כיבשה?

פתרון אפשרי:

הפונקציה count_islands() תקבל את הרשת grid כפרמטר ותחזיר את מספר האיים ברשת שהיא תמנה באמצעות משתנה מספרי islands_counter:

def count_islands(grid):
    """Counts the number of islands in the grid."""
    islands_counter = 0
    # Do something to count the islands
    return islands_counter

כדי לבקר בכל קואורדינטה ברשת הפונקציה תשתמש בלולאה בתוך לולאה. הלולאה החיצונית עוברת על כל השורות מלמעלה למטה והפנימית רצה בתוכה ועוברת על כל התאים בכל שורה:

def count_islands(grid):
    """Counts the number of islands in the grid."""
    islands_counter = 0
    
    # Validate
    if not grid or not grid[0]: return islands_counter


    num_rows = len(grid)
    num_cols = len(grid[0])


    for y in range(num_rows):
        for x in range(num_cols):
            pass
    
    return islands_counter

אם הערך של קואורדינטה מסוימת הוא 1 מה שמעיד על יבשה חדשה אז תוסיף 1 למונה האיים islands_counter וגם תעביר את הקואורדינטה לפונקציה אחרת mark_visited() כדי שתסמן את הקואורדינטה כמי שביקרנו בה:

def count_islands(grid):
    """Counts the number of islands in the grid."""
    islands_counter = 0

    # Validate
    if not grid or not grid[0]: return islands_counter

    num_rows = len(grid)
    num_cols = len(grid[0])


    for y in range(num_rows):
        for x in range(num_cols):
            # On meeting a new unexplored land mass (marked 1) add 1 to islands_counter
            # And mark the coordinate and its neighbors as visited (marked with 2)
            if grid[y][x] == 1:
                islands_counter += 1
                mark_visited(grid, x, y, num_rows, num_cols)


    return islands_counter

נוסיף את הפונקציה mark_visited() שתקבל את הקואורדינטה בה ביקרנו ותשנה את הערך שלה מ-1 ל-2 במטרה לסמן שביקרנו את הקואורדינטה ועל כן היא אינה יכולה להיחשב כיבשה שטרם נחקרה (כי יבשה שטרם נחקרה מזוהה על ידי הספרה 1). בנוסף, הפונקציה תסקור את השכנים (למעלה ולמטה, שמאל וימין) ותסמן גם אותם, אם הם יבשה, ב-2:

def mark_visited(grid, x, y, num_rows, num_cols): 
    """Marks the current coordinate and its neighbors as visited.""" 
    adjacent_cells = [ 
        (0, 0), # current coordinate 
        (-1, 0), 
        (1, 0), # horizontal neighbors 
        (0, -1), 
        (0, 1), # vertical neighbors
    ] 
    # Stack to track the nodes for implementing a DFS traversal 
    stack = [(x, y)] 
    while stack: 
        # Pop from the top
        x, y = stack.pop() 
        for dx, dy in adjacent_cells: 
            # Make sure coordinate doesn't exceed the grid 
            if 0 <= y + dy < num_rows and 0 <= x + dx < num_cols and grid[y + dy][x + dx] == 1: 
                # Mark coordinate as visited 
                grid[y + dy][x + dx] = 2 
                # Add on top
                stack.append((x + dx, y + dy))

נסביר:

• הסקירה traversal של השכנים נעשית על פי סדר של DFS כפי שמעיד השימוש ב-stack בפונקציה.
• המשתנה adjacent_cells מגדיר את הקואורדינטות היחסיות של התא הנוכחי ושל שכניו. סריקת DFS מתחילה מהתא הנוכחי, והיא בודקת את ארבעת שכניו (למעלה, למטה, שמאל, ימין).

לבחינת הקוד שכתבנו:

# Example grids to test the function
grid1 = [
    [1, 1, 0, 0, 0],
    [0, 1, 0, 0, 0],
    [0, 0, 1, 0, 1],
    [0, 0, 0, 1, 1]
]

grid2 = [
    [1, 1, 1, 1, 0],
    [1, 1, 0, 1, 0],
    [1, 1, 0, 0, 0],
    [0, 0, 0, 0, 0]
]

grid3 = [
    [1, 0, 1],
    [0, 1, 1],
]

grid4 = [
    [0, 0],
    [0, 1],
]

grid5 = [
    [0, 0],
    [0, 0],
]

# Testing the function with example grids
number_of_islands1 = count_islands(grid1)
print(number_of_islands1)  # Output: 3

number_of_islands2 = count_islands(grid2)
print(number_of_islands2)  # Output: 1

number_of_islands3 = count_islands(grid3)
print(number_of_islands3)  # Output: 2

number_of_islands4 = count_islands(grid4)
print(number_of_islands4)  # Output: 1

number_of_islands5 = count_islands(grid5)
print(number_of_islands5)  # Output: 0

• אפשר לפתור את הבעיה של סקירת השכנים בפונקציה mark_visited() באמצעות DFS סריקה לעומק או BFS סריקה לרוחב. פה השתמשנו ב-DFS.

סיכום

חיפוש לעומק (DFS) הוא אלגוריתם בסיסי ופופולרי לסריקה של גרפים. הוא מתחיל מצומת מוצא וסורק רחוק ככל האפשר לאורך ענף עד סופו לפני שהוא חוזר backtrack וממשיך לחפש בנתיב אחר שטרם נסרק. מכאן השם "חיפוש לעומק". כדי לעקוב אחר הצמתים הנסרקים DFS משתמש במבנה נתונים ערימה stack או ברקורסיה. משתמשים ב-DFS, בין השאר, כדי למצוא את כל הנתיבים המחברים בין שני צמתים או כדי לקבוע האם צמתים שייכים לאותו הגרף, לגלות הפניות מעגליות בגרף, ולמצוא את כל הרכיבים מהם מורכב גרף. סיבוכיות הזמן של DFS היא O(V + E), כאשר V הוא מספר הצמתים ו-E הוא מספר הקשתות. סיבוכיות המקום הנדרשת היא O(V). במילים פשוטות, הזמן והמקום הדרושים לביצוע DFS גדלים באופן לינארי עם גידול מספר הקשתות והצמתים בגרף.

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

יישום תורת הגרפים בפייתון - חלק א

יישום רשימת סמיכויות adjacency list - חלק ב בסדרה על גרפים

מיון טופולוגי באמצעות אלגוריתם Kahn

stacks, ערימות וחידות

General Tree data structure עץ נתונים

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים