המדריך התמציתי ליישום עץ בינארי בפייתון

עצים בינאריים הם דרך גמישה לייצוג קשרים בין אובייקטים, כאשר עצי חיפוש בינאריים מספקים יכולות חיפוש ומיון יעילות. במדריך זה, נלמד את היסודות של עצים בינאריים ועצי חיפוש בינאריים, ונראה כיצד ליישם ולעבוד איתם באמצעות Python. מדריך זה הוא המשך של המדריך הקודם שעסק בעץ נתונים כללי שם ישנו הסבר על מבנה הנתונים עץ, טבעו הרקורסיבי וקוד פייתון ליישום.

עץ בינארי binary tree הוא מבנה נתונים המורכב מצמתים nodes, כאשר לכל צומת יש לכל היותר שני ילדים, ילד שמאלי וילד ימני. העץ מתחיל מצומת הנקרא שורש root, ולכל צומת יכולים להיות אפס, אחד או שני ילדים.

נראה דוגמה לעץ בינארי:

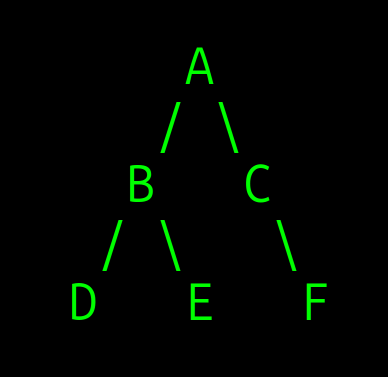
• בעץ זה, הצומת "A" הוא שורש העץ, ויש לו שני ילדים: "B" ו-"C". לצומת "B" יש שני ילדים: "D" ו-"E". לצומת "C" יש ילד אחד "F". צמתים "D", E" ו-"F" מכונים צמתים עלים leaf nodes כי אין להם ילדים.

עץ חיפוש בינארי (BST) הוא סוג של עץ בינארי שיש לו את "תכונת העץ הבינארי" Binary Search Tree Invariant - עבור כל צומת בעץ, כל הצמתים בתת-העץ השמאלי הם בעלי ערכים הנמוכים מערכו, וכל הצמתים בתת-העץ הימני מכילים ערכים גדולים מערכו. מאפיין זה הופך את עצי החיפוש הבינאריים לשימושיים כשרוצים לחפש או לאחזר מידע.

זו דוגמה לעץ חיפוש בינארי BST:

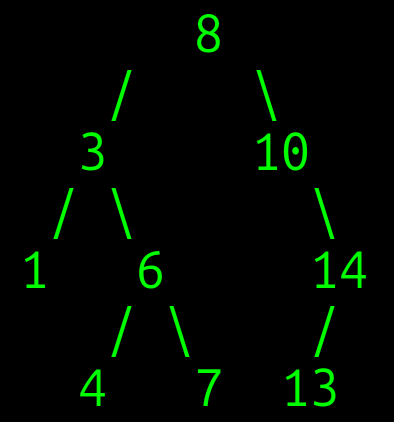
• בעץ המוצג לעיל אפשר לראות את תכונת עץ החיפוש הבינארי בפעולה. לדוגמה, משמאל לצומת 3 אפשר לראות רק ערכים נמוכים ממנו (במקרה זה ערך 1 בלבד), ומימין ערכים גבוהים ממנו (4, 6, 7).

תכונת עץ החיפוש הבינארי BST invariant מאפשרת חיפוש, הכנסה ומחיקה יעילות. על ידי השוואת הערך אותו מחפשים לערך הצומת הנוכחי ומעבר לילד השמאלי (אם הערך אותו מבקשים נמוך מערך הצומת הנוכחי) או הימני (אם הערך גבוה יותר) מרחב החיפוש מצטמצם למעשה בחצי בכל שלב. כתוצאה מכך, סיבוכיות הזמן של פעולות אלו היא לוגריתמית, מסומנת כ-O(log N). תכונה זו מקנה לעצים בינאריים חשיבות רבה במגוון יישומים כדוגמת: מסדי נתונים, ארגון מערכות קבצים באופן היררכי, מהדרים (קומפיילרים), השלמה אוטומטית, ועוד.

יישום עץ בינארי בשפת פייתון

עץ נתונים מורכב מצמתים nodes. כל node צומת הוא עץ בפני עצמו. נקרא לקלאס פייתון המייצג צומת אחד בשם BST:

class BST:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

• הקלאס BST כולל את השדות והמתודות של צומת בעץ חיפוש בינארי. צומת שהוא גם עץ (למה? רקורסיה . צריך להתרגל 😄).

• המתודה המיוחדת __init__() מאתחלת אובייקטים מן הקלאס. היא כוללת את השדות:

  1. data - המידע המוכל בצומת. זה יכול להיות מחרוזת, מספר, אובייקט או מה שצריך.
  2. left - הילד השמאלי של הצומת הנוכחי. מאותחל עם ערך None כי ברירת המחדל היא שאין צומת שמאלי.
  3. right - הילד הימני של הצומת הנוכחי. ערכו ההתחלתי None.

נוסיף לקלאס BST מתודה insert() להוספת צמתים לעץ תוך שמירה על תכונת עץ החיפוש הבינארי - מידע קטן יותר ילך לתת העץ השמאלי וגדול יותר לימיני:

def insert(self, data):
    if data == self.data:
        return  # Binary tree can't have duplicate data
        
    if data < self.data:
        # Add data in the left subtree
        if self.left:
            # The node has a left subtree
            # Recursively add data to the left subtree
            self.left.insert(data)
        else:
            # The left subtree is empty
            # Add a new node with the given data as the left child
            self.left = BST(data)
    else:
        # Add data in the right subtree
        if self.right:
            # The node has a right subtree
            # Recursively add data to the right subtree
            self.right.insert(data)
        else:
            # The right subtree is empty
            # Add a new node with the given data as the right child
            self.right = BST(data)

נסביר את המתודה insert():

• המתודה insert() לוקחת פרמטר `data`, המייצג את הערך שיש להוסיף לעץ החיפוש הבינארי.
• אם הערך `data` שווה לנתוני הצומת הנוכחי (`self.data`), המתודה מחזירה מיד מכיוון שלעץ בינארי לא יכולים להיות ערכים כפולים.

• אם הערך data קטן מערכו של הצומת הנוכחי ('self.data'), המתודה עוברת אל תת העץ השמאלי.

  • אם לצומת הנוכחי יש ילד שמאלי (`self.left` אינו `None`), המתודה קוראת רקורסיבית ל-`insert()` בילד השמאלי, ואז סורקת במורד תת-העץ השמאלי כדי למצוא את המיקום המתאים להוספת הערך.
  • אם לצומת הנוכחי אין ילד שמאלי (`self.left` הוא `None`), נוצר צומת חדש עם הערך, ומוקצה כילד השמאלי של הצומת הנוכחי.

• אם הערך data גדול מערכו של הצומת הנוכחי ('self.data'), המתודה עוברת אל תת העץ הימיני.

  • אם לצומת הנוכחי יש ילד ימני (`self.right` אינו `None`), המתודה קוראת רקורסיבית ל- `insert()` על הילד הימני, ולמעשה סורקת במורד בתת העץ הימני כדי למצוא את המיקום המתאים להוספת הערך .
  • אם לצומת הנוכחי אין ילד ימני (`self.right` הוא `None`), צומת חדש עם הערך data נוצר ומוקצה כילד הימני של הצומת הנוכחי.

כדי לנסות את המתודה נעבוד עם מערך של מספרים ופונקציה רקורסיבית sorted_arr_to_bst() (אותה נשים מחוץ לקלאס) שתעבור באופן שיטתי על איברי המערך ותוסיף באמצעות המתודה insert() לעץ החיפוש הבינארי:

def sorted_arr_to_bst(elements):
    # The idea is to set the middle of the array as the root
    # then recursively do the same thing for the left and right arrays
    if not elements:
        return None

    # Select the middle element
    mid = len(elements) // 2

    # Make the middle element the root of the subtree
    root = BST(elements[mid])
    
    # Left subtree has the values less than arr[mid]
    root.left = sorted_arr_to_bst(elements[:mid])

    # Right subtree has the values greater than arr[mid]
    root.right = sorted_arr_to_bst(elements[mid+1:])
    
    return root

נסביר:

• הפונקציה מקבלת את הפרמטר elements המכיל מערך מידע.
• אם המערך ריק, הפונקציה גמרה, ומחזירה None. זה מקרה הבסיס של הפונקציה הרקורסיבית.
• במקרה הרקורסיבי הפונקציה בוחרת את הפריט האמצעי של המערך והופכת אותו לשורש של עץ החיפוש הבינארי.
• הפונקציה קוראת לעצמה באופן רקורסיבי עבור תת המערכים משמאל ומימין לפריט האמצעי.
• לבסוף, מוחזר צומת השורש של עץ החיפוש אותו בנתה המתודה.

הפונקציה פועלת על ידי חלוקת מערך הקלט לתת-מערכים קטנים יותר ובניית עץ החיפוש הבינארי על ידי קריאות רקורסיביות חוזרות ונשנות לעצמה. בכל קריאה מוגדר האלמנט האמצעי של כל תת-מערך בתור צומת השורש של תת העץ. התהליך נמשך עד לביקור בכל תתי-המערכים. התוצאה הסופית היא עץ חיפוש בינארי מאוזן. כאשר עץ בינארי מאוזן Balanced Binary Search Tree הוא מבנה נתונים בו גובהם של שני תת-העצים השמאלי והימני של כל צומת אינו שונה ביותר מ-1.

ננסה את הפונקציה על מערך מספרים:

if __name__ == "__main__":
    numbers = [6, 1, -1, -8, 5, 2, 28, 17, 12, 33]
    # The array must first  be sorted
    numbers.sort()
    
    # Call the function to build a tree
    numbers_tree = sorted_arr_to_bst(numbers)

תיכף נראה דרכים לראות שהמידע מסודר כמצופה. בינתיים אציג המחשה שיצרתי באמצעות קוד פייתון שמצאתי ב-https://stackoverflow.com

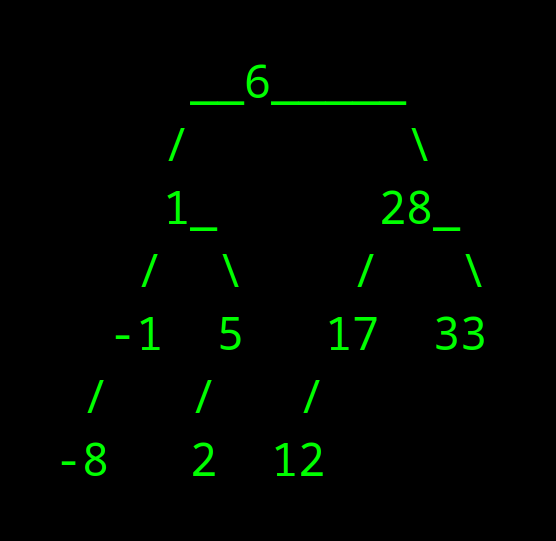
להלן הקוד להצגה של העץ:

def display(self):
    lines, *_ = self._display_aux()
    for line in lines:
        print(line)
def _display_aux(self):
    """Returns list of strings, width, height, and horizontal coordinate of the root."""
    # No child.
    if self.right is None and self.left is None:
        line = '%s' % self.data
        width = len(line)
        height = 1
        middle = width // 2
        return [line], width, height, middle

    # Only left child.
    if self.right is None:
        lines, n, p, x = self.left._display_aux()
        s = '%s' % self.data
        u = len(s)
        first_line = (x + 1) * ' ' + (n - x - 1) * '_' + s
        second_line = x * ' ' + '/' + (n - x - 1 + u) * ' '
        shifted_lines = [line + u * ' ' for line in lines]
        return [first_line, second_line] + shifted_lines, n + u, p + 2, n + u // 2

    # Only right child.
    if self.left is None:
        lines, n, p, x = self.right._display_aux()
        s = '%s' % self.data
        u = len(s)
        first_line = s + x * '_' + (n - x) * ' '
        second_line = (u + x) * ' ' + '' + (n - x - 1) * ' '
        shifted_lines = [u * ' ' + line for line in lines]
        return [first_line, second_line] + shifted_lines, n + u, p + 2, u // 2

    # Two children.
    left, n, p, x = self.left._display_aux()
    right, m, q, y = self.right._display_aux()
    s = '%s' % self.data
    u = len(s)
    first_line = (x + 1) * ' ' + (n - x - 1) * '_' + s + y * '_' + (m - y) * ' '
    second_line = x * ' ' + '/' + (n - x - 1 + u + y) * ' ' + '' + (m - y - 1) * ' '
    if p < q:
        left += [n * ' '] * (q - p)
    elif q < p:
        right += [m * ' '] * (p - q)
    zipped_lines = zip(left, right)
    lines = [first_line, second_line] + [a + u * ' ' + b for a, b in zipped_lines]
    return lines, n + m + u, max(p, q) + 2, n + u // 2

סריקת העץ

סריקת עץ tree traversal (=מעבר) היא תהליך שבו מבקרים בצמתים של העץ באופן שיטתי, פעם אחת בכל צומת. נשתמש בתהליך סריקת העץ לצורך ניתוח וכדי לעשות מניפולציות של עצים.

קיימות שתי אסטרטגיות לסריקת עצים: BFS (Breadth-First Search) ו-DFS (Depth-First Search). במדריך זה נתרכז ב-DFS.

Depth-First Search (DFS) - הוא אלגוריתם לסריקת גרפים (בהם גם עצים) שסורק הכי רחוק שהוא יכול לאורך כל ענף של עץ לפני שהוא פונה לאחור להשלים את מלאכת הסריקה של ענפים שהוא עוד לא ביקר בהם.

נשתמש באסטרטגיה DFS לסריקת עצים כשאנחנו מעוניינים לחפש צומת או נתיב מסוימים, לבדוק קישוריות בין צמתים או לצורך חקירת/תיאור מבנה העץ.

ניתן ליישם DFS באמצעות שלוש אסטרטגיות שונות: pre-order ,in-order ו post-order.

סריקה pre-order מבקרת קודם כל בצומת הנוכחי, אח"כ בתת-העץ השמאלי, ולבסוף בתת-העץ הימני.

סריקה in-order מבקרת קודם כל בתת-העץ השמאלי, לאחר מכן בצומת הנוכחי, ולבסוף בתת-העץ הימני.

סריקה post-order מבקרת קודם כל בתת-העץ השמאלי, לאחר מכן בתת-העץ הימני, ולבסוף בצומת הנוכחי.

איך להבין את שם הסריקה? סריקת תת העץ השמאלי מקדימה תמידה את סריקת תת העץ הימני. לפני order מציינים את מיקום הצומת הנוכחי בסדר המעבר. אם pre (=לפני) אז הצומת הנוכחי בא לפני. אם in (=בתוך) אז הצומת הנוכחי בא באמצע בין תתי העצים השמאלי והימני. אם post (=אחרי) אז הצומת הנוכחי בא אחרי תתי העצים השמאלי והימני.

נוסיף לקלאס מתודה in_order_traversal לביצוע סריקה in_order של עץ בינארי מה שאומר ביקור על פי סדר קודם כל בתת העץ השמאלי, אח"כ בצומת הנוכחי ולבסוף בתת העץ הימני:

def in_order_traversal(self):
    elements = []

    if self is None:
        # Return an empty list if the tree is empty
        return elements

    
    # 1. Visit the left subtree
    if self.left:
        elements += self.left.in_order_traversal()
      
    # 2. Visit the base node
    elements.append(self.data)
    
    # 3. Visit the right subtree
    if self.right:
        elements += self.right.in_order_traversal()
    
    return elements

ננסה את המתודה in_order_traversal():

if __name__ == "__main__": 
    numbers = [6, 1, -1, -8, 5, 2, 28, 17, 12, 33] 
    # The array must first be sorted
    numbers.sort() 
    # Call the function to build a tree
    numbers_tree = sorted_arr_to_bst(numbers)
    print(numbers_tree.in_order_traversal())

התוצאה:

[-8, -1, 1, 2, 5, 6, 12, 17, 28, 33]

נסביר את המתודה in_order_traversal():

• המתודה יוצרת מערך elements לאחסון הצמתים לפי סדר.
• 1. היא מבקרת באופן רקורסיבי בתת העץ השמאלי על ידי קריאה ל-in_order_traversal()  על הילד השמאלי, אם הוא קיים. האלמנטים המוחזרים מצורפים לרשימת האלמנטים.
  2. היא מבקרת בצומת הנוכחי ומוסיפה את ה-data שלו (self.data) לרשימת האלמנטים.
  3. היא מבקרת באופן רקורסיבי בתת העץ הימיני על ידי קריאה ל-in_order_traversal()  על הילד הימיני, אם הוא קיים. האלמנטים המוחזרים מצורפים לרשימת האלמנטים.
• לבסוף, היא מחזירה את האלמנטים ממוינים לפי סדר עולה.

סיבוכיות הזמן time complexity של המתודה in_order_traversal() היא O(n), כאשר n הוא מספר הצמתים בעץ החיפוש הבינארי בגלל שהמתודה מבקרת בכל צומת פעם אחת בדיוק על מנת לבצע את הסריקה לפי הסדר.

סיבוכיות המרחב space complexity של המתודה in_order_traversal() היא O(h), כאשר h הוא גובה עץ החיפוש הבינארי. הסיבה לכך היא שהמתודה משתמשת בקריאות רקורסיביות לסריקת העץ, והעומק המרבי של הרקורסיה נקבע לפי גובה העץ. במקרה הגרוע ביותר, כאשר העץ מוטה וגובהו n (בדומה לרשימה מקושרת), מרחב הזיכרון הנדרש ל-stack הרקורסיה הוא O(n) (הרעיון הוא של ערימה stack כאשר כל קריאה רקורסיבית לפונקציה מוסיפה עוד קומה לערימה קרא על זיכרון ערימה stack memory וזיכרון מחסנית). עם זאת, בעץ חיפוש בינארי מאוזן, הגובה הוא לוגריתמי (בסיס 2 כי העץ מתפצל בכל רמה ל-2) וכתוצאה מכך מרחב הזיכרון תלוי ב-n מספר הפריטים ועומד על O(log n).

באופן דומה, המתודה pre_order_traversal() מבצעת סריקה לפי סדר. קודם כל, צומת נוכחי, אח"כ תת עץ שמאלי ולבסוף תת עץ ימני:

def pre_order_traversal(self):
    elements = []

   if self is None:
       # Return an empty list if the tree is empty
       return elements
    
    # 1. Visit the base node
    elements.append(self.data)
    
    # 2. Visit the left subtree
    if self.left:
        elements += self.left.pre_order_traversal()
    
    # 3. Visit the right subtree
    if self.right:
        elements += self.right.pre_order_traversal()
    
    return elements

נבחן את המתודה pre_order_traversal():

if __name__ == "__main__":
    numbers = [6, 1, -1, -8, 5, 2, 28, 17, 12, 33] 
    # The array must first be sorted
    numbers.sort() 
    # Call the function to build a tree
    numbers_tree = sorted_arr_to_bst(numbers)
    print(numbers_tree.pre_order_traversal())

התוצאה:

[6, 1, -1, -8, 5, 2, 28, 17, 12, 33]

נחזור ונציץ בעץ כדי להבין את התוצאה:

1. קודם כל מבקרים בצומת השורש (6).
2. אח"כ מבקרים בתת העץ השמאלי וממנו סורקים לתת העץ השמאלי שלו וכיו"ב, ולכן (1 -〉 -1 -〉 -8).
3. אח"כ חוזרים עד לשורש תת העץ השמאלי (1) וממנה סורקים את תת העץ הימני ואח"כ את תת העץ הימני שלו וכיו"ב, ולכן (5 -〉 2).
4. חוזרים עד לשורש העץ ומשם סורקים את תת העץ הימני (28).
5. בתוך תת העץ הימני ראשית סורקים את תת העץ השמאלי (17 -〉 12).
6. עדיין בתוך תת העץ הימני חוזרים לשורש תת העץ הימני (28), וממנו עוברים לסרוק את תת העץ הימני (33).

באופן דומה, המתודה post_order_traversal() מבצעת סריקה לפי סדר. קודם כל, תת עץ שמאלי, אח"כ ימני, ובסוף צומת נוכחי:

def post_order_traversal(self):
    elements = []

   if self is None:
       # Return an empty list if the tree is empty
       return elements
    
    # 1. Visit the left subtree
    if self.left:
        elements += self.left.post_order_traversal()
    
    # 2. Visit the right subtree
    if self.right:
        elements += self.right.post_order_traversal()

    # 3. Visit the base node
    elements.append(self.data)
    
    return elements

חיפוש בעץ בינארי

פעולת החיפוש בעץ בינארי היא אחת הסיבות העיקריות לשימוש במבנה נתונים זה.

נוסיף לקלאס מתודה לחיפוש בתוך עץ בינארי search():

def search(self, val):
    # Check if the current node's value matches the target value
    if self.data == val:
        return self
        
    # If the target value is less than the current node's value,
    # navigate to the left subtree (if it exists) and recursively search
    if self.data > val and self.left:
        return self.left.search(val)

    # If the target value is greater than the current node's value,
    # navigate to the right subtree (if it exists) and recursively search
    if self.data < val and self.right:
        return self.right.search(val)
    
    # If the target value is not found and there are no more subtrees to search,
    # return None to indicate that the value does not exist in the tree
    return None

נבחן את מתודת החיפוש search():

if __name__ == "__main__":
    numbers = [6, 1, -1, -8, 5, 2, 28, 17, 12, 33]
    
    # Sort the numbers array in ascending order
    numbers.sort()

    # Build a binary search tree from the sorted array
    numbers_tree = sorted_arr_to_bst(numbers)

    # Perform some tests using the search function

    # Test Case 1: Search for an existing value
    value = 5
    res = numbers_tree.search(value)
    if res:
        print(f"{res.data} exists in the tree")
    else:
        print(f"{value} does not exist in the tree")
    
    # Test Case 2: Search for the minimum value
    value = -8
    res = numbers_tree.search(value)
    if res:
        print(f"{res.data} exists in the tree")
    else:
        print(f"{value} does not exist in the tree")
    
    # Test Case 3: Search for the maximum value
    value = 33
    res = numbers_tree.search(value)
    if res:
        print(f"{res.data} exists in the tree")
    else:
        print(f"{value} does not exist in the tree")
    
    # Test Case 4: Search for a non-existing value
    value = 10
    res = numbers_tree.search(value)
    if res:
        print(f"{res.data} exists in the tree")
    else:
        print(f"{value} does not exist in the tree")
    
    # Test Case 5: Search for a non-existing value
    value = -12
    res = numbers_tree.search(value)
    if res:
        print(f"{res.data} exists in the tree")
    else:
        print(f"{value} does not exist in the tree")
    
    # Test Case 6: Search for a non-existing value
    value = 80
    res = numbers_tree.search(value)
    if res:
        print(f"{res.data} exists in the tree")
    else:
        print(f"{value} does not exist in the tree")

התוצאה:

5 exists in the tree
-8 exists in the tree
33 exists in the tree
10 does not exist in the tree
-12 does not exist in the tree
80 does not exist in the tree

נסביר את המתודה search():

• המתודה מתחילה מהשוואת הערך המבוקש (val) לערך הצומת הנוכחי (self.data). אם הם שווים, זה אומר שהערך נמצא בצומת הנוכחי, והמתודה מחזירה self.
• אם הערך המבוקש קטן יותר מערך הצומת הנוכחי (self.data) ויש תת-עץ שמאלי (self.left), המתודה קוראת לעצמה רקורסיבית על תת-העץ השמאלי כדי להמשיך את החיפוש.
• אם הערך המבוקש גדול יותר מערך הצומת הנוכחי (self.data) ויש תת-עץ ימני (self.right), המתודה קוראת לעצמה רקורסיבית על תת-העץ הימני לצורך המשך החיפוש.
• אם הערך המבוקש לא נמצא ואין יותר תת-עצים לחפש המתודה מחזירה None.

המתודה מבצעת חיפוש (DFS) בעץ החיפוש הבינארי, תוך שימוש ב רקורסיה כדי לסרוק את תתי העצים. היא משתמשת בתכונת עץ החיפוש הבינארי כדי לצמצם במהירות את מרחב החיפוש.

תהליך החיפוש בעץ חיפוש בינארי יעיל הודות למבנה העץ. בכל שלב של החיפוש, מרחב החיפוש פוחת בערך בחצי. כלומר, עבור כל השוואה שנעשתה, החיפוש ממשיך לעץ השמאלי או הימני, ומבטל חלק משמעותי ממרחב החיפוש שנותר. כתוצאה מכך, לפעולת החיפוש בעץ חיפוש בינארי זמן ריצה לוגריתמי O(log N) במקרים הממוצעים או הטובים ביותר, כאשר N הוא מספר הצמתים בעץ.

לשם השוואה, חיפוש במערך בדרך כלל כרוך בבדיקה רציפה של כל אלמנט עד שמוצאים התאמה או שמגיעים לסוף הרצף מה שאומר שזמן הריצה הגרוע ביותר הוא לינארי O(N). הבדל זה בזמני הריצה בין מערכים לעצי חיפוש בינאריים הופך משמעותי יותר ככל שהרצף מתארך. לדוגמה, אם מרחב החיפוש יכלול 1000 פריטי מידע, משך הריצה הארוך ביותר של מערך יהיה 1000 לעומתו עץ בינארי יעשה את העבודה ב-10 מעברים לכל היותר.

מציאת הצומת המינימלי בעץ חיפוש בינארי

בשביל למצוא את הצומת בעל הערך המינימלי בעץ חיפוש בינארי נשתמש ברקורסיה אשר סוגרת בכל פעם על תת העץ השמאלי המכיל את האלמנטים הקטנים יותר מאשר הצומת הנוכחי עד שמגיעים לצומת ללא ילד שמאלי שהוא זה שיכיל את הערך הנמוך ביותר. המתודה find_min() מחזירה את הצומת בעל הערך הנמוך ביותר:

def find_min(self):
        if not self.left:
            return self
        return self.left.find_min()

• מקרה הבסיס: במידה והצומת הנוכחי לא מכיל ילד שמאלי `if not self.left`, משמעות הדבר שהצומת הנוכחי הוא הקטן ביותר בעץ. לפיכך, המתודה מחזירה את הצומת `return self`
• מקרה רקורסיבי: אם לצומת הנוכחי קיים ילד שמאלי, המתודה קוראת באופן רקורסיבי לעצמה עבור הילד השמאלי `return self.left.find_min()`

נבחן את המתודה:

if __name__ == "__main__":
    numbers = [6, 1, -1, -8, 5, 2, 28, 17, 12, 33]
    numbers.sort()
    numbers_tree = sorted_arr_to_bst(numbers)
    res = numbers_tree.find_min()
    print(f"The minimum value is {res.data}")

• התוצאה -8 היא בהתאם לצפי.

מחיקת תת עץ מתוך עץ בינארי

כאשר מוחקים צומת מעץ חיפוש בינארי, ישנם שלושה תרחישים עיקריים שיש לקחת בחשבון:

1. מחיקת צומת עלה: אם הצומת שצריך למחוק הוא עלה (כלומר, אין לו ילדים), המחיקה פשוטה. הצומת יכול פשוט להימחק מהעץ, וההפניה של הצומת האב אליו יכולה להיות מעודכנת ל-None.

2. מחיקת צומת עם ילד יחיד: אם הצומת שצריך למחוק יש לו רק ילד אחד, הילד יכול לתפוס את מקומו של הצומת שנמחק בעץ. ההפניה של הצומת האב אל הצומת שנמחק מתעדכנת כדי להצביע על נכדו.

3. מחיקת צומת עם שני ילדים: כאשר הצומת שצריך למחוק יש לו שני ילדים, התהליך קצת יותר מורכב. הרעיון המרכזי הוא למצוא את הערך המקסימלי בתת-העץ השמאלי של הצומת או את הערך המינימלי בתת-העץ הימני של הצומת. הצומת הזה ישמש להחלפת הצומת שנמחק. עושים את זה כדי לשמור על תכונות עץ החיפוש הבינארי, מכיוון שהערך ההחלפה גדול יותר מכל הערכים בתת-העץ השמאלי או קטן יותר מכל הערכים בתת-העץ הימני.

לאחר המחיקה, עץ החיפוש הבינארי צריך לשמור על שלמות מבנית ולקיים את תכונות עץ החיפוש הבינארי, כאשר תת-העץ השמאלי מכיל ערכים קטנים יותר מצומת השורש, ותת-העץ הימני מכיל ערכים גדולים יותר מהשורש.

חשוב לציין כי בכל תרחישי המחיקה, יש להקפיד לעדכן את ההפניות והחיבורים בתוך העץ כדי להבטיח את נכונותו ושלמותו.

המתודה delete() להלן תשמש למחיקה של צמתים מתוך העץ:

def delete(self, val):
    if val < self.data:
        if self.left:
            self.left = self.left.delete(val)
    elif val > self.data:
        if self.right:
            self.right = self.right.delete(val)
    else:
        if self.left is None and self.right is None:
            # Case 1: Node to delete is a leaf node
            return None
        elif self.left is None:
            # Case 2: Node to delete has only a right child
            return self.right
        elif self.right is None:
            # Case 3: Node to delete has only a left child
            return self.left
        else:
            # Case 4: Node to delete has both left and right children
            successor = self.right.find_min()
            self.data = successor.data
            self.right = self.right.delete(successor.data)

    return self

נבחן את המתודה המשמשת למחיקה:

if __name__ == "__main__":
    numbers = [6, 1, -1, -8, 5, 2, 28, 17, 12, 33]
    
    # Sort the numbers array in ascending order
    numbers.sort()

    # Build a binary search tree from the sorted array
    numbers_tree = sorted_arr_to_bst(numbers)
    
    # Display tree prior to deletion
    print("Tree before deletion:")
    numbers_tree.display()
    print()
    
    # Remove leaf node (Case 1)
    numbers_tree.delete(33)
    
    print("Tree after deleting leaf node:")
    numbers_tree.display()
    print()
    
    # Remove parent of a single child (Case 2)
    numbers_tree.delete(17)
    
    print("Tree after deleting parent of a single child:")
    numbers_tree.display()
    print()
    
    # Remove parent of two children (Case 3)
    numbers_tree.delete(1)
    
    print("Tree after deleting parent of two children:")
    numbers_tree.display()
    print()
    
    # Remove root node (Case 4)
    numbers_tree.delete(6)
    
    print("Tree after deleting root node:")
    numbers_tree.display()
    print()
    
    # Remove non-existing node
    numbers_tree.delete(888)
    
    print("Tree after deleting non-existing node:")
    numbers_tree.display()
    print()

לסיכום

עץ בינארי ועץ חיפוש בינארי (BST) הם מבני נתונים בסיסיים בעולם המחשבים שיש להם מגוון יישומים. עץ בינארי מורכב מצמתים המחוברים באמצעות יחסי הורה-ילד, בעוד ש-BST הוא סוג מסוים של עץ בינארי שיש לו את תכונת עץ החיפוש הבינארי לפיה מסודרים הצמתים שלו.

פעולת החיפוש ב-BST מנצלת את תכונת עץ החיפוש הבינארי כדי למצוא ערך מסוים ביעילות. עם כל השוואה, מרחב החיפוש מצטמצם פי שניים, ועל כן סיבוכיות הזמן של הפעולה היא לוגריתמית O(log N) בממוצע, כאשר N הוא מספר הצמתים. פעולת החיפוש ב-BST היא מהירה משמעותית יותר ממערכים בהם החיפוש דורש זמן ליניארי (O(N)).

מבחינת יעילות, עצי חיפוש בינארי מציעים פעולות חיפוש, הכנסה ומחיקה מהירות יותר לעומת מערכים, במיוחד עבור מערכי נתונים גדולים. סיבוכיות הזמן הלוגריתמית שלהם (O(log N)) מאפשרת טיפול יעיל בנתונים מסודרים וערכים דינמיים.

לעצי חיפוש בינארי ישנם יישומים שונים. שלושה יישומים עיקריים כוללים:

1. חיפוש ושחזור: עצי BST מצטיינים בחיפוש ערכים ספציפיים בתוך מערכי נתונים מסודרים. תכונות החיפוש הבינארי מאפשרות סריקה יעילה, מה שהופך אותם מתאימים למשימות כמו יישומי מילון או אינדוקס מסדי נתונים.

2. מיון: עצי BST יכולים לשמש למיון סדרה של ערכים על ידי הכנסתם לעץ וביצוע סריקה בינארית מה שנותן רשימה ממוינת של פריטים. עם זאת, חשוב לציין שאלגוריתמי מיון מיוחדים כמו quicksort או mergesort הם בדרך כלל יעילים יותר למיון כללי.

3. שאילתות טווח: מבנה BST מאפשר שאילתות טווח, שבהן אנו יכולים לאחזר ביעילות את כל הפריטים בטווח נתון. על ידי ניצול אלגוריתם החיפוש הבינארי, אנו יכולים לנווט בעץ כדי למצוא את הערכים הקטנים והגדולים ביותר בטווח הנתון.

לסיכום, עצים בינאריים ועצי חיפוש בינאריים הם מבני נתונים עוצמתיים הודות ליעילות פעולות החיפוש, הכנסה ומחיקה. סיבוכיות הזמן הלוגריתמית והתכונות הספציפיות שלהם הופכים אותם לשימושים במגוון תרחישים, והם מציעים יעילות משופרת לעומת מערכים עבור משימות כמו חיפוש, מיון ושאילתות טווח.

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

חידה תכנותית : סריקת עץ בינארי על פי סדר הרמות

חידה תכנותית : מציאת האב המשותף הרחוק ביותר LCA בעץ בינארי

General Tree data structure עץ נתונים

יישום תורת הגרפים בפייתון - חלק א

Linked list - רשימה מקושרת - תיאוריה, קוד ואתגרים תכנותיים

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים