אלגוריתם Selection Sort מיון בחירה

אלגוריתם "מיון בחירה" Selection sort הוא כמעט האלגוריתם הקל ביותר לכתיבה ולהסבר המשמש לסידור פריטים בסדר עולה או יורד.

עיקרון הפעולה של האלגוריתם Selection sort הוא פשוט. מחלקים את מערך הפריטים שאותו צריך לסדר לשניים: בצד אחד הפריטים המסודרים, ובצד השני הפריטים שעוד צריך לסדר. בשביל הסידור נעזרים בלולאה. בכל פעם שהלולאה רצה היא מוצאת את הפריט הקטן ביותר, ומעבירה אותו מהרשימה הלא מסודרת לסוף הרשימה המסודרת.

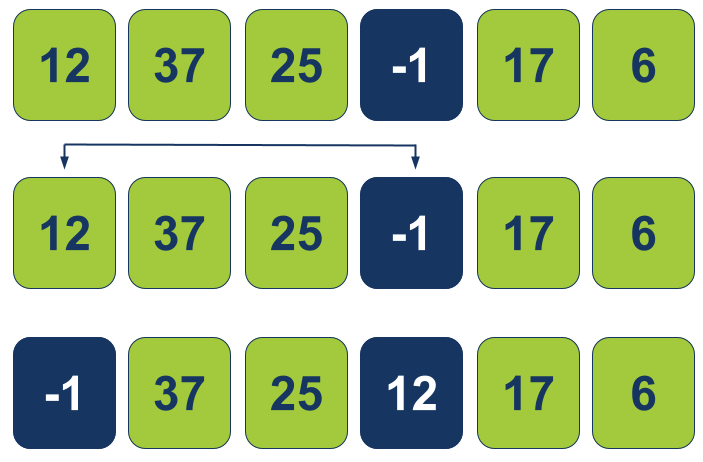
נתחיל מהצבת הסמן על העמדה הראשונה (אינדקס 0):

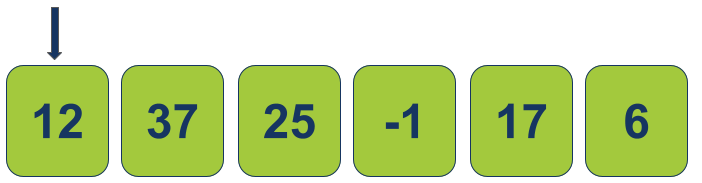
המטרה היא למצוא את הערך הקטן ביותר במערך ולהחליף אותו עם הערך הנמצא מתחת לסמן:

• איתרנו וסימנו את הערך הקטן ביותר במערך שהוא -1.
• ואז החלפנו את מיקום הערך -1 עם הערך עליו מצביע הסמן באינדקס 0.

נקדם את הסמן במקום אחד. מאינדקס 0 לאינדקס 1:

נמצא את הערך הקטן ביותר במערך ונחליף אותו עם הערך הנמצא מתחת לסמן בעמדה מספר 1:

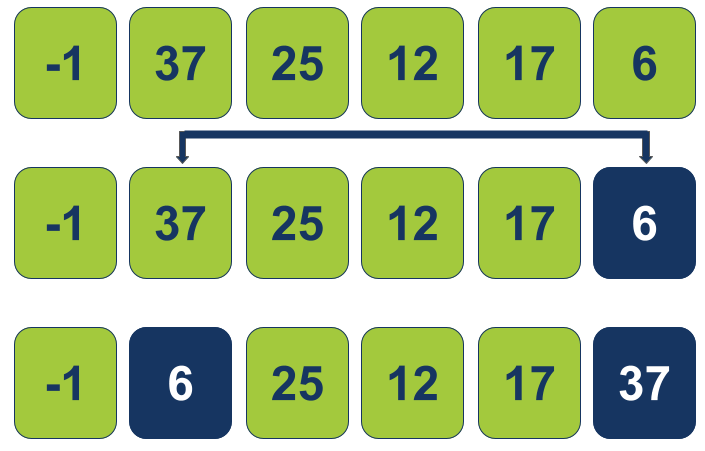
• איתרנו וסימנו את הערך הקטן ביותר במערך שהוא 6.
• ואז החלפנו מקומות בין הערך 6 לבין הערך שנמצא מתחת לסמן באינדקס 1.

נמשיך להתקדם. נעביר את הסמן מהאינדקס שמספרו 1 לאינדקס שמספרו 2:

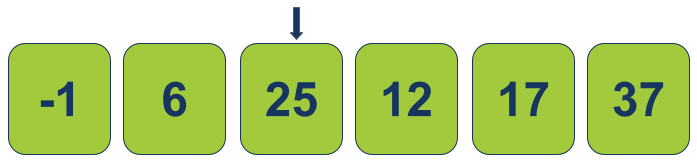
אפשר לראות שיצרנו בתוך אותו המערך שני אגפים:

• אגף שמאלי מסודר
• אגף ימני שאינו מסודר

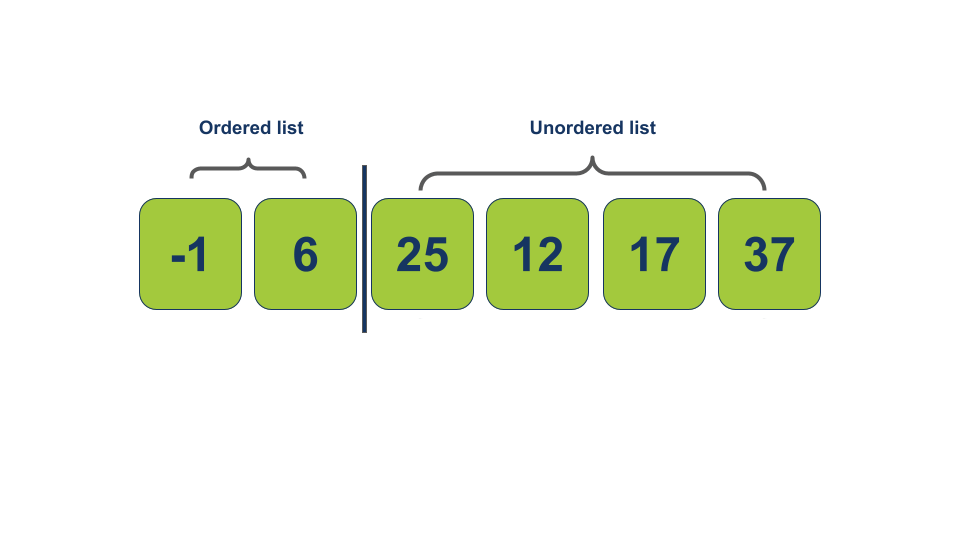
התפקיד של האלגוריתם הוא להעביר את הערכים לפי סדר מהאגף הלא מסודר של המערך לאגף המסודר. אחד אחד עד שהלולאה מסיימת לרוץ מועברים כל הערכים לצד המסודר ואז המערך כולו הופך למסודר.

יישום אלגוריתם Selection sort באמצעות קוד פייתון

נתחיל את ההסבר מהבנת הקוד הפשוט הבא אשר משתמש בלולאה למציאת הערך הנמוך ביותר ברשימה:

def find_smallest(arr):
    # by default the first element of the array
    # has the smallest value
    idx = 0
    smallest_val_idx = 0
    smallest_val = arr[0]
    for i in range(idx, len(arr)):
           if arr[i] < smallest_val:
               # once it finds a smaller value
               # it sets it as the new min
               smallest_val_idx = i
               smallest_val = arr[i]
    # return the index of the smallest value
    return smallest_val

• הפונקציה מקבלת מערך
• הלולאה מתחילה לרוץ משמאל (אינדקס 0 של המערך), ורצה עד לסוף המערך. 
• מאתחלים את התהליך בזה שמניחים שהערך הנמוך ביותר נמצא באינדקס 0.
• במידה והלולאה מוצאת ערך נמוך יותר מ-smallest_val היא מציבה מחדש את הערכים smallest_val_idx ו- smallest_val.
• הפונקציה מחזירה את האינדקס של הערך הנמוך ביותר.

נבדוק שהקוד עובד:

print(find_smallest([1, -3, -8, 9, 10, -2])) # -8

אמרנו שיש לנו 2 רשימות: רשימה מסודרת משמאל, ולא מסודרת מימין. אנחנו מתחילים להריץ את האלגוריתם כאשר הרשימה המסודרת לא מכילה פריטים.

בכל פעם שהאלגוריתם רץ הוא צריך להעביר את הפריט הקטן ביותר לסוף הרשימה המסודרת, למיקום במערך הנמצא מתחת לסמן. האלגוריתם עובד in place מה שאומר שעושים כל הפעולות בתוך המערך המקורי. בהתאם, כדי להעביר פריט ממקומו צריך להחליף swap את המקום שלו עם פריט אחר. האלגוריתם צריך להחליף את המיקום של האלמנט בעל הערך הנמוך ביותר עם הפריט שנמצא מתחת לסמן. בפעם הראשונה בה האלגוריתם רץ, הוא צריך להחליף מקומות בין הערך הנמוך ביותר במערך לבין האלמנט הנמצא מתחת לסמן באינדקס 0.

נוסיף קוד המשמש להחלפה בין האלמנטים שירוץ אחרי שהלולאה סיימה לרוץ:

def put_smallest_val_at_index_0(arr):
    idx = 0
    smallest_val_idx = 0
    smallest_val = arr[0]
    for i in range(idx, len(arr)):
        if arr[i] < smallest_val:
            smallest_val_idx = i
            smallest_val = arr[i]

    if smallest_val_idx != idx:
        # swap
        arr[smallest_val_idx], arr[idx] = arr[idx], arr[smallest_val_idx]
        
    return arr

• אחרי שהלולאה מסיימת לרוץ ומוצאת את פריט הרשימה בעל הערך הנמוך ביותר מתבצעת החלפה בין האלמנטים.
• ההחלפה בין אלמנטים במערך בפייתון נעשית באמצעות שורה אחת בלבד.
• התנאי להחלפה הוא שהאינדקס של הערך הנמוך ביותר שונה מהאינדקס הנוכחי מעליו עומד הסמן (אינדקס 0 בשלב זה).

יפה מאוד! עד עכשיו ראינו איך להחליף את מיקום הפריט הראשון של הרשימה עם הפריט הקטן ברשימה. אבל מה לגבי הפריט השני ברשימה, השלישי, הרביעי, וכיו"ב?

בשביל שהפטנט עם הלולאה שמוצאת את האלמנט הקטן ביותר ומחליפה מיקומים תעבוד עבור כל הרשימה ולא רק עבור הפריט הראשון נוסיף לולאה נוספת חיצונית שרצה מתחילת המערך ועד סופו, ובכל פעם מקדמת את האינדקס במקום אחד:

def selection_sort(arr):
    # outer loop to advance the index
    # 1 position at a time
    for idx in range(0, len(arr)):
        smallest_val_idx = idx
        smallest_val = arr[idx]
        
        # inner loop to find the smallest
        # value element in the unordered     
        # part of the array
        for i in range(idx+1, len(arr)):
            if arr[i] < smallest_val:
                smallest_val_idx = i
                smallest_val = arr[i]

        # swap
        if smallest_val_idx != idx:
            arr[smallest_val_idx], arr[idx] = arr[idx], arr[smallest_val_idx]
            
    # return the sorted array
    return arr

• הלולאה החיצונית רצה על המערך מתחילתו ועד סופו, ומקדמת את האינדקס הרלוונטי בכל פעם ב-1, האינדקס הוא העמדה האחרונה של הרשימה המסודרת, שהולכת ומתארכת בכל איטרציה בפריט 1
• הלולאה הפנימית רצה על החלק הלא מסודר של המערך, ומחפשת ערך קטן יותר מזה הנמצא תחת הסמן. אחרי שהלולאה הפנימית מסיימת לרוץ מתבצעת החלפה של מיקום האלמנט הקטן ביותר ברשימה עם מיקום האלמנט אשר מתחת לסמן.

נשפר את הקוד בשני אופנים:

1. כל פעם שהלולאה רצה אנחנו מחשבים מחדש את אורך המערך. זה בזבוז של משאבי מחשוב אז נחשב את אורך המערך פעם אחת בלבד ונשתמש בזה בכל מקום אח"כ.
2. בגלל הדינמיקה של ההחלפות אין צורך שהלולאה החיצונית תרוץ עד הפריט האחרון של המערך כי ההנחה היא שכשהלולאה מגיעה לעמדה האחרונה כבר בוצעו ההחלפות המציבות בעמדה האחרונה של המערך את הערך הגבוה ביותר אז ניתן ללולאה לרוץ רק עד הפריט האחד לפני אחרון של המערך.

def selection_sort(arr):
    # cache the size of the array
    size = len(arr)
    
    # outer loop to advance the index
    # 1 position at a time
    for idx in range(0, size-1):
        smallest_val_idx = idx
        smallest_val = arr[idx]
        
        # inner loop to find the smallest
        # value element in the unordered     
        # part of the array
        for i in range(idx+1, size):
            if arr[i] < smallest_val:
                smallest_val_idx = i
                smallest_val = arr[i]
        # swap
        if smallest_val_idx != idx:
            arr[smallest_val_idx], arr[idx] = arr[idx], arr[smallest_val_idx]
            
    # return the sorted array
    return arr

נבחן את הפונקציה selection_sort() אותה כתבנו במדריך:

arrs = [
[],
[-1, 5, 85, 192],
[42, 6, 3, 5, 1, -3],
[5, 65, 72, 16, 13, 28, -1],
[-8, 42, 13, 6, 7],
]

for arr in arrs:
    print(selection_sort(arr))

הערכת ביצועי האלגוריתם

משך הזמן לביצוע של אלגוריתם "מיון בחירה" Selection sort הוא O(n^2) בגלל שמריצים שתי לולאות אחת בתוך השנייה. כל אחת מהלולאות תורמת משך ביצוע של O(n), והמכפלה בין זמני הביצוע של שתי הלולאות נותנת O(n^2).

קומפלקסיות המקום היא O(1) בגלל שאין צורך באחסון נוסף כדי לבצע את האלגוריתם.

הערכת אלגוריתם Selection sort

יתרון מרכזי של אלגוריתם "מיון בחירה" selection sort הוא שקל להבין ולכתוב אותו.

החיסרון המרכזי הוא קופלקסיות זמן O(n^2) מה שהופך אותו לבעייתי ליישום ככל שעובדים עם רשימת נתונים ארוכה יותר. אם נרצה להאיץ משמעותית את משך ביצוע תהליך המיון נעדיף את האלגוריתמים merge sort ו-quick sort שיש להם קומפלקסיות זמן O(n*logn).

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

אלגוריתם חיפוש בינארי - מהבנה ליישום

big-O ביטוי ליעילות הקוד

פונקציות למדא (lambda) אנונימיות של פייתון

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים