stacks, ערימות וחידות

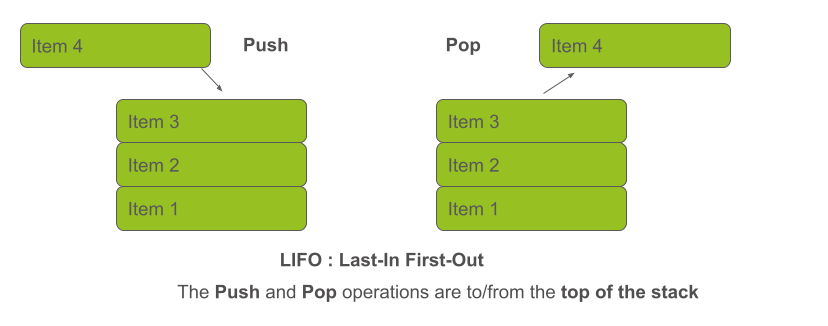
ערימה stack היא מבנה נתונים שעובד לפי העיקרון של אחרון נכנס ראשון יוצא (Last-In-First-Out) LIFO. משמעות הדבר שהפריט האחרון שנוסף לערימה הוא הראשון שיוסר ממנה.

אנחנו יכולים להוסיף פריטים רק לראשה של-stack ערימה, ואם אנחנו רוצים להסיר פריטים אנחנו חייבים גם כן להסיר מראש הערימה. אתה יכול לחשוב על ערימת ספרים המונחת על השולחן: אתה יכול להוסיף ספר לראש הערימה, ואם אתה רוצה להסיר ספר אתה יכול להסיר מראש הערימה.

משתמשים ב-stacks ערימות בשביל פונקציות שאפשר להחזיר אחורנית undo/redo בדפדפן או בעורכי טקסט (דוגמת וורד) "undo stack" כאשר כל שינוי למסמך נוסף לראש הערימה, וניתן לחזור אחורנית על ידי כך שמסירים בכל פעם את השינוי האחרון שנמצא בראש הערימה.

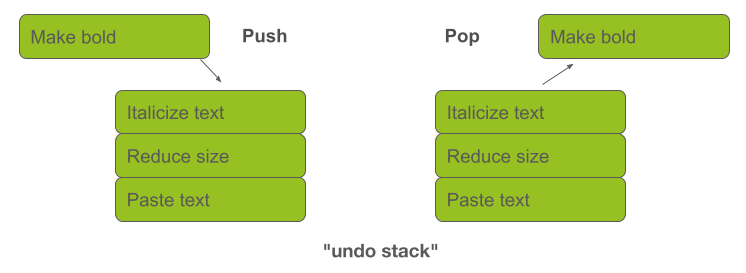
כשאנחנו מיישמים stack בקוד להוספת פריט לראש הערימה אנחנו קוראים push ולהסרת פריט pop.

נראה דוגמה לקוד בשביל יישום ערימה stack פשוטה מבוססת רשימה list של פייתון:

# create an empty list to represent the stack
stack = []  

# push some items onto the stack
stack.append('apple')
stack.append('banana')
stack.append('cherry')

# pop an item off the top of the stack
top_item = stack.pop()

print(top_item)  # output: 'cherry'
print(stack)     # output: ['apple', 'banana']

• יצרנו רשימה ריקה שקראנו לה "stack" והיא מתפקדת בתור הערימה התכנותית stack. בהמשך, הוספנו 3 פריטים לערימה באמצעות המתודה append() (לא באמצעות push? לא. כי אנחנו עובדים עם רשימה ולא עם קוד ייעודי שעושה stack. אבל רגע, תיכף נגיע לזה). לבסוף הסרנו את הפריט אשר בראש הערימה באמצעות המתודה pop() שגם החזירה את הפריט אותו הסרנו. הדפסנו את הפריט שהוסר מראש הערימה כמו גם את חלקה של הערימה שנותר אחרי הסרת הפריט מראש הערימה.

יישום של Stack באמצעות קלאס collections.deque

יישום של stack באמצעות list של פייתון אינו אופטימלי בגלל שרשימות של פייתון הם דינמיות, המקום שהם תופסות בזיכרון המחשב משתנה על פי הצורך, ושינויים אילה צורכים משאבי מחשוב.

כדי לפתור את הבעיה, אפשר להשתמש במבנה נתונים ייעודי של פייתון דוגמת הקלאס collections.deque. קלאס זה מיועד מראש לעבוד בתור stack ערימה מה שמאפשר לו להיות יעיל יותר עבור הוספת והסרת פריטים, בלי צורך להקצות זיכרון בתהליך יקר כמו שפייתון מפעיל בשביל רשימות מתארכות.

להלן דוגמה ליישום הקלאס collections.deque לצורך יישום stack:

from collections import deque

stack = deque()

stack.append('apple')
stack.append('banana')
stack.append('cherry')

# pop an item off the top of the stack
top_item = stack.pop()

print(top_item)  # output: 'cherry'
print(stack)     # output: deque(['apple', 'banana'])

בשביל ליישם Stack אנחנו צריכים מספר מתודות לכן נשתמש בקלאס עוטף wrapper class שנקרא לו Stack בתוכו ניצור את המתודות הדרושות לנו שיהיו מבוססות על הקלאס collections.deque

from collections import deque

class Stack:
    def __init__(self):
        self.items = deque()

    def push(self, item):
        self.items.append(item)

    def pop(self):
        if len(self.items) > 0:
            return self.items.pop()
        else:
            return None

    def peek(self):
        if len(self.items) > 0:
            return self.items[-1]
        else:
            return None

    def is_empty(self):
        return len(self.items) == 0

    def size(self):
        return len(self.items)

    def __str__(self):
        return f"{self.items}"

הקלאס Stack שכתבנו כולל את המתודות:

• push() - מוסיף פריט לראש הערימה
• pop() - מסיר פריט מראש הערימה ומחזיר אותו. אם הערימה ריקה מחזיר None
• peek() - מאפשר להציץ ולראות מה הפריט בראש הערימה בלי להסיר אותו
• size() - מחזיר את מספר הפריטים בערימה
• is_empty() - מחזיר True אם הערימה ריקה. אחרת מחזיר False.
• __str__ - מחזיר ייצוג טקסטואלי של האובייקט.

הקוד הבא בוחן את הקלאס Stack:

my_stack = Stack()
my_stack.push(1)
my_stack.push(42)


print(my_stack) # deque([1, 42])
print(my_stack.peek()) # 42
print(my_stack) # deque([1, 42])
print(my_stack.pop()) # 42
print(my_stack) # deque([1])
print(my_stack.size()) # 1
print(my_stack.is_empty()) # False
print(my_stack.pop()) # 1
print(my_stack.pop()) # None
print(my_stack.is_empty()) # True

כיצד להשתמש ב-Stack להפיכת סדר התווים במחרוזת?

ניתן להפוך את כיוונם של התווים במחרוזת באמצעות פייתון בדרכים פשוטות. השיטה הפשוטה ביותר משתמשת ב-slicing:

s = "Stacks are fun"
print(s[::-1])

• דרך זו היא יעילה ביותר מבחינה תכנותית. אפשר להשתמש גם בפונקציה reversed.

אבל במדריך זה אנחנו לומדים על שימוש ב-stack. אז נשתמש במה שלמדנו כדי להפוך מחרוזת ולקבל את התווים שלה בסדר הפוך. אתה מוזמן לנסות בעצמך. זה לא מסובך כל מה שצריך הוא להבין ש-stack מאפשר להפוך את כיוונם של רצפים כי סדר השליפה הוא הפוך מסדר ההוספה לערימה.

עכשיו תנסה בעצמך לפתח קוד פייתון אשר משתמש בקלאס Stack כדי להפוך מחרוזות. תשתדל לעשות את זה מבלי להציץ בפתרון.

אם אתה רוצה להיעזר בפתרון הרי הוא לפניך. איך הופכים את כיוונה של מחרוזת על ידי שימוש ב-stack?

def reverse_string(s):
  """
  Reverses a string using a stack.

  Args:
    s: The string to reverse.

  Returns:
    The reversed string.
  """

  # Create a stack to store the characters of the string.
  stack = Stack()

  # Iterate over the characters of the string.
  for c in s:
    # Push the character onto the stack.
    stack.push(c)

  # Iterate over the stack, popping off characters and appending them to a new string.
  reversed_string = ""
  while stack.size():
    reversed_string += stack.pop()

  # Return the reversed string.
  return reversed_string

נבחן את הפונקציה:

print(reverse_string("Python")) # prints "nohtyP"
print(reverse_string("P")) # prints "P"
print(reverse_string("")) # prints
print(reverse_string("100")) # prints "001"

נסביר: הפונקציה "reverse_string" קולטת מחרוזת אותה היא צריכה להחזיר בסדר הפוך. היא משתמשת ב-stacks לאחסון תווי המחרוזת. בשלב ראשון, הפונקציה עוברת על כל תווי המחרוזת על פי הסדר המקורי שלהם, ודוחפת אותם אל תוך הערימה stack. בשלב שני, הערימה מתרוקנת לפי סדר, מראש הערימה ועד לבסיסה. כל פריט שהיא מחזירה הוא תו שמתווסף למחרוזת reversed_string אותה הפונקציה מחזירה.

כיצד להשתמש ב-Stack לזיהוי פלינדרומים?

פלינדרום הוא כל רצף - מילה, ביטוי, מספר - שניתן לקרוא אותו מההתחלה לסוף ומהסוף להתחלה ובכל זאת לקבל את אותו דבר. דוגמאות לפלינדרומים בעברית הם: "שמש", "לבלב", "מוּם תַּחַת מוּם", "ילד נתן דלי". באנגלית: "madam", "kayak", "racecar", "civic" או המשפט: "A man, a plan, a canal: Panama". אפשר גם בספרות: 7777 או תאריכים 11/11/11, 2/2/22

אנחנו יכולים להשתמש ב-Stack כדי לזהות האם מחרוזת היא פלינדרום.

זה השלב שבו אני ממליץ לעצור ולנסות לכתוב פונקציה שמזהה פלינדרומים. לחשוב למה אפשר לזהות פלינדרומים על ידי שימוש ב- stack, ולהשתמש בקלאס Stack כדי לפתור את הבעיה. אחרי שאתם מסיים לכתוב את הפתרון תנסה אותו על מחרוזות שונות כאילו שהם פלינדרומים וכאלו שאינם ותראה שאתה מקבל את התוצאה שאתה מצפה לה.

אחרי שניסית לפתור לבד אתה מוזמן להציץ בפתרון:

def is_palindrome(s):
  """
  Determines if a string is a palindrome.

  Args:
    s: The string to check.

  Returns:
    True if the string is a palindrome, False otherwise.
  """

  # Create a stack to store the characters of the string.
  stack = Stack()

  # Iterate over the characters of the string.
  for c in s:
    # Push the character onto the stack.
    stack.push(c)

  # Iterate over the stack, popping off characters and appending them to a new string.
  reversed_string = ""
  while not stack.is_empty():
    reversed_string += stack.pop()

  # Return True if the reversed string is equal to the original string, False otherwise.
  return reversed_string == s

נבחן את הפונקציה:

strings = ['madam', 'kayak' , '22/2/22', 'no', 'sir']
for s in strings:
   print(f"'{s}' is {'' if is_palindrome(s) else 'not'} a palindrome")

התוצאה:

'madam' is  a palindrome
'kayak' is a palindrome
'22/2/22' is  a palindrome
'no' is not a palindrome
'sir' is not a palindrome

הפונקציה "is_palindrome" מקבלת מחרוזת כקלט ומחזירה ערך בוליאני. True אם המחרוזת היא פלינדרום, ו-False אם לא. הפונקציה עובדת על ידי יצירת ערימה stack אשר מאחסנת את התווים של המחרוזת. התווים מאוחסנים לפי סדר אחד מעל לשני בערימה, כאשר מגיעים לתו האחרון במחרוזת, הפונקציה מסירה את הפריטים בסדר ההפוך, ומוסיפה כל תו שהיא מסירה למחרוזת חדשה "reversed_string". את המחרוזת ההפוכה היא משווה למחרוזת המקורית. תוצא השוואה זו היא הפלט שהפונקציה מפיקה.

חשוב לציין שדרכים יעילות הרבה יותר לזיהוי פלינדרומים בפייתון משתמשות בפונקציות הפנימיות של השפה שהם תמיד הרבה יותר מהירות:

# Use the ::-1 slice syntax to reverse the string
print(input == input[::-1]) # True

אפשר גם:

# 1. Use the reversed() function
# makes a list out of the string then reverses it
# 2. then join the reversed list back together to a string
print(input == "".join(reversed(input))) # True

כיצד להשתמש ב-Stack לזיהוי האם הסוגריים בביטוי הם מאוזנים?

אחת הדרכים בהם עורכי טקסט ו-IDE למיניהם עוזרים למתכנתים היא בכך שהם מתריאים במידה והסוגריים אינם מאוזנים בקוד שאנחנו כותבים. סוגריים מאוזנים משמעותם שכל סוגר פותח יש לו גם סוגר מאותו סוג שסוגר אותו. לדוגמה:

[(a + b) * c]

הוא ביטוי שבו הסוגריים מאוזנים.

לעומת זאת הביטוי:

(a + b) * c)

הוא דוגמה למקרה בו הסוגריים אינם מאוזנים.

המשימה היא לכתוב קוד המבוסס על הקלאס Stack אותו כתבנו לעיל שיצליח לזהות עבור ביטוי שניתן לו כקלט האם הסוגריים בו הם מאוזנים אם לאו.

אתה מוזמן לנסות לבד.

זה הפתרון שאני מציע, אתה מוזמן להציץ בו אחרי שתנסה לפתור לבד:

def is_valid_bracketing(s):
    """Checks if the input string has balanced brackets.

    Args:
        s: The input string to be checked.

    Returns:
        True if the brackets are balanced, False otherwise.
    """
    
    open_brackets = "([{"
    close_brackets = ")]}"

    # Stack to store unclosed opening brackets
    stack = []
    
    # Iterate over each character in the string
    for c in s:
        # If the character is a closing bracket
        if c in close_brackets:
            # Check if there's an opening bracket to match
            if len(stack) == 0:  
                # Unmatched closing bracket
                return False
            # Check if the brackets match
            elif open_brackets.index(stack[-1]) != close_brackets.index(c):  
                # Mismatched bracket forund
                return False
            else:
                # Matching bracket found, remove from stack
                stack.pop()
        # If the character is an opening bracket, push it onto the stack
        elif c in open_brackets:  
            # Only append open brackets
            stack.append(c)
            
    # If the stack is empty, all brackets are matched
    return len(stack) == 0

נבדוק:

# Test cases

str1 = 'a{b}=[c]'
print(str1, is_valid_bracketing(str1))  # Output: True

str2 = 'a*b{(c(}'
print(str2, is_valid_bracketing(str2))  # Output: False

str3 = '[1{(2)}]'
print(str3, is_valid_bracketing(str3))  # Output: True

str4 = 'x[1{)}]'
print(str4, is_valid_bracketing(str4))  # Output: False

str5 = '3=[[4]}'
print(str5, is_valid_bracketing(str5))  # Output: False

str6 = '3={[4-1]}'
print(str6, is_valid_bracketing(str6))  # Output: True

str7 = '{'
print(str7, is_valid_bracketing(str7))  # Output: False

str8 = '}'
print(str8, is_valid_bracketing(str8))  # Output: False

str9 = ''
print(str9, is_valid_bracketing(str9))  # Output: True

נסביר:

ה-Stack, שבמקרה זה הוא רשימה פייתונית, מאחסן את הסוגריים הפותחים. בכל פעם שהפונקציה מזהה סוגר פותח ")]}" היא מוסיפה אותו לראש הערימה. בכל פעם שהפונקציה מזהה סוגר מסיים "([{" הסוגר הפותח המקביל מוסר מראש הערימה. אם הערימה ריקה כאשר הפונקציה מסיימת לעבור על כל הביטוי, המסקנה היא שהסוגריים מאוזנים. אם הערימה stack אינה ריקה אז הסוגריים אינם מאוזנים.

יעילות משך הביצוע O(N) נובעת מזה שהפונקציה עוברת על כל תו במחרוזת שאורכה N פעם אחת, ועל כל תו היא מבצעת פעולות שמשך הביצוע שלהם קבוע O(N) כך שסך כל קומפלקסיות הזמן היא O(N) * O(1) = O(N).

יעילות האחסון היא גם כן O(N) בגלל שבמקרה הכי גרוע, בו המחרוזת מורכבת כולה מסוגריים פותחים, אורך ה-Stack יהיה N.

נוכל להשתמש בפונקציה לפתרון מגוון בעיות, דוגמת:

• וידוא ביטוי מתמטי
• פרסינג של מסמכי XML ו-JSON
• בדיקה של קוד מחשב

שימוש ב-stack בשביל להמיר מספר לייצוגו הבינארי

אחד האלגוריתמים המשמש להמרת מספר עשרוני לייצוג הבינארי שלו היא לחלק ב-2, לזכור את השארית ואת מנת החלוקה לחלק שוב ב-2. חוזרים על התהליך עד שמגיעים למנת חלוקה 0. אחרי שמסיימים לחלק, מחברים יחדיו את השאריות למחרוזת המבטאת את הייצוג הבינארי.

לדוגמה, נהפוך את המספר 25 לייצוגו הבינארי.

צעד 1: נחלק את המספר 25 ב-2 ונרשום לעצמנו את מנת החלוקה ואת השארית:

25 ÷ 2 = 12 remainder 1

צעד 2: נחלק את מנת החלוקה מהצעד הקודם ב-2 ונרשום לעצמנו את מנת החלוקה ואת השארית:

12 ÷ 2 = 6 remainder 0

נחזור על 2:

6 ÷ 2 = 3 remainder 0

נחזור על 2:

3 ÷ 2 = 1 remainder 1

נחזור על 2:

1 ÷ 2 = 0 remainder 1

צעד 3: אין לנו אפשרות יותר לחלק כי מנת החלוקה היא 0 אז נחבר את השאריות מהצעדים הקודמים מהסוף להתחלה:

11001

נסכם את האלגוריתם להפיכת מספר לייצוגו הבינארי:

1. נחלק מספר ב-2 ונרשום את מנת החלוקה quotient ואת השארית remainder (שהיא בהכרח 0 או 1)
2. נחזור על חלוקה ב-2 עד שנקבל מנת חלוקה שהיא 0.
3. נקרא את השאריות מהסוף להתחלה ונחבר מהם את הייצוג הבינארי של המספר.

אפשר לעשות ייצוג בינארי באמצעות stack בגלל התכונה שלו שהוא הופך את הפלט שמזינים אליו.

נסה לכתוב פונקציה המשתמשת ב-stack כדי להמיר מספר לייצוג בינארי.

פתרון אחד לתרגיל מופיע להלן (עדיף להשתמש בו רק אחרי שניסית לפתור בעצמך):

from collections import deque

def int_to_bin(num):
    # Validate the input and if smaller than 1 return 0
    if num < 1: 
        return "0"
    
    # Use stack to save the remainders
    stack = deque()

     # Collect the results to the stack
    while num > 0:
        remain = num%2
        num = num//2
        stack.append(remain)

    # Pop the results one-by-one in reverse order
    output = ''
    while stack:
        current_digit = stack.pop()
        output += str(current_digit)

    # Return a string
    return output

נבחן את הפונקציה:

# test cases
test_cases = [
    [0, 0],
    [13, 1101],
    [414568369, 11000101101011100111110110001]
]

print(f"{'Result'.ljust(10)}{'Expected'.ljust(10)}{'Conclusion'}")
print(f"{'-'*10}{'-'*10}{'-'*10}")
for num, expected in test_cases:
    res = int_to_bin(num)
    conclusion = "😄" if str(res) == str(expected) else "😭"
    print(f"{str(res).ljust(10)}{str(expected).ljust(10)}{conclusion}")
print("Finito Programa")

סיבוכיות הזמן והמקום של הפונקציה הם O(N).

מדריכים נוספים בסדרה ללימוד פייתון

פתרון בעיית הקיטבג knapsack באמצעות תכנות דינמי

אלגוריתם Selection Sort מיון בחירה

אלגוריתם חיפוש בינארי - מהבנה ליישום

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים