שימוש באלגוריתם backtracking גישוש נסוג לפתרון האתגר של N מלכות

אתגר: עליך להציב N מלכות שחמט על לוח שחמט בגודל N×N כך שאף שתי מלכות לא יאיימו אחת על השנייה.

קלט: מספר המלכות, N.

פלט: כל הפתרונות לבעיית N המלכות, המיוצגים כסט של סטים של קואורדינטות.

בלוח שחמט יש 8 שורות ועמודות. אנחנו נסתפק ב-4 בשביל שיהיה קל להסביר אבל הקוד שנפתח יעבוד על כל מספר N של שורות ועמודות.

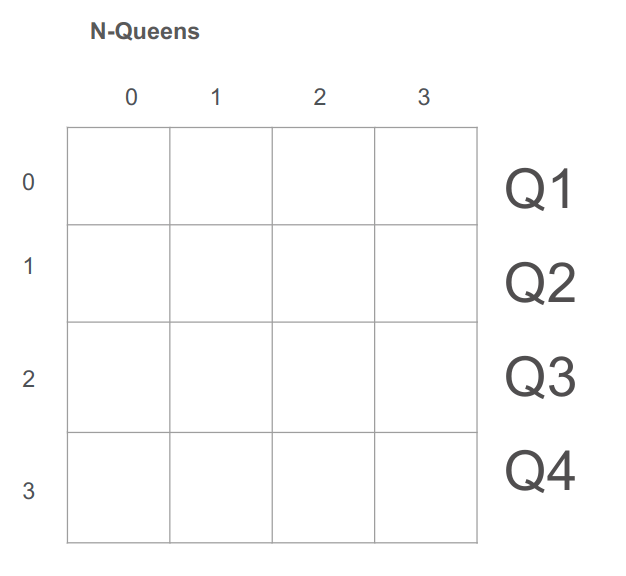
על פי חוקי השחמט אם שמים שתי מלכות באותה שורה או באותה עמודה אז הם יכולות לתקוף אחת את השנייה.

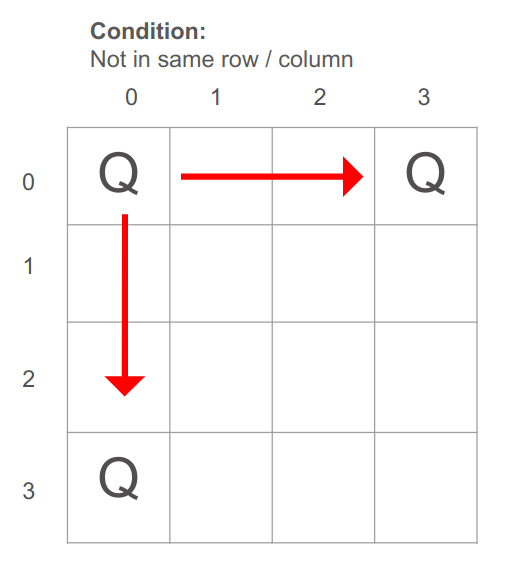
מלכות הנמצאות על אותו אלכסון חיובי גם כן עלולות לתקוף זו את זו.

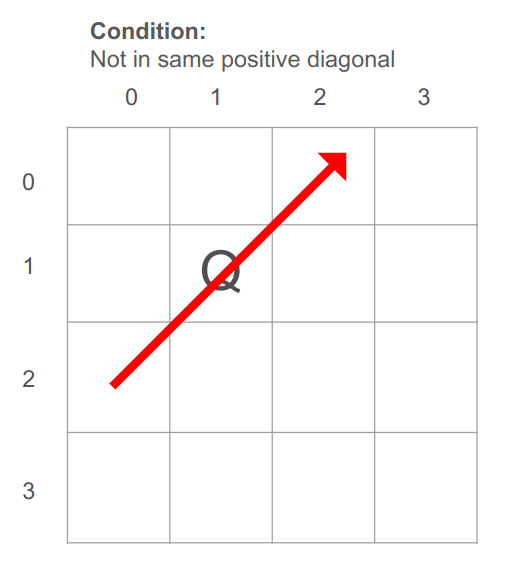
כנ"ל אלכסון שלילי.

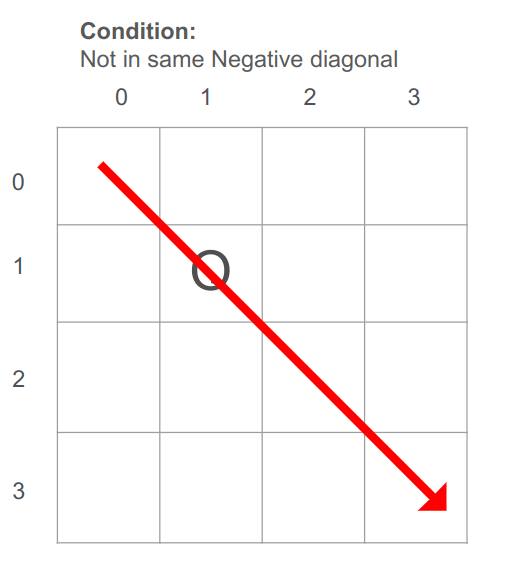
הבעיה היא קומבינטורית ודורשת את כל הפתרונות האפשריים מה שמצביע על אפשרות לפתור אותה באמצעות אלגוריתם backtracking "גישוש נסוג". האלגוריתם מנסה להציב מלכה בכל עמדה על הלוח, שורה אחת בכל פעם. אם המלכה ניתנת להצבה ללא תקיפת מלכות אחרות, האלגוריתם קורא לעצמו באופן רקורסיבי כדי למצוא פתרונות החל מהשורה הבאה. אחרת, האלגוריתם חוזר לאחור ומנסה להציב את המלכה בעמדה אחרת בשורה הנוכחית.

נתחיל מהצבת מלכה בעמדה הראשונה בשורה הראשונה (0,0). נציג את ההצבות על "לוח השחמט" כמו גם באמצעות עץ החלטות:

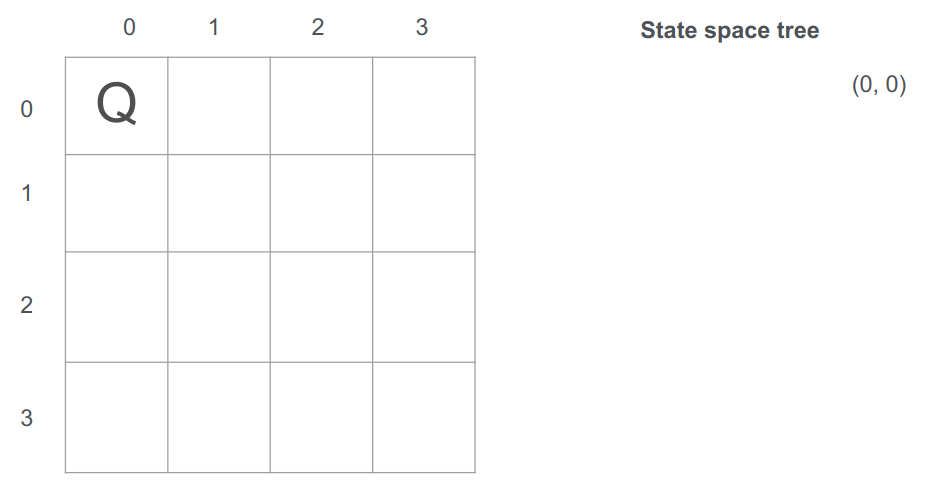
אחרי שמצאנו היכן בשורה הראשונה ניתן להציב מלכה נעבור להציב בשורה הבאה כי אם נשים מלכה נוספת באותה שורה ניתן יהיה להתקיף אותה. נעבור לשורה השנייה:

• עמדה (0,1) חסומה בגלל שלא ניתן להציב 2 מלכות באותה עמודה
• עמדה (1,1) חסומה בגלל שלא ניתן להציב שתי מלכות באותו אלכסון
• ניתן להציב בעמדה (2,1)

מיצינו את השורה השנייה, ונעבור לשלישית:

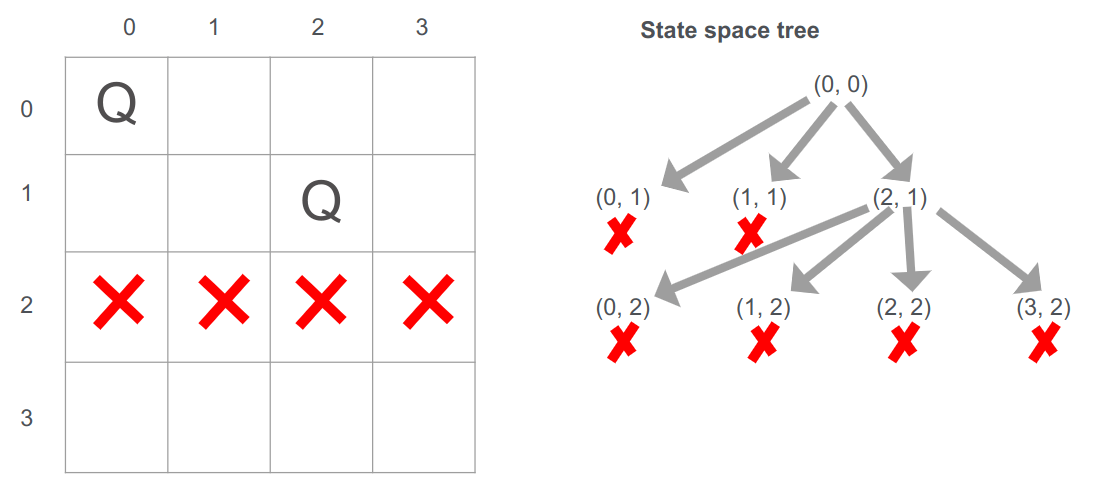
• בשורה השלישית לא ניתן להציב מלכה.

מכיוון שלא ניתן להציב אין לנו ברירה אלא לחזור אחורנית backtrack לשורה שמעל, ושם להגדיר את עמדה (2,1) כמי שלא ניתן להשתמש בה לצורך הפתרון כי שימוש כזה מפר את מגבלות הבעיה.

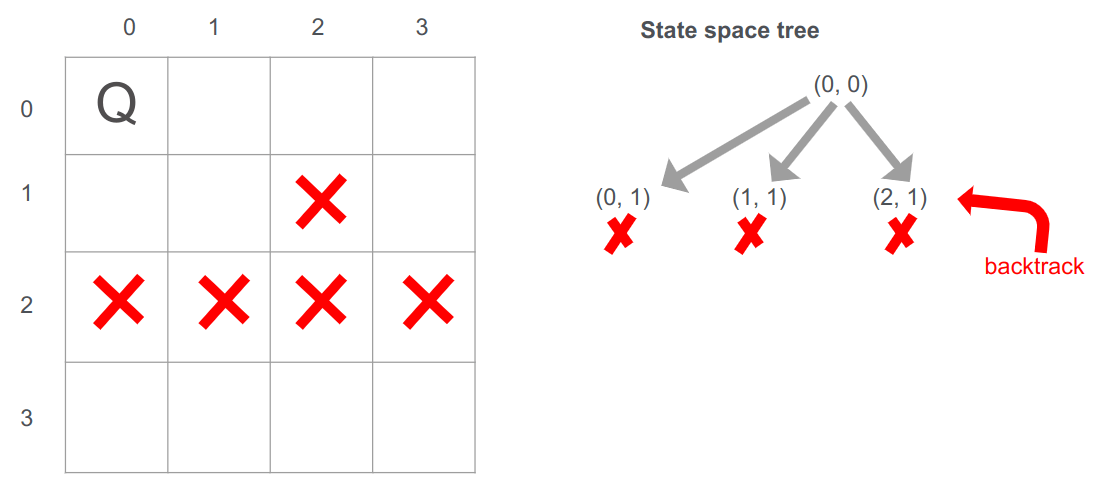
נמשיך לעבור על השורה השנייה ונגיע לעמדה (3,1) שהיא אפשרית אז נציב בה את המלכה.

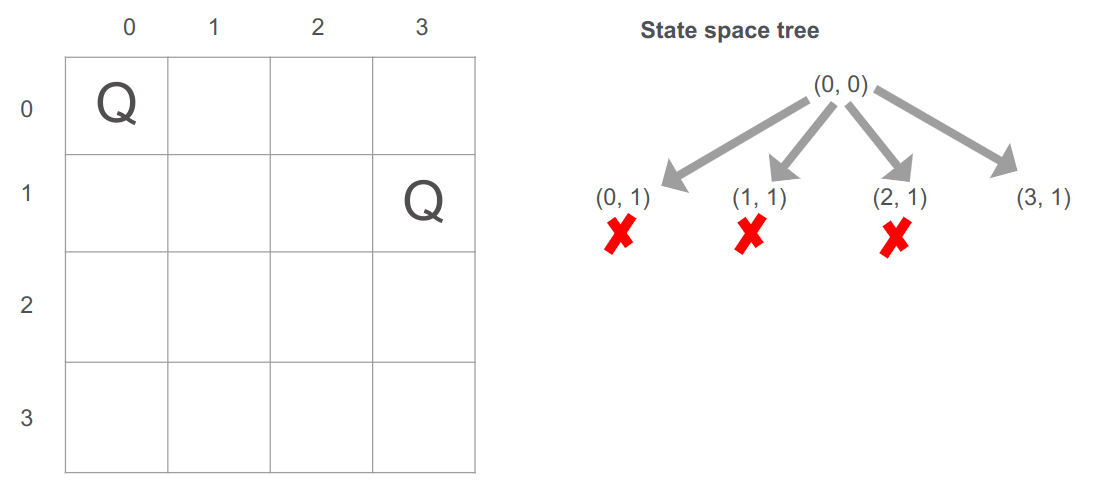
מכיוון שהצבנו בשורה השנייה, נעבור לשורה השלישית:

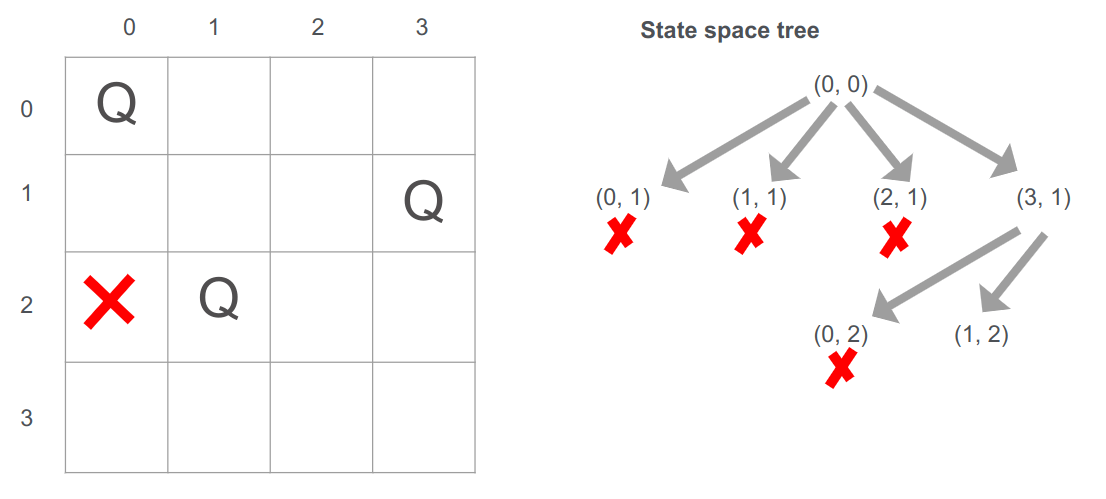
• עמדה (0,2) אינה אפשרית בגלל שהמלכה הראשונה נמצאת באותה עמודה.
• אנחנו כן יכולים להציב את המלכה בעמדה (1,2)

הצבנו מלכה בשורה השלישית, ולכן ננסה להציב בשורה הרביעית:

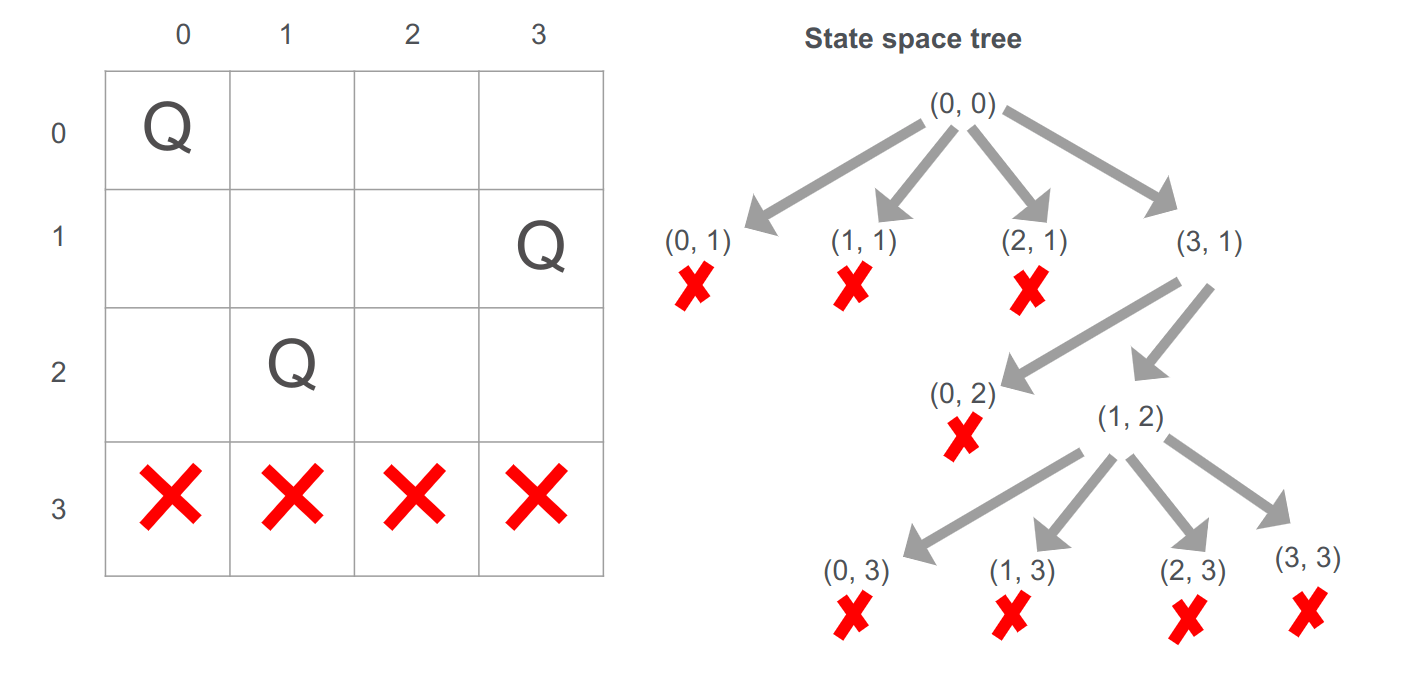
• בשורה הרביעית אי אפשר להציב.

מכיוון שהמצב הנוכחי של המלכה בשורה השלישית אינו אפשרי נחזור על עקבותינו backtrack, ונסמן את הפוזיציה (1,2) כבלתי אפשרית:

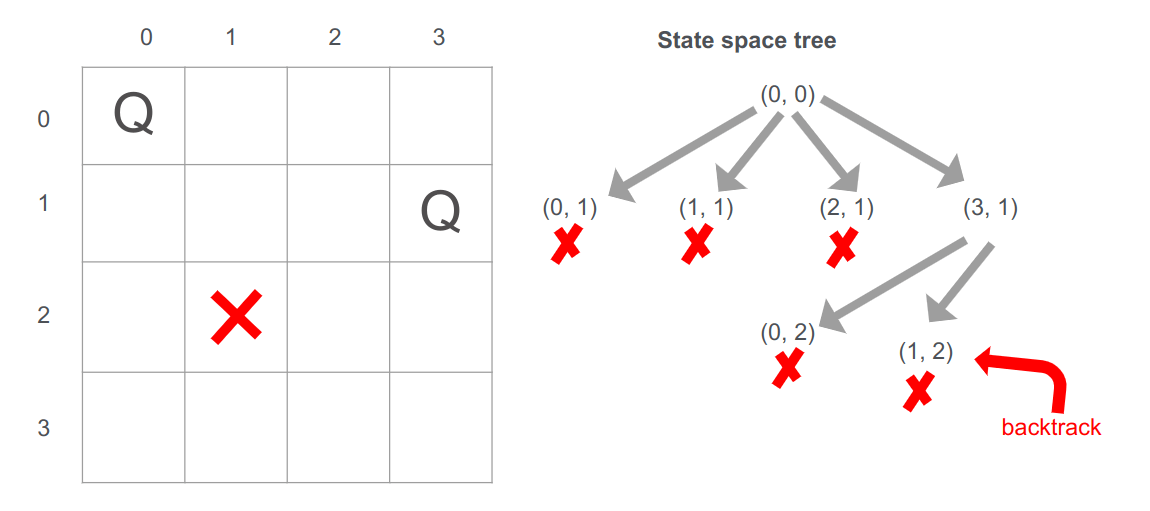
ננסה להציב בתאים הנותרים בשורה השלישית אבל שניהם בלתי אפשריים.

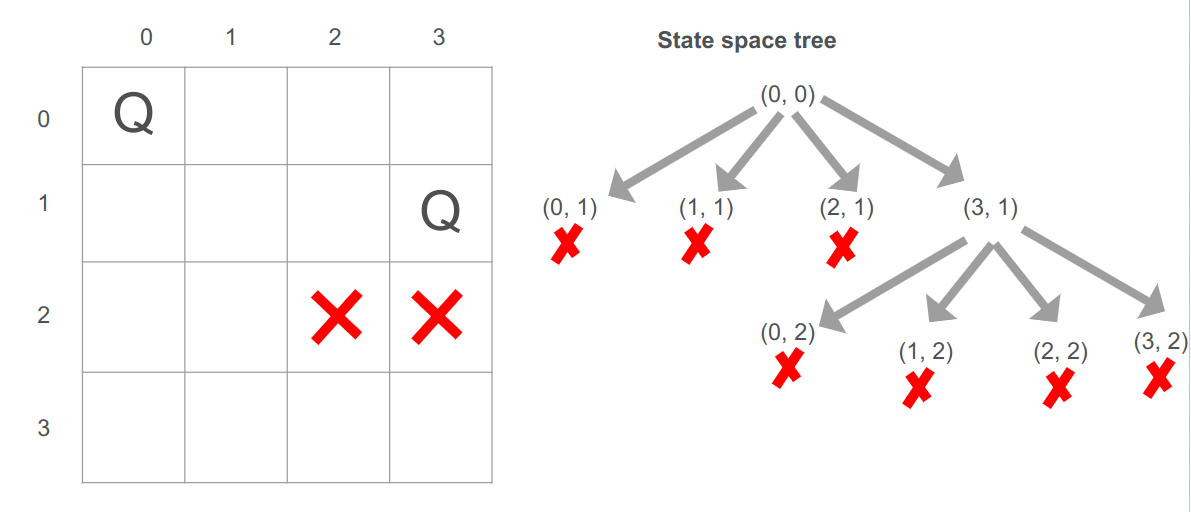
מכיוון שאי אפשר להגיע לפתרון עבור המיצוב הנוכחי של המלכה בשורה השנייה בקואורדינטה (3,1) נחזור על עקבותינו backtrack, ונבטל את המיצוב:

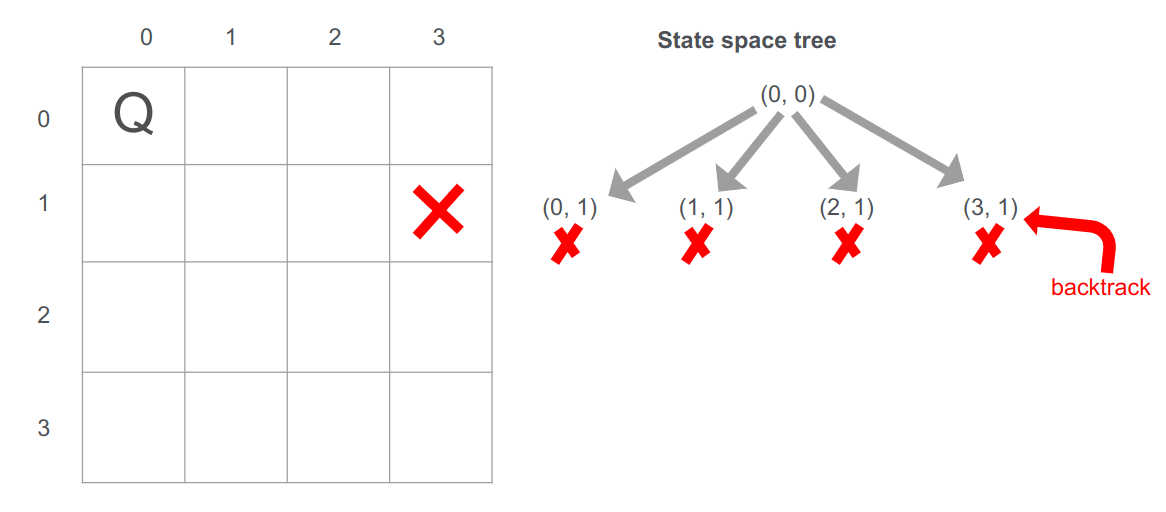
מכיוון שהגענו לסוף השורה השנייה בלי אפשרות למצוא פתרון עבור המצב שבו שמנו את המלכה הראשונה בעמדה (0,0) נחזור על עקבותינו backtrack ונוציא את העמדה מתחום האפשרויות שיכולות להוביל לפתרון:

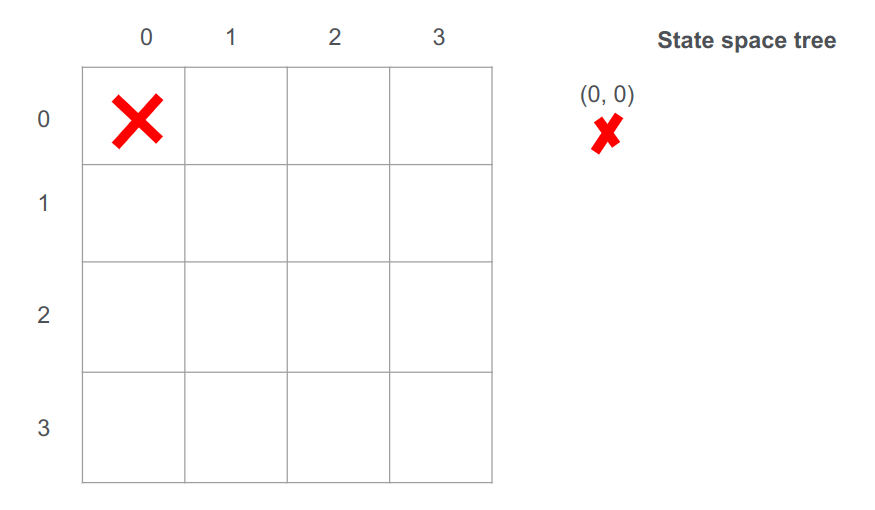
אם לא בעמדה (0,0) אז ננסה בצורה שיטתית בעמדה שמשמאל (1,0):

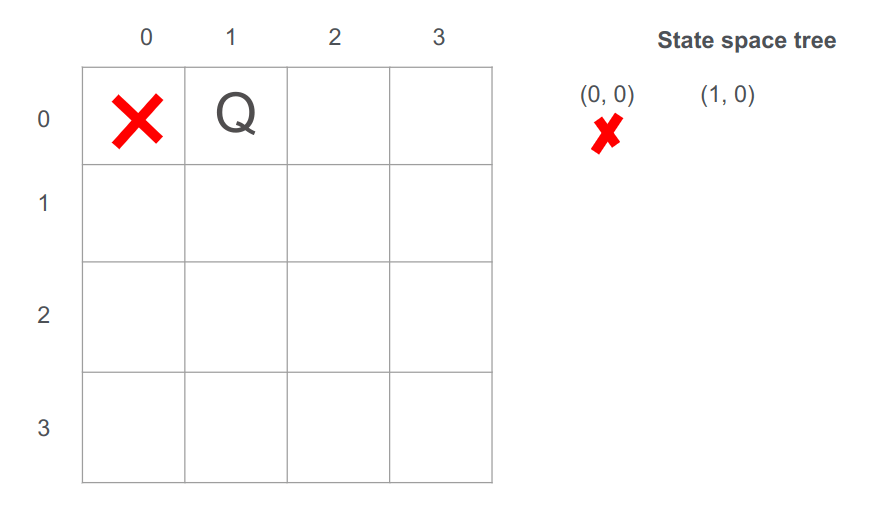
אחרי הצבת המלכה בשורה הראשונה, נעבור לנסות להציב מלכה בשורה השנייה:

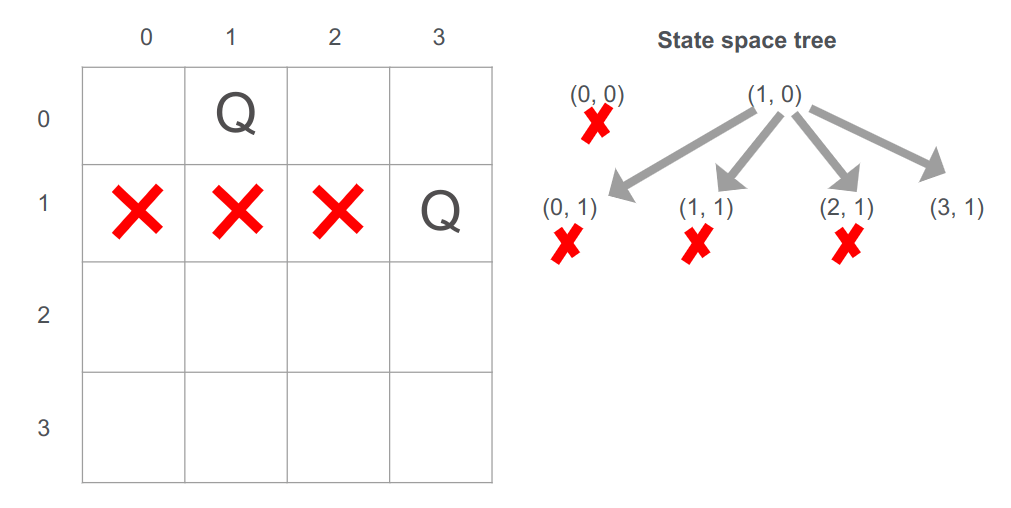
• ניתן להציב את המלכה השנייה רק בעמדה (3,1), וזה מה שעשינו.

אחרי שהצבנו בעמדה (3,1) נרד לשורה הבאה. שם התא הראשון בו ניתן להציב הוא בעמדה (0,2):

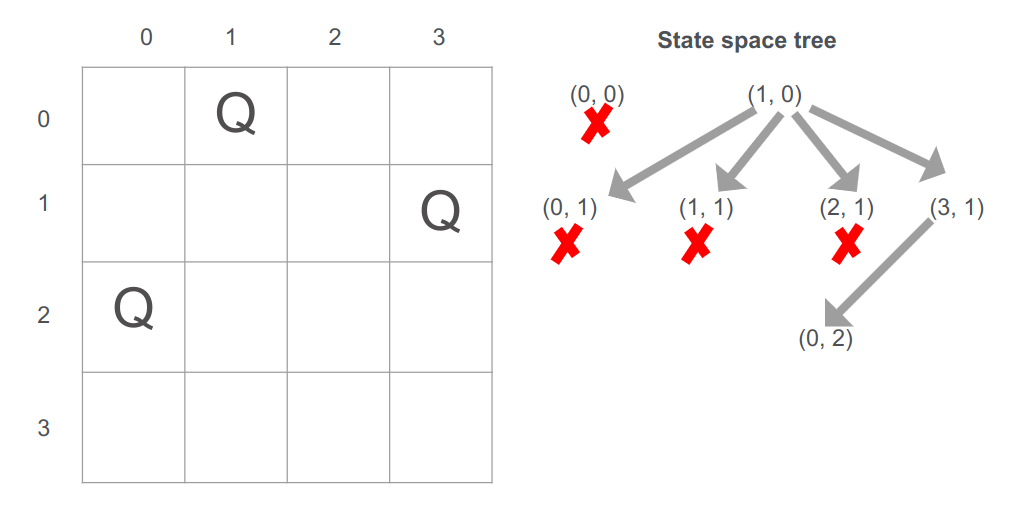
אחרי שהצבנו בשורה השלישית נרד לרביעית:

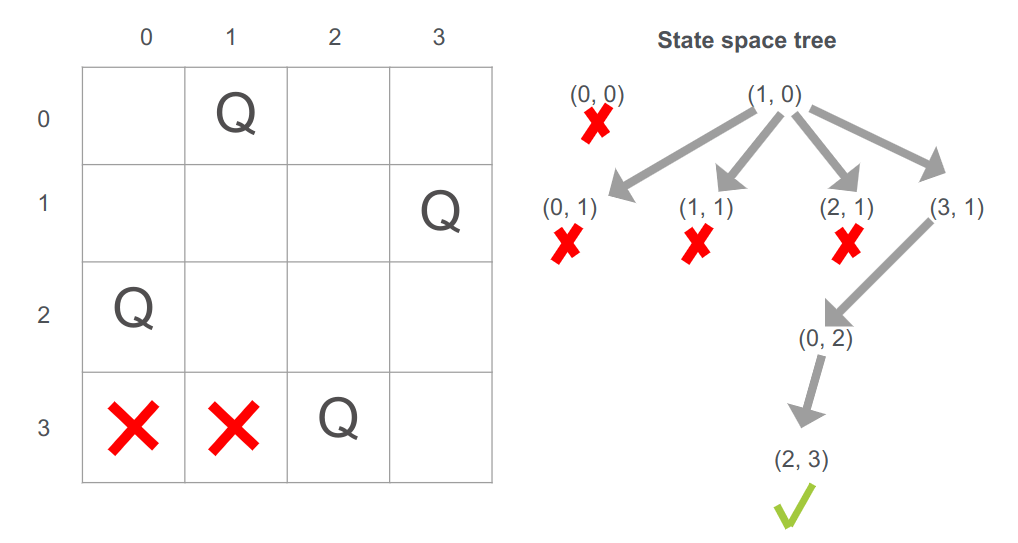
• לא ניתן להציב בשני התאים הראשונים בשורה הרביעית.
• ניתן להציב בתא השלישי של השורה הרביעית.

תם כי הצלחנו להציב 4 מלכות על "לוח השחמט"

אך לא נשלם כי האלגוריתם עדיין צריך למצוא את יתר הקומבינציות של המלכות.

לצורך מציאת יתר הקומבינציות של 4 מלכות האלגוריתם יחזור לאחור backtrack תוך ביטול כל העמדות בכל השורות (שורה רביעית -> שורה שלישית -> שנייה -> ראשונה) בשורה הראשונה הוא יוציא את עמדה (1,0) מתחום הפתרונות האפשריים (כי הוא כבר מיצה אותה לפתרון הראשון שהוא מצא), ואז וינסה למצוא קומבינציה נוספת כאשר מתחילים מהעמדה הבאה משמאל (2,0).

לפני שאנחנו ניגשים לפתור צריך להבין איך למצוא את האלכסונים. לצורך כך נבחין בין אלכסון חיובי לשלילי.

במקרה של אלכסון חיובי, אם נחבר את ערכי X ו-Y של הקואורדינטות על אותו אלכסון יתקבל אותו ערך. נסתכל על התמונה כאשר המלכה היא בעמדה (2,2):

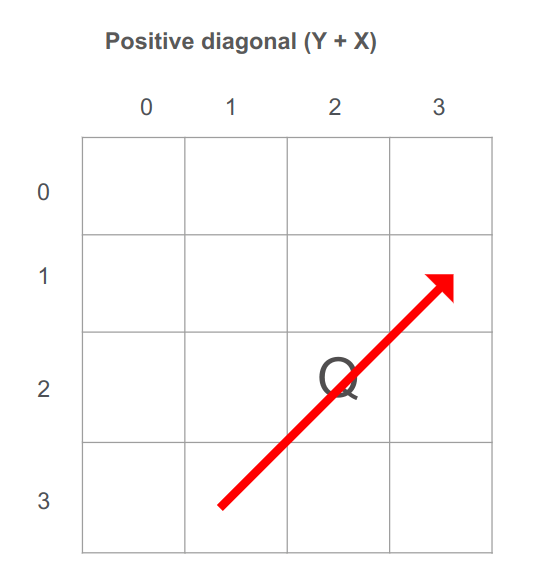
העמדות אשר נמצאות על אותו אלכסון חיובי הם: (2,2) (1,3) (3,1)

נחבר את ערכי ה-X וה-Y של עמדות האלכסון החיובי:

Y + X = 2 + 2 = 4
Y + X = 3 + 1 = 4
Y + X = 1 + 3 = 4

• חיבור ערכי X + Y של כל התאים על אותו אלכסון חיובי נותן את אותו ערך (במקרה זה 4).

הכלל לפיו במקרה של אלכסון חיובי, אם נחבר את ערכי X ו-Y של הקואורדינטות על אותו אלכסון אז יתקבל אותו ערך, תקף עבור כל האלכסונים.

במקרה של אלכסון שלילי, אם נפחית את ערכו של X מ-Y בכל הקואורדינטות על אותו אלכסון יתקבל אותו ערך. נסתכל על התמונה כאשר המלכה היא בעמדה (2,3):

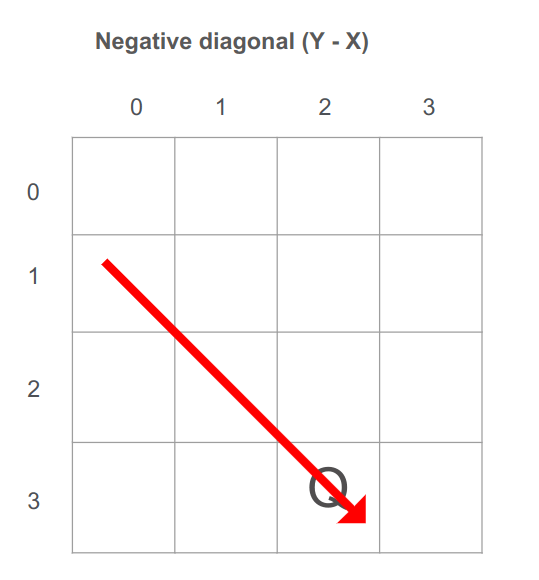
העמדות אשר נמצאות על אותו אלכסון שלילי: (0,1) (1,2) (2,3)

נחסיר את הערך של X מ-Y בכל עמדות האלכסון השלילי:

Y - X = 1 - 0 = 1
Y - X = 2 - 1 = 1
Y - X = 3 - 2 = 1

• חיסור ערכי X מ- Y של כל התאים על אותו אלכסון שלילי נותן את אותו ערך (במקרה זה 1).

הכלל לפיו במקרה של אלכסון שלילי, אם נפחית את ערכו של X מ-Y בכל הקואורדינטות על אותו אלכסון אז יתקבל אותו ערך, תקף עבור כל האלכסונים.

פתרון:

האלגוריתם עובד על ידי ניסיון להציב מלכה בכל עמדה על הלוח, שורה אחת בכל פעם. אם המלכה ניתנת להצבה כי אינה בעמדה לתקוף מלכות אחרות, האלגוריתם קורא לעצמו באופן רקורסיבי כדי למצוא פתרונות החל מהשורה הבאה. אחרת, האלגוריתם חוזר לאחור backtrack ומנסה להציב את המלכה בעמדה אחרת בשורה הנוכחית.

הפונקציה place_n_queens() מקבלת קלט את מספר המלכות, N, ומחזירה סטים של קואורדינטות שפותרים את בעיית הצבת N מלכות.

def place_n_queens(N):
    solutions = set()

הפונקציה is_valid() בודקת אם חוקי להציב מלכה בעמדה הנתונה. היא בודקת האם העמדה כבר תפוסה על ידי מלכה אחרת והאם העמדה עלולה להיות מותקפת על ידי מלכות אחרות:

def is_valid(x, y, placements, pos_diag, neg_diag):
        # Check if it's feasible to place a queen at a specific position
        # by checking diagonals
        if (y+x) in pos_diag or (y-x) in neg_diag:
            return False
        # by checking row and column
        for p_x, p_y in placements:
            if p_x == x or p_y == y:
                return False
        return True

מתוך הפונקציה place_n_queens() ישנו קוד הקורא לפונקציה הפנימית search() שעושה את רוב העבודה. 

הארגומנטים אותם מקבלת הפונקציה search() הם:

• x: קואורדינטת ה-x של העמדה הנוכחית.
• y: קואורדינטת ה-y של העמדה הנוכחית.
• placements: סט של קואורדינטות של המלכות שכבר הוצבו.
• pos_diag: סט של האלכסונים החיוביים תפוסים על ידי מלכות.
• neg_diag: סט של האלכסונים השליליים תפוסים על ידי מלכות.

# Search for new solutions with the backtrack algorithm.
    def search(x=0, y=0, placements=None, pos_diag=None, neg_diag=None):
        # A set of coordinates of the queens that have already been placed.
        if placements is None:
            placements = set()
            
        # A set of the positive diagonals that are occupied by queens.
        if pos_diag is None:
            pos_diag = set()
            
        # A set of the negative diagonals that are occupied by queens.
        if neg_diag is None:
            neg_diag = set()
        
        # Base case: If all queens have been placed successfully, add the current placements to the `solutions` list.
        if len(placements) == N:
            solutions.add(frozenset(placements))
            return

        # Recursive case: Try to place a queen at the next position, and recursively search for solutions from there.
        # 1. Try to place a queen at the next position.
        # 2. If the placement is valid, update the placements, positive diagonals, and negative diagonals.
        # 3. Recursively search for solutions from the next row.
        # 4. Backtrack by removing the queen from the current position.
        for x in range(N):
            if is_valid(x, y, placements, pos_diag, neg_diag):
                # Explore.
                placements.add((x, y))
                pos_diag.add(y+x)
                neg_diag.add(y-x)
                
                # Recursively search solutions for the next row (y + 1).
                search(x, y+1, placements, pos_diag, neg_diag)

                # Backtrack.
                placements.remove((x, y))
                pos_diag.remove(y+x)
                neg_diag.remove(y-x)

הפונקציה search() עובדת באופן הבא:

• אם כל המלכות הוצבו בהצלחה, אז היא מוסיפה את ההצבות הנוכחיות לסט solutions ואז return.
• אחרת, עוברת על כל העמדות האפשריות בשורה הנוכחית.
• עבור כל עמדה, הפונקציה בודקת אם חוקי להציב מלכה בעמדה זו. אם כן, אז היא מציבה את המלכה בעמדה זו וקוראת לעצמה באופן רקורסיבי עבור השורה הבאה של "לוח השחמט".
• לאחר שהקריאה הרקורסיבית מוחזרת, הפונקציה חוזרת אחורה על ידי הסרת המלכה מהעמדה הנוכחית.

לבסוף הפונקציה place_n_queens() מחזירה את סט כל הפתרונות האפשריים, solutions.

להלן הקוד המלא של הפונקציה place_n_queens():

def place_n_queens(N):
    """
    Find all solutions to the N queens problem.

    Args:
        N: The number of queens.

    Returns:
        A set of sets of coordinates, where each set represents a solution to the N queens problem.
    """
    solutions = set()

    def is_valid(x, y, placements, pos_diag, neg_diag):
        # Check if it's feasible to place a queen at a specific position
        # by checking diagonals
        if (y+x) in pos_diag or (y-x) in neg_diag:
            return False
        # by checking row and column
        for p_x, p_y in placements:
            if p_x == x or p_y == y:
                return False
        return True
    
    # Search for new solutions with the backtrack algorithm.
    def search(x=0, y=0, placements=None, pos_diag=None, neg_diag=None):
        # A set of coordinates of the queens that have already been placed.
        if placements is None:
            placements = set()
            
        # A set of the positive diagonals that are occupied by queens.
        if pos_diag is None:
            pos_diag = set()
            
        # A set of the negative diagonals that are occupied by queens.
        if neg_diag is None:
            neg_diag = set()
        
        # Base case: If all queens have been placed successfully, add the current placements to the `solutions` list.
        if len(placements) == N:
            solutions.add(frozenset(placements))
            return

        # Recursive case: Try to place a queen at the next position, and recursively search for solutions from there.
        # 1. Try to place a queen at the next position.
        # 2. If the placement is valid, update the placements, positive diagonals, and negative diagonals.
        # 3. Recursively search for solutions from the next row.
        # 4. Backtrack by removing the queen from the current position.
        for x in range(N):
            if is_valid(x, y, placements, pos_diag, neg_diag):
                # Explore.
                placements.add((x, y))
                pos_diag.add(y+x)
                neg_diag.add(y-x)
                
                # Recursively search solutions for the next row (y + 1).
                search(x, y+1, placements, pos_diag, neg_diag)

                # Backtrack.
                placements.remove((x, y))
                pos_diag.remove(y+x)
                neg_diag.remove(y-x)

    search()
      
    return solutions

הפונקציה הבאה תדפיס את התוצאה:

def print_solutions(sets) :
    """
    Print all of the solutions to the N queens problem, given as a set of sets of coordinates.

    Args:
        sets: A set of sets of coordinates, where each set represents a solution to the N queens problem.
    """
    grid = ""
    for placements in sets:
        for y, _ in enumerate(range(N)):
            grid += NEW_LINE
            for x, _ in enumerate(range(N)):
                if (x, y) in placements:
                    grid += ' Q '
                else :
                    grid += " - "
        print(grid)
        grid = ""

נבדוק:

# Test case
N = 4 # Change N as needed : 0, 1, 8
print_solutions(place_n_queens(N))

התוצאה:

 -  Q  -  - 
 -  -  -  Q 
 Q  -  -  - 
 -  -  Q  - 

 -  -  Q  - 
 Q  -  -  - 
 -  -  -  Q 
 -  Q  -  -

• הרצת הקוד מציגה את כל ההצבות האפשריות של 4 מלכות על לוח של 4X4.

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

רקורסיה בפייתון - כל מה שרצית לדעת ועוד כמה דברים חשובים

אלגוריתם חיפוש לעומק DFS - מהבנה ליישום

תכנות דינמי מלמטה למעלה ובחזרה - מדריך לתכנות דינאמי שמתחיל מהבסיס

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים