חידה תכנותית: מטריצה ספירלית

בהינתן מטריצה דו-ממדית (רשימה של רשימות) של מספרים שלמים, כתוב פונקציה אשר מחזירה רשימה המכילה את האלמנטים של המטריצה בסדר ספירלי.

דוגמה:

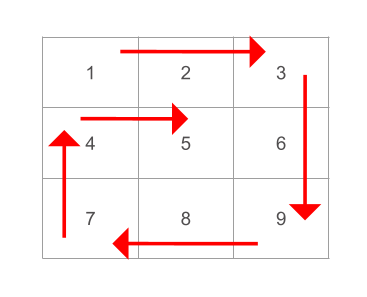
Input: matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
Output: path = [1, 2, 3, 6, 9, 8, 7, 4, 5]

הסבר:

עקוב אחר החיצים החל מהפינה השמאלית העליונה. כל פריט מטריצה שהפונקציה עוברת דרכו צריך להתווסף לנתיב שהפונקציה תחזיר. שים לב שנתיב המעבר יוצר ספירלה שעוברת על כל אחד מהפריטים פעם אחת בדיוק.

אילוצים:

• המטריצה תהיה רשימה של רשימות.
• כל האלמנטים במטריצה יהיו מספרים שלמים.
• אתה יכול להחזיר את האלמנטים בכל סדר כל עוד הם עוקבים אחר דפוס הספירלה.

בונוס:

• אם המטריצה ריקה, החזר רשימה ריקה.

הבהרות:

• המטריצה מתחילה בפינה השמאלית העליונה, הולכת ימינה עד שהיא פוגעת בסוף, ואז פונה כלפי מטה, וכן הלאה.
• יש לעבור על כל אלמנט במטריצה פעם אחת בלבד.

הצעה לפתרון האתגר

def spiral_matrix(matrix):
    """Traverses a matrix in a spiral pattern and returns the path."""
    
    # Initialize an empty list to store the traversal path.
    path = []
    
    # Handle the case of an empty matrix.
    if not matrix:
        return path
    
    # Get the dimensions of the matrix.
    len_row, len_col = len(matrix), len(matrix[0])
    
    # Initialize cursors to track boundaries.
    top = 0
    left = 0
    bottom = len_row
    right = len_col
    
    # Initialize the starting position coordinates
    y, x = 0, 0

    # Loop until the horizontal or vertical cursors meet.
    while left < right and top < bottom:
        # Move rightwards and append elements to the path.
        for x in range(left, right):
            path.append(matrix[y][x])
        top +=  1
        
        # Move downwards and append elements to the path.
        for y in range(top, bottom):
            path.append(matrix[y][x])
        right -= 1
        
        # Check if the cursors have met before continuing.
        if left >= right or top >= bottom:
            break
        
        # Move leftwards and append elements to the path.
        for x in range(right-1, left-1, -1):
            path.append(matrix[y][x])
        bottom -= 1
        
        # Move upwards and append elements to the path.
        for y in range(bottom-1, top-1, -1):
            path.append(matrix[y][x])
        left += 1
    

    return path

נבחן את הפונקציה:

# Test cases

test_cases = []

matrix = [
   [1, 2, 3],
   [4, 5, 6],
   [7, 8, 9]
]
test_cases.append([matrix, [1, 2, 3, 6, 9, 8, 7, 4, 5]]) 

matrix = [
 [1, 2,  3,  4],
 [5, 6,  7,  8],
 [9, 10, 11, 12]
]
test_cases.append([matrix, [1, 2, 3, 4, 8, 12, 11, 10, 9, 5, 6, 7]]) 

matrix = [
 [1,  2,  3,  4,  5],
 [6,  7,  8,  9,  10],
 [11, 12, 13, 14, 15],
 [16, 17, 18, 19, 20]
]
test_cases.append([matrix, [1, 2, 3, 4, 5, 10, 15, 20, 19, 18, 17, 16, 11, 6, 7, 8, 9, 14, 13, 12]]) 

matrix = [
 [1,  2,  3,  4,  5]
]
test_cases.append([matrix, [1, 2, 3, 4, 5]]) 

matrix = [
 [1],
 [2],
 [3],
 [4]
]
test_cases.append([matrix, [1, 2, 3, 4]]) 

test_cases.append([[], []]) 

for matrix, expected in test_cases:
    res = spiral_matrix(matrix)
    conclusion = "😄" if res == expected else "😭"
    sign = "==" if res == expected else "!="
    print(f"{conclusion} | {res} {sign} {expected}")

הפונקציה spiral_matrix מקבלת מטריצה כקלט ומחזירה רשימה המכילה את האלמנטים של המטריצה בסדר ספירלי.

הפונקציה כוללת את השלבים הבאים:

1. מערך ריק path מאותחל לצורך אחסון נתיב המעבר.

2. אם המטריצה שהוזנה ריקה, הפונקציה מחזירה מיידית מערך ריק.

3. ממדי המטריצה מחושבים באמצעות הפונקציה len. כאשר len_row מאחסן את מספר השורות, ו-len_col מאחסן את מספר העמודות.

4. אתחול סמנים:

• ארבעה סמנים (top, left, bottom, ו-right) מאותחלים כדי לעקוב אחר גבולות המעבר הספירלי.

• בתחילה, top ו-left מוגדרים ל-0, bottom נקבע למספר השורות, ו-right נקבע למספר העמודות.

5. אתחול המיקום ממנו מתחיל המעבר:

• שני משתנים y ו-x מאותחלים ל-0, ומייצגים את קואורדינטות מיקום ההתחלה במטריצה.

6. מעבר על המטריצה בסדר ספירלי:

• הפונקציה עוברת על המטריצה בתוך לולאת while.

• הלולאה ממשיכה לרוץ כל עוד הסמנים האופקיים (left ל-right) והאנכיים (top ל-bottom) לא נפגשו.

• בכל פעם שהלולאה רצה:

• הפריט הנוכחי מתווסף למערך path.

• תנועה ימינה מהסמן השמאלי ועד הימני מוסיפה ע"פ סדר את פריטי השורה העליונה ביותר שעדיין זמינה. בסופה של התנועה מקדמים את הסמן העליון שורה אחת למטה כדי למנוע אפשרות למעבר נוסף על השורה העליונה הנוכחית.

• תנועה למטה מהסמן העליון ועד התחתון מוסיפה ע"פ סדר את פריטי העמודה הימנית ביותר שעדיין זמינה. בסופה של התנועה מסיגים את הסמן הימני עמודה אחת לשמאל כדי למנוע אפשרות למעבר נוסף על העמודה הימנית הנוכחית.

• תנועה שמאלה מהסמן השמאלי ועד לימני מוסיפה ע"פ סדר את פריטי השורה התחתונה ביותר שעדיין זמינה. בסופה של התנועה מסיגים את הסמן התחתון מקום אחד כלפי מעלה כדי לחסום את המעבר על השורה התחתונה הנוכחית.

• תנועה למעלה מהסמן התחתון ועד לעליון מוסיפה ע"פ סדר את פריטי העמודה השמאלית ביותר שעדיין זמינה. בסופה של התנועה, מקדמים את הסמן השמאלי מקום אחד לימין כדי לחסום את המעבר על העמודה השמאלית הנוכחית.

• הלולאה מסיימת לרוץ כאשר הסמנים נפגשים או חוצים.

7. לאחר סיום הריצה של הלולאה, ולאחר מעבר על כל אחד מהפריטים בדיוק פעם אחת, הפונקציה מחזירה את המערך path אשר מכיל את פריטי המטריצה בסדר ספירלי.

ניתוח ביצועים

סיבוכיות זמן:

הקוד עובר על כל פריט של המטריצה בדיוק פעם אחת, ולפיכך עבור מטריצה שממדיה m ו-n סיבוכיות הזמן היא O(m * n).

סיבוכיות מרחב:

הפונקציה דורשת מקום נוסף כדי לאחסן בזיכרון את הפריטים של המערך path שמכיל בתוכו מספר של m*n פריטים, כמספר הפריטים במטריצה.

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

שימוש בטכניקות שני המצביעים לפתרון בעיות תכנותיות

טכניקת חלון ההזזה sliding window לפתרון בעיות ברצפים

רקורסיה בפייתון - כל מה שרצית לדעת ועוד כמה דברים חשובים

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים