איך שוב לא תיפול בפח הסטטיסטיקה - על כשלים סטטיסטיים ועל פתרונם

רק השבוע בישר ראש ממשלתה של מדינה קטנה על כך שרוב הציבור במדינה תומך בדעתו. באמירתו הוא שכח לציין מה השאלות שנשאלו בסקר, מה היה גודל המדגם והאם הוא מייצג, ושאלת השאלות, האם לא הספיק לשנות את דעתו מאז. פוליטיקאי זה אינו היחיד המשתמש בסטטיסטיקה בצורה מטעה. בסקירה זו, בכוונתי להביא לידיעת הקוראים תכסיסים נוספים בהם נוקטים בעלי עניין מתוחכמים במטרה לבלבל את הציבור.

הדגימה המוטה

סטטיסטיקה מבוססת על העובדה שלא ניתן לבחון את כל האוכלוסייה ולכן דוגמים קבוצה קטנה, ובשאיפה מייצגת, וממנה מסיקים לגבי כלל האוכלוסייה. בעיה אחת היא שהמדגם צריך להיות מייצג ולשם כך הוא צריך להיות אקראי כמה שניתן וגדול מספיק.

ניקח את הדוגמה של ספרנית העורכת מחקר על הרגלי שעות הפנאי של סטודנטים, ולשם כך מחלקת שאלונים בין פוקדי הספרייה במוסד ללימודים גבוהים שבו היא עובדת. אם הספרנית תסתפק בשאלונים אותם חילקה במקום עבודתה היא תפספס את כל אותם סטודנטים שלא טרחו להגיע לספרייה, התוצאות שלה יהיו מבוססות על דגימה לא מייצגת, וסביר שמסקנותיה לא יצליחו לענות על שאלות המחקר.

בנוסף, דגימה עלולה להיות לא מייצגת פשוט מפני שהיא קטנה מדי. לקחתי מטבע בלתי מוטה של 10 שקלים שהיה אצלי בארנק וזרקתי אותו 10 פעמים, ומה שקיבלתי היה יחס של 7:3 בין "ראש" ל"זנב" במקום 5:5 הצפוי. כדי לחסוך מעצמי את הצורך לזרוק יותר פעמים השתמשתי בתוכנת מחשב שרצה אונליין כדי לדמות 100 זריקות. שם התוצאות היו 51:49. קרובות יותר ליחס הצפוי של 50:50. ניסוי קצר זה מלמד שדגימה קטנה מדי נוטה שלא לייצג נאמנה את האוכלוסייה.

כאשר אתה נתקל בתוצאות מחקר, משאל או מדגם המתפרסמות חדשות לבקרים, תנסה לשים לב לשיטה שבה נאספו הנתונים. כמה משתתפים היו במחקר ואיך נאספו הנתונים מה שיאפשר לך להעריך האם הדגימה היא מוטה או מייצגת מספיק.

קטיף דובדבנים: בחירה סלקטיבית של נתונים במדע ובחיים

"קטיף דובדבנים" הוא מונח המתאר את הנטייה לבחור מידע שמאשש טענה מסוימת תוך התעלמות ממידע שסותר אותה. זה דומה לחקלאי הקוטף רק את הדובדבנים היפים ביותר ומשאיר את הפחות מוצלחים על העץ.

בשנות השישים של המאה ה-20, חוקרים מובילים בתחום התזונה פרסמו מאמר שסקר מחקרים על הקשר בין צריכת שומן במזון ומחלות לב. המאמר בחר להדגיש מחקרים שהראו קשר בין צריכת שומן למחלות לב, אך המעיט בחשיבותם של מחקרים שהצביעו על נזקי הסוכר. למרות שפרסום זה נתקל בביקורת נחרצת כבר במועד פרסומו, הוא השפיע רבות על המדיניות התזונתית של הדורות הבאים. כיום, מחקרים רבים מראים שהסוכר – ולא השומן – הוא גורם מרכזי למחלות לב.

האם המסקנות שפורסמו אז הושפעו מהקשר בין החוקרים לתעשיות מזון? קיימות עדויות לכך שתעשיית הסוכר מימנה חלק מהמחקרים, מה שייתכן והשפיע על הממצאים. דוגמה זו ממחישה את הסיכון שבבחירה סלקטיבית של נתונים והצורך בביקורתיות תמידית.

לא רק במדע מתרחש "קטיף דובדבנים". גם דרשנים דתיים נוטים להשתמש בסיפורי ניסים כשהם מעוניינים למכור את מרכולתם. ההסבר הוא כמובן פשוט יותר ואינו מצריך "ניסים" אלא מעט הבנה בהסתברות. בהתחשב בכמות האדירה של אירועים המתרחשים לכל האנושות המונה מיליארדים בכל יום, הרי זה הכרח שחלקם הקטן יהיו כל כך יוצאי דופן, עד שיהיה מי שישמח לפרסם אותם כהתערבות על-טבעית.

מה אפשר ללמוד מזה? "קטיף דובדבנים" מזיק לאיכות המידע שאנו צורכים, שכן הוא יוצר תמונה מעוותת של המציאות. התהליך המדעי נועד לחשוף טעויות ולהסיר מידע שגוי, אך התופעה קיימת גם בתחומים שבהם התיקון אינו חלק מובנה מהתהליך. לכן, חשוב לשמור על גישה ביקורתית ולבחון את כל מקורות המידע הזמינים לפני קבלת החלטות משמעותיות.

באיזה מדד אמצע להשתמש

ישנה מעשייה על סניף בנק שבו ממוצע השכר הוא קצת יותר מחצי מיליון ש"ח כאשר מביאים בחשבון את שכרו של המנהל שמרוויח 5 מיליון ש"ח ואת שכרם של 9 הפקידים שכל אחד מהם מרוויח רק 10,000. מעשייה זו מדגימה כיצד שימוש בממוצע עלול להטעות.

הבעיה נובעת מההרגל האנושי להשתמש בממוצע היות ופשוט לחשבו והוא מיטיב לתאר תופעות טבעיות רבות. זוכר את עקומת ההתפלגות הנורמלית מימי בית הספר?

היא מייצגת התפלגות דמויית פעמון שבה הממוצע נמצא בדיוק באמצע כאשר כל התצפיות מתפלגות סביב האמצע, וככל שאנו מתרחקים מהאמצע כך קטן הסיכוי למצוא דוגמה מייצגת. לדוגמה, הגובה הממוצע של גברים ישראלים הוא 175 ס"מ. גובהם של כמעט 70% מהגברים נע בין 170 ל-180 ס"מ, רק 7.5% יהיו גבוהים מ-185 ס"מ ורק אחד לאלף יהיה גבוה מ-2 מטר. ההתפלגות הנורמלית מתארת מצוין תופעות טבעיות דוגמת גובה של אנשים.

הבעיה מתחילה כשמנסים לתאר תופעות שהם תוצר של חברה אנושית. לדוגמה, השווי הכולל של האמריקאי הממוצע הוא 300,000$. תוסיף למדגם את אלן מאסק, האיש העשיר בעולם ששוויו 100 מיליארד דולר, והממוצע קופץ ל-100,297,000$. דוגמה יחידה שהקפיצה את הממוצע ב-33,432%. זה מפני שתופעות אנושיות, דוגמת חלוקת העושר בעולם, מחירי דירות, מספר הקוראים של ספר, וגם מספר העוקבים ברשת החברתית X אינם מתנהגים בהתאם להתפלגות הנורמלית בגלל שיש גבול לכמה נמוך אפשר לרדת (לא ניתן למכור פחות מאפס עותקים של ספר) אבל אין גבול לכמה שניתן לעלות.

דרך אחת להתמודד עם ההטייה שבשימוש בממוצע על נתונים שאינם מתפלגים באופן נורמלי היא שימוש בחציון. החציון לוקח את הערך האמצעי שנמצא בדיוק באמצע בין התוצאות הגבוהות לנמוכות. תתאר לעצמך 100 אמריקאים עומדים בשורה אחת שבה האנשים ממויינים לפי שווים. הראשון בשורה הוא העני ביותר, והאחרון הוא העשיר ביותר. מה שמעניין אותך לצורך אמידת החציון הוא שוויו של האדם במקום ה-50, באומדן זה תשתמש לתיאור האוכלוסייה באופן בלתי מוטה במקום בממוצע.

לסיכום, שימוש בחציון במקום בממוצע כמדד אמצע עבור נתונים שאינם מתפלגים נורמלית חוסך מאיתנו את העיוות של התוצאות הנגרם בגלל הרגישות של הממוצע לערכים קיצוניים.

הצגת נתונים בדרך מטעה ושגיאות בהסקת מסקנות

זוג התאומים אמנון ותמר לומדים ביחד באותה כיתה. במבחן במתמטיקה תמר קיבלה ציון 87 ולעומתה אמנון קיבל רק 81. ההורים החרדים ממהרים להתקשר למחנכת הכיתה שמיידעת אותם שהציון הממוצע של הכיתה בבחינה היה 84 כאשר הנתונים מתפלגים באופן נורמלי. ההורים משבחים את התלמידה המחוננת שגדלה להם בבית, ולא מצליחים להסתיר את מורת רוחם מהבן הלא יוצלח.

האם ההורים צודקים בגישתם?

מבחינה מתמטית ההורים פספסו מידע קריטי להבנת הציון שהוא סטיית התקן. כאשר סטיית תקן מודדת את הפיזור סביב הפרמטר כאשר ככל שהסטייה גדולה יותר כך גדל הפיזור. במקרה של זוג התאומים שאתרע מזלם ללמוד באותה כיתה, אם סטיית התקן היא 10 נקודות אז הציון הנכון של אמנון ינוע היכן שהוא בין 71 ל-91, והציון של תמר יימצא בטווח שבין 77 ל-97. מה שאומר שיש חפיפה בין התוצאות. משמע, יכול להיות ששניהם מוכשרים באותה מידה אבל קשה לדעת את זה אם מסתכלים על הממוצע בלבד.

דרך טובה יותר היא להסתכל על טווחים. לדוגמה, בטווח הראשון יהיו תלמידים שקיבלו 90 ויותר. בטווח שמתחתיו יהיו תלמידים שקיבלו בין 80 ל-90, וכיו"ב. בהתאם לגישה זו, ההבדל בין מי שקיבל 70 ל-90 הוא משמעותי כי הציונים מצויים בשכבות שונות אבל כל מי שקיבלו בין 80 ל-90 מצויים באותו טווח, ולכן אינם שונים משמעותית.

המסקנה לכל האנשים המודאגים היא שצריך להסתכל על סטיית התקן כדי להבין טוב יותר את טווח התוצאות ואם רואים שהתוצאה היא בטווח המקובל אז אפשר להירגע.

דרך עיקרית להשוות בין ממוצעים ולאפשר הסקה סטטיסטית היא באמצעות מבחן השערות. במסגרתו לא מספיק ששני גדלים יהיו שונים, צריך גם לבדוק האם ההבדל הוא בעל משמעות סטטיסטית ואם כן באיזו מידה. הרמה המקובלת היא 5%. אבל במקרים מסוימים, נדרוש רמת ביטחון של 1% כדי להיות בטוחים שהבדלים קיימים, ואינם תולדת המקרה.

אפילו אם התוצאות משמעותיות מבחינה סטטיסטית אין למהר ולהסיק מסקנות משום שייתכנו תוצאות משמעותיות סטטיסטית שהם חסרות משמעות מעשית. לדוגמה, מחקר המוצא הבדל משמעותי סטטיסטית של 3 נקודות מתוך 100 לטובת התלמידים שלמדו בשיטה חדישה לעומת הקיימת. האם תוצאה זו מצדיקה את ההשקעה בהכשרת מורים ובהחלפת ספרי הלימוד? זו שאלה שאיתה צריכים להתמודד מקבלי ההחלטות.

חלוקת נתונים לטווחים ולקבוצות היא טכניקה יעילה גם מחוץ למבחנים מתוקננים והוראה בכיתה. כך, לדוגמה, בזמן המלחמה האמריקאית - ספרדית שיעור האבידות בצי של ארה"ב היה 9 הרוגים ל-1,000 כשבאותה תקופה שיעור התמותה בניו יורק היה 16 ל-1,000. מגייסי הצי השתמשו בעובדה זו כדי לעודד צעירים בריאים להתגייס לשורותיהם. האם אתה רואה את הבעיה? מה שהמגייסים עשו היה להשוות בין דברים שאינם ברי השוואה. בה בשעה, שמגייסים לחיל הים גברים צעירים וחסונים, אוכלוסיית ניו יורק מורכבת מאנשים מכל המינים, ובני כל הגילאים, לא כולם בקו הבריאות.

דרך אחת להתמודד עם הבעיה היא באמצעות שיכוב, הפרדה לשכבות (סטרטיפיקציה), אשר מפרידה את הנתונים לקבוצות ברות השוואה. במקרה זה, נכון יותר להשוות אל מול שכבת הגברים הבריאים בני 18-30 המתגוררים בניו יורק כדי להבין היכן יותר בטוח - בעיר הגדולה או בים.

טריק מוכר הוא להשוות את המצב לפני למצב אחרי. קח כדוגמה את הדיאטה התורנית שמישהו מנסה לדחוף לך לצלחת. בפרסומת אתה רואה אישה שמנה ועגמומית בתמונה שמייצגת את המצב לפני הדיאטה, ואישה חייכנית ואטרקטיבית בתמונה שאחרי. בדיקה מעמיקה יותר עשויה לגלות שחוץ מאשר השפעת הדיאטה, אם היתה כזו, המצולמת במצב שאחרי לובשת שמלה שחורה כי ידוע שהצבע השחור מרזה וגם החיוך שנוסף בתמונה שאחרי מוסיף לפרסומת כוח שכנוע. במצב עניינים שכזה קשה להחליט חלקו של מי בשינוי גדול יותר, הסטייליסט או הדיאטה.

המסקנה היא שצריך להיזהר ממידע המוצג באופן מוטה. אתה רואה ממוצע אז תשאל - איזה ממוצע? מי כלול בפנים? מה סטיית התקן? האם ההבדל הוא בעל משמעות סטטיסטית ומעשית? וכאשר מראים לך נתונים של לפני ואחרי תוודא שהם ברי-השוואה.

הגרף המטעה

אמרה ידועה גורסת ש"תמונה שווה אלף מילים". מה שהפתגם שוכח לציין הוא עד כמה תמונה, בייחוד אם היא גרף, עלולה להטעות.

ניקח את הגרף הבא המתאר עלייה של 10% בתוך כשנה:

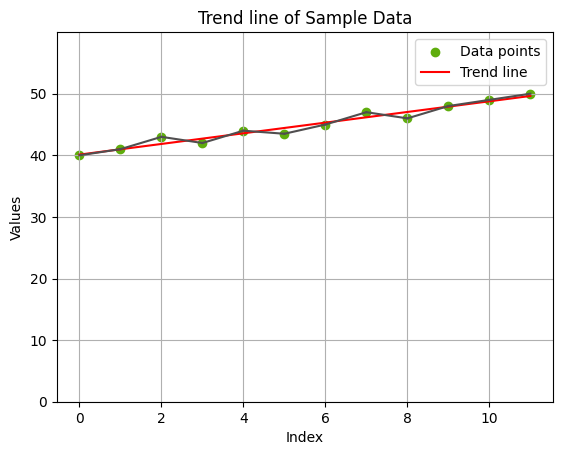
הגרף נראה יפה מאוד אם כל מה שאתה רוצה לעשות הוא לתקשר מידע. אבל בוא נאמר שאתה משווק מתוחכם (או שאתה רוצה לחסוך במקום) ולפיכך אתה מחליט לקצץ את כל חלקו של הגרף שבין הערך 0 לערך ממנו הנתונים מתחילים להשתנות:

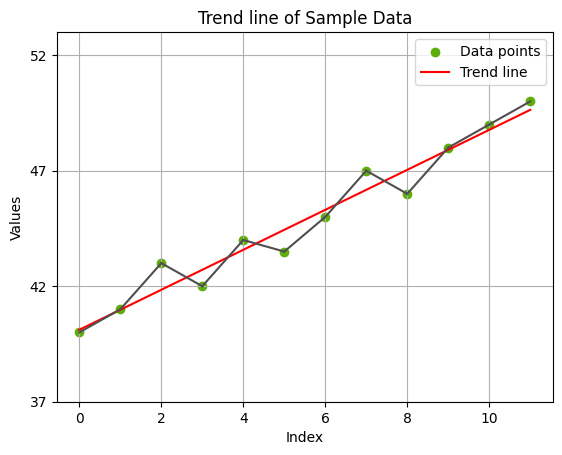
אבל למה לעצור כאן, בוא נחזק את הרושם על ידי כך שנעביר קו אופקי לרוחבו של הגרף עבור כל נקודה על ציר ה-y במקום עבור כל נקודה חמישית:

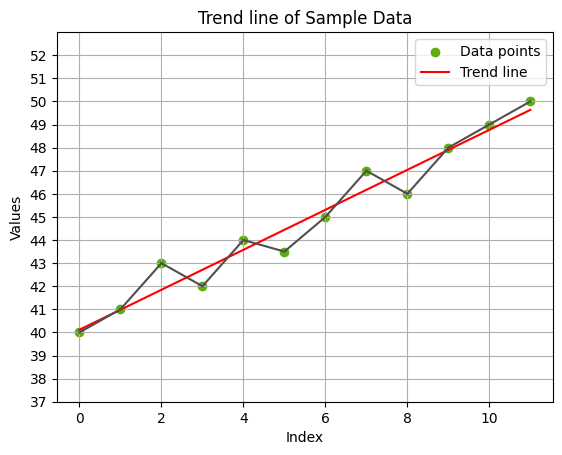
ככה הגרף נראה הרבה יותר טוב לדעתך, בפרט אם המסר שאתה רוצה להעביר הוא שהגודל אותו אתה מתאר צומח בקצב מהיר. אבל אם מצד שני אתה רוצה להמעיט במידת הגידול, מסיבותיך שלך, אתה תמיד יכול לחזור לגרסה המקורית.

זה בסה"כ גרף פשוט המראה כמה ניתן לשחק עם הצגת הנתונים ולנצל כשלים בתפיסה האנושית כדי לשכנע במה שבעל עניין מעוניין לתקשר. גרפים מתוחכמים יותר יכולים לעולל תעלולים מנטליים חמורים בהרבה. המתבונן הביקורתי חייב תמיד לעמוד על המשמר.

כשל התובע

שוד התרחש בעיירה המונה 10,000 תושבים. ראיות מהזירה גילו שמבצע העבירה נושא את הגן הנדיר A. גן שלפי ההערכות, מצוי ב-1% מהאוכלוסייה בלבד. חשוד נעצר בשכונה, ובדיקה מעבדתית זיהתה אותו כנשא של הגן הנדיר. בהתבסס על מידע זה, התובע טוען בבית המשפט שהחשוד הוא העבריין מעל לכל ספק סביר.

הבעיה בטענה של התובע היא שבעיירה קטנה של 10,000 תושבים עם שכיחות של 1%, בערך 100 תושבים עשויים לשאת את אותו הגן. על אחת כמה וכמה, אין כל ביטחון שהעבריין לא הגיע מחוץ לעיר.

כשל התובע הוא פגם בהיגיון הנובע מפירוש שגוי של הסתברות מותנית. הכשל הזה נפוץ במיוחד בהקשרים משפטיים, ומכאן נובע שמו.

הסתברות מותנית היא ההסתברות שמאורע אחד יתרחש בהינתן שכבר ידוע שמאורע אחר התרחש. ההסתברות מסומנת כ- P(A|B) ונקראת "ההסתברות של A בהינתן B".

כך זה פועל אצלנו:

• אירוע A: הגן A נמצא בזירת הפשע.
• אירוע B: הגן הנדיר מופיע רק באחוז קטן מהאוכלוסייה (1% במקרה שלנו).
• ההסתברות המותנית: P(A|B) היא ההסתברות למציאת הגן בזירה בהתחשב בשכיחות הנמוכה בה הוא מופיע באוכלוסייה.

מקור הטעות בהיפוך ההסתברות המותנית מ- P(A|B) ל- P(B|A) מה שגרם לתובע לטעון ששכיחותו הנמוכה של הגן (B), לצד זיהויו אצל הנאשם מוכיחה את היות החשוד בזירת הפשע (A).

ההיפוך של ההסתברות המותנית מוביל למסקנות שגויות. והראייה, במקרה שלנו, היא שאפילו בעיירה קטנה בת 10,000 תושבים ייתכנו 100 תושבים שנושאים את אותו הגן הנדיר ששכיחותו 1% בלבד. ואז הנאשם הוא 1 מ-100 מה שאומר שהסיכוי שהוא האשם, בהתבסס על ראייה זו בלבד, הוא 1% בלבד. מה שאומר שהנאשם הינו חף מפשע בהעדר ראיות מספיקות.

לסיכום, כשל התובע הופך את ההסתברות המותנה, ומסיק מסקנות שגויות. כי גם אם תכונה היא נדירה, באוכלוסייה גדולה מספיק ייתכנו מקרים נוספים שגם להם יש את אותה התכונה.

סיפורה המטריד של סאלי קלארק

בשנת 1996, בנם הראשון של סאלי ודונלד קלארק מת בגיל 11 שבועות בנסיבות שנראו כמו מוות בעריסה. שנה לאחר מכן, בנם השני מת בגיל 8 שבועות. בשלב זה, רשויות התביעה בבריטניה גיבשו תביעה נגד האם בחשד לרצח שני ילדיה.

במשפט העיד רופא נודע ומוערך שחישב ומצא כי הסיכוי של תינוק אחד למות מאותה התסמונת הוא 1 ל-8,543, ולפיכך הסיכוי למות שני התינוקות הוא ממש זעיר, רק 1 ל-73 מיליון (תוצאה של הכפלת ההסתברות בעצמה). מכיוון שהסיכוי לטרגדיה שכזו הוא כה נמוך, הרשיע חבר המושבעים את קלארק ברצח כפול ונגזרו עליה שני מאסרי עולם.

בשלב זה, סטטיסטיקאים מקצועיים בדקו את החישובים שהובילו להרשעה וגילו פגם מהותי בעדות הרופא. ההיגיון שבהכפלת הסיכויים של שני אירועים כדי להסיק את ההסתברות המשותפת שלהם מותנה בכך שהאירועים הם בלתי תלויים. במקרה זה, מכיוון ששני התינוקות היו אחים, אי אפשר לטעון שאין ביניהם תלות, במיוחד אם לוקחים בחשבון את האפשרות ששניהם נשאו את אותה מחלה גנטית.

מצוידים בהבנה זו ובבדיקות מעבדה שהראו כי הילדים מתו מסיבות טבעיות, הצליחו בעלה של סאלי וצוות ההגנה לזכות ולשחרר אותה מהכלא לאחר שלוש שנים בהן ריצתה מאסר על פשע שלא ביצעה. בעקבות הטרגדיה הדרדר מצבה הנפשי, וכעבור שנים מספר היא נמצאה בביתה ללא רוח חיים לאחר שמתה מהרעלת אלכוהול.

המסקנה שיכולה לחרוץ גורלות היא שלפני שכופלים הסתברויות של אירועים כדי לחשב את הסתברותם המשותפת צריך לוודא שהאירועים הם בלתי תלויים.

מתאם הוא לא סיבתיות

הניסיון הפרטי שלנו מלמד שככל שאנחנו נושפים יותר חזק על שבשבת רוח כך היא מסתובבת יותר מהר. התנסויות מסוג זה מלמדות אותנו שאם שני דברים קורים בסמיכות אז צריך להיות ביניהם קשר סיבתי.

באותה נשימה, מחקרים מצאו שילדים שצופים בתכנים אלימים בטלוויזיה נוטים להיות אלימים יותר.

האם המסקנה היא שהצפייה עצמה היא הגורם לאלימות? יכול להיות.

זו דוגמה למתאם (קורלציה) אשר קיים במציאות, ולמוח שלנו שממהר לקשר בין הדברים בקשר סיבתי כל שהוא. במקרה זה, התנהגות אלימה בילדים וצפייה בתכנים אלימים.

העניין הוא שבניגוד למקרה הנשיפה על השבשבת ברוב המתאמים בהם אנו נתקלים בחיי היום יום הסיבה והמסובב אינם כל כך קלים לפענוח. בדוגמה של הילדים שצופים בתכנים אלימים יכול להיות שילדים מחקים את ההתנהגויות שהם רואים בטלוויזיה אבל הסבר לא פחות משכנע הוא שילדים אלימים נמשכים מראש למראות אלימים.

הסיבה הגורמת לאנשים לייחס סיבתיות הכרחית למתאמים היא הנטייה האנושית לחשוב שאם שני דברים קורים בסמיכות אז אחד גורם לשני אבל זה לא תמיד המצב.

העובדה שיש מתאם בין שני דברים לא אומרת הרבה על הסיבה, אלא בעיקר ששני משתנים נוטים להשתנות יחדיו. לדוגמה, ישנו מתאם בין כמות הגלידה הנצרכת בק"ג לבין שיעור מכות השמש. האם הסיבה למכות השמש היא אכילת גלידה? או דווקא מכות שמש הם אשר גורמות לצריכה מופרזת של גלידה? ודאי שלא. הסיבה לעלייה בשכיחות מכות השמש היא השמש הקופחת של הקיץ שזו גם העונה שבה אנשים אוהבים לזלול גלידות. זו דוגמה למצב עניינים בו אין קשר סיבתי בין תופעות שיש ביניהם מתאם גבוה, כאשר הסיבה למתאם הינה גורם משותף המשפיע על שתיהן.

הדברים מגיעים לכדי אבסורד בעידן המידע בו ממש קל למצוא קורלציות. כל מה שצריך הוא להכניס המון נתונים למחשב ולבקש ממנו לפלוט צמדים שנראים מתואמים. לדוגמה, spurious correlations הכניס 25,237 משתנים למחשב שערך לא פחות מ- 636,906,169 השוואות ומצא אלפי מתאמים בין נתונים שמאוד קשה ואף בלתי אפשרי להסביר. בשיטה זו נמצאה קורלציה בין שיעור הגירושים במדינת מיין וצריכת המרגרינה כמו גם בין מספר התקפות שודדי הים למספר החיפושים בגוגל של "download firefox". בשכונה שבה גדלתי היו אומרים על זה "מה קשור?"

המסקנה היא שאין למהר ולקפוץ למסקנות בדבר קשר סיבתי בין שני גורמים רק על בסיס העובדה שהם מתרחשים בסמיכות או משתנים יחדיו.

הנאחס שמביאים עיתוני הספורט ותסוגה לממוצע

אחד המגזינים היוקרתיים בעולם הספורט במשך 70 השנים האחרונות הוא Sports Illustrated, מה שאמור להפוך את ההופעה על שער המגזין לנחשקת עבור ספורטאים וקבוצות מקצועיות. אלא שבפועל, קיים דפוס שבו ספורטאים וקבוצות המופיעים על שער המגזין נוטים להידרדר בביצועיהם לאחר הפרסום. אגדה אורבנית מייחסת זאת ל"נאחס" (במקור: jinx) שמביא הפרסום על השער.

אבל כאשר בוחנים את התופעה לעומק, מתגלה הסבר אחר, מבוסס יותר. הסיבה נעוצה בעובדה שההופעה על שער המגזין נובעת לרוב מהישג יוצא דופן – הישג שקשה מאוד לשחזר. הקושי לשחזר ביצועים גבוהים קשור לתופעה סטטיסטית רחבה יותר שנקראת רגרסיה (תסוגה) לממוצע.

מהי רגרסיה לממוצע?

רגרסיה לממוצע מתארת מצב שבו תוצאה קיצונית (גבוהה או נמוכה) בדגימה אחת נוטה להתקרב לממוצע בדגימות הבאות. התופעה זוהתה לראשונה במאה ה-19 על ידי המדען הבריטי סר פרנסיס גלטון. במחקריו גילה גלטון שילדים להורים גבוהים מאוד נוטים להיות גבוהים מהממוצע – אך עדיין נמוכים מהוריהם.

האם שבחים או גערות מועילים יותר כשמדריכים את חניכי קורס הטיס של חיל האוויר?

חתן פרס נובל, דניאל כהנמן, משתף בספרו "לחשוב מהר ולאט" אירוע המדגים היטב את כוחו של עיקרון זה. בשיחה שקיים עם מדריכי טיסה של חיל האוויר, הוא ציין שמחקרים פסיכולוגיים מראים כי שבחים מועילים יותר מגערות.

בתגובה, אחד המדריכים ביקש את רשות הדיבור ואמר: "מניסיוני, המצב הפוך לחלוטין. בכל פעם ששיבחתי חניכים על ביצועים טובים, הם נחלשו בהמשך. מנגד, כשגערתי בהם על טעויותיהם, הם נטו להשתפר."

כהנמן מתאר כיצד באותו רגע חווה הארה. הוא הבין שהתופעה שתיאר המדריך אינה נובעת מכוחם של שבחים או גערות, אלא מתסוגה לממוצע: חניכים שהצליחו באופן יוצא דופן בביצוע אחד, נטו להצליח פחות בביצוע הבא – ללא קשר לתגובה שקיבלו מהמדריך. באותו אופן, חניכים שביצועיהם היו גרועים במיוחד, נטו להשתפר בביצוע הבא.

כדי להדגים זאת, כהנמן ביקש מהמדריכים לנסות לקלוע מטבע למטרה מאחורי ראשם, בלי להסתכל. תוצאות הניסוי הראו:

• משתתפים שקלעו רחוק מהמטרה בביצוע הראשון, נטו להשתפר בביצוע הבא.
• לעומתם, משתתפים שהיו קרובים מאוד למטרה בביצוע הראשון, נטו להתרחק ממנה בביצוע הבא.

והכל – ללא קשר לגערות או שבחים שקיבלו.

לסיכום, תופעת הרגרסיה לממוצע מזכירה לנו שתוצאות קיצוניות הן לעיתים קרובות תולדה של מזל או תנאים חד-פעמיים, וכי בחיים (ובסטטיסטיקה) יש נטייה טבעית להסתדר סביב הממוצע.

פרדוקס סימפסון

נבחן דוגמה פשוטה המתארת את השפעת הטיפול במחלה על שתי קבוצות – בני אדם ועכברים. הטבלה הבאה מציגה את שיעורי ההחלמה בכל קבוצה:

במעבר לאחוזים:

נסכם את הטבלה במילים:

אצל העכברים 100% החלימו לאחר שקיבלו טיפול ורק 75% מבין אילו שלא קיבלו טיפול.

אצל בני האדם 25% החלימו לאחר שקיבלו טיפול ו-0% החלימו מבין אילו שלא טופלו.

המסקנה כאן נראית ברורה – הטיפול משפר את סיכויי ההחלמה.

אבל אם מסתכלים על סך כל המחלימים משתי הקבוצות יחדיו:

• סך המחלימים בקרב המטופלים: 20 מתוך 50 (40%).
• סך המחלימים בקרב הלא-מטופלים: 30 מתוך 50 (60%).

ולכן, המסקנה היא הפוכה שהטיפול דווקא מפחית את אחוזי ההחלמה.

זו דוגמה לפרדוקס סימפסון. תופעה בה מגמה מסוימת נצפית בכמה קבוצות נתונים אך נעלמת או אפילו מתהפכת כאשר מאחדים את הקבוצות.

מקור הבעיה במשתנים מתערבים שלא נותנים עליהם את הדעת. בדוגמה שלנו, ייתכן שמראש נותנים את הטיפול לאנשים שמצבם חמור יותר ולכן סיכויי ההחלמה של אנשים שהשתתפו בניסוי הם מראש פחותים. משתנה זה (חומרת המחלה) הוא קריטי, וההתעלמות ממנו עלולה להוביל למסקנות שגויות.

הלקח הוא שכאשר בוחנים נתונים סטטיסטיים, צריך לקחת בחשבון שדרך חלוקת המידע יכולה ואף עלולה להשפיע על התוצאות.

פרדוקס ברקסון: הטיית בחירה במסווה של קשר סטטיסטי

דמיין חוקר הבוחן את הקשר בין מהירות הקלדה ליכולת שכנוע בקרב מועמדים לעבודה. במחקרו, הוא מוצא קורלציה שלילית בין שני המשתנים באוכלוסייה הנבדקת.

עם זאת, מבט רחב יותר על כלל האוכלוסייה מגלה כי למעשה אין כל קשר בין המשתנים הללו.

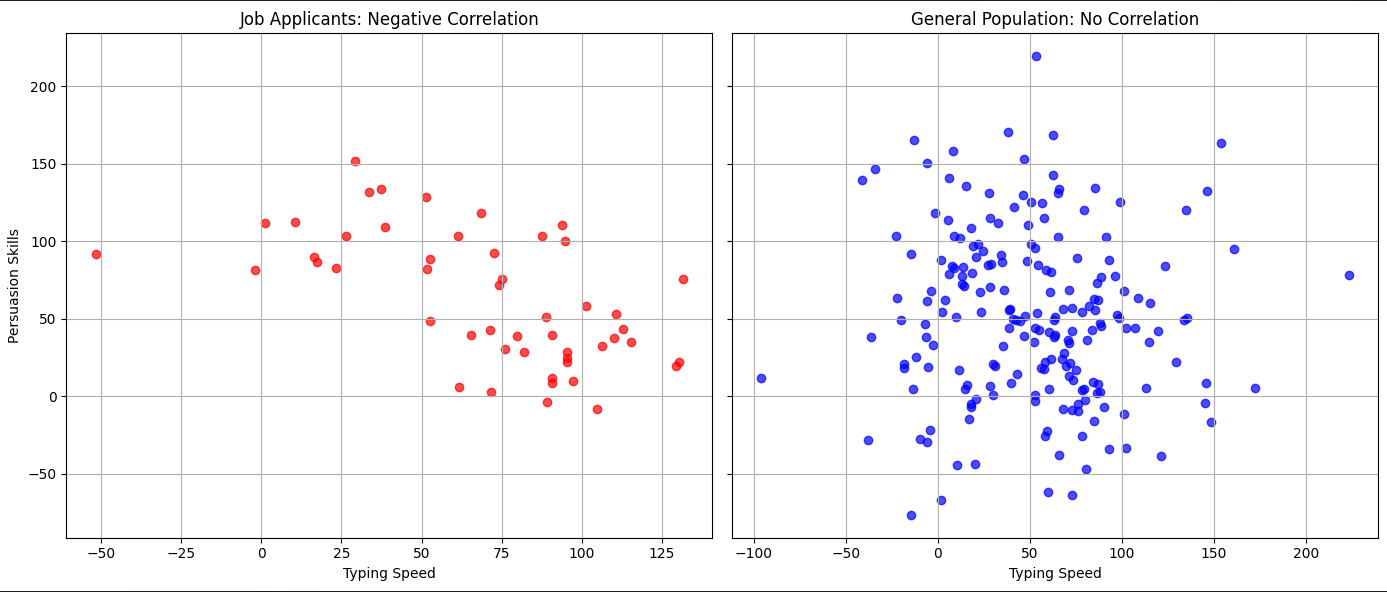
איך נוצר הפער בין ממצאי המחקר למציאות? התשובה טמונה בפרדוקס ברקסון (Berkson's Paradox) – תוצאה של הטיית בחירה. כאשר האוכלוסייה הנבדקת אינה מייצגת נאמנה את כלל האוכלוסייה, עשוי להיווצר קשר סטטיסטי מלאכותי בין שני משתנים שאינם תלויים זה בזה באמת.

במקרה זה, ייתכן שמועמדים לעבודה נבחרו מראש לפי יכולת יוצאת דופן באחד משני התחומים: מי שמצטיינים בשכנוע אך מקלידים לאט, ומי שמקלידים במהירות אך פחות משכנעים. תהליך הבחירה עצמו יוצר את הקורלציה השלילית, אף שהיא אינה קיימת באוכלוסייה הרחבה.

פרדוקס או הטייה?

חשוב להבין כי פרדוקס ברקסון אינו "פרדוקס" במובן המתמטי, אלא תופעה הנובעת מאיסוף נתונים לא מייצג. הוא מדגים בעיה רחבה יותר של הטיית בחירה – בחירת תת-אוכלוסייה בעלת מאפיינים ייחודיים (לעתים שלא מדעת), דבר המשפיע על הקשרים הסטטיסטיים הנמדדים.

דוגמה נוספת: טעויות בסקרים פוליטיים

הטיית בחירה דומה עשויה להסביר מדוע סוקרים נוטים לפספס את תוצאות הבחירות. לדוגמה, במקרים בהם סקרים מצביעים על יתרון למועמדים ליברליים, אך התוצאות בפועל נוטות לכיוון השמרני. אחת הסיבות לכך היא שהאוכלוסייה המוכנה להשתתף בסקרים עשויה להיות בעלת נטיות ליברליות יותר, מה שגורם לתמונה שאינה מייצגת את כלל ציבור הבוחרים.

כיצד ניתן להתמודד עם הטיית ברקסון?

הטיית ברקסון נובעת מהגדרת אוכלוסייה שאינה מייצגת את כלל האוכלוסייה. הפתרון הפשוט ביותר הוא להימנע ככל האפשר מהתניות המגבילות את האוכלוסייה הנדגמת. במקרים שבהם הגבלות הן בלתי נמנעות (למשל, כאשר נבחנת תת-קבוצה מוגדרת), יש להצהיר על כך בגלוי בחלק השיטות והמסקנות, ולציין שהממצאים תקפים רק לאוכלוסייה מסוימת.

פרדוקס ברקסון מול פרדוקס סימפסון

בעוד פרדוקס סימפסון נובע מהתעלמות מגורם מתערב, פרדוקס ברקסון נוצר מהכנסת תנאי שאינו הכרחי. בהתאם, הפתרון לסימפסון הוא תיקון באמצעות התחשבות בגורם המתערב, ואילו הפתרון לברקסון הוא הימנעות מתנאים המגבילים את האוכלוסייה המשתתפת במחקר.

לסיכום

כצרכן נתונים שלא רוצה ליפול בפח, חיוני שתפתח חשיבה ביקורתית ותחקור את המידע אליו אתה נחשף. חפש מקורות המספקים מבט מקיף ומאוזן של הנתונים, כולל ראיות התומכות וסותרות את דעתך. נסה לתפוס את מה שחסר. היזהר מפני סטטיסטיקות או אנקדוטות שנבחרו בקפידה ומציגות תמונה מגמתית. השתדל לבדוק את השיטה בה נאספו ונותחו הנתונים, ונסה להבין עד כמה היא ניטרלית ויסודית. הכר בכך שמידע אינו צף בחלל ריק, כי כל מידע שאתה נעשה מודע לו אינו אלא פיסה בתצרף גדול יותר, ונסה להבחין כיצד כל פרט מידע משתלב בתמונה הרחבה. על ידי עמידה על המשמר והפעלת שיקול דעת וביקורתיות, תוכל להגן על עצמך מפני נפילה בפח של מסקנות שגויות מצידם של חוקרים גרועים או טקטיקות הטעיה בהם נוקטים בעלי עניין שעלולים לפגוע בך אם רק תיתן להם.

רשימה לא ממצה של מקורות מידע

בכתיבת המדריך נעזרתי, בין השאר, במקורות הבאים:

• How to lie with statistics/Darrell Huff ספר קצר זה נכתב ב-1954 ועדיין מצליח לספק מבוא מאיר עיניים ומשעשע לדרך שבה מפרסמים מתוחכמים מצליחים לבלבל אותנו עם מספרים. באופן אישי, כל כך הושפעתי ממנו בשלב מסויים עד שעשיתי כל שיכולתי כדי להתחמק מעבודה הדורשות ניתוח סטטיסטי. מאז התבגרתי, וחזרתי לעבוד עם סטטיסטיקה בתור כלי עזר חשוב תוך שאני מקפיד על הלך רוח ספקני לגבי התוצאות שאני מפיק כמו גם לגבי תוצאות של אחרים. באופן רחב יותר, אני מאמין שצריכת ידע תוך גילוי ספקנות בריאה הינה הדרך הטובה ביותר לנסות ולהבין את טבעו של העולם.
• ויקיפדיה האנגלית היא כמעט תמיד מקור נפלא להרחבת הדעת. לצורך הכנת המדריך נעזרתי בערכים המצוינים המטפלים בSimpson's paradox ובBerkson's pardox.
• על התהליך הרשלני שגרם להטעיית הקהילה המדעית בכל הנוגע לנזקי הסוכר ניתן לקרוא במאמר הבא.
• ספרו של חיים שפירא "תנינים, הימורים וימי הולדת" הוא אולי המעמיק ביותר שקראתי שעדיין מתאים לקהל הרחב. הכותב המיומן מסכם את הניסיון שצבר מעשרות שנים בתור מרצה לסטטיסטיקה במוסדות להשכלה גבוהה. בין שלל הנושאים בספר נמצא גם הסבר מקיף יותר על כשל התובע, ההבדל שבין מתאם וסיבתיות ופרדוקס סימפסון.

אולי גם זה יעניין אותך

חוק בייס (bayes) והבנת המציאות

רשימה לא ממצה של שגיאות לוגיות

10 הטיות קוגניטיביות שאתה חייב להכיר

כישורי חיים - רעיונות ששווה לשתף

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים