חיזוי מחירי בתים באמצעות למידת מכונה ומודל מרובה משתנים
פורסם במקור:
תאריך עדכון אחרון:
אחרי שבמדריך הקודם פיתחנו מודל רגרסיה קווית באמצעות TensorFlow על משתנה אחד בלבד (חיזוי מחירי דירות בהינתן השטח) במדריך הנוכחי נמשיך באותו נושא ונלמד את המכונה לחזות את מחירי הדירות על סמך מספר משתנים (שטח דירה, מספר חדרי השינה ומספר חדרי שירותים). חיזוי על סמך מספר משתנים מכונה ניתוח רב משתנים (multivariate analysis).
המשתנים במדריך שישמשו לאנליזה מתחלקים לשניים, מספריים וקטגוריים. המטרה שלנו היא לפתח מודל שלתוכו נזין את הנתונים של הדירה. שטח, מספר חדרי השינה, סוג הדירה (מגורים, פרטית או רב-משפחתית) ונקבל הערכה של שווי הנכס.
לצורך פיתוח המודל נשתמש ב-TensorFlow 2 שהיא ספרייה של למידת מכונה שפותחה על ידי גוגל, ומשמשת, בין השאר, את מנוע החיפוש הטוב ביותר באינטרנט.
לחץ כאן כדי להוריד קובץ csv של מסד הנתונים
להורדת המחברת אותה נפתח במדריך
* המדריך הנוכחי מבוסס על מדריך קודם מודל רגרסיה לינארית באמצעות TensorFlow 2 על משתנה אחד בלבד שבו הסברתי כיצד לבנות מודל של למידת מכונה. אם לא קראתם את המדריך הקודם ואין לכם מספיק ידע בתחום, רצוי שתתחילו מקריאת המדריך הקודם שמניח את היסודות לנוכחי.
ייבוא תלויות וספריות
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt- ספריית Numpy מאפשרת לעבוד עם מערכים רב-ממדיים, ומספקת פונקציות לביצוע פעולות של אלגברה לינארית הנדרשות לפתרון הבעיות המתמטיות בתהליך הלמידה.
- Pandas משמשת לסידור ולסינון מידע בדומה לגיליון אקסל.
- Matplotlib משמשת להצגת מידע באמצעות גרפים ותרשימים.
TensorFlow 2 היא הספרייה בה נשתמש ללמידת מכונה. אני משתמש בגרסה 2.5 מכיוון שהיא העדכנית ביותר בזמן עריכת המדריך.
נתקין את הגרסה שמעניינת אותנו:
!pip install tensorflow==2.5.0את המדריך פתחתי בסביבת Colab ומשמעות סימן הקריאה (!) בתחילת השורה הוא שימוש בטרמינל המובנה של סביבת הפיתוח.
נייבא:
import tensorflow as tfנוודא שייבאנו את הגרסה שבה אנו מעוניינים:
print(tf.__version__)2.5.0
ייבוא מסד הנתונים
מסד הנתונים המשמש במדריך מסכם את מחירם של בתים שנמכרו בסקרמנטו. תוכלו להוריד אותו מכאן.
df = pd.read_csv('./sacramentorealestatetransactions.csv',usecols=['beds','baths','sq__ft','type','price'])
סקירת הנתונים וניקוי דוגמאות חריגות
קודם כל, נסקור את מסד הנתונים כדי לנסות לחוש אותו ולנקות ממנו דוגמאות חריגות.
df.shape(985, 5)
- חמישה טורים ו-985 שורות.
מה סוג הנתונים?
df.info()RangeIndex: 985 entries, 0 to 984 Data columns (total 5 columns): beds 985 non-null int64 baths 985 non-null int64 sq__ft 985 non-null int64 type 985 non-null object price 985 non-null int64 dtypes: int64(4), object(1) memory usage: 38.6+ KB
- כל הטורים מספריים מלבד type שהוא שמי וקטגורי.
האם חסרים נתונים?
df.isna().sum()beds 0 baths 0 sq__ft 0 type 0 price 0 dtype: int64
- לא.
כיצד מתפלג סוג הדירות?
df.type.value_counts()Residential 917 Condo 54 Multi-Family 13 Unkown 1 Name: type, dtype: int64
- הנתונים לא מאוזנים כאשר 93% מהמגורים שייך לסוג Residential.
מהי התפלגות הנתונים המספריים?
# plot histograms for each cols
for i, col in enumerate(['beds', 'baths', 'sq__ft', 'price']):
plt.subplot(1, 4, i+1)
df[col].plot(kind='hist', title=col)
plt.xlabel(col)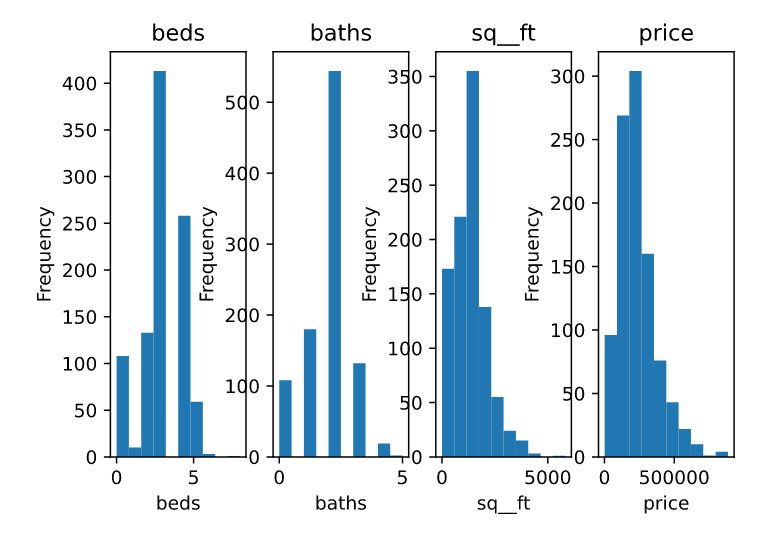
- בעוד הערכים עבור מיטות וחדרי שירותים מראים התפלגות נורמלית מחיר הדירות וגודלם נוטה לעבר הערכים בצד הנמוך של ההתפלגות.
- עמודות שונות מבוטאות בסדרי גודל שונים. לדוגמה: חדרים באחדות לעומת מחיר בדולרים ששואף למיליון. כדי להקל על התכנסות המודל נצטרך לנרמל את הנתונים.
מהם הערכים הסטטיסטיים של המשתנים המספריים?
df.describe()| beds | baths | sq__ft | price | |
|---|---|---|---|---|
| count | 985.000000 | 985.000000 | 985.000000 | 985.000000 |
| mean | 2.911675 | 1.776650 | 1314.916751 | 234144.263959 |
| std | 1.307932 | 0.895371 | 853.048243 | 138365.839085 |
| min | 0.000000 | 0.000000 | 0.000000 | 1551.000000 |
| 25% | 2.000000 | 1.000000 | 952.000000 | 145000.000000 |
| 50% | 3.000000 | 2.000000 | 1304.000000 | 213750.000000 |
| 75% | 4.000000 | 2.000000 | 1718.000000 | 300000.000000 |
| max | 8.000000 | 5.000000 | 5822.000000 | 884790.000000 |
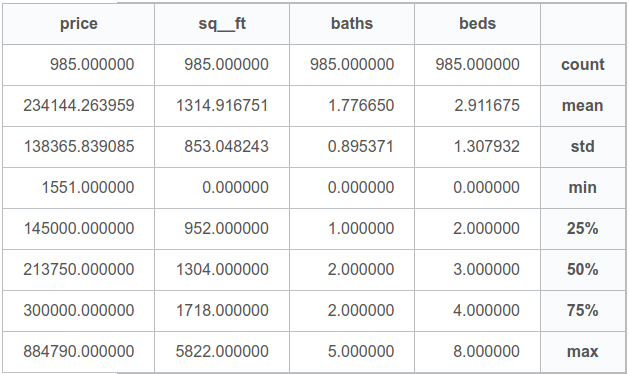
- לפי ערכי המינימום, אפשר לראות שחלק מהעמודות כוללות ערכי 0. לדוגמה, מספר חדרים אפסי או שטח אפסי. זה עלול לפגוע בתוצאות האנליזה.
ננקה את הנתונים.
ניקוי המידע
ננקה את מסד הנתונים שלנו מכל הדוגמאות שבהם השטח נמוך מ-10 וגם מדוגמאות שבהם מספר חדרי השינה או השירותים אפסי.
filtered_data = df[(df.sq__ft > 10) & (df.beds > 0) & (df.baths > 0)]- השם של מסד הנתונים אחרי הניקוי הוא filtered_data. את מסד הנתונים המקורי df נשים בצד. אולי נצטרך אותו בהמשך.
מעניין מה מידת הקורלציה בין שטח הבית לבין יתר המשתנים.
filtered_data.corr()['sq__ft'].sort_values()price 0.693708 beds 0.695710 baths 0.724631 sq__ft 1.000000 Name: sq__ft, dtype: float64
.שטח הבית נמצא בקורלציה חיובית וחזקה למדי עם המחיר וגם עם מספר החדרים
האם ניתן לאתר דוגמאות חריגות נוספות?
def plot_ft_vs_price():
plt.plot(filtered_data['sq__ft'], filtered_data['price'], 'o')
plt.ylabel('Price')
plt.xlabel('Square foot')
plt.title('Price vs square foot')
plot_ft_vs_price()אפשר לראות דוגמה חריגה כאשר השטח גדול מ-5000. נסיר גם את הדוגמה הזו.
filtered_data = filtered_data[(filtered_data.sq__ft < 5000)]
קידוד המשתנים הקטגוריים
שימוש במשתנה קטגורי (שמי) מציב בעיה מפני שמחשבים צריכים מספרים כדי לעבוד איתם. גישה אחת לפתרון הבעיה היא למפות כל אחת מהקטגוריות למספר. הבעיה עם הגישה הזו שמודלים של למידת מכונה מניחים שיש למספרים ערך כמותי. לדוגמה, אם אנחנו נקודד את השכונות למספרים. שכונה א תקבל את הערך 1, שכונה ב את הערך 2 ושכונה ג את הערך 3. המודל עלול להסיק ששכונה א + ב שוות לשכונה ג. כדי למנוע את הבעיה משתמשים בקידוד one hot encoding שהופכת את המשתנה השמי למערך של 0 ו-1 שבו כל המשתנים מקבלים 0 לבד מאחד שמקבל 1. כל קטגוריה מקבלת 1 במקום שונה במערך.
בוא נראה איך עושים את זה, ובסוף הדוגמה תוכלו לראות בעצמכם איך נראים משתנים קטגוריים אחרי קידוד בשיטת one hot encoding.
נעזר ב-numpy כדי למצות את שמות הקטגוריות של סוגי הדירות.
type_names = np.unique(np.array(filtered_data.type))
type_namesarray(['Condo', 'Multi-Family', 'Residential'], dtype=object)
3 שמות ל-3 סוגים.
נשתמש ב-pandas כדי לקודד בשיטת one-hot encoding, המתאימה לקידוד נתונים קטגוריים.
t_dummies = pd.get_dummies(filtered_data.type, dummy_na=False)נציץ במספר דוגמאות אקראיות כדי לראות את הקידוד בפעולה:
t_dummies.tail(3)| Condo | Multi-Family | Residential | |
|---|---|---|---|
| 979 | 0 | 0 | 1 |
| 297 | 0 | 0 | 1 |
| 344 | 1 | 0 | 0 |
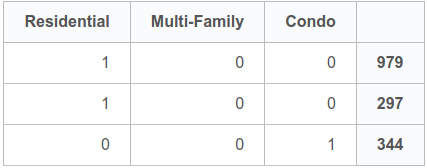
- דוגמאות 979 ו-297 שייכות לקטגוריה Residential
- דוגמה 344 שייכת לקטגוריה Condo.
נסיר את העמודה type כי קודדנו אותה באמצעות one-hot encoding ואנחנו לא מעוניינים שעמודה שמית תפריע למודל שלנו שיודע לעבוד עם נתונים מספריים בלבד.
type = filtered_data.pop('type')נאחד את כל העמודות למסד נתונים אחד שנקרא לו merged.
merged = pd.concat([filtered_data, t_dummies], axis=1)נציץ בזנבו של מסד הנתונים המאוחד כדי לוודא שהאיחוד בין העמודות נעשה כהלכה. אם האינדקסים אינם מתואמים בין העמודות השונות נראה ערכים חסרים בזנב.
merged.tail(3)| beds | baths | sq__ft | price | Condo | Multi-Family | Residential | |
|---|---|---|---|---|---|---|---|
| 982 | 3 | 2 | 1216 | 235000 | 0 | 0 | 1 |
| 983 | 4 | 2 | 1685 | 235301 | 0 | 0 | 1 |
| 984 | 3 | 2 | 1362 | 235738 | 0 | 0 | 1 |
- אין נקודות מידע חסרות. נראה שתהליך האיחוד עבר בשלום.
נורמליזציה
עדיין יש לנו בעיה אחת משמעותית והיא שהנתונים שלנו אינם על אותה הסקלה כי השטח נמדד ביחידות של עשרות ואף מאות בעוד החדרים נמדדים ביחידות בודדות. כדי לפתור את הבעיה ננרמל את הנתונים כך שכל אחד מהפיצ'רים יהיה בדיוק באותה הסקלה עם ממוצע 0 וסטיית תקן 1.
* את המשתנה הקטגורי type שעשינו לו one-hot encoding לא צריך לנרמל כי הערכים שבו הם בין 0 ל-1 כך שהם מתאימים מראש לסקלה המנורמלת.
את הערכים המנורמלים נאסוף לתוך DataFrame שאותו נכנה בשם normalized.
normalized = pd.DataFrame()
for col in merged.columns:
if col in ['Condo', 'Multi-Family', 'Residential']:
normalized[col] = merged[col]
else:
normalized[col] = normalize(merged[col])איך נראים הנתונים המנורמלים?
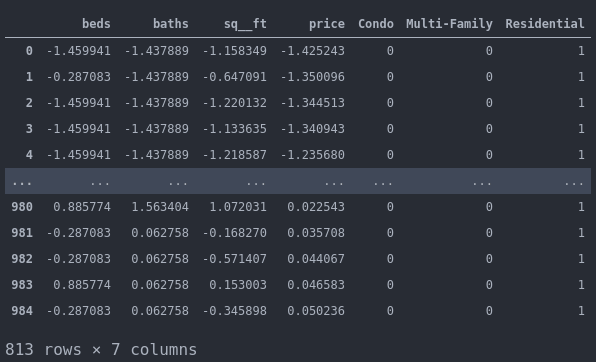
מהם הערכים הסטטיסטיים המאפיינים את הנתונים המנורמלים?
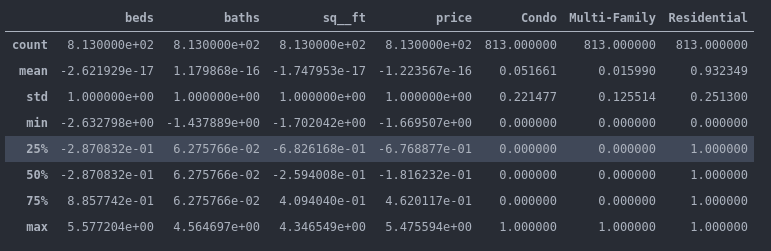
- העמודות אותם נרמלנו מתאפיינות בממוצע 0 וסטיית תקן 1.
המודל צריך לחזות את המחיר המנורמל:
y = filtered_data.pop('price')
היתר מהווים את המשתנה הבלתי תלוי:
X = normalized.drop(['price', 'Condo'],axis=1)
הסרתי את המשתנה Condo כדי להמנע מסכנת collinearity תופעה שבה המשתנה נמצא בקשר ליניארי הדוק עם משתנים אחרים ולכן אין בו צורך בשביל התחזית. במקרה שלנו, אם הסוג הוא לא Residential וגם לא Multi-Family אז הוא בהכרח Condo.
הפרדת הנתונים לסט אימון ומבחן
נפריד את מסד הנתונים לשני מסדים - אימון ומבחן:
# Split the data to test and train groups
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.33, random_state=42)
אימון המודל
את המודל נפתח באמצעות TensorFlow 2.
נייבא את החבילות:
# Imports
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Activation
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.callbacks import EarlyStoppingנבנה את המודל:
model = Sequential()
# The model receives 5 inputs and outputs a single value
model.add(Dense(32, activation='relu', input_shape=(5,)))
model.add(Dense(32, activation='relu'))
model.add(Dense(1))- אנחנו מזינים את המודל ב-5 קלטים (שטח, מספר חדרים, מספר שירותים ושני סוגי דירות) ומצפים לקבל פלט יחיד (מחיר), וזה מה שמכתיב את הארכיטקטורה של המודל.
- השכבות הם צפופות dense, וכוללות 32 נוירונים בשתי השכבות הראשונות
- בין שכבת הקלט ושכבת הפלט ישנה שכבה חבויה אחת.
- פונקצית האקטיבציה היא relu שהיא הבחירה ברירת המחדל בעולם למידת המכונה.
נתאר את המודל:
model.summary()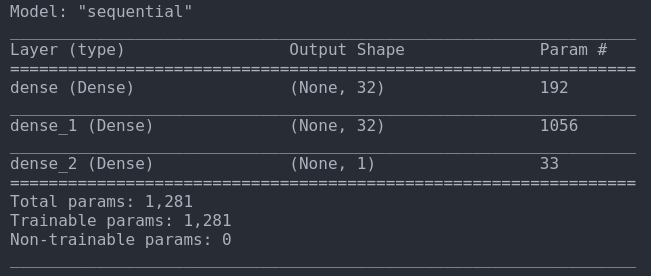
נקמפל את המודל:
# Compile the model
model.compile(Adam(), 'mean_squared_error')האופטימיזציה נעשית באמצעות ADAM.
הפונקציה EarlyStopping מפסיקה את תהליך הלמידה כאשר המודל מתכנס והתוצאות מתחילות להדרדר.
# The EarlyStopping callback stops the learning process
# if the loss doesn't improve
es = EarlyStopping(monitor='val_loss',
min_delta=0,
patience=10,
verbose=1,
mode='auto',
restore_best_weights=True)את הסבלנות patience קבעתי על 10 epochs שבמהלכם המודל ימשיך לבדוק האם הגיע לאופטימום . בכל מקרה, האלגוריתם יבחר את ה-epoch האופטימלי וממנו הוא ייקח את המשקלים.
נריץ את המודל:
model.fit(X_train,
y_train,
batch_size=32,
epochs=10000,
validation_data=(X_test,y_test),
callbacks=[es])תמונת האילוסטרציה הבאה מדגימה כיצד נראה תהליך האימון. במציאות, המודל רץ 17 epochs עד שפונקציה ה-EarlyStopping עצרה אותו.
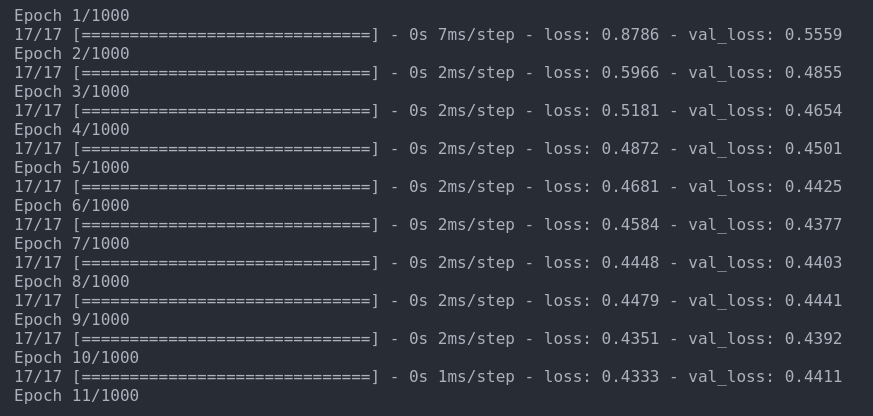
הערכת המודל
יש לנו מודל. קוראים לו model, אבל מה הוא אומר לנו על הנתונים? עד כמה הוא מצליח לתאר בצורה טובה את סט הנתונים? האם נצליח להפיק ממנו תחזיות מספקות לגבי סט נתוני המבחן?
לפני שנראה את התוצאות אני רוצה להזכיר שהמודל חוזה את שיעור סטיית התקן של המחיר ולא את המחיר עצמו.
קודם כל, כדי לקבל תחושה נחשב את המחיר הצפוי עבור דירה אחת מסוימת בסט נתוני המבחן. במקרה זה, בחרתי באקראי ברשומה 273.
סטיית התקן של מחיר הדירה על פי המידע שסיפק לנו מסד הנתונים היא 0.5205240105653677
מחיר הדירה על פי מסד הנתונים הוא 292000
הפונקציה הבאה תעזור לנו לחשב את סטיית התקן והממוצע עבור כל עמודה:
def get_col_stats(x):
return {"mean": x.mean(), "std": x.std()}במקרה של המחיר:
get_col_stats(merged.price){'mean': 229728.13407134073, 'std': 119633.03260693513}
המחיר בפועל הוא תוספת שיעור סטיית התקן לממוצע המחיר:
actual_value = mean + stdev * normalized_value
נעזר בזה כדי לחשב את המחיר:
calc_price = 229728 + 119633 * 0.5205240105653677התוצאה: 292000 הינה בהסכמה עם המידע במסד הנתונים.
כמה סטיות תקן חוזה המודל עבור הדוגמה?
y_pred = model.predict(X_test.loc[273].values.reshape(1, -1))
y_pred[0][0]0.8479233 סטיות תקן
- את הפונקציה predict צריך להזין במערך דו ממדי אבל כל רשומה היא מערך חד-ממדי אז כדי להוסיף את הממד החסר השתמשתי בפונקציה של Pandas reshape(1, -1)
- המודל חוזה את מספר סטיות התקן של התוצאה מהממוצע. נחלץ את הערך הזה: y_pred[0][0]
מה המחיר הצפוי?
calc_price = 229728 + 119633 * y_pred[0][0]331167
נסכם. הערך החזוי לעומת הערך בפועל:
Predicted value: 331167 Actual value: 291999
יכול להיות שהתוצאות בטווח השגיאה של המודל, אבל מהו טווח השגיאה של המודל? כדי למצוא אותו נעשה את התחזית על כל הדוגמאות.
y_pred = model.predict(X_test)נעריך את המודל:
from scipy import stats
slope, intercept, r_value, p_value, std_err = stats.linregress(y_test, y_pred.reshape(-1))
idx = ['slope', 'intercept', 'r_value', 'p_value', 'std_err']
data = np.array([slope, intercept, r_value, p_value, std_err])
print(pd.DataFrame(data = data, index = idx , columns = ['values']))slope 5.390084e-01 intercept 2.568196e-02 r_value 7.034193e-01 p_value 1.786228e-41 std_err 3.333173e-02
- המודל מנסה לשרטט קו ישר כדי לתאר את הנתונים.
- הנחת היסוד שלנו היא שהמודל לא מצליח לנבא את התוצאה. p_value נמוך מרמת סף (לדוגמה, נמוך מ-0.05) מחזק את הבטחון שלנו ביכולת הניבוי של המודל. הערך הגבוה ביותר הוא 1 והכי נמוך הוא 0. הערך המאוד נמוך שקבלנו מאפשר לנו להפריך את הנחת היסוד ולהסיק שהמודל מספק תוצאות בעלות משמעות סטטיסטית.
- standard error מעריך עד כמה הדוגמה שלקחנו בשביל המחקר מייצגת את האוכלוסיה. השגיאה הסטנדרטית לוקחת בחשבון את השונות ומספר הפריטים בדוגמה (ולא באוכלוסיה). מספר גבוה של דוגמאות ושונות נמוכה מוריד את המדד. הערך הנמוך שהפיק המודל מחזק את הבטחון שלנו במידה שהדוגמה מייצגת את האוכלוסיה.
נשרטט את ניבוי המודל כקו ישר על גבי הנתונים המקוריים. נתחיל ממשוואת הקו הישר והתחזיות שהיא מנפקת:
predict_line = lambda S: 5.390084e-01 * y_test + 2.568196e-02
# There exists only one straight line passing through two distinct points
two_pts_for_the_line = np.array([y_test.min(), y_test.max()])
predicted_line = predict_line(two_pts_for_the_line)נשרטט את הניבוי על גבי הנתונים:
plt.plot(y_test, y_pred, 'b+')
plt.plot(y_test, predicted_line, color='red')
plt.xlabel("Prices")
plt.ylabel("Predicted prices")
plt.title("Actual Vs. Predicted prices")
plt.tight_layout()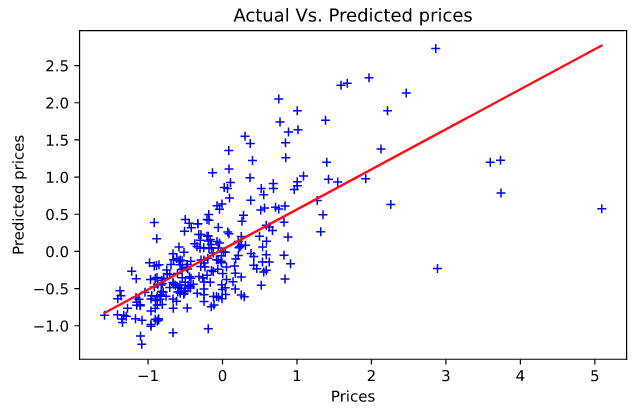
עד כמה התיאור שמנפק המודל נאמן למציאות? בשביל זה אנחנו צריכים מדדים סטטיסטיים נוספים.
from sklearn import metrics
print('MAE: %.2f' % metrics.mean_absolute_error(y_test, y_pred))
print('MSE: %.2f' % metrics.mean_squared_error(y_test, y_pred))
print('RMSE: %.2f' % np.sqrt(metrics.mean_squared_error(y_test, y_pred)))
print('R^2: %.3f' % r_value**2)MAE: 0.46 MSE: 0.45 RMSE: 0.67 R^2: 0.495
ככל שהערך של MAE נמוך יותר, כך המודל מדויק יותר.
מדד RMSE הוא היותר שימושי לנו מפני שהוא מבטא את טווח השגיאה באותם היחידות של הטור שאותו אנו מנסים לחזות. לפיכך, טווח השגיאה של המודל הוא +/- 0.67 סטיות תקן.
בהקשר של התוצאה שקיבלנו עבור דוגמה 273 ההפרש בין סטיית התקן שחזה המודל ובין הערך בפועל היא 0.32 ולכן התצפית היא בטווח.
R² הוא שיעור השונות בנתונים שהמודל מצליח להסביר. הערך הגבוה ביותר הוא 1. ערך 0 או נמוך יותר מעיד על מודל לא מוצלח. מערך R² של 0.5 אנחנו יכולים ללמוד שהמודל מצליח לחזות את התוצאות במידה בינונית בלבד.
שמירה
נשמור את המודל:
model.save('predict_house_prices.h5')
סיכום
במדריך הזה למדנו לפתח מודל של רגרסיה שתלוי במספר משתנים בלתי תלויים. למדנו לקודד משתנים קטגוריים בשיטת one-hot encoding, ולנרמל נתונים מספריים כדי למנוע את ההשפעה הלא רצויה של שיעור גודל שונה בין עמודות הנתונים על התכנסות המודל. כמו כן, פיתחנו מודל למידת מכונה עמוק שכולל שכבה חבויה אחת.
במדריך הבא נפרוס את המודל על שרת כדי שמשתמשים יוכלו להוציא תחזיות של מחירי בתים.
לכל המדריכים בנושא של למידת מכונה
אהבתם? לא אהבתם? דרגו!
0 הצבעות, ממוצע 0 מתוך 5 כוכבים



המדריכים באתר עוסקים בנושאי תכנות ופיתוח אישי. הקוד שמוצג משמש להדגמה ולצרכי לימוד. התוכן והקוד המוצגים באתר נבדקו בקפידה ונמצאו תקינים. אבל ייתכן ששימוש במערכות שונות, דוגמת דפדפן או מערכת הפעלה שונה ולאור השינויים הטכנולוגיים התכופים בעולם שבו אנו חיים יגרום לתוצאות שונות מהמצופה. בכל מקרה, אין בעל האתר נושא באחריות לכל שיבוש או שימוש לא אחראי בתכנים הלימודיים באתר.
למרות האמור לעיל, ומתוך רצון טוב, אם נתקלת בקשיים ביישום הקוד באתר מפאת מה שנראה לך כשגיאה או כחוסר עקביות נא להשאיר תגובה עם פירוט הבעיה באזור התגובות בתחתית המדריכים. זה יכול לעזור למשתמשים אחרים שנתקלו באותה בעיה ואם אני רואה שהבעיה עקרונית אני עשוי לערוך התאמה במדריך או להסיר אותו כדי להימנע מהטעיית הציבור.
שימו לב! הסקריפטים במדריכים מיועדים למטרות לימוד בלבד. כשאתם עובדים על הפרויקטים שלכם אתם צריכים להשתמש בספריות וסביבות פיתוח מוכחות, מהירות ובטוחות.
המשתמש באתר צריך להיות מודע לכך שאם וכאשר הוא מפתח קוד בשביל פרויקט הוא חייב לשים לב ולהשתמש בסביבת הפיתוח המתאימה ביותר, הבטוחה ביותר, היעילה ביותר וכמובן שהוא צריך לבדוק את הקוד בהיבטים של יעילות ואבטחה. מי אמר שלהיות מפתח זו עבודה קלה ?
השימוש שלך באתר מהווה ראייה להסכמתך עם הכללים והתקנות שנוסחו בהסכם תנאי השימוש.