סיווג בינארי עם PyTorch - מתי ואיך

נשתמש בסיווג בינארי לסיווג דוגמאות לאחת משתי קטגוריות מובחנות. לדוגמה, אבחנה בין תמונות כלבים וחתולים, בחירה האם לזמן שחקן לאימוני הנבחרת ואבחנה בין יינות משובחים ופשוטים. במדריך זה נלמד לסווג נקודות במרחב לאחת משתי קבוצות (אדומים לעומת כחולים) באמצעות ספריית PyTorch בגישה של רגרסיה לוגיסטית logistic regression שעיקר השימוש בה הוא בשביל סיווג בינארי.

יבוא התלויות וקונפיגורציה

את הקוד פיתחתי על המחשב האישי שלי כי אין צורך ב-GPU. אפשר להוריד את המחברת ולהריץ בסביבת colab כדי לחסוך את הצורך להגדיר ולהתקין את סביבת העבודה.

להורדת המחברת עם הקוד אותו נפתח במדריך

נייבא את הספריות הבסיסיות ונגדיל את העקביות באמצעות זריעת random seed:

# import and limit randomness
# to improve reproducibility
import random as rn

seed = 42
rand_state = seed

import os
os.environ['PYTHONHASHSEED'] = '42'

rn.seed(seed)

import numpy as np
np.random.seed(seed)

import torch
torch.manual_seed(seed)

• Numpy משמשת לביצוע חישובים ולעבודה עם מערכים וטנסורים.
• PyTorch היא ספרייה של למידת מכונה בה נשתמש ליצירת המודל.

אין כל צורך ב-GPU ועדיין זה תמיד טוב להגדיר את ה- device ולהשתמש בו בהמשך במטרה להבטיח שהמודל והטנסורים רצים על אותה סביבה:

device = 'cuda' if torch.cuda.is_available() else 'cpu'
print(device)

התוצאה:

cpu

מסד הנתונים

את מסד הנתונים יצרתי באופן סינטטי בעזרת sklearn. הוא מונה 700 נקודות עם מספר זהה של נקודות השייכות לאחת משתי קטגוריות:

# sklearn datasets
import sklearn.datasets as dt

import matplotlib
import matplotlib.pyplot as plt

# set color maps
color_map = plt.cm.get_cmap('RdYlBu')
color_map_discrete = matplotlib.colors.LinearSegmentedColormap.from_list("", ["red","cyan","magenta","blue"])

class_sep = 0.8
n_samples = 700

X,y = dt.make_classification(n_samples=n_samples,
                                 n_features=2,
                                 n_repeated=0,
                                 class_sep=class_sep,
                                 n_redundant=0,
                                 random_state=rand_state)

plt.scatter(X[:,0],
            X[:,1],
              c=y,
              vmin=min(y),
              vmax=max(y),
              s=35,
              cmap=color_map_discrete)

plt.tight_layout()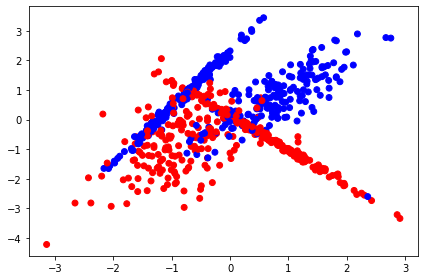

כמה נקודות במסד הנתונים?

len(y)

700

הנקודות שייכות לאחת משתי הקטגוריות: 1 או 0. נדגום את 10 הנקודות הראשונות והאחרונות במסד הנתונים כדי לקבל תחושה:

print(y[:10])
print(y[-10:])

[1 0 1 0 0 1 0 0 0 1]
[1 0 0 0 1 0 1 1 1 1]

מה הפרופורציה של נקודות השייכות לקטגוריה 1?

# ratio of 1s
np.count_nonzero([a==1 for a in y])/len(y)

0.5057142857142857

מה הפרופורציה של נקודות השייכות לקטגוריה 0?

# ratio of 0s
np.count_nonzero([a==0 for a in y])/len(y)

0.4942857142857143

import seaborn as sns
sns.countplot(y)

• יש יתרון קל של 8 נקודות לקטגוריה אחת על פני השנייה (354, 346), אבל בסה"כ סט הנתונים מאוזן עם מספר כמעט זהה לשתי הקטגוריות.

הכנת הנתונים ללמידת מכונה

את הנתונים נחלק לשלוש קבוצות sets. במהלך אימון המודל נשתמש בשתי קבוצות. המודל ילמד מקבוצת האימון train set כאשר בסופו של כל epoch נעריך את ביצועי המודל על נתוני קבוצת ההערכה valuation set. בנתוני קבוצת המבחן test set נשתמש רק אחרי סיום האימון כדי להעריך את יכולות המודל.

החלוקה בפועל של מסד הנתונים נעשות באמעות המתודה train_test_split שיודעת לחלק ל-2 קבוצות. כיוון שדרושים לנו 3, נשתמש במתודה פעמיים ברצף:

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=rand_state, stratify=y)

X_test, X_val, y_test, y_val = train_test_split(X_test, y_test, test_size=0.67, random_state=rand_state, stratify=y_test)

• test_size היא הפרופורציה של החלוקה.
• הפרמטר stratify שומר על הפרופורציות של הקטגוריות.
• אין צורך לציין מפורשות כי ברירת המחדל היא ערבוב הנתונים shuffle. בשביל החזרתיות reproducibility שמשמעותה שכל מי שיעבוד על הקוד יקבל את אותה החלוקה השתמשתי בפרמטר random_state עם המספר הטיפולוגי 42.

מה מספר הנקודות בכל סט לאחר ההפרדה?

print(len(y_train)) # 490
print(len(y_val)) # 141
print(len(y_test)) # 69

נוודא שהפרופורציה של הקטגוריות נשמרה אחרי ההפרדה:

# validate stratification
np.count_nonzero([a==1 for a in y_train])/len(y_train) # 0.506
np.count_nonzero([a==1 for a in y_test])/len(y_test) # 0.507
np.count_nonzero([a==1 for a in y_val])/len(y_val) # 0.504

נשמור עותק מהנתונים לשימוש בהמשך:

# save a copy
X_train_ori = X_train
X_test_ori = X_test
X_val_ori = X_val

y_train_ori = y_train
y_test_ori = y_test
y_val_ori = y_val

נתונים שלא עברו תיאום קנה מידה feature scaling מעכבים את התכנסות המודל לתוצאה במודלים המשתמשים ב-gradient descent, דוגמת רשתות נוירונים ורגרסיה לינארית או לוגיסטית. כדי לפתור את הבעיה נשתמש במתודה StandardScaler של sklearn:

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()

X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
X_val = scaler.transform(X_val)

נשמור עותק מהנתונים שעברו סטנדרטיזציה:

# save a copy
X_train_scaled = X_train
X_test_scaled = X_test
X_val_scaled = X_val

על בסיס 3 קבוצות הנתונים - train, validation, test - נייצר שלושה קלאסים הממשים את הסוג Dataset של PyTorch:

# create a dataset based on a PyTorch class
from torch.utils.data import Dataset
 
class TrainDataset(Dataset):
 def __init__(self):
   # data loading
   self.data = torch.FloatTensor(X_train)
   self.labels = torch.FloatTensor(y_train)
  
 def __getitem__(self, index):
   # dataset[index] to get the index-th item
   return self.data[index], self.labels[index]
 
 def __len__(self):
   # size of dataset
   return len(self.labels)


class ValDataset(Dataset):
 def __init__(self):
   # data loading
   self.data = torch.FloatTensor(X_val)
   self.labels = torch.FloatTensor(y_val)
  
 def __getitem__(self, index):
   # dataset[index] to get the index-th item
   return self.data[index], self.labels[index]
 
 def __len__(self):
   # size of dataset
   return len(self.labels)


class TestDataset(Dataset):
 def __init__(self):
   # data loading
   self.data = torch.FloatTensor(X_test)
   self.labels = torch.FloatTensor(y_test)
  
 def __getitem__(self, index):
   # dataset[index] to get the index-th item
   return self.data[index], self.labels[index]
 
 def __len__(self):
   # size of dataset
   return len(self.labels)

נאתחל את הקלאסים:

# initialize the datasets
train_dataset = TrainDataset()
val_dataset = ValDataset()
test_dataset = TestDataset()

כדי לקבל תחושה לגבי האופן שבו המידע מסודר בקלאסים:

print(train_dataset[0])
print(train_dataset[0][0].shape)
print(train_dataset[0][1].shape)

(tensor([-0.5511,  0.6473]), tensor(0.))
torch.Size([2])
torch.Size([])

• כל נקודת מידע מאופיינת באמצעות 2 קואורדינטות מרחביות (x, y) ולייבל label בינארי 0 או 1.

שימוש בקלאס DataLoader מאפשר לפצל את מסדי הנתונים לאצוות mini-batches במקום לטעון את כל הנתונים בו זמנית מה שעלול להקשות על החישוב והתכנסות המודל:

from torch.utils.data import DataLoader
 
# call the DataLoader to get mini-batches
# separately for each dataset
train_loader = DataLoader(dataset=train_dataset, batch_size=32)
val_loader = DataLoader(dataset=val_dataset, batch_size=32)
test_loader = DataLoader(dataset=test_dataset, batch_size=32)

נקבל תחושה לגבי המידע שמנפקים הקלאסים על ידי כך שנחלץ מהאיטרטור את הדוגמה הראשונה:

n = iter(train_loader).next()
#print(n)
print(n[0].shape)
print(n[1].shape)

torch.Size([32, 2])
torch.Size([32])

המודל

המודל מקבל input שני פיצ'רים - קואורדינטות x ו-y, ופולט output ערך 1 - הוא הקטגוריה החזויה.

המודל מורכב משכבות לינאריות ופונקציות אקטיבציה ReLU. הוספתי שכבת Dropout. המבנה הוא מתכנס - מתחיל מ64 נאורונים ומצטמצם בהדרגה ל-2 כי זה מה שנתן לי את התוצאות הטובות ביותר בניסויים שערכתי.

הערכים שהפונקציה פולטת הם בין 0 ל-1 הודות לפונקצית אקטיבציה סיגמואידית בשכבה המסווגת:

# build the network
import torch.nn as nn # neural network module
 
input_size = 2
output_size = 1

class Classifier(nn.Module):
 def __init__(self):
   # initialize super class
   super(Classifier, self).__init__()
 
   self.classifier = nn.Sequential(
       nn.Linear(input_size, 64),
       nn.Dropout(p=0.1),
       nn.ReLU(),
       nn.Linear(64, 16),
       nn.ReLU(),
       nn.Linear(16, 8),
       nn.ReLU(),
       nn.Linear(8, 4),
       nn.ReLU(),
       nn.Linear(4, output_size)
   )

 def forward(self, x):
   # we use sigmoid activation function for binary classification
   # since it outputs probabilities in the range of 0 to 1
   y_predicted = torch.sigmoid(self.classifier(x))
   return y_predicted

נאתחל את המודל:

model = Classifier()
model.to(device)

בתור loss function נשתמש ב-nn.BCELoss() למדידת מידת השוני בין התוצאות שמנפק המודל ובין התוצאות בפועל במקרה של סיווג בינארי:

# loss function for binary cross entropy
loss_fn = nn.BCELoss()

כאן אני משתמש בפונקציית אקטיבציה מסוג Adam ובפרמטרים באמצעותם קיבלתי את התוצאות הטובות ביותר בניסויים המקדימים:

# optimizer
import torch.optim as optim 
 
learning_rate = 1e-3

# here I use the Adam optimizer with a learning rate of 1e-3
# since this combination gave me the best results in a preliminary experiment
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

תהליך הלמידה

תהליך הלמידה נעשה במסגרת של epochs. בכל epoch המודל לומד מכל נתוני קבוצת האימון train. בסיום הלמידה מעריכים את ביצועי המודל מנתוני קבוצת ההערכה validation.

כל epoch מורכב מארבעה שלבים:

1. Forward pass - המודל מקבל את נתוני האימון training dataset, עורך חישובים ומנפק תחזית משוערת. בשלב זה, נכנסת לפעולה פונקציית loss המחשבת את ההפרש בין ניבויי המודל וערכי האמת.
2. Backward pass - חישוב הנגזרות החלקיות של ה-loss.
3. עדכון המשקולות על פי הגרדיאנטים במטרה להפחית את ה- loss.
4. חוזרים על שלושת הצעדים מספר פעמים מוגדר מראש.

את הקוד המשמש להרצת תהליך האימון כינסתי לתוך פונקציה שקראתי לה train_and_validate המחזירה את נתוני ה-loss של נתוני האימון train וההערכה validation:

# train in mini-batches
def train_and_validate(num_epochs, train_loader, val_loader):
  # track data
  epochs = []

  # the training loss as the model trains
  train_losses = []
  # the validation loss as the model trains
  valid_losses = []
  # the average training loss per epoch as the model trains
  avg_train_losses = []
  # the average validation loss per epoch as the model trains
  avg_valid_losses = []

  for epoch in range(num_epochs):
    # training
    # one mini-batch at a time
    for x_batch, y_batch in train_loader:
      # send to the same device as the model
      x_batch = x_batch.float().to(device)
      y_batch = y_batch.float().to(device)
  
      # the actual training
      # set model to "train" mode
      model.train()

      # make predictions
      yhat = model(x_batch)

      # computes loss
      loss = loss_fn(yhat, y_batch.unsqueeze(1))

      # backward pass:
      # back propagation and calculate the gradients
      loss.backward()

      # updates the weights
      optimizer.step()
        
      # record training loss
      train_losses.append(loss.item())

      # before the next iteration we have to be careful
      # we need to empty our gradients
      optimizer.zero_grad()


    # once finished training
    # it's time for evaluation

    # for validation we must turn off gradient computation
    with torch.no_grad():
      # several mini-batches in a single epoch
      for x_val, y_val in val_loader:
        # send to the same device as the model
        x_val = x_val.float().to(device)
        y_val = y_val.float().to(device)

        # set model to "validation" mode
        model.eval()

        # make predictions
        yhat = model(x_val)

        # find validation loss
        val_loss = loss_fn(yhat, y_val.unsqueeze(1))
        
        # record validation loss
        valid_losses.append(val_loss.item())


    # track epochs and losses
    train_loss = np.average(train_losses)
    valid_loss = np.average(valid_losses)
    avg_train_losses.append(train_loss)
    avg_valid_losses.append(valid_loss)

    print(f'epoch {(epoch+1)}/{num_epochs}, val_loss: {valid_loss}, loss: {train_loss}')
    
    # clear lists to track next epoch
    train_losses = []
    valid_losses = []
  
  print("finished training")
  return epochs, avg_train_losses, avg_valid_losses

נאמן את המודל במסגרת של 150 epochs:

# train the model
num_epochs = 150
epochs, losses, val_losses = train_and_validate(num_epochs, train_loader, val_loader)

בסיום תהליך הלמידה הפונקציה החזירה רשימה של ערכי loss עבור נתוני האימון והוולידציה. התרשים הבא עוקב אחר השינוי בערכי ה-loss כפונקציה של מספר ה-epochs:

# visualize the loss as the network trained
fig = plt.figure(figsize=(10,8))
plt.plot(range(1,len(losses)+1),losses, label='Training Loss')
plt.plot(range(1,len(val_losses)+1),val_losses,label='Validation Loss')

plt.xlabel('epochs')
plt.ylabel('loss')
plt.ylim(0, 0.7) # consistent scale
plt.xlim(0, len(losses)+1) # consistent scale
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
fig.savefig('loss_plot.png', bbox_inches='tight')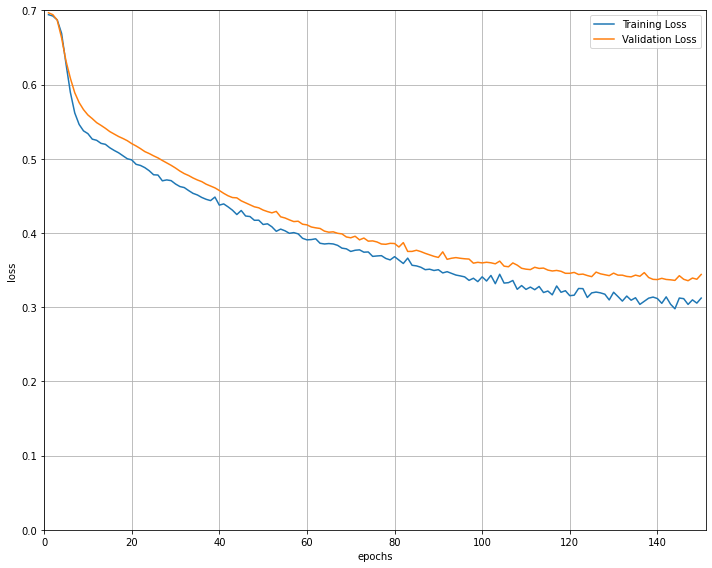

הערכת התוצאות

לאחר שסיימנו את אימון המודל נפיק ממנו ניבויים עבור סט ה- test שהחזקנו עד עכשיו בצד:

# list of predictions
y_pred_list = []

# list of test data
x_evals = []

# list of labels data
y_evals = []

# must be in "validation" mode
model.eval()

with torch.no_grad():
    # mini-batches
    for x_test, y_test in test_loader:
        # send to the same device as the model
        x_test = x_test.float().to(device)
        y_test = y_test.float().to(device)
        x_evals.append(x_test)
        y_evals.append(y_test)
        
        # predict
        y_test_pred = model(x_test)
        y_pred_tag = torch.round(y_test_pred)
        y_pred_list.append(y_pred_tag.cpu().numpy())
        
        # calculate the test loss
        # test_loss = loss_fn(y_test_pred, y_test.unsqueeze(1))

y_pred_list = [a.squeeze().tolist() for a in y_pred_list]
x_test_list = [a.squeeze().tolist() for a in x_evals]
y_test_list = [a.squeeze().tolist() for a in y_evals]

כיוון שהתוצאה היא רשימה של רשימות, הפונקציה הבאה תעזור לנו לשטח לרשימה אחת:

# make a flat list out of a list of lists
def flatten(x):
    f = [item for sublist in x for item in sublist]
    return f

נשווה את ניבויי המודל אם התוצאות בפועל באמצעות confusion matrix:

from sklearn.metrics import confusion_matrix, classification_report
confusion_matrix(flatten(y_test_list), flatten(y_pred_list))

array([[32,  2],
       [ 7, 28]])

• השורות מציגות את קטגוריות האמת והעמודות את תחזיות המודל.
• נראה שהמודל נוטה לשגות יותר ולסווג נקודות השייכות לקטגוריה 1 בתור קטגוריה 0 מאשר הפוך (7 נקודות לעומת 2).

הקוד הבא יאפשר לנו לזהות את מיקום 9 הנקודות שהמודל שגה בזיהוי שלהם:

x_wrong = []
y_wrong = []
for i, prediction in enumerate(y_pred_list_flattened):
    if y_test_list_flattened[i] != prediction:
        print(str(i), str(y_test_list_flattened[i]), str(prediction), X_test_ori[i])
        x_wrong.append(X_test_ori[i][0])
        y_wrong.append(X_test_ori[i][1])

0 1.0 0.0 [-0.08396673 -0.17146166]
18 0.0 1.0 [0.02734225 0.62238271]
22 1.0 0.0 [-0.48217015 -0.50207176]
34 1.0 0.0 [-0.74049375 -1.13258076]
43 1.0 0.0 [ 2.3578821  -2.60001986]
50 1.0 0.0 [-0.25067536 -0.45531601]
57 1.0 0.0 [ 0.20541416 -0.68978679]
58 0.0 1.0 [-0.17254362  0.90607463]
62 1.0 0.0 [-0.67096412 -0.62712244]

X,y = dt.make_classification(n_samples=n_samples,
                                 n_features=2,
                                 n_repeated=0,
                                 class_sep=class_sep,
                                 n_redundant=0,
                                 random_state=rand_state)

plt.scatter(X[:,0],
            X[:,1],
              c=y,
              vmin=min(y),
              vmax=max(y),
              s=35,
              cmap=color_map_discrete)

plt.scatter(x_wrong, y_wrong, marker='*', color='yellow', s=200, label='wrong', alpha=0.6)
plt.legend()
plt.tight_layout()

בתרשים הבא הנקודות שהמודל שגה בסיווגם מסומנות בכוכבית:

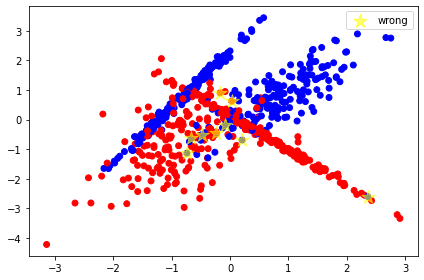
• המודל שגה במקרים עמומים היכן שהנקודות יושבות בין הקטגוריות או במקרים של outliers כאשר נקודה אינה ממוקמת בין הנקודות של הקטגוריה. לדוגמה, הכוכבית הימנית ביותר שבה נקודה כחולה ממוקמת בתוך סביבה אדומה לגמרי.

נוסף לשיעור הדיוק (accuracy) חשוב להעריך את ביצועי המודל המסווג באמצעות מדד f1 הלוקח בחשבון את המדדים recall ו-precision:

print(classification_report(flatten(y_test_list), flatten(y_pred_list)))

         precision    recall  f1-score   support

         0.0       0.82      0.94      0.88        34
         1.0       0.93      0.80      0.86        35

    accuracy                           0.87        69
   macro avg       0.88      0.87      0.87        69
weighted avg       0.88      0.87      0.87        69

אלגוריתם KNN k-Nearest Neighbors הוא מוכר ופופולרי מאוד לצרכים של סיווג בינארי לכן נשווה את הביצועים של המודל אותו פיתחנו במדריך אליו:

from sklearn.neighbors import KNeighborsClassifier
neigh = KNeighborsClassifier(n_neighbors=2)
neigh.fit(X_train_scaled, y_train)

KNeighborsClassifier(n_neighbors=2)

נעביר לו את הנתונים שעברו סטנדרטיזציה כדי לשפר את יכולת הניבוי:

y_pred_list = neigh.predict(X_test_scaled)

נעריך את ביצועי המודל KNN:

from sklearn.metrics import confusion_matrix, classification_report
confusion_matrix(y_test_ori, y_pred_list)

array([[33,  1],
       [14, 21]])

print(classification_report(y_test_ori, y_pred_list))

precision    recall  f1-score   support

           0       0.70      0.97      0.81        34
           1       0.95      0.60      0.74        35

    accuracy                           0.78        69
   macro avg       0.83      0.79      0.78        69
weighted avg       0.83      0.78      0.78        69

המודל של sklearn נתן ביצועים פחות טובים ממודל הלמידה העמוקה אותו פיתחנו במדריך על בסיס PyTorch. לדוגמה, במדד accuracy עם 0.78 לעומת 0.87 . כנ"ל במדדי f1.

המסקנה היא שבמקרים שבהם כל אחוז חשוב צריך לשקול למידה עמוקה למרות שהעמדת המודל קשה משמעותית יותר מאשר עבודה עם מודלים של sklearn.

להורדת המחברת עם הקוד אותו פיתחנו במדריך

אולי גם זה יעניין אותך

10 דברים שחובה להכיר כשעובדים עם טנסורים של pytorch

רגרסיה קווית להערכת מחירי דירות באמצעות PyTorch ולמידת מכונה

סיווג תמונות באמצעות למידת מכונה מבוססת PyTorch

לכל המדריכים בסדרה על למידת מכונה

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים