יישום רשימת סמיכויות adjacency list - חלק ב בסדרה על גרפים

במדריך הקודם בסדרה על גרפים בפייתון הסברנו מהו גרף והדגמנו על התרשים:

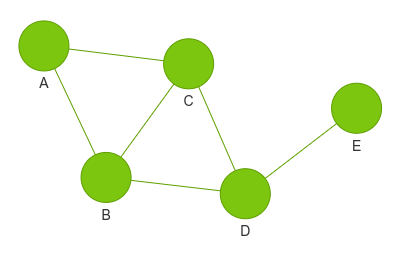
בתרשים יש 5 צמתים (vertex, nodes):

V = [A, B, C, D, E]

ו-6 קשתות (edges) המחברות בין הצמתים. לדוגמה, "A" מחובר ל-"B", וגם "A" מחובר ל-"C". נציין את כל הקשתות ברשימה אחת:

E = [(A, B), (A, C),  (B, C), (B, D), (C, D), (D, E)]

את הגרף נייצג בתור מילון של פייתון:

adjacency_list = {}

בתוך המילון יש לנו צומת "A" שיש לו צמתים המחוברים אליו בקשתות. את "A" נייצג בתור מפתח key ואת רשימת הצמתים הסמוכים אליו נרשום בתוך רשימה (בין סוגריים מרובעים):

adjacency_list = {
    "A": []
}

הצמתים הסמוכים ל-"A" הם "B" ו-"C". נשייך גם אותם למילון:

adjacency_list = {
    "A": ["B", "C"]
}

הצמתים הסמוכים ל-"B" הם "A", "C" ו-"D". נוסיף גם אותם:

adjacency_list = {
    "A": ["B", "C"],
    "B": ["A", "C", "D"]
}

נוסיף את "C":

adjacency_list = {
    "A": ["B", "C"],
    "B": ["A", "C", "D"],
    "C": ["A", "B", "D"],
}

נוסיף את "D" ו-"E":

adjacency_list = {
    "A": ["B", "C"],
    "B": ["A", "C", "D"],
    "C": ["A", "B", "D"],
    "D": ["B", "C", "E"],
    "E": ["D"]
}

ננסה לשלוף את המידע על השכנים של אחד הצמתים. לדוגמה, הצומת של "C":

adjacency_list["C"]

התוצאה:

["A", "B", "D"]

אם נרצה להוסיף קשת. לדוגמה בין "E" ל-"C" אז נוסיף אותם לרשימת השכנים:

adjacency_list["C"].append("E")
adjacency_list["E"].append("C")

• הקשר הוא דו כיווני כיוון שהגרף אינו מכוון undirected. לפיכך, הוספנו את "C" לרשימה של "E" ואת "E" לרשימה של "C". אם הקשת הייתה מכוונת אז היינו צריכים להוסיף רק לאחד.

נדפיס את הרשימה לאחר השינוי:

print(adjacency_list)

מבנה של Adjacency list

ניצור קלאס Graph לארגון הגרף באמצעות adjacency list:

class Graph: 
    def __init__(self, nodes=None, directed=False): 
        # Initialize a graph with a list of nodes and a directed flag
        self.nodes = nodes if nodes is not None else []
        self.directed  = directed

        self.adjacency_list = {}

        for node in self.nodes:
            # Create an empty adjacency list for each node
            self.adjacency_list[node] = []

• הפונקציה מקבלת 2 ארגומנטים: nodes, רשימת צמתים של הגרף ו-directed אם הגרף מכוון.
• מבנה הגרף יתחיל ללא קישורים בין ה-nodes לכן נתחיל מרשימת סמיכויות adjacency_list שהיא מילון ריק.
• הפונקציה עוברת על כל אחד מה-nodes של הגרף ומאתחלת אותו על ידי הוספה שלו כמפתח ל-adjacency list כאשר הערך שמקבל המפתח בתחילה הוא רשימה ריקה.

נוסיף לקלאס Graph מתודה add_node() לצורך הוספת node לגרף:

def add_node(self, node): 
    # Add a new node to the graph
    if node not in self.nodes:
        self.adjacency_list[node] =  []
        self.nodes.append(node)

• המתודה add_node() מקבלת ארגומנט node שהוא ערך הצומת החדש.
• המתודה בודקת שה-node לא קיים ברשימת הצמתים nodes כדי למנוע כפילויות.
• אם ה-node לא קיים המתודה מוסיפה אותו לרשימת ה-nodes ול-adjacency_list.

המתודה add_edge() תאפשר הוספת קשתות edges בין שני nodes באופן מכוון או בלתי מכוון:

def add_edge(self, source, destination):
        # Check if the source and destination nodes exist in the graph
        if source not in self.nodes:
            # Add the source node to the graph if it does not exist.
            self.add_node(source)

        if destination not in self.nodes:
            # Add the destination node to the graph if it does not exist.
            self.add_node(destination)

        # Add the edge to the source node's adjacency list
        self.adjacency_list[source].append(destination)

        # If the graph is not directed, add the edge to the destination node's adjacency list as well
        if not self.directed:
            self.adjacency_list[destination].append(source)

• המתודה add_edge() מוסיפה קשת edge לגרף. היא מקבלת שני ארגומנטים: source ו-destination המייצגים את 2 הצמתים ביניהם מקשרת הקשת.
• המתודה קודם כל בודקת אם הצמתים קיימים בגרף. אם הם אינם קיימים, היא מוסיפה אותם.
• המתודה מתחשבת בכווניות של הגרף. היא תמיד תוסיף קשת מ-source ל-destination. אם הגרף אינו מכוון היא תוסיף גם קשת הפוכה מ-destination ל-source.

נוסיף מתודה ליצירת רשימת סמיכויות generate_adjacency_list():

def generate_adjacency_list(self, edges):

    # Check if the edges list is not empty
    if edges:

        # Iterate over the edges list
        for edge in edges:

            # Get the source and destination nodes from the edge
            source, destination = edge

            # Add the edge to the graph
            self.add_edge(source, destination)

        # Return the graph's adjacency list
        return self.adjacency_list

    else:

        # Return an empty dictionary
        return {}

• תפקיד המתודה generate_adjacency_list() הוא לייצר רשימת סמיכויות. המתודה מקבלת ארגומנט edges שהוא רשימת קשתות.
• המתודה בודקת אם רשימת הסמיכויות אינה ריקה. אם ריקה אז המתודה מחזירה מילון ריק.
• בהמשך, המתודה עוברת בלולאה על הקשתות ומפעילה את המתודה add_edge() להוספת קשת בכל פעם שהיא רצה.
• לבסוף, המתודה מחזירה את רשימת הסמיכויות של הגרף.

נדפיס את המידע בקלאס באמצעות מתודת הקסם הפייתונית __repr__ בה נשתמש כדי לייצג אובייקט באופן שניתן אח"כ להשתמש בו כדי לשחזר את האובייקט.

def __repr__(self):

    # Get the list of nodes in the graph
    nodes = list(self.adjacency_list.keys())

    # Sort the nodes in alphabetical order
    nodes.sort()

    # Create a string representation of the graph's adjacency list
    adjacency_repr = ", ".join([f"{node}: {self.adjacency_list[node]}" for node in nodes])

    # Return the string representation of the graph
    return f"Graph({adjacency_repr})"

• המתודה __repr__ היא מתודת קסם של פייתון המשמשת לייצוג אובייקט כמחרוזת. הייצוג כולל את רשימת הצמתים של הגרף ואילו צמתים קשורים ביניהם.

עכשיו הכל ביחד:

class Graph:
    def __init__(self, nodes=None, directed=False):
        # Initialize a graph with a list of nodes and a directed flag
        self.nodes = nodes if nodes is not None else []
        self.directed = directed

        self.adjacency_list = {}

        for node in self.nodes:
            # Create an empty adjacency list for each node
            self.adjacency_list[node] = []

    def add_node(self, node):
        # Add a new node to the graph
        if node not in self.nodes:
            self.adjacency_list[node] = []
            self.nodes.append(node)

    def add_edge(self, source, destination):
        # Check if the source and destination nodes exist in the graph
        if source not in self.nodes:
            # Add the source node to the graph if it does not exist.
            self.add_node(source)

        if destination not in self.nodes:
            # Add the destination node to the graph if it does not exist.
            self.add_node(destination)

        # Add the edge to the source node's adjacency list
        self.adjacency_list[source].append(destination)

        # If the graph is not directed, add the edge to the destination node's adjacency list as well
        if not self.directed:
            self.adjacency_list[destination].append(source)


    def __repr__(self):
        # Get the list of nodes in the graph
        nodes = list(self.adjacency_list.keys())

        # Sort the nodes in alphabetical order
        nodes.sort()

        # Create a string representation of the graph's adjacency list
        adjacency_repr = ", ".join([f"{node}: {self.adjacency_list[node]}" for node in nodes])

        # Return the string representation of the graph
        return f"Graph({adjacency_repr})"

לצורך בדיקה ניצור אובייקט Graph ונדפיס אותו:

# Example usage
graph = Graph()
graph.add_edge('A', 'B')
graph.add_edge('A', 'C')
graph.add_edge('B', 'C')
graph.add_edge('B', 'D')
graph.add_edge('C', 'D')
graph.add_edge('D', 'E')

print(repr(graph))

התוצאה:

Graph(A: ['B', 'C'], B: ['A', 'C', 'D'], C: ['A', 'B', 'D'], D: ['B', 'C', 'E'], E: ['D'])

יתרונות וחסרונות של Adjacency list

היתרון המרכזי של רשימת סמיכויות על פני מטריקס הוא עבור גרפים שיש בהם מעט קשתות יחסית למספר הצמתים sparse graphs כי אין צורך להקצות מקום בזיכרון לקשרים פוטנציאליים בין צמתים. לגרפים צפופים השימוש ברשימת סמיכויות הוא פחות מומלץ בגלל שהחיסכון בזכרון הוא פחות משמעותי ואז הוצאות תקורה overhead עבור הרשימה שמחזיק כל צומת הופכים לגורם המכריע.

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

יישום תורת הגרפים בפייתון - חלק א

יישום רשימת סמיכויות adjacency list - חלק ב בסדרה על גרפים

חלק ג בסדרה על גרפים - Pyviz - ספרייה להצגת גרפים אינטראקטיביים

הבנת אלגוריתם חיפוש לרוחב - BFS - סריקה של גרפים ומציאת הנתיב הקצר ביותר

אלגוריתם חיפוש לעומק DFS - מהבנה ליישום

אלגוריתם דייקסטרה Dijkstra למציאת הנתיב הקצר ביותר בגרף ממושקל

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים