ערימה בינארית Binary Heap ותור עדיפויות Priority Queue

Binary heap ערימה בינארית היא מבנה נתונים רב עוצמה ויעיל המשמש במדעי המחשב לשמירת אוסף של פריטים עם גישה מהירה לפריט הגדול או הקטן ביותר. ערימה Heap היא בעלת תפקיד מכריע בפתרון בעיות חישוביות שונות.

ערימה heap היא מבנה נתונים מיוחד המארגן אוסף של פריטים בדרך מסוימת. הוא משמש בדרך כלל כדי לנהל ולגשת ביעילות לפריט הגדול (max-heap) או הקטן (min-heap).

אחד מסוגי ה-heap הינו ערימה בינארית binary heap בו יעסוק מדריך זה.

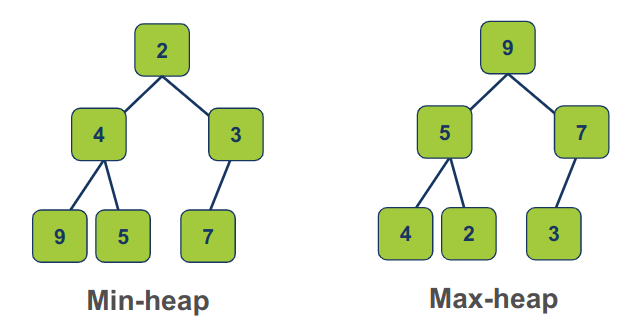
ערימה בינארית binary heap היא עץ בינארי המציית לכללים המסדירים את ארגון הצמתים שלו. בערימת מקסימום (max-heap), לכל צומת יש ערך גדול יותר או שווה לצמתים הילדים שלו, מה שמבטיח שצומת השורש מכיל את הפריט הגדול ביותר בערימה. לעומת זאת, בערימת מינימום (min-heap), לכל צומת יש ערך קטן יותר או שווה לצמתים הילדים שלו, וכתוצאה מכך צומת השורש מכיל את הפריט הקטן ביותר.

יתרון עיקרי לשימוש בערימה הוא יכולתה לאחזר במהירות את הפריט הגדול או הקטן ביותר. זה הופך אותה לפתרון מועדף ליישומי תור עדיפויות (priority queue), שם פריטים מעובדים על פי מידת הקדימות שלהם - קודם הדחוף ביותר. בנוסף, ערימות משמשות במגוון אלגוריתמים, כמו אלגוריתם דייקסטרה (Dijkstra's algorithm) למציאת הנתיב הקצר ביותר בגרפים, ולמיון פריטים ביעילות (heapsort).

אם אחד היתרונות המרכזיים של ערימה הוא האפשרות לאחזר במהירות את הפריט הגדול או הקטן ביותר אז הרי זה דבר שניתן להשיגו באותה מידה של יעילות אם משתשמשים במערך מסודר כיוון שאחזור הפריט הקיצוני דורש סיבוכיות זמן קבועה O(1) בשני המקרים. אולם, ההבדל המשמעותי הוא שמשך הביצוע של פעולות הכרחיות כדוגמת הוספת פריט או מחיקת השורש עשויות לארוך עד משך זמן O(N) במקרה של מערך אבל במקרה של ערימה בינארית אותם פעולות דורשות סיבוכיות זמן קצרה בהרבה של O(log N) בגלל האופי הבינארי של מבנה הנתונים המפחית במחצית את מספר הפריטים האפקטיבי בכל צעד של ביצוע הפעולה. לכן, במקרים בהם המטרה היא לבצע פעולות על פריטים קיצוניים כמו מציאת הפריט המקסימלי/מינימלי או הכנסה והסרה של פריטים בצורה יעילה, ערימה בינארית מסודרת היא בחירה טובה ויעילה יותר מאשר מערך.

מדריך זה פותח בהבנת המושגים הבסיסיים הדרושים להבנת heap, לאחר מכן תלמד איך לפתח פונקציות לביצוע הפעולות הנפוצות ביותר על ערימה בינארית ללא עזרת ספרייה, לקראת סוף המדריך תמצא הסבר איך להשתמש בספריית heapq של פייתון, ולבסוף תראה כיצד ליישם תור עדיפויות מבוסס ערימה בינארית.

במדריך זה נדון ונדגים כמה מהפעולות הנפוצות ביותר שניתן לבצע באמצעות ערימה heap:

• heapify - סידור מחדש של הערימה כדי לשמור על תכונות הערימה.
• הכנסה - הוספת פריט חדש לערימה.
• מציאת מקסימום (או מציאת מינימום) - מציאת פריט מקסימלי של ערימת מקסימום, או פריט מינימלי של ערימת מינימום.
• מחיקה - מחיקת פריט מהערימה.
• הוצאת מקסימום/מינימום - החזרת ומחיקת הפריט המקסימלי/המינימלי מערימת מקסימום/מינימום.

לפני שנסביר את הפעולות שניתן לבצע על heaps נניח את היסודות עליהם נבסס את הבנת מבנה הנתונים.

הצגת עץ בינארי באמצעות מערך

הצגת עץ בינארי באמצעות מערך היא טכניקה נפוצה המאפשרת אחסון וסריקה יעילים של העץ. היא פועלת על ידי ניצול תכונות של עצים בינאריים ומיפוי צמתים של העץ אל פריטים של מערך חד ממדי. הנה דוגמה פשוטה הממחישה את הנושא:

נתון העץ הבינארי הבא:

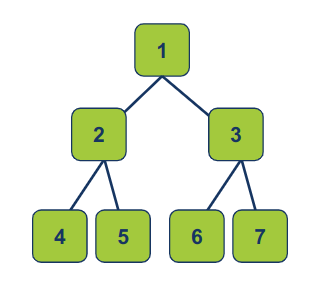
אשר מיוצג על ידי המערך:

[1, 2, 3, 4, 5, 6, 7]

הכללים להקצאת האינדקסים של המערך לצמתים הם:

• השורש (שהוא הפריט הקטן או הגדול ביותר) ימצא באינדקס 0
• עבור כל הורה שמיקומו אינדקס i, ילדו השמאלי יימצא באינדקס 2*i+1 וילדו הימני באינדקס 2*i+2
• אפשר גם הפוך, אם ילד נמצא ב-i אז ההורה שלו יימצא ב- floor((i-1) / 2)

נחזור לדוגמה שלנו:

• צומת השורש (1) נמצא באינדקס 0, והוא מהווה הורה של הצמתים 2 ו-3.
• צומת 2 הילד השמאלי של השורש נמצא באינדקס 2*0 + 1 = 1.
• צומת 3 הילד הימני של השורש נמצא באינדקס 2*0 + 2 = 2.
• צומת 4, ילדו השמאלי של צומת 2, נמצא באינדקס 2*1 + 1 = 3.
• צומת 5, ילדו הימני של צומת 2, נמצא באינדקס 2*1 + 2 = 4.
• צומת 6, ילדו השמאלי של צומת 3, נמצא באינדקס 2*2 + 1 = 5.
• צומת 7, ילדו הימני של צומת 3, נמצא באינדקס 2*2 + 2 = 6.

אם חסרים פריטים אז נציב במקומם null. לדוגמה:

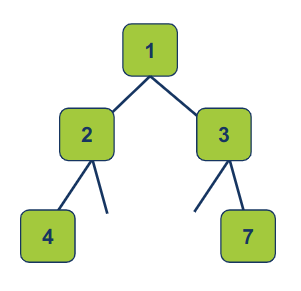
כך יראה המערך:

[1, 2, 3, 4, null, null, 7]

עץ בינארי מלא ועץ בינארי שלם

עץ בינארי מלא full ועץ בינארי שלם complete הם שני סוגים של עצים בינאריים, כל אחד עם מאפיינים ייחודיים:

1. עץ בינארי מלא full

   • בעץ בינארי מלא, לכל צומת יש 0 או 2 ילדים. במילים אחרות, לכל צומת בעץ יש ילד שמאלי וימני, או שאין לו ילדים בכלל.
   • צמתים עלים (צמתים ללא ילדים) נמצאים באותה רמה, בעוד לכל הצמתים הפנימיים יש שני ילדים. תכונה זו הופכת את העץ ל"מלא" מכיוון שהוא ממלא את כל הרמות ככל האפשר.

   דוגמה לעץ בינארי מלא:

   

   דוגמה נוספת לעץ בינארי מלא:

   

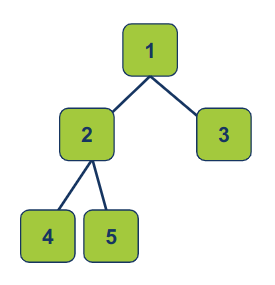
2. עץ בינארי שלם complete

   • עץ בינארי שלם הוא עץ בינארי שבו כל הרמות, למעט אולי הרמה האחרונה, מלאות, וצמתי הרמה האחרונה לא חייבות שיהיו להם ילדים אבל אם יש ילדים אז מוסיפים אותם משמאל לימין left-justified.
   • במילים אחרות, כל הרמות ממולאות משמאל לימין, למעט הרמה האחרונה, שיכולה להכיל פחות צמתים אך צריכה להיות מלאה משמאל ככל האפשר.

   דוגמה לעץ בינארי שלם:

   

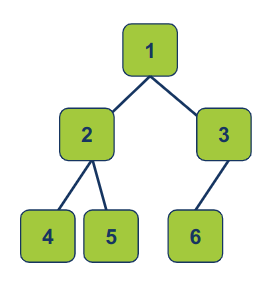
   עץ זה מלא ושלם:

   

   העץ הבא מלא אך אינו שלם:

   

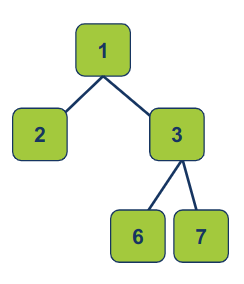
לסיכום, עץ בינארי מלא מאופיין בכך שכל צומת יש לו 0 או 2 ילדים, בעוד שעץ בינארי שלם מוגדר על ידי כך שכל הרמות מלאות משמאל לימין, למעט הרמה האחרונה.

עץ בינארי שלם מוגדר על ידי כך שכל הרמות מלאות משמאל לימין, למעט הרמה האחרונה.

מה הגובה של עץ בינארי שלם?

גובה של עץ הוא אורך הנתיב הארוך ביותר מהשורש לצומת עלה.

את גובהו של עץ בינארי שלם ניתן לחשב באמצעות הנוסחה:

height = floor(log2(n))

• כאשר n הוא מספר הצמתים.

לדוגמה, נבחן עץ בינארי שלם עם 7 צמתים:

נציב n=7 לתוך הנוסחה:

height = floor(log2(7)) 
      = floor(2.81) 
      = 2

• התוצאה מלמדת שגובהו של עץ בינארי שלם זה הוא 2.

ככלל, גובהו של עץ בינארי שלם שיש בו n צמתים הוא log2(n) מה שהופך אותו למאוד מתאים ליישומים של אחזור הפריט הקיצוני (הנמוך/הגבוה ביותר).

התנאים להם חייבת לציית ערימה בינארית heap

ערימה בינארית חייבת לציית לשני תנאים:

1. Heap חייב להיות עץ בינארי שלם

   • Heap חייב להיות עץ בינארי שלם, כלומר כל רמה למעט הרמה התחתונה ביותר מלאה, וצמתי הרמה התחתונה ביותר ממוקמים ככל האפשר משמאל.
   • תכונה זו של שלמות חיונית לאחסון יעיל של ערימת נתונים בייצוג מערך. הצמתים השמאליים ביותר ברמה התחתונה ממולאים באופן רציף, מה שמבטיח שצמתי העץ יהיו מכוונים בקלות לאינדקסים של המערך.

2. Heap חייב לציית לתכונת סדר הערימה Heap order property

   • עץ הערימה חייב לעמוד בתכונת סדר הערימה Heap order property (ידוע גם כ- Heap Invariant), אשר מחלקת אותו לשני סוגים: ערימת מקסימום (max-heap) וערימת מינימום (min-heap).
   • בערימת מקסימום, עבור כל צומת A, הערך של A גדול יותר או שווה לערכי ילדיו (אם קיימים). זה אומר שהפריט המקסימלי נמצא בצומת השורש, ולכל צומת הורה יש ערך גדול יותר או שווה לילדיו.
   • בערימת מינימום, עבור כל צומת A, הערך של A קטן יותר או שווה לערכי ילדיו (אם קיימים). זה אומר שהפריט המינימלי נמצא בצומת השורש, ולכל צומת הורה יש ערך קטן יותר או שווה לילדיו.

לסיכום, כדי שעץ בינארי יהיה heap, הוא חייב להיות עץ בינארי שלם complete ולציית לתכונת סדר הערימה heap invariant. תכונות אלה הופכות את ה-heap למבנה נתונים שימושי לצורך גישה ושינוי של הפריט המקסימלי או המינימלי באוסף הפריטים.

כדי שעץ בינארי יהיה heap, הוא חייב להיות עץ בינארי שלם complete ולציית לתכונת סדר הערימה heap invariant.

ייצוג של עץ בינארי שלם באמצעות מערך

הקצאת טווח האינדקסים עבור צמתים פנימיים ועלים בעץ בינארי המורכב מ- N פריטים עוקב אחר הדפוס:

• צמתים פנימיים תופסים את טווח האינדקסים מ-`0` עד `floor(N/2) - 1`.
• העלים בעץ בינארי תופסים את טווח האינדקסים מ-`floor(N/2)` עד `N - 1`.

לדוגמה, בעץ הבינארי:

המיוצג במערך:

[1, 2, 3, 4, 5, 6, 7]

הצמתים הפנימיים הם:

[1, 2, 3]

העלים הם:

[4, 5, 6, 7]

הסיבה לסידור זה היא שבעץ בינארי מלא, הצמתים הפנימיים ממוקמים ברמות העליונות של העץ, בעוד שהעלים ממוקמים בשכבות הנמוכות. זה מבטיח שהעץ שומר על תכונת השלמות, כאשר הרמה האחרונה ממולאת משמאל לימין.

ייצוג של heap באמצעות עץ בינארי ומערך

בערימת מינימום (min-heap), פריט הורה הוא קטן יותר או שווה לילדיו.

את המערך:

[0, 1, 2, 3, 4, 5, 6] 

נייצג באמצעות עץ בינארי שלם המדגים ערימת מינימום min-heap:

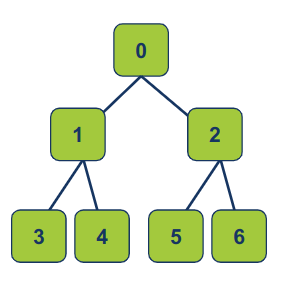
בערימת מקסימום (max-heap), פריט הורה הוא גדול יותר או שווה לילדיו.

לדוגמה, ערימת מקסימום max-heap:

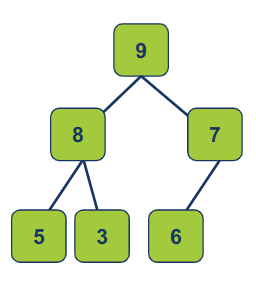
אותה נייצג באמצעות מערך:

[9, 8, 7, 5, 3, 6]

הכנסה של פריט ו-heapify up

כשאנחנו מכניסים פריט חדש insert ל-heap אנחנו צריכים לקחת בחשבון את 2 תכונות הערימה:

• תכונת הערימה heap invariant המחייבת שההורה תמיד יהיה גדול מילדיו ב-max-heap  (או קטן מילדיו ב-min-heap).
• שמירה על שלמות העץ הבינארי.

ניקח לדוגמה את ה min-heap הבא:

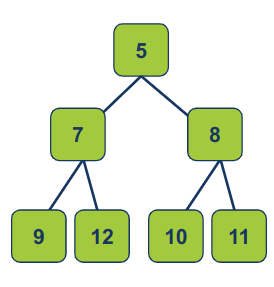
את הצומת החדש נוסיף הכי שמאלה שאפשר. אם יש מקום ברמה האחרונה אז נוסיף אותו הכי שמאלה שאפשר לרמה האחרונה ואם אין מקום ברמה האחרונה נרד רמה ונוסיף בעמדה הכי שמאלית.

את תהליך ההוספה נבצע "משמאל לימין ומלמעלה למטה": "משמאל לימין" בתוך רמה לא מלאה, ואם הרמה מלאה לגמרי נרד רמה אחת למטה ונתחיל שם מהעמדה הכי שמאלית.

נוסיף צומת שערכו 6:

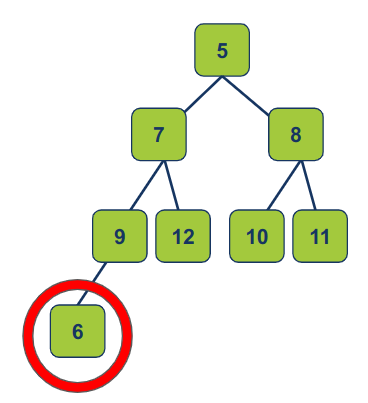
נשווה את הצומת שזה עתה הוספנו להורה שלו כדי לבדוק האם ההוספה לא גרמה להפרת תכונת הערימה. מכיוון שהילד קטן מההורה, הופרה תכונת הערימה הדרושה ל- min-heap. על כן נחליף בין ההורה לבין הילד:

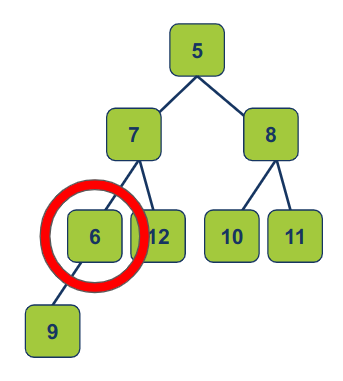
התהליך שבו אנו משווים בין הורה לילד ומחליפים במידת הצורך בין ההורה לילד תוך דחיפת הילד כלפי מעלה לכיוון השורש מכונה heapify up

אחרי ההחלפה נחזור על התהליך. במקרה שלנו, 6 קטן מההורה שלו 7 אז נחליף ביניהם:

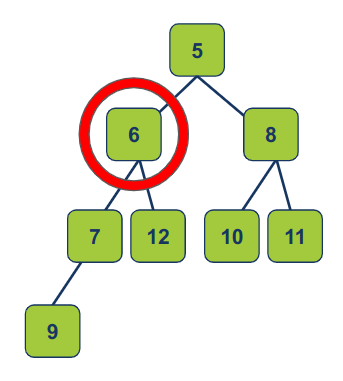
אחרי שהגענו למצב שהילד גדול מההורה שלו נעצור את התהליך כיוון שהצלחנו להביא את העץ למצב שהוא מקיים את תכונת הערימה min-heap לפיה כל הורה קטן מילדיו.

התהליך שבו אנו משווים בין הורה לילד ומחליפים במידת הצורך בין ההורה לילד מכונה heapify והינו תהליך רקורסיבי החוזר על עצמו כל עוד צריך עד לעצירה באחד מ-2 תנאי הבסיס:

1. הגעה לצומת עלה.
2. הצומת הנוכחי מקיים את תנאי ה-heap-invariant. דהיינו, כל הורה גדול מילדיו במקרה של max-heap או כל הורה קטן מילדיו במקרה של min-heap.

במקרה הגרוע ביותר, נוסיף צומת הקטן מכל פריטי ערימת min-heap ואז נצטרך לעשות החלפות עד שנביא את הצומת לראש הערימה:

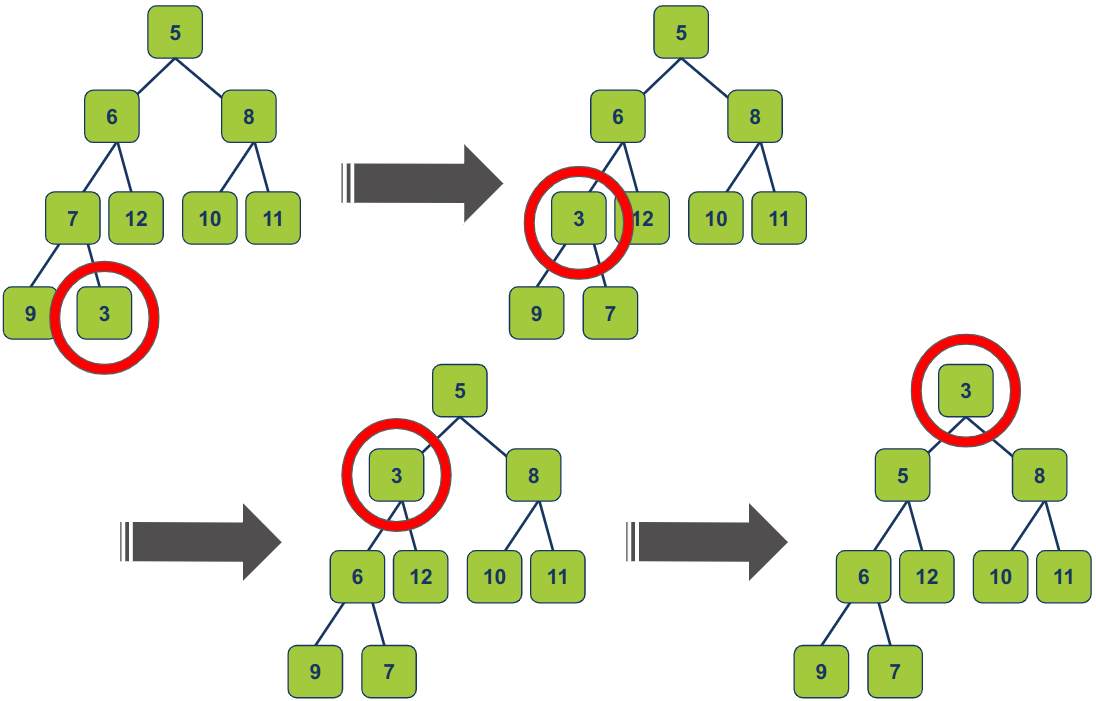
לסיכום, הוספנו פריט לסוף הערימה מה שגרם להפרת תכונת הערימה heap-invariant כיוון שהפריט שהוספנו היה קטן מההורה שלו בערימת מינימום. כדי לתקן את המצב ביצענו תהליך של heapify up במסגרתו השוונו הורה לילדיו והחלפנו ביניהם במידת הצורך. חזרנו על התהליך באופן רקורסיבי עד לקיום תכונות הערימה.

קוד הפייתון הבא מזין פריט חדש לערימה min-heap על ידי הכנסת הפריט למיקום השמאלי ביותר האפשרי של המערך (הערימה) ואח"כ ביצוע "heapify up" רקורסיבי שמחליף את הפריט עם ההורה הקטן ממנו כמה פעמים שצריך:

def heapify_up(arr, current_index):
    parent_index = (current_index - 1) // 2

    while current_index > 0 and arr[current_index] < arr[parent_index]:
        # Swap the current node with its parent
        arr[current_index], arr[parent_index] = arr[parent_index], arr[current_index]
        current_index = parent_index
        parent_index = (current_index - 1) // 2

def insert_min_heap(arr, item):
    # Add the new item at the end of the array (last position in the complete binary tree)
    arr.append(item)
    current_index = len(arr) - 1

    # Perform "heapify up" to maintain min-heap property
    heapify_up(arr, current_index)

# Example usage:
arr = [5, 7, 8, 9, 12, 10, 11]
insert_min_heap(arr, 6)
print(arr)

• הפונקציה insert_min_heap() מוסיפה פריט חדש item לערימת min-heap המיוצגת על ידי המערך arr. היא מצרפת את הפריט החדש אל סוף המערך ואז קוראת לפונקציה heapify_up() כדי לבצע את ההחלפות הנדרשות במטרה לקיים את תכונות ערימת min-heap.

אפשר לעשות heapify up גם כשמוסיפים פריט חדש לערימת min-heap וגם עבור max-heap. הפונקציה הבאה עושה heapify up גם לערימת מינימום וגם למקסימום תלוי בפרמטר שהיא מקבלת:

def heapify_up(arr, current_index, operation="min"):
    # Define the mapping of operation strings to comparison operators
    comparison_operators = {
        "min": lambda x, y: x < y,
        "max": lambda x, y: x > y
    }

    # Get the corresponding comparison operator based on the "operation" parameter
    compare = comparison_operators[operation]

    # Calculate the index of the parent node
    parent_index = (current_index - 1) // 2

    # Compare the current node with its parent and swap if needed
    # Continue this process until the current node reaches the root (index 0) or
    # it satisfies the heap property with respect to its parent
    while current_index > 0 and compare(arr[current_index], arr[parent_index]):
        # Swap the current node with its parent
        arr[current_index], arr[parent_index] = arr[parent_index], arr[current_index]

        # Update the current index to be the parent index for the next iteration
        current_index = parent_index

        # Recalculate the index of the new parent node for the next iteration
        parent_index = (current_index - 1) // 2

נסביר:

1. הפונקציה מקבלת שלושה פרמטרים: arr, המערך המייצג את הערימה; current_index, האינדקס של הפריט החדש שהוכנס שצריך לעבור למעלה בערימה; ו-operation, שמציין אם מדובר בערימת min או max (ברירת המחדל היא "min").
2. המילון comparison_operators מקשר את מחרוזת operation לפונקציית השוואה המתאימה. עבור ערימת min, פונקציית למדא x < y תבדוק אם x קטן מ-y. עבור ערימת max, פונקציית הלמדא x > y תבדוק אם x גדול מ-y.
3. המשתנה parent_index מחושב כ-(current_index - 1) // 2, שנותנת את מיקום הצומת ההורה בערימה. חישוב זה עובד בגלל ייצוג הערימה בעץ בינארי.
4. הלולאה while תמשיך לרוץ כל עוד current_index גדול מ-0 (כלומר, הצומת הנוכחי אינו השורש) ופונקציית compare תחזיר True (כלומר, הצומת הנוכחי מפר את תכונות הערימה ביחס להורה שלו).
5. בתוך הלולאה, אם תכונות הערימה מופרות, נחליף את הצומת הנוכחי עם ההורה שלו באמצעות טריק פייתוני: arr[current_index], arr[parent_index] = arr[parent_index], arr[current_index].
6. לאחר ההחלפה, מעדכנים את current_index להיות parent_index, ומחשבים מחדש את parent_index עבור האיטרציה הבאה.
7. הלולאה תמשיך לרוץ עד שה-current_index יגיע לשורש (אינדקס 0) או עד שהצומת הנוכחי יעמוד בתנאי הערימה ביחס להורה שלו.

פעולת heapify up חיונית לשמירת תכונות הערימה לאחר הכנסת פריט, והיא מבטיחה שהפריט החדש שהוכנס יועבר למעלה בערימה למיקום הנכון, תוך שמירה על מבנה הערימה והתכונות שלה.

קוד heapify ליצירת ערימה ממערך

בסעיף הקודם ראינו שכדי להוסיף פריט ל-heap צריך להוסיף אותו במיקום האחרון של המערך / העץ הבינארי ומשם לעשות לו heapify up. בסעיף זה נקבל מערך שלם ונבנה ממנו heap המקיים את תכונות הערימה על ידי כך שנעביר לתוך הערימה המתהווה את הפריטים אחד אחד על פי סדר שמיד נסביר מהו.

תהליך של סידור הפריטים בערימה כדי לשמור על תכונת הסדר של הערימה מכונה heapify. התהליך הוא רקורסיבי וכולל צעדים שבכל אחד מהם משווים הורה לילדיו ומחליפים, במידת הצורך.

קוד הפייתון הבא מקבל מערך ומחזיר ערימה heap מסודרת כ-max-heap או min-heap כתלות בפרמטר:

def heapify(arr=[], current_index=0, operation="min"):
    # Define the mapping of operation strings to comparison operators
    comparison_operators = {
        "min": lambda x, y: x < y,
        "max": lambda x, y: x > y
    }
    
    # Get the corresponding comparison operator
    compare = comparison_operators[operation]  

    # Initialize extreme (largest/smallest) as current parent
    extreme = current_index
    
    # Determine the left and right children of parent
    left_child_idx = 2 * current_index + 1
    right_child_idx = 2 * current_index + 2
    
    heap_size = len(arr)

    # If left child is larger/smaller than parent
    if left_child_idx < heap_size and compare(arr[left_child_idx], arr[extreme]):
        extreme = left_child_idx

    # If right child is extreme (largest/smallest)
    if right_child_idx < heap_size and compare(arr[right_child_idx], arr[extreme]):
        extreme = right_child_idx

    # If extreme is not root
    if extreme != current_index:
        # Swap
        arr[current_index], arr[extreme] = arr[extreme], arr[current_index]
        
        # Recursively heapify the affected sub-tree
        heapify(arr, extreme, operation)
        
def build_heap(arr=[], operation="min"):
    # Index of last non-leaf node
    start_idx = len(arr) // 2 - 1
 
    # Heapify all the nodes from the last non-leaf node to the 0th index leaf
    # Since the leaves have no children and so we don't need to heapify them
    for i in range(start_idx, -1, -1):
        heapify(arr, i, operation)

# Test case
arr = [2, 9, 7, 4, 5, 3, 6]
build_heap(arr, "max")
print(arr)

נסביר:

def build_heap(arr=[], operation="min"):
    # Index of last non-leaf node
    start_idx = len(arr) // 2 - 1
    # Heapify all the nodes from the last non-leaf node to the 0th index leaf
    # Since the leaves have no children and so we don't need to heapify them
    for i in range(start_idx, -1, -1):
        heapify(arr, i, operation)

• לולאת for רצה על הצמתים שאינם עלים בסדר הפוך ומעבירה לפונקציה build_heap() על מנת שפעולת ה-heapify up תתבצע על כל תת עץ מלמטה למעלה דבר המבטיח את הקניית הסדר הנכון לערימה heap כאשר מכניסים לתוכה פריטים חדשים.

מציאת ערך הקיצון של heap

או כיצד לעשות peek - לקבל מבלי למחוק - את הערך המקסימלי מ-max-heap ואת הערך המינימלי מ-min-heap

כדי לקבל את הערך המקסימלי מערימת מקסימום, אתה צריך לגשת לצומת השורש של הערימה. צומת השורש הוא תמיד הפריט המקסימלי בערימת מקסימום max-heap. באופן דומה, כדי לקבל את הערך המינימלי מערימת מינימום min-heap, ניגשים לצומת השורש, שהוא הפריט המינימלי בערימת מינימום.

בשני המקרים, השורש נמצא בעמדת האינדקס הראשונה של ייצוג המערך של הערימה arr[0].

הנה פונקציית Python לקבלת הערך המקסימלי או המינימלי של heap:

def peek(arr):
    if not arr:
        raise IndexError("Heap is empty")
    
    return arr[0]

# Example usage 1:
max_heap = [10, 9, 7, 4, 5, 3, 6, 2]
max_value = peek(max_heap)
print("Maximum value in max-heap:", max_value)

# Example usage 2:
min_heap = [2, 4, 5, 6, 7, 9, 10]
min_value = peek(min_heap)
print("Minimum value in min-heap:", min_value)

מחיקה של פריט ו-heapify down

כאשר מוחקים פריט מערימה delete, הפעולה הנפוצה ביותר היא להסיר את הפריט הקיצוני ביותר, שהוא השורש של הערימה. בערימת min-heap, השורש מכיל את הערך הקטן ביותר מבין כל הפריטים בערימה. כשמוחקים את השורש יש לשמור על תכונות הערימה, ולשם כך משתמשים ב-heapify down - תהליך המשווה בין ההורה לילדיו, ומחליף ביניהם אם צריך תוך תנועה מלמעלה למטה, מהשורש אל כיוון העלים.

תהליך מחיקת השורש ולאחריו heapify down כולל את השלבים הבאים:

1. מחליפים את השורש עם הפריט האחרון: כדי להסיר את צומת השורש, אנו מחליפים אותו עם הפריט האחרון של הערימה.

   

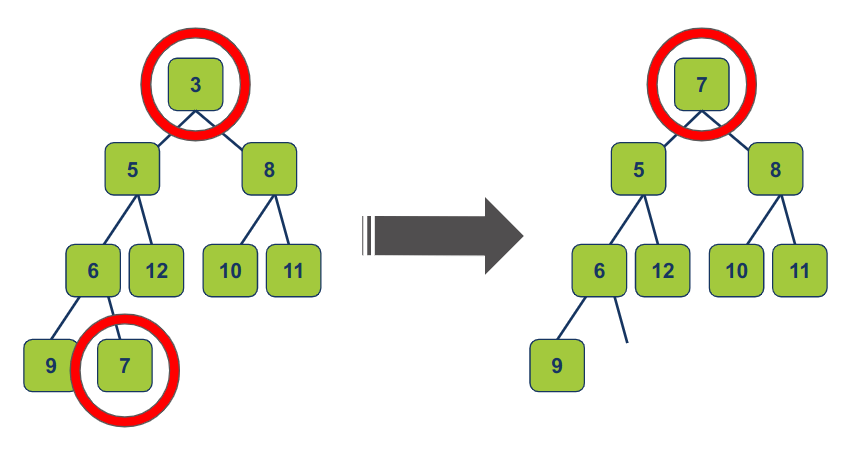
   • זה שומר על מבנה עץ בינארי מלא, מה שעלול לגרום להפרת תכונות הערימה כיוון שהשורש החדש עשוי להיות גדול יותר מהילדים שלו בערימת מינימום.

2. heapify down: כדי לשחזר את תכונות הערימה, אנו מבצעים פעולת "heapify down" החל מהשורש החדש (שהיה בעבר הפריט האחרון). בתהליך זה, אנו משווים את הצומת עם ילדיו ומחליפים אותו עם הילד הקטן ביותר בערימת min או הילד הגדול ביותר בערימת max עד שהוא מגיע למיקום הנכון או הופך לצומת עלה.

   

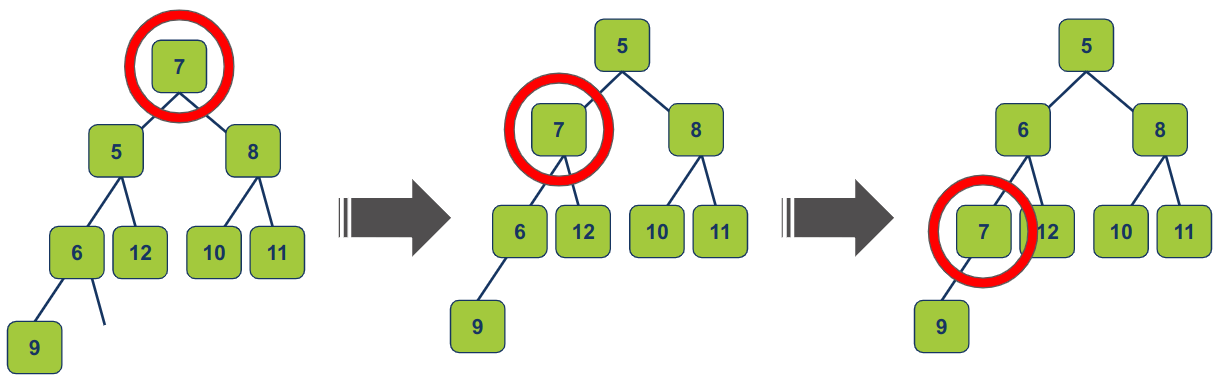
הפונקציה הבאה מוחקת את שורש הערימה ואח"כ עושה heapify down כדי לשחזר את תכונת הערימה:

def heapify_down(arr, current_index, heap_size, operation="min"):

    # Define the mapping of operation strings to comparison operators
    comparison_operators = {
        "min": lambda x, y: x < y,
        "max": lambda x, y: x > y
    }

    # Get the corresponding comparison operator based on the "operation" parameter
    compare = comparison_operators[operation]

    while True:
        left_child_idx = 2 * current_index + 1
        right_child_idx = 2 * current_index + 2

        extreme = current_index
        if left_child_idx < heap_size and compare(arr[left_child_idx], arr[extreme]):
            extreme = left_child_idx
        if right_child_idx < heap_size and compare(arr[right_child_idx], arr[extreme]):
            extreme = right_child_idx

        if extreme == current_index:
            # The current node is in its correct position, so we stop the heapify down process
            break

        # Swap the current node with the extreme child
        arr[current_index], arr[extreme] = arr[extreme], arr[current_index]

        # Move down to the extreme child and continue heapify down
        current_index = extreme

def delete_min_heap(arr):
    if not arr:
        raise IndexError("Heap is empty")

    # Swap the root (min element) with the last element
    arr[0], arr[-1] = arr[-1], arr[0]

    # Remove the last element (min element) from the heap
    min_value = arr.pop()

    # Perform heapify down starting from the root (index 0)
    heapify_down(arr, 0, len(arr), operation="min")

    return min_value

# Example usage:
min_heap = [3, 6, 8, 7, 12, 10, 11, 9]
min_element = delete_min_heap(min_heap)
print("Deleted element:", min_element)
print("Resulting min-heap:", min_heap)

סיבוכיות הזמן והמקום של פעולות נפוצות הנעשות על heap

סיבוכיות הזמן של הפעולות הנפוצות ביותר אותם ניתן לבצע על heap שיש בה n צמתים הן:

1. insert (הכנסה לערימה):

   • סיבוכיות זמן: O(log n)
   • הסבר: הכנסת פריט לערימה בינארית כרוך בהוספתו אל סוף הערימה ולאחר מכן ביצוע heapify up כדי לשמור על תכונות הערימה. פעולת "heapify up" יש לה סיבוכיות זמן של O(log n) מכיוון שהיא עוברת מהפריט שנוסף מעלה אל השורש, וגובהו המקסימלי של עץ בינארי מאוזן הינו log n.

2. delete (הסרה מהערימה):

   • סיבוכיות זמן: O(log n)
   • הסבר: הסרת פריט השורש בערימת min או max דורשת החלפתו עם הפריט האחרון, ולאחר מכן ביצוע heapify down כדי לשחזר את תכונות הערימה. פעולת "heapify down" יש לה סיבוכיות זמן של O(log n) מכיוון שהיא יורדת מהשורש אל העלים, כאשר המרחק שעליה לעבור הוא לכל היותר log n בערימה מאוזנת.

3. peek (מציאת-מינימום או מציאת-מקסימום):

   • סיבוכיות זמן: O(1)
   • הסבר: הפריט עם העדיפות הגבוהה ביותר נמצא תמיד בשורש הערימה. לכן, גישה לפריט עם העדיפות הגבוהה ביותר דורשת זמן ביצוע קבוע.

סיבוכיות מקום: O(n)

הסבר: סיבוכיות המקום של ערימה בינארית היא O(n) מכיוון שהיא מאחסנת n פריטים בייצוג מבוסס מערך. בערימה בינארית, הפריטים מסודרים בעץ בינארי מלא, וייצוג המערך מבטיח שכל רמה של העץ תהיה מלאה משמאל לימין.

נסכם. ערימה נחשבת למבנה נתונים יעיל לביצוע מספר פעולות נפוצות. דוגמת: הכנסה ומחיקה שתיהן דורשות לכל היותר זמן ביצוע O(log n), בעוד גישה לפריט שיש לו את העדיפות הגבוהה ביותר (peek) דורשת זמן ביצוע קבוע O(1). סיבוכיות המקום של ערימה בינארית היא O(n) בשל ייצוג בתוך מערך array המאכלס n פריטים. יעילות זמן הביצוע של פעולות הופכת את מבנה הנתונים ערימה heap לבחירה מתאימה ליישום תורי עדיפויות ויישומים נוספים להם נדרשת הכנסת פריטים יעילה ואחזור פריטים מבוסס עדיפות.

שימוש במודול heapq לצורך יישום ערימה בינארית ב-Python

ספריית heapq ב-Python מספקת פונקציות לעבודה עם ערימות בינאריות ביעילות.

להלן הדרכים שבהן תוכל להשתמש בספריית heapq לעבודה עם ערימות בינאריות:

1. יבוא המודול הפייתוני:

   ייבא את המודול heapq המצוייד במתודות לעבודה עם ערימות בינאריות.

   import heapq

2. יצירת ערימה מינימלית ממערך:

   כדי ליצור ערימת מינימום min-heap ממערך (לא בהכרח מסודר), השתמש במתודה heapify:

   data = [8, 3, 5, 2, 6, 8]
   heapq.heapify(data)
   print(data) # Output: [2, 3, 5, 8, 6, 8]

3. הסרת הפריט הקיצוני מהערימה:

   כדי להסיר (dequeue) את הפריט עם העדיפות הגבוהה ביותר (הערך הקטן ביותר בערימה מינימליות) יש להשתמש במתודה heappop.

   highest_priority_item = heapq.heappop(data)
   print(highest_priority_item) # Output: 2
   print(data) # Output: [3, 6, 5, 8, 8]

4. הוספת פריט לערימה:

   להוספת (enqueue) פריט לערימת המינימום, נשתמש במתודה heappush.

   heapq.heappush(data, 1)
   print(data) # Output: [1, 6, 3, 8, 8, 5]
   heapq.heappush(data, 7)
   print(data) # Output: [1, 6, 3, 8, 8, 5, 7]
   heapq.heappush(data, 9)
   print(data) # Output: [1, 6, 3, 8, 8, 5, 7, 9]

5. מיזוג 2 מערכים לערימה בינארית:

   כדי למזג שני מערכים ליצירת ערימה בינארית, יש להשתמש במתודה merge. שים לב שהתוצאה היא generator, אותו ניתן להמיר לרשימה.

   l1 = [8, 3, 5]
   l2 = [2, 6, 8]
   l3 = heapq.merge(l1, l2)
   print(list(l3)) # Output: [2, 6, 8, 3, 5, 8]

6. יצירת ערימת מקסימום max-heap:

   כדי ליצור ערימת מקסימום באמצעות heapq, תוכל להשתמש בפתרון לא הכי תקני על ידי שימוש במתודות _heapify_max ו-_heappop_max של הספרייה המיועדות להיות מתודות פרטיות ולא לשמש את המתכנתים, מה שאפשר להבין מהשימוש בקו תחתון לפני שם המתודות. לחלופין, תוכל ליצור את הקלאס שלך לצורך עבודה עם ערימת מקסימום.

   נעזר בספריית heapq ליצירת ערימת מקסימום:

   data = [8, 3, 5, 2, 6, 8]
   heapq._heapify_max(data)
   print(data) # Output: [8, 6, 8, 2, 3, 5]

   נסיר מערימת המקסימום את הפריט בעל הערך הגבוה ביותר:

   highest_priority_item = heapq._heappop_max(data)
   print(highest_priority_item) # Output: 8

   נוודא שהערימה שומרת על תכונות הערימה לאחר הסרת הפריט:

   print(data) # Output: [8, 6, 5, 2, 3]

   נוסיף פריט לערימה:

   heapq.heappush(data, 1)

   נוודא שהערימה שומרת על תכונות הערימה:

   print(data) # Output: [1, 6, 8, 2, 3, 5]

   • הסרת פריט מערימת מקסימום אינה גורמת להפרת תכונות הערימה לעומת זאת הוספת פריט לערימת מקסימום כשמשתמשים בספריית heapq גורמת להפרה.

   לפיכך, לאחר שהוספנו פריט לערימת מקסימום באמצעות heappush() אנחנו צריכים לסדר אותה:

   heapq._heapify_max(data)
   print(data) # Output: [8, 6, 5, 2, 3, 1]

יישום תור עדיפויות priority queue המבוסס על heap

מבנה נתונים heap משמש לעתים קרובות כדי ליישם תור עדיפויות priority queue ביעילות. תור עדיפויות הוא סוג נתונים מופשט המאפשר הכנסה ושליפה יעילות של פריטים על בסיס עדיפות שלהם. פריטים עם עדיפות גבוהה יותר נשלפים לפני פריטים עם עדיפות נמוכה יותר.

תור עדיפויות מספק את הפעולות הבאות עם סיבוכיות הזמן שלהן:

1. הכנסה insert (הכנסה לתור): הוספת פריט לתור עדיפויות עם עדיפות ספציפית.
2. מחיקה delete (הסרה מהתור): הסרת הפריט עם העדיפות הגבוהה ביותר מהתור.
3. peek: קבלת הפריט עם העדיפות הגבוהה ביותר מבלי להסיר אותו מתור העדיפות.

פעולות הללו יכולות להתבצע ביעילות באמצעות ערימה בינארית binary heap כפי שראינו בחלקים הקודמים של המדריך.

אתגר: משקל האבן האחרונה

נתון אוסף של אבנים, לכל אבן יש משקל שלם וחיובי.

בכל סיבוב, נטיח את שתי האבנים הכבדות ביותר מה שיגרום לריסוקם. נניח שלאבנים יש משקלים x ו- y עם x <= y. התוצאה של הטחה זו היא:

• אם x == y, שתי האבנים נהרסות לחלוטין.
• אם x < y, אבן במשקל x נהרסת לחלוטין, ולאבן במשקל y יהיה משקל חדש שווה ל- y - x.

בסוף, תיוותר אבן אחת לכל היותר. הפונקציה צריכה להחזיר את משקל האבן הזו (או 0 אם אין אבנים שנותרו).

כתוב פונקציה last_stone_weight(stones) שתקבל מערך אבנים ותחזיר את משקל האבן האחרונה.

חותמת הפונקציה:

def last_stone_weight(stones: [int]) -> int:
    # Your code here

לדוגמה:

stones = [2, 7, 4, 1, 8, 1]
last_stone_weight(stones)  # Output: 1

stones = [2, 7, 4, 1, 8, 1, 1]
last_stone_weight(stones)  # Output: 0

מגבלות:

משקל אבן חייב להיות מספר שלם הגדול מ-0.

רמז:

ניתן לפתור באמצעות priority queue.

הצעה לפתרון:

import heapq

def last_stone_weight(stones: [int]) -> int:
    # Heapify to max-heap since you want the heaviest stones to get precedence
    heapq._heapify_max(stones)
    
    # Keep smashing as long as you have at least 2 stones
    while len(stones) > 1:
        # Dequeue
        x = heapq._heappop_max(stones)
        y = heapq._heappop_max(stones)
        
        # Smash
        # Stone can't have a negative weight
        d = abs(x - y)
        
        # Stone can't have a 0 weight
        if d > 0:
            # Enqueue and heapify
            heapq.heappush(stones, d)
            heapq._heapify_max(stones)
    
    # Return the weight of the remaining stone or 0 if no stones left
    if len(stones) < 1:
        return 0
    elif len(stones) == 1:
        return stones[0]


# Test cases

stones = [2, 7, 4, 1, 8, 1]
print(last_stone_weight(stones))  # Output: 1

stones = [2, 7, 4, 1, 8, 1, 1]
print(last_stone_weight(stones))  # Output: 0

stones = []
print(last_stone_weight(stones))  # Output: 0

סיכום

במדריך זה, הסברנו מהי ערימה בינארית binary heap וכיצד להשתמש בה. ערימה היא מבנה עץ בינארי שלם המבטיח את תכונות הערימה. ערימות נחלקות לשני סוגים: ערימות מינימום min-heap, שבהן האב קטן יותר מהילדים שלו, וערימות מקסימום max-heap, שבהן האב גדול יותר. למדנו כיצד לייצג ערימות באמצעות מערכים, כיצד לבצע פעולות עריכה כדי לשמור על תכונותיהן, ועל טווח האינדקסים עבור צמתים פנימיים ועלים.

לאורך המדריך, הדגשנו את החשיבות של שמירה על תכונות הערימה בעת ביצוע פעולות הוספה ומחיקה, וסיפקנו דוגמאות קוד המיישמות עקרון זה.

הוספנו וחקרנו את ספריית heapq של פייתון המספקת מתודות לעבודה עם ערימות בינאריות, וכיסינו פעולות כמו הכנסה, הסרה, אחזור ומיזוג באמצעות הספרייה.

בנוסף, הסברנו את הנושא החשוב מאוד של תורי עדיפויות priority queues, שהם מבני נתונים המבוססים בד"כ על ערימות, ויישומם מאפשר הכנסה, אחזור, והסרה יעילים של פריטים על בסיס סדר קדימויות.

קריאת מדריך זה הקנת לך הבנה מוצקה של מבני הנתונים heap ו-priority queue, ושימוש בהם לצורך פתרון בעיות אלגוריתמיות.

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

יישום תורת הגרפים בפייתון - חלק א

יישום רשימת סמיכויות adjacency list - חלק ב בסדרה על גרפים

מיון טופולוגי באמצעות אלגוריתם Kahn

אלגוריתם חיפוש לעומק DFS - מהבנה ליישום

הבנת אלגוריתם חיפוש לרוחב - BFS - סריקה של גרפים ומציאת הנתיב הקצר ביותר

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים