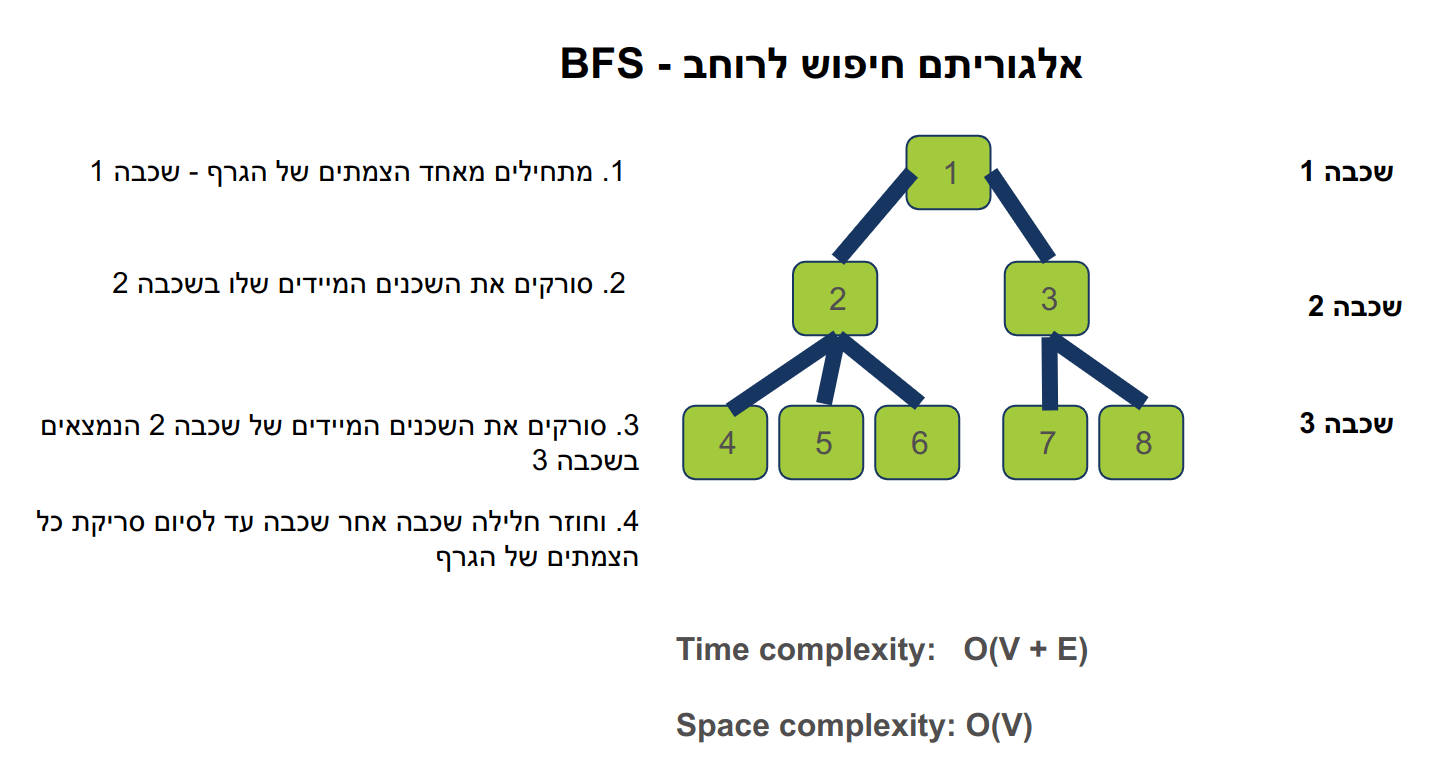
הבנת אלגוריתם חיפוש לרוחב - BFS - סריקה של גרפים ומציאת הנתיב הקצר ביותר

חיפוש לרוחב Breadth-first search (BFS) הוא אלגוריתם בסיסי לסריקת צמתים וקשׂתות של גרף באופן שיטתי ובשכבות. הוא מתחיל בצומת מסוים, חוקר את שכניו, ואז עובר לשכבת השכנים הבאה באמצעות מבנה נתונים של תור queue כדי לעקוב אחר סדר הסריקה. לחיפוש לרוחב יש סיבוכיות זמן של O(V + E) והוא שימושי במיוחד למציאת הנתיב הקצר ביותר בגרפים חסרי משקל וכן כבסיס לאלגוריתמים אחרים בתורת הגרפים.

סריקה של גרף, הידועה גם כמעבר, היא תהליך של ביקור ועיבוד של כל צומת בגרף. בגרף, צמתים מחוברים באמצעות קשתות, ו-BFS הוא אחד מאלגוריתמי הסריקה הבסיסיים המשמשים לחקר הצמתים והקשתות הללו.

חיפוש לרוחב (BFS) הוא אלגוריתם סריקה בסיסי של גרפים. הוא נמצא בשימוש נרחב לחקר גרפים והוא שימושי במיוחד למציאת הנתיב הקצר ביותר בגרפים חסרי משקל. בניגוד לאלגוריתמים אחרים המשמשים לסריקת גרפים, BFS סוקר את הצמתים בשכבות, כלומר הוא מתחיל בצומת מסוים וחוקר את כל שכניו לפני שהוא עובר לשכבת השכנים הבאה.

סיבוכיות הזמן של BFS היא O (V + E), כאשר V הוא מספר הצמתים (קודקודים) של הגרף, ו-E הוא מספר הקשתות. במונחים פשוטים, הזמן הדרוש לביצוע BFS גדל באופן לינארי עם מספר הצמתים והקשתות בגרף.

כאשר סורקים בעזרת BFS, האלגוריתם מתחיל בצומת נתון (צומת המקור) וחוקר את שכניו המיידיים. לאחר ביקור כל השכנים של הצומת הנוכחי, הוא עובר לסרוק את השכנים של אותם שכנים בשכבה הבאה. תהליך זה נמשך עד שכל הצמתים אליהם ניתן להגיע מצומת המקור נסרקו בשכבות של סריקה.

כדי לסרוק גרף שכבה אחר שכבה BFS נשתמש במבנה נתונים תור queue. תור עוקב אחר עקרון First-In-First-Out (FIFO), בדומה לתור המתנה בעולם האמיתי. לדוגמה במסעדה. אלגוריתם BFS שומר תור של צמתים שצריך לבקר בהם בעתיד. בתחילה, התור מכיל רק את צומת המקור. ככל שהאלגוריתם מתקדם, הוא מוציא צמתים מהחלק הקדמי של התור ומכניס את השכנים שלהם, שהוא טרם סרק, אל חלקו האחורי של התור.

אלגוריתם לביצוע חיפוש לרוחב BFS

שלבי אלגוריתם BFS:

• האלגוריתם מתחיל לרוץ מצומת מסוים אותו מכניסים לתור queue ומסמנים כמי שנסרק.
• בזמן שהתור אינו ריק, מסירים את הצומת הקדמי מהתור ומעבדים אותו.
• סורקים את השכנים של הצומת הנוכחי.
• אם שכן טרם נסרק, אז מוסיפים אותו לתור.

קוד הפייתון הבא מיישם חיפוש לרוחב BFS. הוא סורק את הגרף בשכבות כשהוא מבטיח כי הצמתים נחקרו בסדר שבו הם הועברו לתור בזכות השימוש במבנה נתונים Queue תור. ההערות המשולבות בגוף הפונקציה מסבירות את יישום האלגוריתם באמצעות הפונקציה bfs():

from collections import deque

def bfs(graph, start):
    # Create an empty set to keep track of visited nodes
    visited = set()   
    # Create a deque and enqueue the starting node          
    queue = deque([start]) 
    # Mark the starting node as visited     
    visited.add(start)          

    # Start the BFS loop, continue until the queue is empty
    while queue:     
        # Dequeue the front node from the queue           
        current_node = queue.popleft()  
        
        # Process the node (you can modify this based on your needs)     
        print(current_node, end=", ")                 

        # Explore neighbors of the current node
        for neighbor in graph[current_node]: 
            # Check if the neighbor has not been visited yet
            if neighbor not in visited:  
                # Mark the neighbor as visited   
                visited.add(neighbor)    
                # Enqueue the neighbor to the queue for further exploration  
                queue.append(neighbor)

נסביר:

1. מבני נתונים:

   • הקוד משתמש ב-deque מהמודול collections כדי ליישם את מבנה הנתונים של התור. deque הוא בחירה יעילה ליישום תור ב-Python בגלל ביצועים משופרים כאשר התור ארוך.
   • הסט visited משמש למעקב אחר הצמתים שכבר ביקרו בהם כדי להימנע מביקורים חוזרים באותו הצומת.

2. אתחול:

   • הפונקציה מאתחלת סט ריק visited, המחזיק את הצמתים אותם סרקה הפונקציה, ו-queue המכיל, בשלב ראשון, את הצומת start אשר מהווה את נקודת המוצא של הסריקה. בשורה הבאה, הצומת start נוסף לסט visited.

3. לולאה:

   • לולאת while ממשיכה לרוץ כל עוד יש צמתים ב-queue. בכל מחזור של הלולאה, מוסר הצומת הקדמי מן ה-queue (באמצעות המתודה popleft()). בצומת זה אפשר לעשות מה שדורשת המשימה שעל הפרק אבל במקרה זה, הוא פשוט מודפס.

4. סריקת השכנים:

   • עבור כל שכן של הצומת current_node (שנלקח מה-graph[current_node]), הקוד בודק אם השכן לא נסרק עדיין (כלומר, לא נמצא בקבוצת ה-visited). אם הצומת עוד לא נסרק, הקוד מסמן אותו כ-visited ומוסיף ל-queue לצורך סריקה בהמשך.

יישום זה של BFS הוא דרך קצרה ויעילה לביצוע האלגוריתם ב-Python, והוא אמור לעבוד היטב לסריקת גרפים. אם יש לך דרישות ספציפיות או פונקציונליות נוספת שאתה רוצה להוסיף, אתה יכול לשנות את הקוד בהתאם.

נבדוק את הפונקציה ליישום אלגוריתם חיפוש לרוחב BFS:

# Sample graph represented as an adjacency list
sample_graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}


# Test 1: Starting BFS from node 'A'
print("Test 1 - BFS starting from 'A':")
bfs(sample_graph, 'A')
# Expected output: A, B, C, D, E, F


# Test 2: Starting BFS from node 'D'
print("Test 2 - BFS starting from 'D':")
bfs(sample_graph, 'D')
# Expected output: D, B, A, E, F, C


# Test 3: Starting BFS from node 'F'
print("Test 3 - BFS starting from 'F':")
bfs(sample_graph, 'F')
# Expected output: F, C, E, A, B, D

סיבוכיות זמן ומקום של אלגוריתם BFS:

סיבוכיות זמן:

סיבוכיות הזמן של אלגוריתם BFS היא O(V + E), כאשר V הוא מספר הצמתים (הקודקודים) בגרף, ו-E הוא מספר הקשתות. וביתר פירוט:

• ביקור בכל צומת פעם אחת: הלולאה while תמשיך עד שהתור יתרוקן. במקרה הגרוע ביותר, היא תעבור על כל הצמתים בגרף פעם אחת, וזה O(V).
• סריקת השכנים: בכל פעם שהלולאה while רצה, האלגוריתם סורק את השכנים של הצומת הנוכחי. מספר הקשתות הכולל בגרף הוא E. סריקת כל השכנים דורשת O(E) פעולות במקרה הגרוע ביותר.
• נשלב את שני הרכיבים, ונקבל שסיבוכיות הזמן הכוללת היא O(V + E).

סיבוכיות מקום:

סיבוכיות המקום של אלגוריתם BFS היא O(V), כאשר V הוא מספר הצמתים (הקודקודים) בגרף. שטח זה משמש לאחסון סט ה-visited והתור.

• הסט visited: מאחסן מידע על צמתים שנסרקו. במקרה הגרוע ביותר, הוא עשוי להכיל את כל הצמתים בגרף, וכתוצאה מכך סיבוכיות המקום שלו היא O(V).
• תור: מבנה הנתונים queue מאחסן צמתים אותם יש לסרוק במהלך BFS. במקרה הגרוע ביותר, הוא עשוי להכיל את כל הצמתים בגרף. לפיכך, דרושה לו סיבוכיות מקום של O(V).
• מכיוון שהשטח בזיכרון המשמש את הסט visited והתור שניהם דורשים סיבוכיות מקום O(V) סיבוכיות המקום הכוללת גם היא O(V).

לסיכום, לאלגוריתם BFS יש סיבוכיות זמן של O(V + E) וסיבוכיות מקום של O(V), מה שהופך אותו ליעיל לצורך סריקת גרפים.

אתגר: מציאת הנתיב הקצר

תיאור האתגר התכנותי:

נתון גרף לא ממושקל המיוצג באמצעות רשימת סמיכויות. המשימה שלך היא למצוא את הנתיב הקצר ביותר בין הצמתים start ו-end.

אתה יכול להיעזר בתבנית הבאה לצורך כתיבת הפתרון:

def shortest_path(graph, start, end):
  """
  Finds the shortest path between the start and end nodes in the given graph.
  Args:
    graph: The graph represented as an adjacency list.
    start: The start node.
    end: The end node.

  Returns:
    The shortest path between the start and end nodes.
  """

  # TODO: Implement this function.

  pass

דוגמה לבדיקה:

graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}

start_node = 'A'
end_node = 'F'

result = shortest_path(graph, start_node, end_node)
print(result)  # Output: ['A', 'C', 'F']

הפונקציה shortest_path() להלן מיישמת את אלגוריתם החיפוש לרוחב (BFS) כדי למצוא את הנתיב הקצר ביותר בין שני צמתים בגרף לא ממושקל המיוצג באמצעות רשימת סמיכויות adjacency list:

from collections import deque

def shortest_path(graph, start, end):
    # Set to keep track of visited nodes
    visited = set()
    visited.add(start)
    
    # Queue to perform BFS, starting with the (node, path) tuple
    q = deque()
    q.append((start, [start]))
    
    while q:
        # Dequeue the front node and its path
        current_node, current_path = q.popleft()
        # If the current_node is the 'end' node
        if current_node == end:
            # Return the shortest path from start to end
            return current_path
        
        # Explore neighbors of the current node
        for neighbor in graph[current_node]:
            # Check if the neighbor is not visited yet
            if neighbor not in visited:
                # Mark the neighbor as visited
                visited.add(neighbor)
                # Extend the path with the neighbor.
                # Works even if `path` is None
                new_path = current_path + [neighbor]
                # Enqueue the neighbor with the updated path
                q.append((neighbor, new_path))
    
    # If no path is found
    return []

נעבור על הפונקציה ונבין כיצד היא מיישמת את אלגוריתם BFS שלב אחר שלב:

1. הפונקציה מקבלת שלושה פרמטרים:

   • graph: רשימת סמיכויות המצייגת גרף.
   • start: צומת המקור ממנה מתחילה סריקת BFS.
   • end: צומת היעד

   תפקידה של הפונקציה למצוא את הנתיב הקצר ביותר מ-start ל- end.

2. אתחול:

   • הפונקציה מאתחלת סט visited כדי לעקוב אחר הצמתים שנסרקו.
   • הצומת start מתווסף לקבוצה visited דבר המהווה אינדיקציה לכך שהוא נסרק.
   • היא גם יוצרת מבנה נתונים "תור" לו קראנו q לסידור הצמתים שיש לסרוק. התור מכיל בתחילה את הזוג (start, [start]), המייצג את הצומת ההתחלתי ואת הנתיב מהצמת ההתחלתי אל עצמו.

3. ביצוע BFS בתוך לולאת while:

   • החלק העיקרי של הפונקציה הוא לולאת while שממשיכה לרוץ עד שהתור מתרוקן. לולאה זו מבצעת את סריקת BFS של הגרף.
   • בכל פעם שהלולאה רצה, הצומת הקדמי והנתיב שלו מוסרים מהתור באמצעות q.popleft(). הצומת הקדמי מייצג את הצומת הנוכחי שנסרק, והנתיב הוא הנתיב מהצומת start אל הצומת הנוכחי.
   • אם הצומת הנוכחי current_node הוא צומת המטרה אז הפונקציה מחזירה את הנתיב הנוכחי current_path שהוא בהכרח הנתיב הקצר ביותר כיוון שהאלגוריתם BFS סורק במעגלים הולכים ומתרחקים מצומת ההתחלה.
   • הפונקציה אז סורקת את השכנים של הצומת הנוכחי current_node בתוך לולאת for כאשר רשימת השכנים מתקבלת מ- graph[current_node].
   • עבור כל שכן של current_node, הפונקציה בודקת אם השכן לא נסרק עדיין. אם השכן לא נסרק, הוא מסומן כמי שנסרק על ידי הוספה לסט visited.
   • הפונקציה מרחיבה את הנתיב הנוכחי על ידי הוספת השכן אליו, ויוצרת נתיב חדש שנקרא new_path.
   • הפונקציה מוסיפה את השכן ואת new_path שנוצר מהוספתו ל-current_path כצמד אל התור queue לסריקה באיטרציה הבאה.

4. הערך המוחזר:

   • אם הסריקה מסתיימת מבלי למצוא נתיב אל צומת היעד, הפונקציה מחזירה רשימה ריקה [] כדי לאותת על כך שאין נתיב מ-start אל end.

המקרים הבאים ישמשו לבחינת הפונקציה:

# Adjacency list representation of a graph
graph = {
1: {2, 5},
2: {1, 3, 5},
3: {2, 4},
4: {3, 5, 6},
5: {1, 2, 4},
6: {4},
7: {7}
}


# Trivial cases
print(shortest_path(graph, 1, 2))


print(shortest_path(graph, 1, 1))


# Longer paths
print(shortest_path(graph, 1, 4))


print(shortest_path(graph, 1, 6))


# No path
print(shortest_path(graph, 1, 7))


# No node
print(shortest_path(graph, 2, 8))




# Try with another input type
graph = {
'A': ['B', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F'],
'D': ['B'],
'E': ['B', 'F'],
'F': ['C', 'E']
}


start_node = 'A'
end_node = 'F'


result = shortest_path(graph, start_node, end_node)
print(result) # Output: ['A', 'C', 'F']

סיכום

BFS הוא ראשי תיבות של Breadth-First Search, או חיפוש לרוחב הינו אלגוריתם יעיל לסריקת גרף באופן שיטתי, תחילה הוא בודק את כל הצמתים המחוברים לצומת נתון, ואז את כל הצמתים המחוברים לצמתים אלה, וכן הלאה. ל-BFS ישנם כמה שימושים שהבולט בהם הוא למציאת הנתיב הקצר ביותר בין שני צמתים בגרף.

BFS הוא אלגוריתם פשוט יחסית ליישום, אך הוא יכול להיות יעיל מאוד עבור גרפים גדולים. הוא נחשב לאחד האלגוריתמים החשובים ביותר בתורת הגרפים, ומשמש בסיס של רבים אחרים.

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

יישום תורת הגרפים בפייתון - חלק א

יישום רשימת סמיכויות adjacency list - חלק ב בסדרה על גרפים

Pyviz - ספרייה להצגת גרפים אינטראקטיביים

מיון טופולוגי באמצעות אלגוריתם Kahn

תורים Queues - הבנה ויישום בפייתון

General Tree data structure עץ נתונים

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים